计及FACTS校正的N-k故障约束鲁棒机组组合

石志伟

(山东理工大学计算机科学与技术学院，山东 淄博255000)

0 引言

考虑预想故障的调度方法是保障电力系统安全运行的重要调度方法[1]。该调度方法在经济调度时考虑了电力系统可能出现的运行故障，能够保障电力系统在预想故障下的安全运行。传统的N-1预想线路故障集合，能够保证系统在任意一条线路断线的情况下安全运行[2]。由于输电线路直接暴露在天气中，容易受到恶劣环境的影响，其故障概率较高，此外，随着电力系统规模的不断扩大，很有可能存在多条线路同时发生故障的情况[3]。因此系统的运行需要从传统的N-1线路预想故障演化为N-k线路预想故障集。因此，本文将针对输电线路的N-k故障展开研究。

如果将所有的N-k故障作为预想故障集考虑，那么模型规模将远超N-1故障的调度方法，难以求解。因此缩小N-k故障集合的规模成为研究重点。文献[4]引入效用理论来获取并缩小N-k故障集合。文献[5]提出基于影响增量的N-k故障分析法，能够筛选出电网的高影响N-k故障状态。在缩小N-k计算规模的同时，为保证电网在所有N-k故障下均能安全运行，部分文献采用了鲁棒优化[6-9]。文献[6]基于两阶段鲁棒，提出了考虑N-k故障的鲁棒机组组合模型。该模型在第一阶段(日前)制定机组启停计划，机组出力则在第二阶段(次日日内)制定，并保证得到的机组启停计划能够应对所有的N-k预想故障。文献[7]提出了考虑输电线路结构优化的N-k故障鲁棒机组组合，并指出在日前优化输电结构能有效缓解次日N-k故障下的系统切负荷。文献[8]提出了气电联合系统的N-k故障约束机组组合模型。文献[9]考虑N-k预想故障集的电力系统规划方法。具有min max-min形式的两阶段鲁棒优化能快速有效寻找最严重的N-k故障，并保证系统的调度方案在所有N-k故障下均可行[10]。

FACTS设备能够调节线路参数，从而控制故障后的潮流，在保证系统安全运行的同时提升系统运行经济性。目前考虑FACTS的运行优化领域已有较多研究成果。文献[11]指出FACTS能缓解N-1故障下的线路过载。文献[12-13]提出考虑FACTS的最优潮流，并采用遗传算法等方法求解该模型。文献[14-15]提出考虑FACTS的安全约束最优潮流。然而上述文献均采用智能算法进行求解，其结果最优性无法保证。文献[16-18]提出了混合整数线性规划(mixed integer linear programming，MILP)形式的含FACTS设备的直流最优潮流。该模型引入0-1整数变量与大M法表征装有FACTS线路的潮流方向。通过求解该MILP模型，其结果的最优性能有效得到保证。虽然目前关于考虑FACTS的电力系统调度方法已有了很多研究成果，但尚无文献考虑其在N-k故障约束调度方法中的应用。

基于上述分析，本文提出了考虑FACTS校正控制的N-k故障约束鲁棒机组组合，以保证电力系统在N-k故障下安全运行同时提升其运行经济性。该方法在鲁棒优化的第一阶段(日前)制定机组启停计划，在第二阶段(日内)制定FACTS与机组出力计划。FACTS设备在不同故障场景下出力不同。本文提出基于嵌套式列生成(nested column-and-constraint generation，Nested C&CG)的双层分解算法以求解此两阶段鲁棒问题，其中上层算法将原问题分解为机组计划制定主问题与最严重场景运行子问题，下层算法用于求解子问题，以寻找最严重场景。

1 模型描述

1.1 FACTS等效模型与所提调度方法

图1给出了考虑FACTS后线路的示意图。与文献[16-18]一样，本文的FACTS设备仅指UPFC与TCSC。该类型FACTS装置可通过改变串接在输电线路中的电容器组或直接改变线路潮流，来提高线路输送能力。本文将FACTS装置的调节作用均等效为对线路参数的改变，FACTS作为可变电抗加入到线路中。在考虑FACTS后，线路的电抗可视为变量。

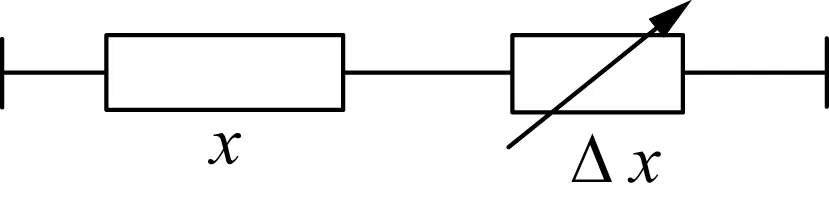
图1 考虑FACTS设备的等效电路图

图2给出了本文的调度方法。机组启停计划是在日前就已经制定，在次日不可更改。启停计划鲁棒性必须保证，该计划要能够应对所有可能出现的N-k预想故障。在次日日内调度中，每个预想故障会有对应的机组与FACTS出力。不同的预想故障下机组出力与FACTS出力是不同的。

图2 所提调度方法

1.2 具体模型

为方便讨论分析，本文仅考虑线路的N-k预想故障。线路发生N-k故障时，会影响其他线路的潮流分布，可能会导致部分线路潮流出现越限。采用0-1整数变量Jl,t描述线路的状态，1表示线路处于正常运行状态，0表示线路处于故障状态，系统的N-k不确定性集合Φ可用式(1)描述[19]。

(1)

式中：R为输电线路状态集合；l为所有线路集合；Γt为鲁棒调节系数，表示在t时刻系统最多停运线路的数量，该系数取值与k相同。Jl,t≥Jl,t+1限制线路的状态。如果在t时刻线路停运，那么假设在接下来的调度时段，线路状态都处于停运状态。

本文选取文献[6-7]所提的N-k鲁棒机组组合框架。模型的目标函数包括机组的启停费用，机组最小运行费用与系统在最严重场景下的运行费用，如式(2)所示。本文关注在FACTS已经规划的情况下，如何充分利用FACTS设备的灵活性以在保证电力系统在N-k故障下的安全经济运行。如果研究FACTS设备的规划，那么在目标函数中需要考虑FACTS设备的投入成本。通常而言，机组总运行成本包括机组运行费用(消耗燃料的费用)与机组启动与停机成本。由于本文对机组运行费用进行了分段线性化处理，因此机组运行费用被分为了两个部分[6-7]：最小运行费用与增量运行费用。最小运行费用是指考虑机组最小出力约束下，启动机组运行在最小出力值的运行成本(消耗燃料的费用)。增量运行费用则是指当机组出力高于其最小出力的时候，增加的出力消耗的燃料费用。

(2)

(3)

式中：PGi,t,p为t时刻第i个机组的第p分段的有功出力；ci,p为第i个机组在第p分段的燃料系数；η为切负荷惩罚系数；Dj,t为负荷节点j在t时刻的切负荷值。

1.2.1 机组组合约束

1)机组启停费用

(4)

式中：CUi和CDi为机组开、停机费用；ui,t和vi,t为表征机组启动和关闭的0-1整数变量，需要满足：

(5)

ui,t+vi,t≤1 ∀i,∀t

(6)

2)最小启停时间约束。

(7)

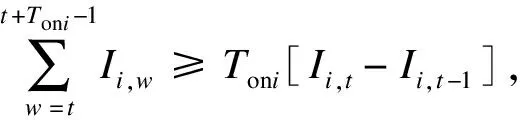
∀t∈[Loni+1,T-Toni+1]

(8)

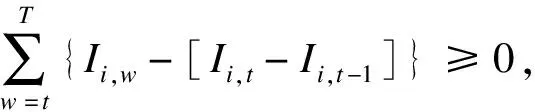
∀t∈[T-Toni+2,T]

(9)

(10)

∀t∈[Loffi+1,T-Toffi+1]

(11)

∀t∈[T-Toffi+2,T]

(12)

式中：Ii,w机组i在w时刻的运行状态；w为当前运行时刻；T为总调度时间；Toni和Toffi分别为最小的连续开机、停机时间；Loni和Loffi分别为最初所需持续开机时段和停机时段时间，满足Loni=min{T,[Toni-Toni,0]Ii,0}，其中Toni,0为机组初始时刻的开机时间，Ii,0为机组i的初始运行状态，Loffi=min{[Toffi-Toffi,0][1-Ii,0]}，其中Toffi,0为机组初始时刻的关机时间。

1.2.2 系统运行约束

1)基尔霍夫第一定律

(13)

式中：下标b为节点参数，表征节点b；Kb,l、Gb,i、Cb,j为对应的参数；Fl,t为线路l在t时刻的潮流大小；PBj,t为负荷节点j在t时刻的负荷值；PGi,t为机组i在t时刻的有功功率出力。

2)机组出力约束

(14)

(15)

式中：Pmini为机组i的最小有功功率出力值；Pmaxi,p为机组i第p分段的最大有功功率出力。

机组爬坡约束：

(16)

式中：Rupi和Rdni分别为第i台机组每小时上/下爬坡的最大值；Supi和Sdni分别为第i台机组开机/停机时的爬坡约束。

3)线路容量约束

-Jl,tFmaxl≤Fl,t≤Jl,tFmaxl∀l,∀t

(17)

式中：Fl,t为线路l在t时刻的潮流值；Fmaxl为线路l的潮流正常容许最大值。

对于未安装FACTS设备的线路，其潮流与节点相角的关系为：

|FL,t-(θsL,t-θeL,t)/xL|≤M1(1-JL,t)∀L,∀t

(18)

式中：FL,t为未安装FACTS线路L在t时刻的潮流值；θsL,t和θeL,t为未安装FACTS线路L的开始与结束节点在t时刻的相角值；下标sL和eL为线路L的首端与尾端节点；M1为一个极大的正数。

对于安装FACTS设备的线路，由于其电抗变成变量，其潮流与节点相角的关系为非线性约束。采用文献[16-18]所提的大M法将其转换为线性约束，该约束可写为：

(19)

(20)

2 求解方法

基于上述分析，本节提出基于Nested C&CG[20]的双层分解循环算法以求解该问题。其中上层算法将原问题分解为机组启停主问题与最严重场景运行子问题，下层算法通过迭代求解该max-min子问题，以寻找最严重场景。

先将原问题写成式(21)所示简写形式。

(21)

式中：N为第一阶段决定的0-1整数变量，包括机组状态变量I与机组启停变量u、v；P、J、h为第二阶段决定的连续变量；Y为第二阶段决定的0-1整数变量，包括线路潮流的方向y为阶中的连续变量；g(J)为随机场景；AT、BT、C、D、Q、H均为常系数矩阵。式(21)中第一类约束代表原问题中的约束式(4)—(12)；第二类约束代表原问题中的约束(13)—(20)。

2.1 上层循环

上层循环将原两阶段问题分解为主问题与子问题。主问题用于获取机组启停计划，需要加入子问题产生的最严重场景。其步骤如下。

1)设置主问题上界Uout=+∞，主问题下界Lout=-∞，初始迭代m=0，求解主问题式(22)(定义为MP)，得到N的值N*，更新下界Lout=η。

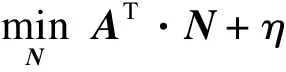
s.t.C·N≤h

η≥0,N∈{0,1}

(22)

式中：η为引入的变量，是对子问题目标函数的估计，同时也是子问题目标函数的下界；

2)令m=m+1。将N*带入子问题中，调用下层循环算法求解子问题，获取第m次迭代时的最严重场景gm(J*)，并更新上界Uout。

3)如果上下界差值不满足判据式(23)，向主问题加入对应的约束式(24)；如果满足判据式(23)，那么终止循环，输出机组启停方案。

|Uout-Lout|≤ε

(23)

(24)

式中：ε为一个很小的正数；Pm、Ym分别为在第m次迭代中加入的连续变量。

2.2 下层循环

下层循环是负责迭代求解子问题，以获得最严重的场景，从而返回至主问题。子问题模型如下：

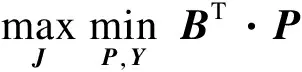
s.t.D·N*+Q·Y+H·P≤g(J)

P≥0,Y∈{0,1}

(25)

由于式(25)中的min问题中含有0-1整数变量Y，因此该问题不能采用强对偶理论转对偶。如果将该整数变量赋予一个初值，那么该问题就是一个线性优化问题，可以用强对偶理论转对偶求解。具体求解步骤如下。

1)设定优化问题式(25)的上下界分别为Uin=+∞，Lin=-∞。设定初始迭代系数h=1；赋予0-1变量Y一个初值Yh*。采用强对偶理论将其转换单层问题，并调用列生成算法，可得上界子问题式(26)(定义为UBSP)。该问题的最优解是式(25)的上界。求解式(26)，更新上界Uin=τ，并得到场景gm(J*)。

s.t.τ≤(g(J)-D·N*-Q·Yh*)Tλh

HT·λh=B,τ≥0

(26)

式中：τ为对目标函数式(26)的预估值；Yh*为第h次迭代时整数变量Yh的初值；λh为第h次迭代时建立的对偶变量。

2)将得到的场景g(J*)带入到下界子问题式(26)(定义为LBSP)中，检验该场景是否为最严重场景，求解LBSP，更新下界Lin=max{Lin,BTP*}。

s.t.D·N*+Q·Y+H·P≤g(J*)

P≥0,Y∈{0,1}

(27)

3)如果上下界差值不满足判据式(28)，那么该场景不是最严重场景。令h=h+1；将LBSP得到的整数变量值Yh*带入式(29)，并将式(29)加入到UBSP中；创造新的变量λh，重新开始下层循环的步骤1)。如果满足判据，那么说明g(J*)是最严重场景。终止循环，将得到的该场景返回到MP中，并令Uout=Uin。

|Uin-Lin|≤ε

(28)

(29)

式(29)含有双线性变量g(J)λh，难以直接求解；由于本文的不确定场景集为线路故障，不确定变量为J，因此该模型中的双线性变量实质上是Jλh，是0-1整数变量与连续变量相乘，因此可引入大M法[20]写成混合整数线性形式，如式(30)所示。

(30)

式中：φ为引入的中间变量；M2为一个极大的正数。

2.3 求解步骤

综上所述，本文所提模型的求解算法流程图如图3所示。

图3 求解算法流程图

3 算例

节将所提模型与算法测试于6节点系统与修正的IEEE RTS-79系统。定义不考虑FACTS与N-k故障的机组组合为UC。定义考虑FACTS，但不考虑N-k故障的机组组合为UC-F。定义不考虑FACTS，考虑N-k故障的机组组合为CUC。所提模型为CUC-F。

3.1 6节点算例

本节将所提模型测试于6节点系统，该系统包括6个节点，3台机组，11条线路。本文采用文献[21]提出的方法确定FACTS安装线路，分别安装于线路2、5、6、7。FACTS的容量为30%，即该线路的电抗可以在原有电抗基础值的70%～130%变化，其拓扑结构可如图4所示。由于6节点是一个较小的系统，仅用来阐述所提模型的有效性，因此该算例中的N-k准则取N-1。

图4 6节点系统拓扑图

表1给出了不同调度方法下的系统运行费用。由表1可知，UC-F的费用比UC低。这是因为FACTS设备能够更改线路参数，改善系统的潮流分布，从而降低了调度费用。由于UC与UC-F均未考虑N-k预想故障，虽然其费用较低，但是在故障发生后可能会出现潮流越限等后果，给系统运行带来风险。CUC考虑了N-k预想故障，该调度方法具有较好的鲁棒性，能够保证系统故障后安全运行。但是该调度方法在故障后出现了切负荷，因此其总费用最高。由于FACTS设备能够在故障发生后改善潮流分布，CUC-F的费用低于CUC。同样，该方法考虑了N-k预想故障，所以机组启停计划的鲁棒性得到了保障。CUC-F能够在保证系统调度方案鲁棒性的同时，降低系统的运行费用。

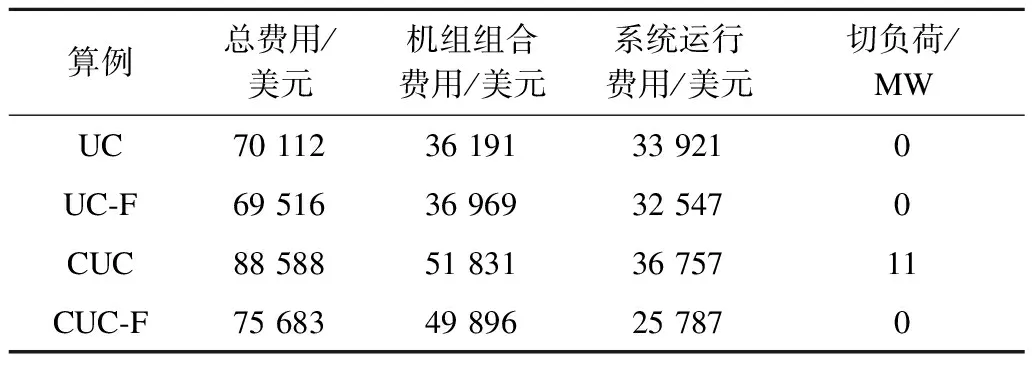
表1 不同算例下的费用分配

表2给出了第10 h下不同模型下的线路2潮流值。假设线路容量值为1 p.u.。假设线路1发生故障。由于UC-F和UC未考虑N-k预想故障，因此在线路1发生故障之后，该线路潮流越限，从而威胁了电力系统的安全运行。CUC和CUC-F均考虑了预想故障，因此它们故障后的潮流均未发生越限，系统的安全运行得到了保证。由于CUC-F中考虑了FACTS设备，系统在N-k故障下的校正能力得到了加强。因此CUC-F在故障前能允许线路以更高的潮流值运行，从而提升了系统的经济性。

表2 不同模型下线路2的潮流值

表3给出了第10 h下，所提CUC-F模型在不同N-k故障下的各个FACTS设备的出力值。由于篇幅原因，表3仅对6条线路故障进行分析。如果线路2发生故障，线路2上的FACTS设备不再调节线路电抗。线路5、6、7线路的电抗分别变为其基准值的119.8%(100%+19.8%)、70%(1-30%)、70%。可以看到，不同的预想故障下，大部分FACTS设备的出力值也会变化以缓解线路的潮流越限。

表3 CUC-F中不同N-1故障下FACTS的出力

3.2 修正的IEEE RTS-79节点系统

本节将所提模型测试于IEEE RTS-79节点系统，该系统包括24个节点，33台机组，38条线路。为了避免N-k预想故障造成大量的节点孤岛，算例将原系统中的输电线路都进行双倍处理，即系统的线路变更为76条。该算例中的N-k准则取N-2，拓扑结构可如图5所示。本节设计了下述3个算例。

图5 RTS- 79节点系统拓扑图

算例Ⅰ：系统安装4个FACTS设备，分别位于线路5、6、24、39。

算例Ⅱ：系统安装7个FACTS设备，分别位于线路5、7、24、29、39、62、65。

算例Ⅲ：系统安装10个FACTS设备，分别位于线路1、5、6、24、27、39、44、62、65、67。

4 算例分析

表4给出了所有算例中CUC与CUC-F的启动机组数量。假设FACTS设备的容量均为0.7。因为CUC中不考虑FACTS设备，因此算例I、Ⅱ、Ⅲ中的机组组合情况是相同的。由表4可知，在引入了FACTS设备后，系统的灵活性与故障的校正能力得到了提升，系统不再需要启动额外的机组以保证系统在故障下的安全运行，因此CUC-F在4 h、5 h等时刻的启动机组数少于CUC。同理，随着FACTS设备数量的上升，系统的灵活性得到加强，因此算例Ⅲ在4 h、5 h等时刻的启动机组数小于算例 I与算例 Ⅱ。

表4 不同算例下的每小时机组启动数量

图6给出了不同算例下系统的总费用随着FACTS容量的变化。由图6可知，系统的总费用随着FACTS的容量增大而降低。当FACTS安装数量与算例Ⅰ一致时，由于此时FACTS安装数量较少，FACTS容量的上升对系统的灵活性提升有限，即使FACTS容量上升至0.9 p.u.，其运行费用仍然较高。当FACTS安装位置与算例Ⅱ、Ⅲ一致时，系统的运行费用随着FACTS容量的上升显著下降。当FACTS安装位置与算例Ⅲ一致，容量为0.9 p.u.时，系统的总费用降低了12%。

图6 系统运行费用随FACTS容量的变化曲线

表5给出了不同N-k准则下CUC-F调度方法的运行费用。其中FACTS安装位置与算例Ⅲ一致，FACTS容量为0.7 p.u.。由表5可知，随着k的值上升，系统的运行费用与最大启动机组数量也随之增加。系统需要启动额外的机组以保证系统的安全运行。由于RTS-79系统本身安全性较高，因此在N-1时并未出现切负荷。当k>1时，系统需要在N-k故障下切除负荷以保证系统安全。

表5 不同N-k准则下的调度费用

5 结语

本文提出了计及FACTS校正控制的N-k故障约束鲁棒机组组合模型。FACTS设备用于缓解线路故障后的潮流越限。本文进一步提出了基于Nested C&CG的分解算法求解所提的鲁棒机组组合模型。将所提模型与算法测试于6节点系统与IEEE RTS-79系统。结果表明FACTS的引入能有效提升电力系统灵活性，能够保证系统在N-k预想故障下安全，并提升其经济性。所提算法能够将原3层优化问题分解为主子单层问题求解，并且能有效寻找到最严重场景，从而保证调度方案的鲁棒性。