液滴撞击液面形成的液坑形态特征及其重力势能分析

郭 通，袁德奎，赵丰泽

天津大学 机械工程学院力学系，天津 300350

0 引 言

液滴撞击液面是自然界和工业领域常见的现象。在重力、表面张力、压力和黏性力等多种因素的作用下，液滴撞击液面的过程中会出现飞溅、液冠形成、液坑扩张与收缩、次生液柱生成、液柱破碎为次生液滴以及液滴漂浮等复杂而有趣的现象。

1876年，Worthington 等[1-2]记录了不同下落高度、不同直径的水银与牛奶撞击玻璃后的液滴铺展形状，以瞬时摄影技术拍摄了水滴撞击水与牛奶混合溶液以及牛奶液滴撞击水面的运动过程。此后，研究者对液滴撞击液面问题进行了持续研究，试图描绘其完整图像，并揭示其规律和内在机理。蔡一坤[3]观察到液滴撞击液面过程中的“穿入”“劈裂”和“飞溅”三种现象，总结出发生液滴“穿入”现象的下落高度经验公式，以及飞溅过程中坑径、坑深、形成最大凹坑所需时间、中心柱回弹时间与下落高度的关系。郑哲敏[4]对蔡一坤的实验过程和数据进行了分析，指出“环形穿入”现象是由液滴脱离管口后的自由振动造成的。Rein[5]的研究表明：由于初始速度等条件不同，液滴撞击液面过程中会出现液滴漂浮、反弹、合并和飞溅等现象；在液滴与目标液体合并过程中，液体内部会出现涡环，而在飞溅过程中目标液体内会形成液坑、液冠、液柱等多种形态。Bisighini等[6]通过实验研究了液坑无量纲深度和无量纲宽度随时间的变化过程，从理论上推导出了液坑最大无量纲深度。Ouz 等[7]采用边界单元法对液滴撞击液面过程进行了数值模拟研究，发现在液坑底部会出现气泡卷吸现象。Vander Wal[8]等通过实验研究了不同液膜厚度（液膜厚度与液滴直径之比为0.1～10.0）对液滴撞击液面效果的影响，发现薄液膜促进飞溅、厚液膜抑制飞溅。Manzello 和Yang[9]对水滴撞击水池和C4F9OCH3（HFE7100）溶液池（液池深度2～25 mm）分别进行了实验，发现韦伯数越大，水滴撞击液面后形成的液柱越高，且液柱发生破碎的临界韦伯数与液池深度相关（韦伯数范围为5.5～206.0）。Castillo-Orozco 等[10]通过实验研究了液体黏性、表面张力、撞击速度对液滴撞击液面后运动形态的影响，发现撞击速度越大，产生的中心液柱越高，液柱越容易破碎生成次生液滴，并且给出了液坑深度和中心液柱高度随时间的变化曲线。夏秀文等[11]建立了液滴撞击液面对冲聚合模型，得出了碰撞过程中抛射液滴的反弹速度以及总能量损耗率；但为简化模型忽略了被撞击液面的流体特性，因此实验中的液滴反弹速度比理论结果小。马慧敏等[12]在液滴撞击液面实验中发现：液坑最大深度和最大水平长度、液柱最大高度随韦伯数增大呈线性增大；韦伯数越大，液坑和液柱的形态变化越快，液坑和中心液柱持续时间越长，液柱达到最大高度及生成次生液滴的时刻也越晚。曹刚等[13]发现液滴撞击成泡是概率性问题，受液滴撞击速度、液池深度、回落二次液滴等影响，液滴撞击浅液池可以形成一个圆泡，撞击深液池可以先形成环形泡再演变为1～2 个圆泡。裴传康等[14-15]通过数值模拟对微小水滴撞击深液池过程进行了研究，发现液坑形状有U 形和半球形两种，且一般分别向V 形和圆柱形转变。郑明飞[16]通过二维数值模型研究了双液滴同时撞击液膜（厚5 mm）的过程，发现双液滴会互相影响，撞击区域外侧射流，发展形成皇冠状水花，中心射流势能最终转化为外侧水花发展能量。Michon 等[17]发现：不同弗劳德数下，液滴撞击液面生成液柱的速度和粗细不同，且表面波传播和液坑收缩均会影响液柱的形成。Liang 等[18]使用Level Set 耦合VOF 的方法对液滴撞击液膜过程进行了数值模拟，结果表明：液冠直径随无量纲液膜厚度的减小而增大，与韦伯数和雷诺数无关；液冠高度随韦伯数增大而增大，与雷诺数关系不大。Saha 等[19]结合高速激光诱导荧光和阴影图技术对液滴撞击液池后形成的涡环形态演变进行了实验研究，发现涡环运动可分为线性、非单调和减速运动三个阶段，在运动过程中惯性、毛细和黏性效应交替起主导作用。

除运动形态及规律外，液滴撞击液面过程中的能量转化也是研究者关注的重要问题。Engel[20]对撞击中形成的液泡进行简化，假设液滴撞击能量一半传递到液池的重力势能和表面能，忽略其他较小能量，推导出液坑深度表达式，与实验结果符合良好。Macklin 等[21]建立了液滴撞击深液池和极浅液池两种情况的简化几何模型，提出了液坑达到最大深度时的表面能、重力势能以及黏性耗散能量方程式，推导出达到最深液坑时的液坑深度和液柱高度的表达式，研究发现：韦伯数越大，被撞击液体接收的初始液滴能量越小，且越接近初始液滴能量的一半，这与Engel 等提出的假设一致。马慧敏等[22]用VOF方法模拟液滴撞击过程，发现撞击过程中动能、表面能和重力势能相互转化，液滴初始速度越大，能量损耗越大。Hasegawa 等[23]的研究表明：液坑体积受液滴直径与撞击速度影响；对于水滴，液柱体积随撞击速度增大而增大，对于乙醇液滴，更高的撞击速度和更大的液滴直径会增大液柱体积；无论液体属性如何，约28%的撞击能量用于液坑形成，其余能量极可能消散或消耗于表面。Xu 等[24]对不同环境温度（20～78 ℃）下的水滴撞击乙醇溶液后达到最大液坑和最高液柱时的能量转化问题进行了研究，发现初始液滴能量的44.1%～74.5%转化为液坑最大时的重力势能和表面能，液坑最大时重力势能和表面能的31.1%～71.8%转化为液柱最高时的重力势能和表面能，且能量传递比随温度升高呈线性增大。

此外，研究者还对液滴撞击冷却着火液体（如油池）[25-26]、壁面[27]等液滴撞击应用问题开展了相关研究。

液滴撞击液面问题已经取得了丰硕的研究成果，但其关注的重点多是液体本身属性（如表面张力、黏性等）对其形态变化的影响，而鲜见液池深度对撞击过程的影响研究。因此，本文尝试通过实验探究液池深度、液滴直径对液滴撞击液面过程的影响，希望进一步加深对液滴撞击液面过程的认识。

1 实验装置及方法

实验装置如图1所示。用于产生液滴的针头固定于高度可调节的金属支架上。为调节液滴直径，实验采用了3 种规格的针头（23G、19G、14G）。针头后以导管连接蠕流泵，用于控制产生液滴的大小和时间间隔。针头正下方放置一个透明玻璃水箱，其中液体深度可根据实验要求调节。水箱一侧架设一部高速相机（NAC Memrecam HX-6，镜头焦距50 cm，分辨率2560 像素×1920 像素，采样频率1000 帧/s）。在与镜头相对的水箱另一侧设置300 W 的LED 光源，以保证高速拍摄所需的光强。相机连接至电脑，将实验采集的数据实时传输至电脑并以图片形式存储。

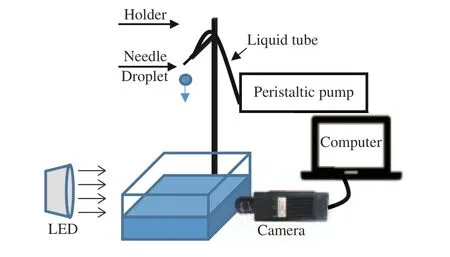
图1 实验装置示意图Fig.1 Experimental set-up

实验液体为纯净水，密度998.8 kg/m3，表面张力系数73.19 mN/m，动力黏性系数1.081×10–3Pa·s。环境和水的温度保持为17 ℃，气压为大气压。

液滴直径及撞击初速度（液滴刚接触液面时的速度）是两个关键实验参数。通过针头直径和蠕流泵可以调节液滴直径，但无法直接确定液滴直径。实际上，在表面张力作用下，针头滴出的液滴明显比针头直径更大。因此，需要先行对照片中液滴进行数字化处理，获得以像素为单位的液滴直径，然后乘以预先标定好的系数，得到实际的液滴直径。撞击初速度则是通过液滴刚接触液面时连续两帧照片上液滴的位移与间隔时间（1 ms）的比值进行计算。

已有研究表明，由初始液滴参数定义的韦伯数We是影响整个撞击过程的重要无量纲数：

式中，ρ和σ为水的密度和表面张力系数，d和v为液滴直径和撞击速度。

为考察撞击速度v、液滴直径d和液池深度h0对液滴撞击液面过程的影响，实验中设置8 个不同下落高度（400、510、640、790、940、1110、1300 和1500 mm），在每个高度下设置5 种不同的h0，在每种h0下设置3 种不同的液滴直径，共计120 组实验方案。每组方案重复实验3 次，共计360 组次实验。表1列出了实验方案及相应参数（范围）。

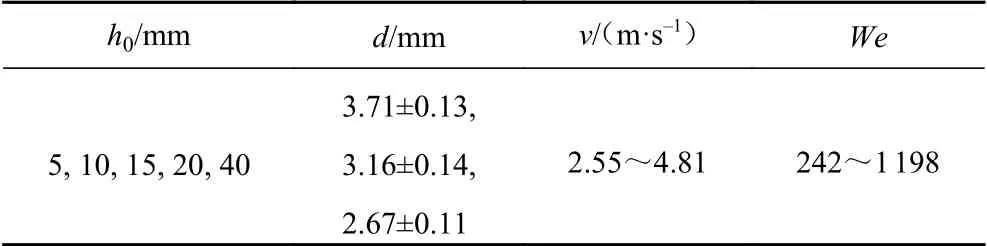
表1 实验方案及相应参数Table 1 Experimental scheme and parameters

2 实验现象

观测和分析120 组实验所得图像（视频），发现对于液池较深和液池较浅两种情况，液滴撞击液面后的运动形态明显表现出不同的特性。下面对这两种情况分别进行阐述。

在本文中，当液坑能够充分扩张和收缩时，认为液池较深。实验中，h0为40、20 和15 mm 的全部实验组次以及h0为10 mm 的部分组次，液坑均能充分发展。图2以h0=40 mm 为例给出了液池较深情况下液滴撞击液面后运动形态随时间的变化过程。液滴刚接触液面时，在1～2 ms 内会向外推挤出一圈薄膜，随后薄膜破碎成一圈小液滴。之后，液面出现凹坑并迅速扩大。当液坑达到最大体积时，剖面呈半椭圆形，同时液坑开始收缩。液坑收缩并非各向均匀，由四周向内收缩的速度明显低于由下向上收缩的速度，因此液坑形状变得更瘪。一般情况下，若液滴初始动能足够大，液坑收缩过程中就会生成一个液柱。液柱向上运动至一定高度后开始落回液面。液柱在内部速度差和表面张力影响下会产生次生液滴（通常1～2 个；后文次生液滴均指液柱顶部分离出的液滴）。在液柱几乎达到最高点时，次生液滴基本成形（图2中114 ms 时的图像）；而在液柱落回液面过程中，次生液滴逐渐与液柱分离（在图2中，139 ms 时已完全分离）。次生液滴成形后，随液柱一起向下运动、落回液面，使已基本恢复平静的液面再次被撞击出较小的液坑。

图2 液滴撞击深液池后的运动过程（d =3.71 mm，v =4.81 m/s，h0=40 mm）Fig.2 Process of droplet impact on deep liquid pool (d =3.71 mm，v =4.81 m/s，h0=40 mm)

在h0=5 mm 的全部实验组次以及h0=10 mm 的部分组次中，液坑受液池底部影响明显，不能充分发展。图3给出了液池较浅情况下撞击后运动形态随时间的变化过程。液滴接触液面后的1～2 ms 内，会向四周溅出一圈小液滴，这与液池较深的情况相同。当液坑生成并开始扩大时，其运动形态与液池较深的情况差异显著：受底部限制，液坑在深度方向不能继续扩大，只能向四周扩张，液坑形状近似一个横切掉底部的半球；液坑体积达到最大时，开始收缩，由四周向内收缩的速度明显低于由下向上收缩的速度，液坑变为圆锥形；收缩过程同样会产生液柱，且液柱运动过程中也会产生次生液滴；与液池较深的情况相比，液柱上升速度更快，液柱更细。此外，在液池较深的情况下，次生液滴没有明显的向上速度；而在液池较浅的情况下，次生液滴从上升速度更快的液柱分离后，会向上运动一段距离后才落回液面，且数量更多。对比图3（a）和（b）可以看出，h0=10 mm时产生的次生液滴数目（9 个）比h0=5 mm 时更多，这可能是因为液滴撞击更浅的液池时，液池底部的影响更为显著，运动形态更为混乱，更多能量被耗散，导致可用于推动液坑扩张和收缩的动能减少。

图3 液滴撞击浅液池后的运动过程Fig.3 Process of droplet impact on shallow liquid pool

3 实验结果分析

从上节实验现象可知，由于液池底部的作用，在液坑、液柱和次生液滴等的发展过程和形态方面，液滴撞击较浅液池与较深液池的情况差异显著。作为液滴撞击较浅液池问题的初步探索，后文重点讨论此情况下的液坑形态特征及其与We的关系，并尝试对液坑发展过程中的能量转化规律进行分析。

3.1 液坑形态特征分析

图4给出了液坑相关特征几何量的定义。L为液坑最大水平长度，即液坑体积最大时的水平长度。H为液坑最大深度：当液坑不触底时（完整液坑），H对应于液坑体积最大时的垂直深度；当液坑触底时（非完整液坑），H为液池深度h0。RC为液坑最大半径，即液坑体积最大时的半径。

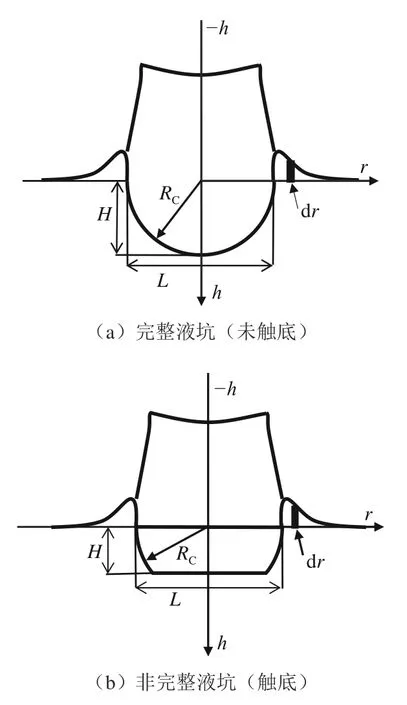
图4 液坑形状示意图Fig.4 Schematic diagram of crater shape

对于液池较深、液坑未接触液池底部的情况（完整液坑），液坑近似半球状。图5（a）给出了本文实验中完整液坑L和H的关系。可以看出，L和H基本呈线性关系，H/L的平均值约为0.65。图5（b）给出了非完整液坑L和H的关系，可明显看出：液池较浅时，由于底部限制，H只能达到h0；但液坑沿水平方向依然能够扩展，h0相同时，L随d增大而增大。

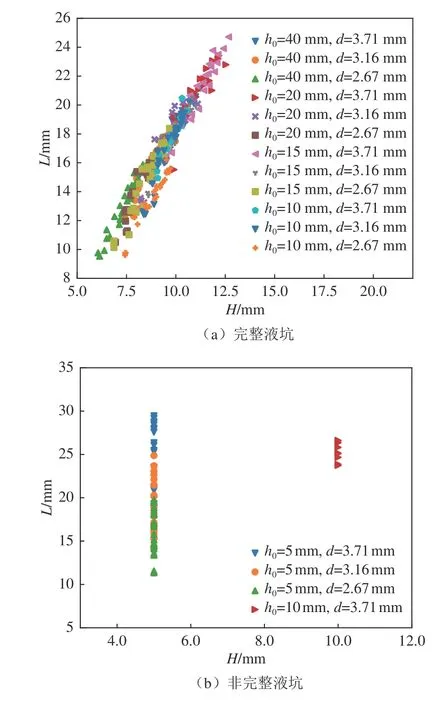
图5 L 与H 的关系Fig.5 Relationship between L and H

3.2 液坑最大水平长度L、最大深度H 与We的关系

已有研究表明，对于液池较深的情况（完整液坑），液滴撞击液池后的运动形态与基于液滴参数定义的We（见式（1））密切相关[12]。对于液池较浅的情况（非完整液坑），We、d和h0的作用尚不明确。下文对不同We（由d和v确定）下、不同h0的液池中的L和H变化规律进行分析。

图6和7 分别给出了液池较深时完整液坑的无量纲最大水平长度L/d和无量纲最大深度H/d与We之间的关系。可以看出：1）L/d和H/d均随We增大而增大，且在We较小时增大较快，而当We较大时，L/d和H/d的增大趋势变缓；2）在We和h0相同的情况下，L/d和H/d随初始液滴直径d的增大而减小，如图6（a）～（d）和图7（a）～（d）所示；3）在We和d相同的情况下，当h0从40 mm 减小至15 mm 时，L/d和H/d均增大，但当h0从15 mm 减小至10 mm 时，L/d和H/d反而减小，如图6（e）～（g）和图7（e）～（g）所示。

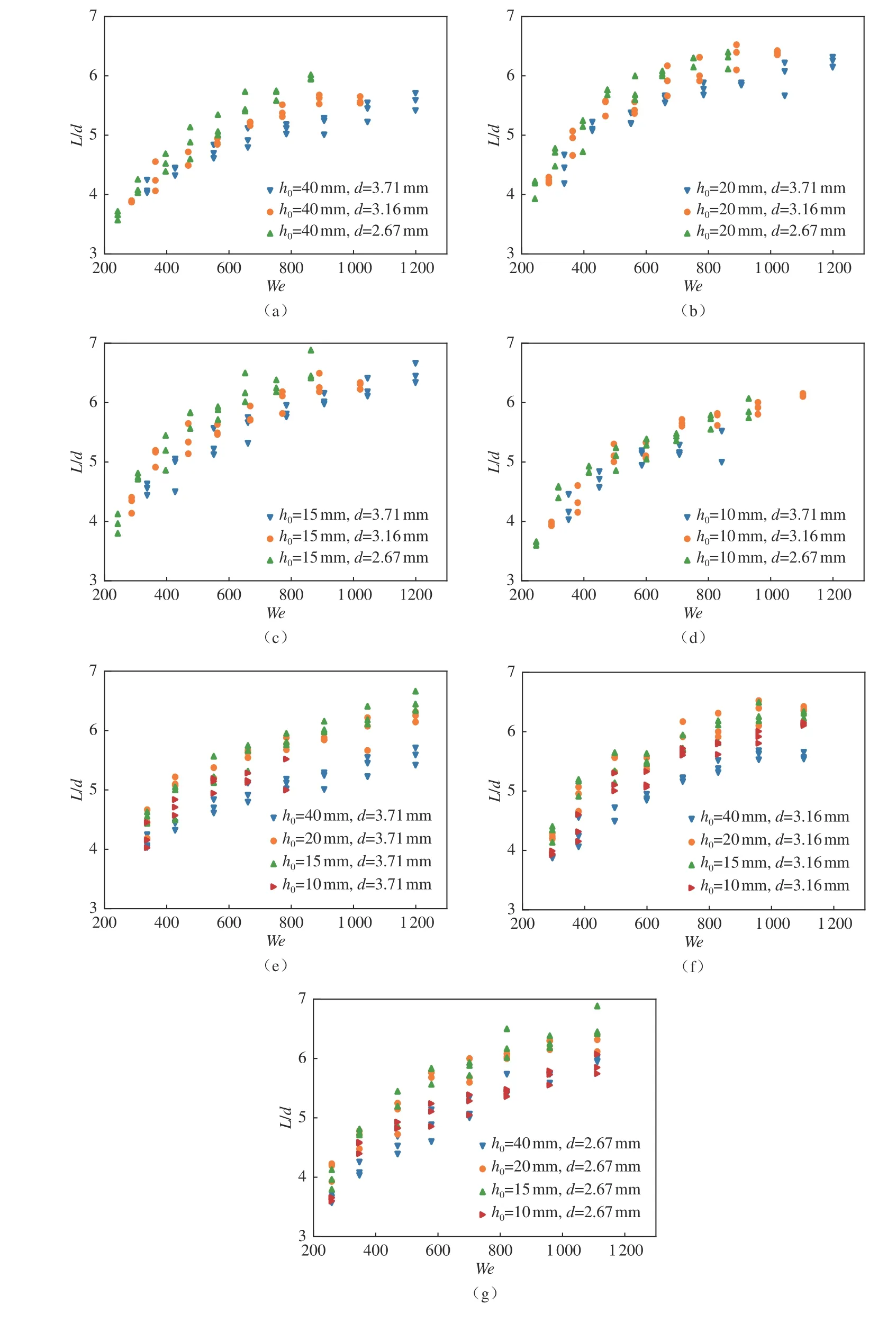
图6 完整液坑L/d 与We 的关系（a～d：不同液滴直径；e～g：不同液池深度）Fig.6 Relationship between L/d and We for complete crater (a-d:different droplet diameters；e-g:different pool depths)

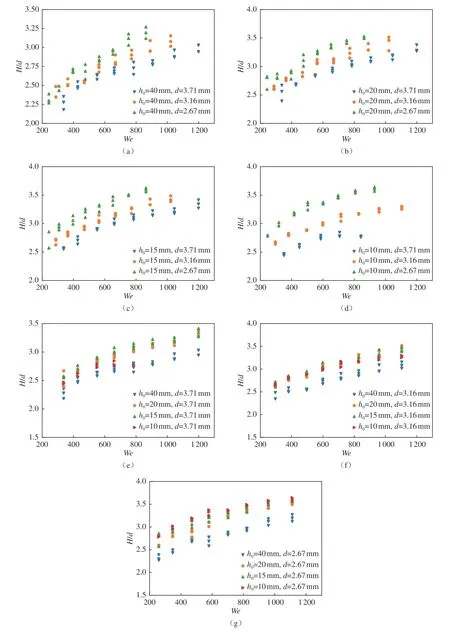
图7 完整液坑H/d 与We 的关系（a～d：液滴直径对比；e～g：液池深度对比）Fig.7 Relationship between H/d and We for complete crater (a-d:different droplet diameters；e-g:different pool depths)

对于非完整液坑，图8显示L/d随We增大而增大，这与完整液坑情况下的变化趋势是一致的。受实验条件限制，本研究仅在h0为5 和10 mm 的部分实验组次中捕捉到非完整液坑，但从图8（a）可以看出，当We和h0都相同、We小于约640 时，L/d随d增大而减小，但当We大于800 以后这一趋势不复存在。从图8（b）可以看出，当We和d都相同时，L/d依然随h0增大而减小，与完整液坑情况下的变化趋势一致。对于非完整液坑的情况，由于液坑已经触底，故其H与h0一致。总体来看，对于非完整液坑，虽然液池底部限制了液坑在深度方向的发展，但其在水平方向依然能自由发展，故L/d随We、d和h0的变化趋势与完整液坑基本一致。但是，当h0相同而We较大时，L/d随d的变化规律与完整液坑显著不同。

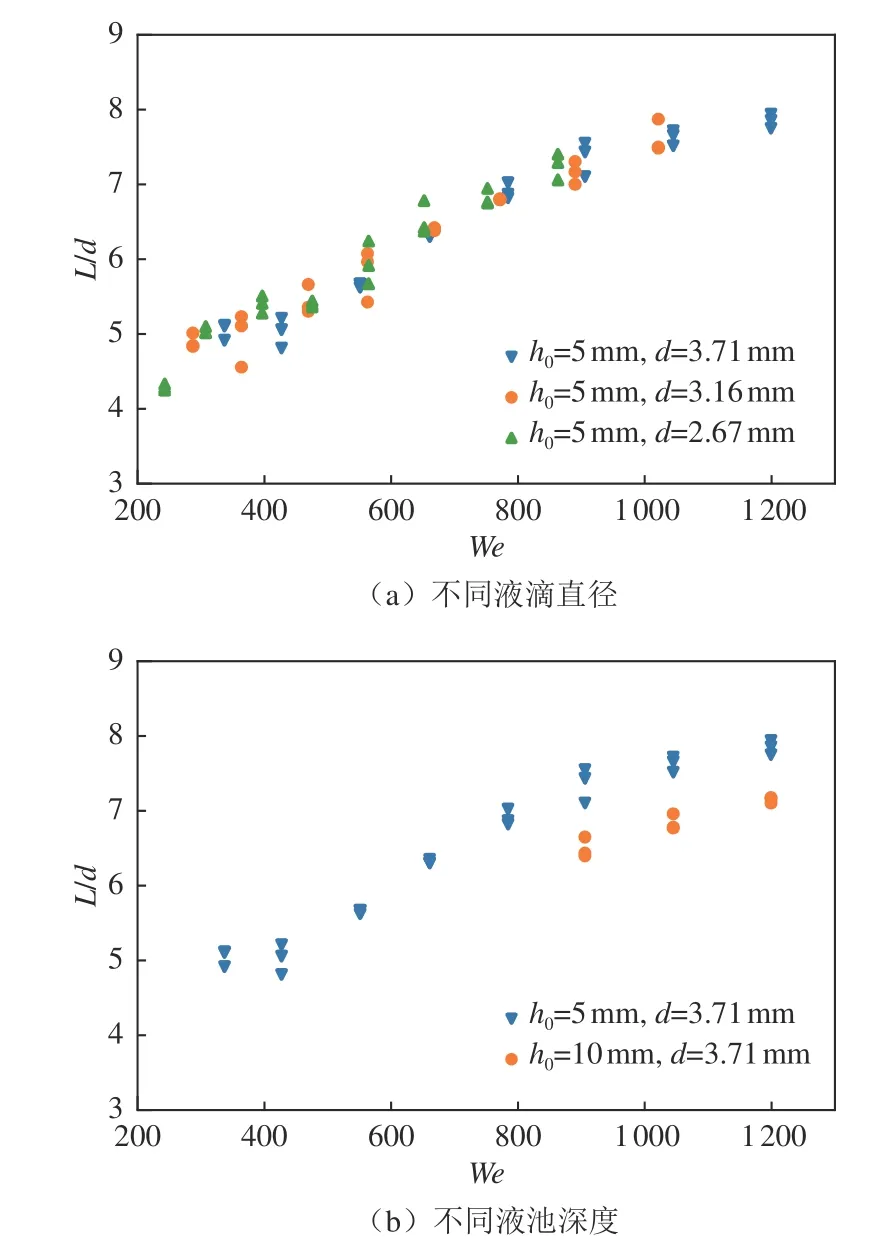
图8 非完整液坑L/d 与We 的关系Fig.8 Relationship between L/d and We for incomplete crater

以上分析表明：在液池深度h0较深（40、20 和15 mm）、We相同的情况下，对于完整液坑，H/d和L/d均随d增大而减小；对于非完整液坑，当We小于640 时L/d也大致体现出这一规律。下面从能量转化角度定性分析产生这一规律的原因。首先将无量纲液坑最大深度表达为如下形式：

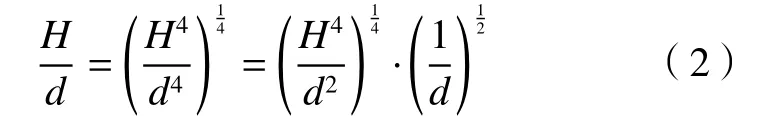
液滴接触液池表面瞬间的初始动能E可表示为：

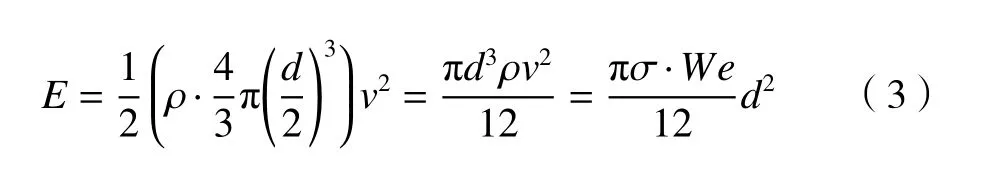
从式（3）可知，We相同时，液滴初始动能和液滴直径的平方d2成正比。假设当液坑达到最大时，液滴初始动能按一定比例转化为液坑重力势能[23]，再考虑到液坑重力势能与H4成正比，则在We不变时，H4与d2成正比。

由式（2）可知，H/d随d增大而减小。完整液坑达到最大时接近半球形，故H与L之比约为1/2，因此L/d也随d增大而减小。液池较浅（10 和5 mm）时，即使液坑没有触底，受底部影响，液体运动更加剧烈，液滴撞击损失能量更多，导致重力势能占液滴初始动能的比例也有所减少，L/d和H/d的变化与液池较深的情况差异显著。下面将通过估算定量分析液坑重力势能。

3.3 液坑重力势能分析

液滴撞击液面后，液坑形成及发展过程伴随着重力势能、动能、表面能及热能等多种能量形式之间的转化；这些能量转化过程对于液滴撞击液面后产生的各种复杂现象有着重要影响，得到了广泛关注和持续研究。已有研究表明，在完整液坑的发展过程中，液坑重力势能和表面能是撞击后液滴初始动能的能量转化过程中的重要组成部分[20-24]。根据马慧敏等[22]的数值模拟结果，重力势能和表面能量级相当：从撞击开始，重力势能和表面能逐渐增大；液坑最大时，重力势能和表面能都达到峰值；随着液坑收缩，重力势能和表面能开始降低。根据Hasegawa等[23]的研究成果，约28%的撞击能量转化为最大液坑的重力势能。基于相关成果，本文重点定量分析液坑重力势能，并尝试将其推广至非完整液坑的情况。

3.3.1 完整液坑（液坑未触底）

液滴和液池中液体组成的系统总能量等于液滴撞击液面时的初始动能E，由液滴直径和速度决定，如式（3）所示。液坑从产生至体积最大的过程中，系统动能逐渐减小，重力势能和表面能逐渐增大。液坑体积达到最大时，令系统重力势能为U。根据Engel[20]的几何模型，液坑可分为3 个部分：液面以下的液坑、液面上围成一圈的冠部以及冠部之上的一层很薄的液膜，如图4（a）所示。忽略液膜体积以及撞击时飞溅的液滴体积，根据质量守恒定律可知，冠部体积与液坑体积相等。根据实验观察到的现象，液坑近似为半球形，则液坑的重力势能U1为：

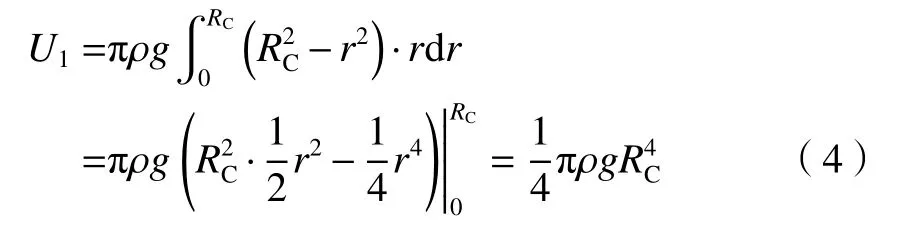
由于冠部体积和液坑体积相等，可得：

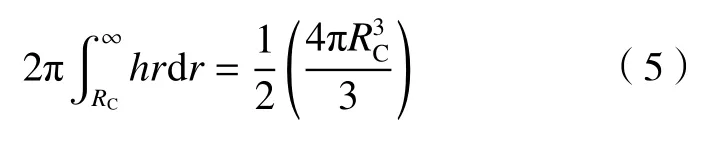
其中，h为冠部顶点与液面的距离。冠部表面轴对称剖面的曲线方程为[20]：

积分可得冠部的重力势能U2：

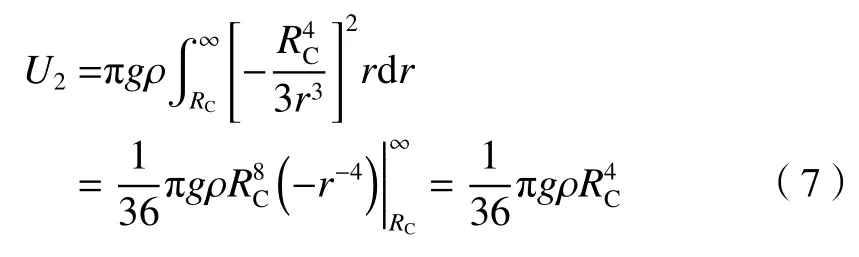
因此，当液坑体积达到最大时系统的重力势能U为：

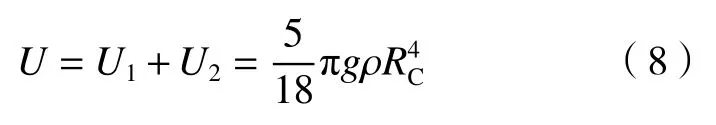
其中，RC=H。

对于完整液坑，图9给出了由式（3）和（8）计算的系统总能量E与液坑最大时的系统重力势能U的关系。U随E增大而增大，近似线性变化，即U占E的比例相对固定。可以看出：E较小时，d对这一比例影响较小；E增大时，影响变大。从图9（a）～（d）可以看出，d对U占E的比例有所影响，d越大，U占E的比例越高。从图9（e）～（g）可以看出，U占E的比例与h0和d有关。h0从40 mm 到15 mm，U占E的比例增大，但h0降至10 mm 时，比例明显减小。

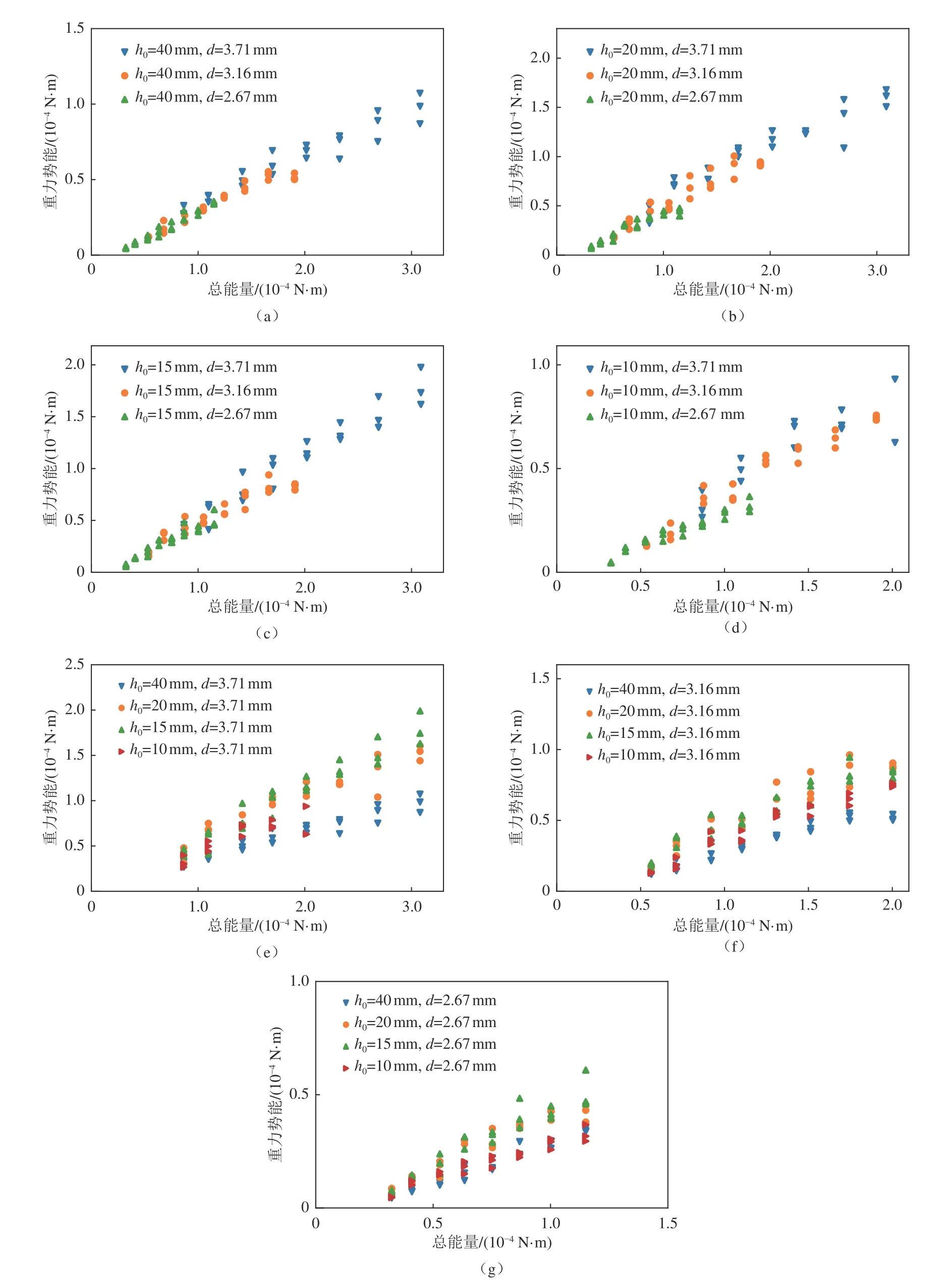
图9 完整液坑系统重力势能与总能量的关系（a～d：不同液滴直径；e～g：不同液池深度）Fig.9 Relationship between gravitational potential energy and total energy of complete crater (a-d:different droplet diameters; e-g:different liquid pool depths)

3.3.2 非完整液坑（液坑触底）

对于非完整液坑的重力势能，尚未见文献分析。根据本文实验观察到的现象，可将非完整液坑简化为一个底部被切掉一部分的半球，如图4（b）所示。与完整液坑相同，系统的总能量E仍等于液滴的初始动能。液坑的重力势能U1为：

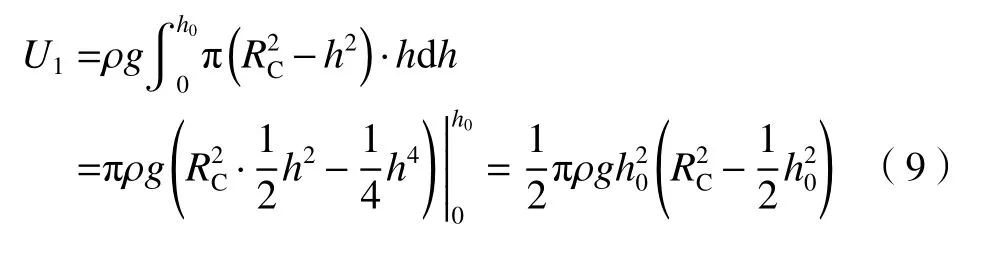
由于冠部体积和液坑体积相等，可得：

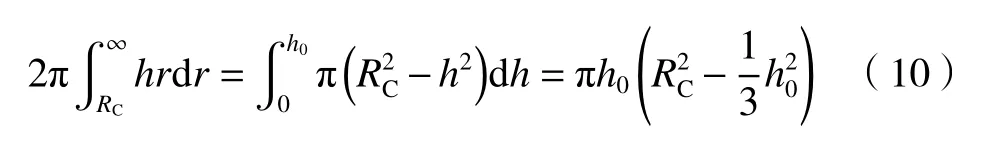
式（10）和（5）的左端积分项相同，借鉴求解式（5）的方法[20]，可设满足式（10）的解为：

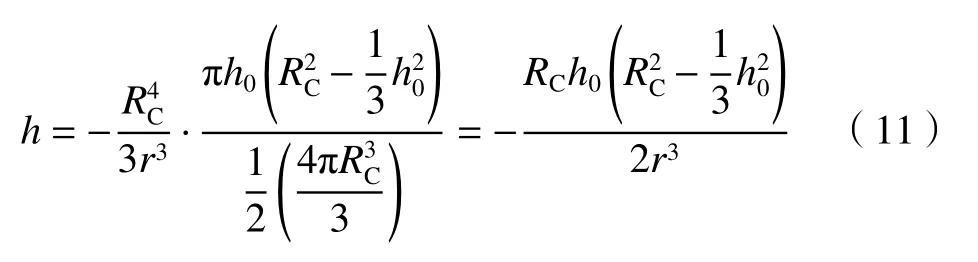
积分可得冠部的重力势能U2：

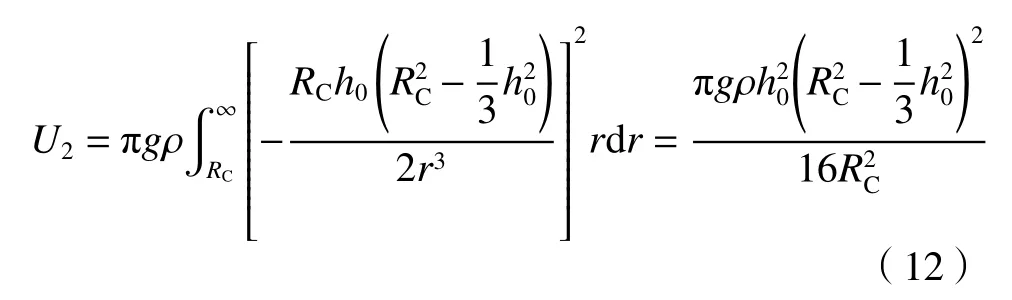
非完整液坑体积达到最大时系统的重力势能U为：

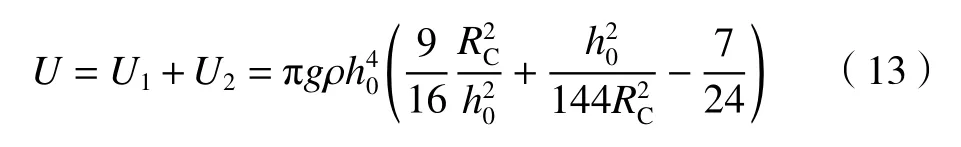
对于非完整液坑，图10给出了由式（3）和（13）计算的重力势能U与总能量E的关系。h0=5 mm 时，U随E增大而增大，d对其稍有影响，d越大，U越大。h0=10 mm 时，U比h0=5 mm 时明显更高。

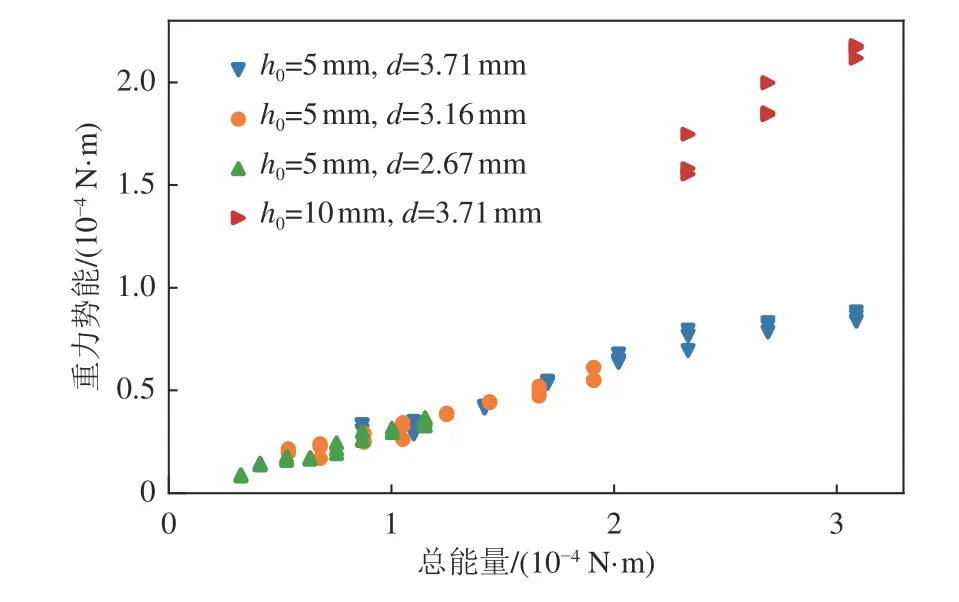
图10 非完整液坑系统重力势能与总能量的关系Fig.10 Relationship between gravitational potential energy and total energy of incomplete crater

4 结 论

本文对液滴撞击液面的运动过程进行了实验研究，重点探讨了液滴直径d和液池深度h0对液坑最大水平长度L和最大深度H的影响，对已有的液坑重力势能模型进行了扩展。主要结论如下：

1）液滴撞击液池会产生液坑和液柱。液池较深时，液坑近似半球形；液池较浅时，液坑不能充分发展，形状近似横切掉底部的半球。液池较深时，液柱较粗且低，分离出的次生液滴较少（1～2 个），向上运动速度较小；液池较浅时，液柱较高且细，分离出的次生液滴更多（可多至9 个），向上运动速度较大。

2）液坑无量纲最大水平长度L/d和无量纲最大深度H/d均随We增大而增大，d越大，L/d和H/d越小；液池较深时（40、20 和15 mm），L/d和H/d随h0减小而增大，h0达到10 mm 时，L/d和H/d明显减小。

3）液坑的重力势能U随总能量E增大而增大，液滴直径d越大，U占E的比例越高。液池较深时（40、20 和15 mm），液坑重力势能随h0减小而增大；液池较浅时（10 和5 mm），液坑重力势能与液滴的初始动能比值更低。