数字空间联结的灵活性及其内在机制*

颜丽珠 陈妍秀 刘 勋 傅世敏 南威治

·研究前沿(Regular Articles)·

数字空间联结的灵活性及其内在机制*

颜丽珠1陈妍秀1刘 勋2傅世敏1南威治1

(1广州大学教育学院心理系/脑与认知科学中心, 广州 510006) (2中国科学院行为科学重点实验室, 北京 100101)

数字空间联结一直是认知心理学领域研究的热点之一。探索数字空间联结的一个重要指标为空间−数字反应联合编码(spatial-numerical association of response codes, SNARC)效应(左/右手对小/大数反应更快更准确)。以往研究已验证SNARC效应的普遍性及其在方向上的灵活性, 并提出多种理论解释。此外, SNARC效应在加工阶段上也具有灵活性, 其原因可能有：(1)加因素法则的理解偏差; (2)观察的角度单一; (3)观察效标的差异; (4)使用任务的差异。结合以上因素, 提出双阶段(数量信息的空间表征、空间表征到反应选择)加工模型, 不同的操控因素分别作用于两个阶段可能是引起SNARC效应灵活变化的核心原因。未来研究可从对比任务差异、引入不同干扰因素等方面进一步验证双阶段加工模型, 并结合认知神经科学技术揭示数字空间联结灵活性的内在神经机制。

SNARC效应, 灵活性, 数字空间联结, 双阶段加工模型

1 引言

数字与人类社会同在, 是正常生活的必要工具。早在原始社会, 人类就用石子或绳结来计数。到现代社会, 数字被用来表示身高、体重等, 甚至组成证件号来表示人们独一无二的身份。人们使用数字去描述、认识和理解世界。心理学家也试图解答大脑如何表征和加工数字的问题, 探究人类理解、产生和计算数字时的心理过程(Dehaene, 1989, 1992; Moyer & Landauer, 1967)。

数字与空间的联结是数字加工的一个重要方面, 对其进行研究有助于了解数字的加工过程(徐晓东, 刘昌, 2006)。Galton (1880)分析了一些内省报告, 首次指出数字具有空间特性。Seron等人(1992)也发现大多数被试对从小到大的数字具有从左到右的心理表征。除了这些内省证据, 也有行为证据表明数字具有空间表征(Brysbaert, 1995; Fias et al., 1996; Ratinckx & Brysbaert, 2002)。数字空间联结研究领域内一个里程碑式的进展是空间−数字反应编码联合(spatial-numerical association of response codes, SNARC)效应的发现, 即左手相比于右手对小数反应更快更准确, 右手相比于左手对大数反应更快更准确(Dehaene et al., 1993)。SNARC效应作为实验指标, 清晰地表明数字空间联结的存在, 反映出小数与左侧空间、大数与右侧空间有更强联结。

2 SNARC效应的普遍性和灵活性

2.1 SNARC效应存在普遍性

Dehaene等人(1993)最早在判断数字0～9奇偶性质的实验中发现SNARC效应。此后SNARC效应得到了广泛研究, 包括数字范围、实验材料、感觉通道、反应方式和反应指标等方面(康武等, 2013)。在数字范围方面, SNARC效应不仅发生在个位数(Dehaene et al., 1993; Moro et al., 2018; Zhao et al., 2018), 也扩展到了双位数(Brysbaert, 1995; Fitousi & Algom, 2020)、负数(韩萌等, 2017; Kong et al., 2012)、数词(Nuerk et al., 2005; 乔福强等, 2016)和分数(孙玉等, 2016)等。在实验材料方面, SNARC效应不仅发生在数字上, 也发生在字母(Gevers et al., 2003; Lonnemann et al., 2013)、音符(Prpic et al., 2016)、音高(Weis et al., 2016)、时间(He et al., 2020; Zhao et al., 2018)、逻辑推理(Prado et al., 2008)、面积和亮度(Fumarola et al., 2014; 胡林成, 熊哲宏, 2011)等具有顺序信息的材料上。在感觉通道方面, Nuerk等人(2005)要求被试判断四种不同形式数字的奇偶性质, 包括点阵、阿拉伯数字、视觉呈现的德语数字、听觉呈现的德语数字, 结果均发现SNARC效应, 第一次证明该效应存在于除视觉之外的其他感觉通道中; 除此之外, Krause等人在触觉通道中也发现了SNARC效应(Krause et al., 2014)。在反应方式方面, 在双手反应(Rusconi et al., 2011; Shaki & Gevers, 2011)、双手交叉反应(Dehaene et al., 1993; Viarouge et al., 2014)、单手反应(Riello & Rusconi, 2011)和双脚踏板(Hartmann et al., 2014)等反应方式上都能观察到SNARC 效应。在反应指标方面, SNARC效应不仅出现在反应时上, 也在眼动轨迹(Myachykov et al., 2015; Pressigout et al., 2019; 司继伟等, 2013)、脑电(Keus et al., 2005)、磁共振成像(Tschentscher et al., 2012; Weis et al., 2015)、近红外成像(Cutini et al., 2014)等指标上出现。Keus等人(2005)通过数字奇偶判断任务观测脑电指标, 发现SNARC效应不一致条件相比于一致条件, 在Cz和Pz电极上的反应锁定的单侧化准备电位(lateralized readiness potential, LRPs)出现更负的波幅。韩萌等人(2017)在负数材料上发现SNARC效应不一致条件比一致条件诱发了更负的P3。溯源分析进一步将SNARC效应定位于额叶与顶叶。数字加工的磁共振成像研究表明, 无论在视觉刺激或非视觉刺激, 无论在符号数字或非符号数字, 顶内沟都会被激活(Cohen Kadosh & Walsh, 2009; Dehaene et al., 2004)。这些研究说明SNARC效应, 即数字与空间联结这一现象, 具有普遍性。

2.2 SNARC效应存在灵活性

此外, SNARC效应还在方向和发生阶段方面具有一定的灵活性。不同的操控因素从不同角度影响SNARC效应的发生过程, 使其在方向和发生阶段上发生变化, 表现出SNARC效应具有一定的灵活性。(1)方向的灵活性。研究者们发现不同被试的阅读习惯(从左向右阅读或从右向左阅读等) (Dehaene et al., 1993)、变化的数字范围(1～9、0～4、4～9等) (Dehaene et al., 1993; Fias et al., 1996)、不同的表征方式(直尺或闹钟等) (Bächtold et al., 1998)、工作记忆序列位置(Fias & van Dijck, 2016)和比较大小的参照标准(Zhang et al., 2020)等因素都会影响SNARC效应的方向。如Dehaene等人(1993)在从左到右阅读习惯的被试上观察到小数左手按键更快和大数右手按键更快的经典SNARC效应, 而在从右到左阅读习惯的被试上观察到大数左手按键更快和小数右手按键更快的反向SNARC效应。(2)发生阶段的灵活性。研究者们从SNARC效应与发生在不同阶段的效标(如Simon效应、Stroop效应、数字距离效应、转换成本效应等)的关系、SNARC效应在不同反应方式上的变化(双手反应或眼动等)、以及SNARC效应诱发的脑电成分等三个角度试图确定SNARC效应的发生阶段(早期刺激表征阶段或晚期的反应选择阶段), 但研究结果仍存在争议(Nan et al., 2021)。一些研究结果表明SNARC效应发生在早期刺激表征阶段(Fischer et al., 2004; Mapelli et al., 2003; Tlauka, 2002), 另一些研究结果则支持其发生在晚期反应选择阶段(Daar & Pratt, 2008; Gevers et al., 2005; Gevers, Ratinckx et al., 2006; Keus et al., 2005; Keus & Schwarz, 2005; Yan et al., 2021), 最新的一些研究则认为其灵活地发生在这两个阶段(Moro et al., 2018; Nan, et al., 2021; Zhang et al., 2020)。下文将从这两点灵活性展开具体论述并总结其原因。

3 SNARC效应方向的灵活性及理论解释

Dehaene等(1993)提出了心理数字线(Mental Number Line)来解释SNARC效应及其方向的灵活性, 但该假设并不能完全解释SNARC效应的所有研究结果(Bächtold et al., 1998; van Dijck et al., 2009), 对此一些研究者也提出如极性编码理论(Proctor & Cho, 2006)、双路径模型(Gevers, Verguts, et al., 2006)、工作记忆序列位置(Fias & van Dijck, 2016)、神经网络模型(Chen & Verguts, 2010)和大脑半球偏侧化(Vallortigara, 2017)等假设做进一步解释。

3.1 早期理论解释

3.1.1 心理数字线解释

心理数字线假设认为数字在大脑中被表征成一条从左到右的向量, 小数在左, 大数在右, 因此数字与空间联结, 产生内在空间属性。SNARC效应反映了数字和反应二者空间属性的兼容性(Brysbaert, 1995; Dehaene et al., 1990; Vu & Proctor, 2001), 当数字的左/右空间属性与参与者的左/右反应一致时, 反应较快, 反之, 反应变慢(Cutini et al., 2014; Dehaene et al., 1993; Fischer & Shaki, 2014; 康武等, 2013; Moro et al., 2018)。

研究者们认为阅读和书写习惯是心理数字线在长时记忆中形成的原因之一, 因此不同方向的阅读和书写习惯会引起不同的数字空间联结模式(Dehaene et al., 1993; Fischer et al., 2010; 李雅君等, 2018; 刘雍江等, 2018)。Dehaene等人(1993)在法国被试(从左到右的阅读习惯)上观察到经典的SNARC效应, 而在伊朗被试(从右到左的阅读习惯)上出现了反向的SNARC效应。在垂直方向上, 也有研究发现与阅读和书写习惯相同方向的数字空间联结模式(Gevers,Lammertyn, et al., 2006; Hung et al., 2008; Schwarz & Keus, 2004; Seron et al., 1992)。

但也有与阅读和书写习惯的解释相悖的证据, Ito和Hatta (2004)在日本被试(自上而下的阅读习惯)观察到与阅读习惯反向的数字空间联结模式。Dehaene等人(1993)和Fias等人(1996)发现数字范围改变SNARC效应的方向, 即在0～5范围内, 数字4为相对大数, 右手对数字4反应更快, 而在4～9范围内, 数字4为相对小数, 左手对数字4反应更快。Bächtold等人(1998)发现数字的表征方式也会改变SNARC效应的方向, 即要求被试(从左到右的阅读习惯)分别想象数字以直尺(小数在左侧)或钟表(小数在右侧)的形式排列时, 分别观察到了经典SNARC效应和反向的SNARC效应。van Dijck等人(2009)发现数字在工作记忆中的序列位置也会改变SNARC效应的方向, 即在任务前要求被试记忆一串数字, 结果发现记忆中数字的前/后位置与左/右空间形成联结, 左手对前位置的数字反应更快, 右手对后位置的数字反应更快, 与数字的大小信息无关。Zhang等人(2020)发现参照标准也会改变SNARC效应的方向, 即以3和7作为参照线索, 要求被试比较随后出现的目标数字与线索的大小发现, 与3比较时, 4、5和6为相对大数, 出现右手相比于左手反应更快的SNARC效应; 与7比较时, 4、5和6为相对小数, 出现左手相比于右手反应更快的反向的SNARC效应。因此, 长时记忆中的心理数字线假设并不能解释全部的数字空间联结现象(Abrahamse et al., 2016)。

3.1.2 极性编码理论

Proctor和Cho (2006)首次提出极性编码理论, 认为语义概念之间的联结决定了SNARC效应。在二元分类任务中, 刺激和反应通常被编码为正极和负极。因此, 在SNARC效应中, 在概念上, “右”、“上”与“大”同属于正极, “左”、“下”与“小”同属于负极。当刺激分类(如“大”)和反应位置(“右”)极性一致时, 反应选择更快, 反之变慢。虽然在二分类任务中, 极性编码理论比心理数字线解释了更多研究结果, 相对大小的分类解释了不同数字范围的影响(Dehaene et al., 1993; Zhang et al., 2020), 但仍不能解释表征方式、工作记忆序列位置的相关研究。

3.1.3 双路径模型解释

Verguts等人(2005)为了解释和整合数字认知中的一些发现, 提出了数字认知的联结模型, 其中位置编码、线性缩放和心理数字线的固定变化是关键特征。Gevers等人(2006)整合并扩展了极性编码理论和联结模型, 提出了双路径的计算模型。该模型认为数字加工包含两条并行的信息加工路径：无条件路径和条件路径。(1)在无条件路径中, 存在于长时记忆中的数字大小信息和空间方位信息的联结被自动激活; (2)在条件路径中, 根据当前任务要求, 数字被编码为任务相关的二进制类别(如奇偶判断), 数字类别与当前任务要求的映射关系在短时记忆中被激活。SNARC效应产生于两条路径激活的反应之间的协同性。如果任务相关的映射规则与长时记忆的数字空间联结一致, 两条路径就会合作, 反应更快; 否则就会竞争, 反应更慢。因此, 当任务要求的数字表征方式发生变化(直尺或钟表)时, 会观察到不同方向的SNARC效应(Bächtold et al., 1998)。

3.2 近期理论解释

3.2.1 工作记忆解释

除以上早期理论, 一些研究者进一步引入工作记忆中的序列位置来解释数字空间联结现象(Abrahamse et al., 2016; Fias & van Dijck, 2016; van Dijck & Fias, 2011; van Dijck et al., 2009)。该假设认为：工作记忆中的数字序列位置的空间编码诱发了SNARC效应, 即工作记忆中的数字序列的前/后位置与左/右空间形成联结, 产生一条短时的新的心理数字线, 该数字线相比于长时记忆中的心理数字线表征更强, 因此实验者只能外显地观察到与短时的心理数字线对应的SNARC效应, 其方向可能与长时记忆中的心理数字线相同, 也可能与之相反。Lindemann等人(2008)、Herrera等人(2008)和van Dijck等人(2009)最早证实了工作记忆中的心理数字线在SNARC效应的发生上起着重要作用。工作记忆序列位置假设在早期理论的基础上, 进一步阐释了SNARC效应方向变化的原因(邓之君等, 2017)。

3.2.2 神经网络模型解释

Chen和Verguts (2010)在双路径模型的基础上引入了文化因素和生理因素(即侧顶叶, lateral intraparietal area, LIP)进一步扩展补充双路径模型, 提出了数字空间联结的神经网络模型。该模型提出促使SNARC效应产生的两个原因：一是由于自动触发的大小反应, 小/大分别与左/右联结; 二是由于数字与空间的相互作用, 在LIP中, 小数字优先激活左空间编码单元, 促进了“左”反应, 大数字与之对应。这种双源假设得到了Gevers等人(2010)与van Dijck等人(2009)的研究证实, 即语言——空间反应编码与视觉——空间反应编码对SNARC效应都有贡献。

3.2.3 大脑半球偏侧化的生物学解释

另外, 在单侧忽视症病人(Zorzi et al., 2002)、学龄前儿童(van Galen & Reitsma, 2008)、婴儿(Bulf et al., 2016)、甚至新生儿(Giorgio et al., 2019)和动物(Drucker & Brannon, 2014)等无语言能力群体中也能观察到数字空间联结现象。这些研究进一步质疑了早期理论的解释。Vallortigara (2017)提出了一个依靠大脑半球特殊化的情绪效价的理论：少/大量的物品分别会引发消极/积极的情绪, 优先调动右/左半球, 从而分别导致左/右侧的行为偏差。Felisatti等人(2020)基于动物大脑对不同空间频率的非对称调节, 提出数字空间联结的生物学机制, 即视觉模式中包含较少/多元素的空间频率会优先占用右/左大脑半球, 引起左/右行为偏差, 并在新生儿中得到验证。Zhou等人(2020)在语义任务(奇偶判断和水果−蔬菜分类)中发现左手偏侧化效应, 而在大小比较任务中没有观察到左手偏侧化, 也进一步推断这种差异可能与大脑半球的偏侧化以及空间编码的任务相关性的综合作用有关。

4 SNARC效应发生阶段的灵活性及可能原因

SNARC效应除了方向存在灵活性以外, 其发生阶段的定位也一直存在争议。信息加工理论表明, 感官从刺激呈现到反应可以分为一系列阶段：刺激表征、反应选择和反应执行等(Duncan, 1980; Marois et al., 2006; Tombu et al., 2011)。对于SNARC效应发生阶段的定位, 研究者们主要提出了三种观点, (1)发生在刺激表征阶段(Tlauka, 2002), (2)发生在反应阶段(Daar & Pratt, 2008; Yan et al., 2021), (3)既发生在刺激表征阶段, 又发生在反应选择阶段(Moro et al., 2018; Zhang et al., 2020; Nan et al., 2021)。

4.1 刺激表征阶段的证据

第一种观点认为SNARC效应发生在刺激表征阶段(Fischer et al., 2004; Mapelli et al., 2003; Tlauka, 2002)。主要有以下三个方面的证据：首先, SNARC效应与发生在反应选择阶段的Simon效应在反应时上没有交互作用(Mapelli et al., 2003; Tlauka, 2002)。以往研究表明, 经典的Simon效应(左/右手对左/右侧空间刺激反应更快)被验证发生在反应选择阶段(De Jong et al., 1994; 金桂春等, 2017; Leuthold, 2011)。根据加因素法则(若两个过程发生在同一阶段, 两者会表现出交互; 反之两者独立) (Liu et al., 2010; Sternberg, 1969), Tlauka (2002)和Mapelli等人(2003)分别通过对呈现在屏幕左/右侧的目标数字进行左/右按键反应来诱发SNARC和Simon效应, 两个研究都发现两种效应在反应时上没有交互作用。因此推断SNARC效应可能发生在与Simon效应不同的早期刺激表征阶段。其次, 在与左右空间无关的中央反应方式上观察到SNARC效应(Fischer et al., 2004)。Fischer等人(2004)在没有左右区分的中央反应(眼动)上也观察到了SNARC效应, 说明SNARC效应可能发生在与刺激表征加工相关的早期阶段, 而非与反应相关的晚期阶段。此外, Pinto等人(2019)使用go/no-go任务发现, 只有发生在刺激表征阶段的空间编码和数字大小编码被同时使用时, 才能观察到SNARC效应, 说明SNARC效应可能发生在早期刺激表征阶段。第三, 脑电研究发现SNARC效应可诱发N1、P1等早期成分的变化(Gut et al., 2012; Schuller et al., 2014)。Gut等人(2012)通过数字Flanker任务同时诱发SNARC和Flanker效应, 观察到SNARC效应的不一致条件产生的早期N1成分的波幅显著大于一致条件, 认为SNARC效应最早产生于顶枕部的N1成分。Schuller等人(2014)也发现, 当用数字作为提示时, 发现数字可以引导注意偏向(小数向左、大数向右), 并且在早期P1成分上也发现注意偏向效应。

4.2 反应选择阶段的证据

第二种观点认为SNARC效应发生在反应选择阶段(Daar & Pratt, 2008; Gevers et al., 2005; Gevers et al., 2006; Keus et al., 2005; Keus & Schwarz, 2005; Yan et al., 2021)。

与第一种观点三个方面的证据对应, 首先, SNARC效应与发生在反应选择阶段的Simon效应在反应时上有交互作用(Gevers et al., 2005)。Gevers等人(2005) 同样采用加因素法则, 重复了Mapelli等人(2003)的实验, 观察到SNARC、Simon与反应时分布的三重交互, 说明随着反应时的增加, SNARC与Simon效应发生交互作用, 由此推断两者可能发生在相同加工阶段, 即晚期反应选择阶段。Yan等人(2021)也在奇偶判断任务中观察到SNARC和Simon效应的交互作用, 支持SNARC效应发生在晚期反应选择阶段的推论。其次, SNARC效应只出现在左右手反应上, 而不出现在中央反应方式上(Keus & Schwarz, 2005)。Keus等人(2005)操控刺激的呈现位置(两侧/中心)和反应方式(中央反应的口头/左右手按键), 发现SNARC效应与呈现位置无关, 只发生在左右手按键反应方式中, 而没有发生在中央的口头报告反应上, 说明SNARC效应与左右空间的反应存在联结, 更可能发生在反应选择阶段。第三, 脑电研究发现SNARC效应可诱发P300、LRP等晚期成分的变化(Keus et al., 2005; Gevers et al., 2006)。Keus等人(2005)通过脑电实验发现SNARC效应对反应选择相关的单侧化准备电位(LRP)成分存在影响。Gevers等人(2006)重复了Keus等人(2005)的实验进一步发现LRP成分在刺激锁时(s-LRP), SNARC效应的一致条件比不一致条件的起始潜伏期显著更早, 而在反应锁时(r-LRP)两种条件没有显著差异, 进一步为SNARC效应发生在反应选择阶段提供证据。

除此之外, 徐晓东和刘昌(2006)从行为、电生理两方面详细论述了前人的研究, 总结多数证据是支持SNARC效应发生于反应选择阶段。Müller和Schwarz (2007)通过心理不应期范式要求被试完成奇偶判断任务和音调辨别任务, 发现SNARC效应不随SOA (stimulus onset asynchrony, 指从启动刺激呈现起到目标刺激呈现之间的时间)的变化而变化。Daar和Pratt (2008)使用自由选择范式, 让被试对屏幕中央的数字自由按左/右键, 发现被试倾向于对小数按左键, 对大数按右键, 体现了数量信息和反应选择的直接关系。Didino等人(2019)要求被试完成语义加工任务和非语义加工任务来验证语义加工是否会影响SNARC效应, 结果发现SNARC效应并不受到语义加工影响, 而受到反应延迟的影响, 反应越慢, 效应越强。以上研究都支持SNARC效应发生在反应选择阶段的推断。

4.3 同时发生于两个阶段的证据

除了以上两种认为SNARC效应发生在某一固定加工阶段的观点以外, 近几年的研究结果趋向形成一个新观点, 即SNARC效应可能不是单一出现在某一阶段,而是既发生在刺激表征阶段, 又发生在反应选择阶段(Moro et al., 2018; Nan, et al., 2021; Zhang et al., 2020)。Moro等人在SNARC效应中引入发生在刺激表征阶段的数字距离效应(van Opstal & Verguts, 2011)和发生在反应选择阶段的转换成本效应(Hirsch et al., 2017), 考察三者之间的交互作用来验证SNARC效应的发生阶段。结果观察到SNARC效应与转换成本效应(反应选择相关)存在交互作用, 以及SNARC、距离效应(刺激表征相关)和反应时分布也存在三重交互。Zhang等人(2020)同样也观察到了SNARC效应与反应规则(反应选择相关)和距离效应(刺激表征相关)的三重交互。Nan等人(2021)通过改进的数字大小比较任务, 引入发生在刺激表征阶段的手动Stroop效应(Li et al., 2014)和发生在反应选择阶段的Simon效应, 结果观察到SNARC效应既与Stroop效应发生交互, 又与Simon效应发生交互。以上结果都支持SNARC效应既发生在刺激表征阶段又发生在反应选择阶段的推论。在脑电指标上, 韩萌等人(2017)在同一实验的不同条件下观察到SNARC效应灵活地出现在两个阶段。他们在大小比较任务中考察目标数字与基线数字(±5)的符号异同对SNARC效应的影响, 观察到当目标数字与基线数字正负号相同时, 不一致比一致条件诱发了更负的 P300, 即SNARC效应发生于反应选择阶段; 当目标数字与基线数字正负号相异且基线数字为+5时, 不一致比一致条件诱发了更负的 N300, 说明SNARC效应发生在刺激表征阶段; 而基线数字为–5时, 一致比不一致条件诱发了更正的晚期正电位(late positive potential, LPP), 说明SNARC效应发生在反应执行阶段。

4.4 发生阶段存在灵活性的可能原因

以往研究关于SNARC效应的发生阶段一直存在争议, 可能是由以下四个原因造成。

第一, 对加因素法则的理解偏差导致间接推论。前人大多通过SNARC效应与Simon效应的关系来确定其加工阶段(Gevers et al., 2005; Mapelli et al., 2003; Scerrati et al., 2017; Stroop, 1935)。根据加因素法则, SNARC与Simon效应没有交互作用, 只能说明两者没有发生在同一加工阶段, 而SNARC效应发生在早期刺激表征阶段的结论属于间接推论。若要直接推论, 必须全面观察其加工阶段, 可以同时引入发生在刺激表征阶段和发生在反应选择阶段的两种效应(Moro et al., 2018; Nan et al., 2021; Yan et al., 2021), 全面考察SNARC效应与两种效应之间的关系, 从而直接确定其发生阶段。近几年支持SNARC效应发生在两个阶段的研究均是采用同时引入两种效应的逻辑(Moro et al., 2018; Nan et al., 2021; Yan et al., 2021)。

第二, 观察的角度单一导致间接推论。除了以上结合SNARC效应和Simon效应的研究外, 其他探究SNARC发生阶段的研究大多只从一个角度来观察其发生阶段。例如, Fischer等人(2004) 在没有左右区分的中央反应(眼动)观察到SNARC效应, 推测其可能发生在与刺激表征加工相关的早期阶段; Schuller等人(2014) 用数字作为线索提示, 发现数字可以引导注意偏向(小数向左、大数向右), 并且在早期P1成分上也发现注意偏向效应, 推断数字空间联结发生在信息加工的早期阶段; Daar和Pratt (2008)让被试对屏幕中央的数字自由按左/右键, 发现被试倾向于对小数按左键,对大数按右键, 体现了数量信息和反应选择的直接关系。Keus等人(2005)和Gevers等人(2006)发现SNARC效应可诱发P300、LRP等晚期成分的变化。这些研究支持SNARC效应发生在刺激表征阶段或反应选择阶段, 但它们存在与第一点相似的问题, 其只能说明SNARC效应发生在某一阶段, 但并不能说明不发生在其他阶段。

第三, 研究采用了不同类型的Simon效应作为效标, 二者发生机制有所不同, 导致观察结果的差异。Simon效应根据刺激空间属性的感知方式分为两种类型：视觉运动Simon效应和认知Simon效应(王力等, 2012; Wang et al., 2014; Wiegand & Wascher, 2005)。二者在反应时分布分析(Response Time Distribution Analysis)、与手近效应的关系和脑电成分LRP成分上均有较大区别。视觉运动Simon效应由刺激的空间位置信息诱发, 但由于视觉刺激的作用消逝较快, 其诱发的效应会随着反应时的延长而减小、消失甚至反转, 且受到手近效应调节(当反应手距离刺激近时效应变大, 距离远时效应变小), 在脑电上也观察到在不一致条件下LRP成分的早期偏移。认知Simon效应由认知编码的空间位置信息诱发, 认知编码的作用时间较长, 其诱发的效应会随着反应时的延长而保持稳定甚至增大, 且不受到手近效应的调节, 在不一致条件下也不会出现LRP的早期偏移(Wiegand & Wascher, 2005, 2007)。以往研究SNARC与Simon效应的关系时, 多采用随着反应时增大而变小的视觉运动Simon效应, 因此观察到SNARC与Simon效应时而无交互、时而在时间进程上有交互等不同现象(Gevers et al., 2005; Keus & Schwarz, 2005; Mapelli et al., 2003; Treccani et al., 2010), 而采用认知Simon效应的研究则均稳定地观察到SNARC与Simon效应的交互(Nan et al., 2021; Yan et al., 2021)。未来研究应考虑结合认知Simon效应来考察SNARC效应与之的关系, 以确定其发生阶段。

第四, 研究使用的任务不同, SNARC效应发生的通路有所不同, 导致观察结果的差异。观察SNARC效应的常用范式有数字奇偶判断任务和数字大小比较任务, 二者对于数量信息的加工不同, SNARC效应的内在产生过程在两种任务中有所区别(见图1) (Dehaene et al., 1993; Deng et al., 2018; Deng et al., 2017; Gevers, Lammertyn, et al., 2006)。在数字奇偶判断任务中, 被试只需判断奇偶性质, 无需加工数量信息, 因此对数量信息的加工是内隐的(任务无关)。在该任务中, 数量信息自下而上地被自动化加工并产生心理数字线表征, 数字在心理数字线上的位置和当前反应构成冲突产生SNARC效应。而在数字大小判断任务中, 被试只需判断数量大小才能做出正确反应, 因此对数量信息的加工是外显的(任务相关)。在该任务中, 数量信息自上而下地被有意加工并产生心理数字线表征, 诱发SNARC效应。Deng等人(2018)年还在反应时间进程上观察到, 随着反应时间的变大, 奇偶判断任务中效应量表现出上下波动的模式, 而大小比较任务中SNARC效应出现更早, 且保持稳定甚至效应量变大的模式。Nan等人通过结合SNARC、Simon (反应选择相关)和Stroop (刺激表征相关)三种效应, 发现在奇偶判断任务中, SNARC和Simon效应发生交互, 支持SNARC发生在反应选择阶段的推论(Yan et al., 2021); 而在大小比较任务中, SNARC既与Simon效应交互, 又与Stroop效应交互, 支持SNARC同时发生在这两个阶段的推论(Nan et al., 2021)。

4.5 双阶段加工模型

对于SNARC效应发生阶段灵活变化的现象, 以往的理论并没有着重解释。因此, 本综述在SNARC效应前期模型的基础上, 提出一个双阶段加工的概念模型(图1), 尝试进一步解释SNARC效应发生阶段的灵活性问题。

模型具体包含三层结构, 底层是输入层, 包括数字的数量信息和奇偶信息的输入; 中间层是表征层, 输入层的信息在该层进行数量表征和奇偶表征, 并且数量表征会进一步产生空间表征; 上层是反应输出层, 接收表征层的输入, 根据任务要求对出现的数字进行反应。双阶段加工模型认为SNARC效应既发生在刺激表征阶段又发生反应选择阶段, 这两个阶段可进一步具体表现为数量信息的空间表征阶段和数量的空间表征到反应选择阶段。任何因素若干扰这两个阶段, 都会影响SNARC效应的产生及其效应量大小, 从而表现出以往研究中观察到的不同形式的SNARC效应及它与其他效应之间的不同关系。

我们将以往观察到的不同实验结果归因到不同因素对SNARC效应两个阶段的影响, 从而造成SNARC效应灵活变化的现象：

(1)长时记忆、工作记忆负载、任务类型、Stroop任务等与表征相关的因素影响了数量信息的空间表征阶段。长时记忆的阅读习惯影响数字信息的空间表征阶段, 因此从左到右阅读的个体出现从左到右的SNARC效应, 而从右到左阅读的个体反之(Dehaene et al., 1993)。由于认知资源有限, 高工作记忆负载影响数字的数量表征到空间表征的过程, 引起SNARC效应消失甚至反转(van Dijck & Fias, 2011)。任务类型也会影响这个阶段, 如在颜色判断任务中, 被试判断数字的颜色时没有对数字进行深入表征和加工, 数量信息与空间信息没有得到足够表征, 因此没有观察到SNARC效应(Didino et al., 2019)。以背景汉字“大小”与数字的大小信息诱导产生大小Stroop效应, 此时背景汉字也输入了“大小”信息, 影响了该阶段, 因此观察到SNARC与Stroop发生交互作用(Nan et al., 2021)。

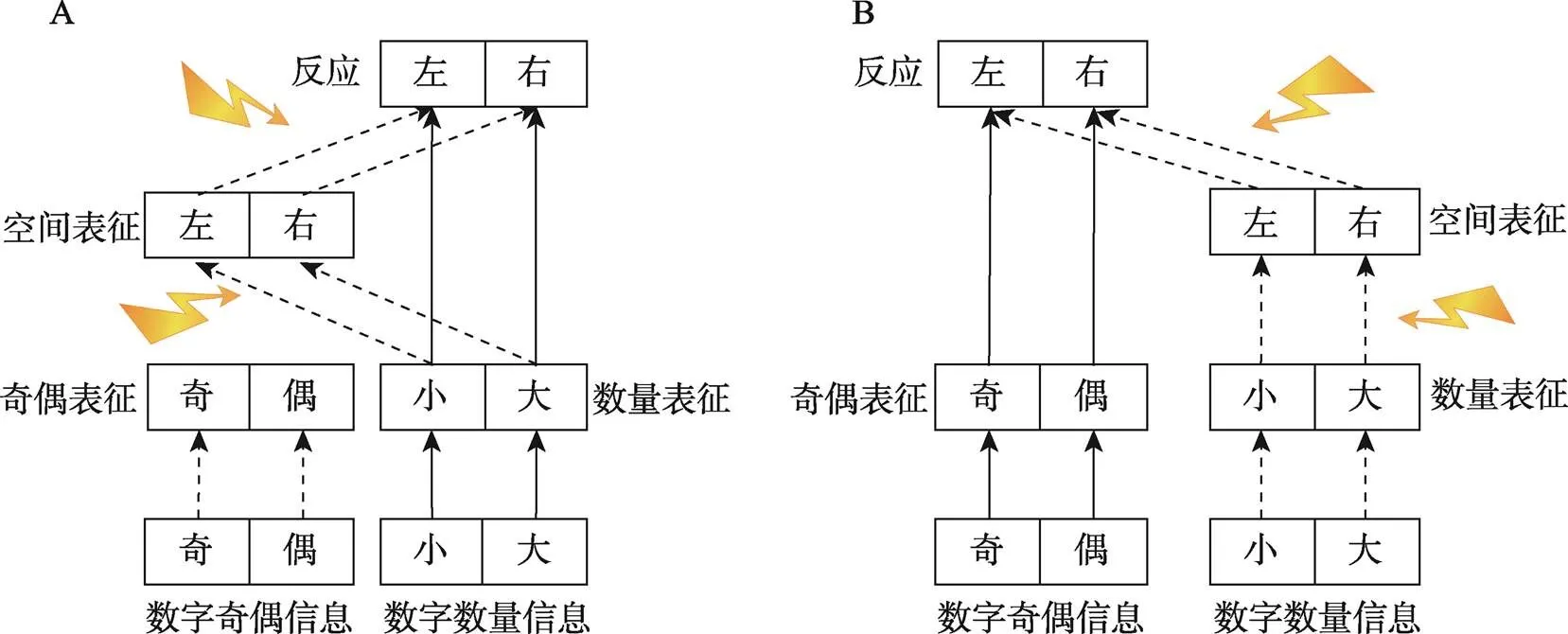
图1 大小比较任务和奇偶判断任务中SNARC效应的双阶段加工模型。实线表示任务相关信息的加工通路, 虚线表示任务无关信息的加工通路, 闪电箭头表示SNARC效应产生链路的任一环节施加不同形式的干扰因素都会影响效应的产生。图A表示大小比较任务, 数量信息为任务相关信息输入, 奇偶信息为任务无关信息输入; 图B表示奇偶判断任务, 奇偶信息为任务相关信息输入, 大小信息为任务无关信息输入。

(2) Simon任务和反应规则切换等与反应相关的因素影响了数量的空间表征到反应选择阶段。在SNARC和Simon效应结合的任务中, 当数字呈现在屏幕左右两侧时, 数字的空间位置影响数字的空间表征, 进一步干扰了空间表征到反应选择阶段, 进而使得SNARC效应可能消失(金桂春等, 2017)。反应规则的切换影响了反应选择, 干扰了空间表征到反应选择阶段, 表现出SNARC效应与转换成本交互的模式(Moro et al., 2018; Zhang et al., 2020)。

双阶段加工模型区别了大小比较和奇偶判断不同任务下, 大小信息作为任务相关与任务无关信息的加工路径差异, 提出多种不同的操控因素从不同角度影响了SNARC效应发生的两个阶段而使其发生变化, 较为完整地涵盖并解释了以往研究观察到的SNARC效应灵活变化的现象。

5 总结与展望

5.1 研究总结

SNARC效应作为一个实证指标, 被广泛运用于实验研究中来验证数字不仅包含了数量信息, 还传递了空间信息(Gevers et al., 2005; Nuerk et al., 2005)。已有的研究从多个角度验证了SNARC效应的存在。但SNARC效应灵活多变, 受到不同操控因素的影响(Dehaene et al., 1993; van Dijck & Fias, 2011)。与此同时, 关于SNARC效应发生阶段的灵活定位(刺激表征阶段还是反应选择阶段)也一直存在争论。本综述总结并对比了前期关于SNARC效应产生的几个理论假说和相关模型, 提出了SNARC效应的双阶段加工模型, 即SNARC效应的产生过程有数量信息的空间表征、数量的空间表征到反应选择两个关键阶段, 对应信息加工过程中的早期刺激表征阶段和晚期反应选择阶段。双阶段加工模型认为, 不同的操控因素从不同角度干扰SNARC效应产生的这两个阶段, 从而在不同研究中观察到SNARC效应灵活变化的现象。

5.2 展望

SNARC效应研究领域有以下问题值得进一步探索：

第一, 考察不同任务的差异。诱发SNARC效应的常用任务有数字奇偶判断任务和数字大小比较任务, 二者对于数量信息的加工不同(见图1)。在奇偶判断任务中, SNARC效应由任务无关的数量信息被自动加工表征, 产生空间编码并进一步影响反应选择而产生。而在大小比较任务中, 数量信息作为任务相关信息被加工表征, 产生空间编码并进一步影响反应选择产生SNARC效应。SNARC效应的内在产生过程在两种任务中有所区别。Nan等人通过结合SNARC、Simon和Stroop三种效应的设计发现：在奇偶判断任务中, SNARC效应只和Simon效应发生交互(Yan et al., 2021); 而在大小比较任务中, SNARC既与Simon交互, 又与Stroop交互(Nan et al., 2021)。未来可围绕两种任务的异同做进一步探索。

第二, SNARC效应的发生阶段。尽管已经有很多研究探讨了它的发生阶段, 但仍存在分歧, 并没有足够的实证研究能够解决以往研究分歧的问题。本文结合近几年的实证研究证据, 提出了双阶段加工阶段模型, 认为SNARC效应既发生在早期的刺激表征阶段又发生在晚期的反应选择阶段。SNARC效应的产生可以分为数量信息的空间表征阶段和数量的空间表征到反应选择阶段, 任何因素对其中一个阶段进行干扰就会影响SNARC效应。未来可以引入更多干扰因素来验证这个模型：(1)改变输入信息的负载强度(魏萍, 周晓林, 2005)以提高或者降低数字刺激表征的认知负荷, 如给刺激加入颜色信息来提高表征负荷; (2)提高或降低反应选择的认知负荷, 如把双按键改成四个按键提高反应维度。(3)类比与Simon效应的结合, 可以进一步与其他冲突任务结合, 引入发生在不同阶段的效应来验证模型(Kornblum et al., 1990), 如同时发生在刺激表征和反应选择的Flanker效应或Stroop效应(唐丹丹等, 2020; 唐丹丹等, 2018; Treccani et al., 2009)。(4)除采用加因素法则观察不同冲突间的交互作用之外, 引入如冲突适应(Yang et al., 2017)、比例一致性效应(Spinelli & Lupker, 2020)等其他的验证方法, 可以从更多角度考察SNARC效应与其他冲突效应(如Stroop效应、Simon效应)之间的关系。

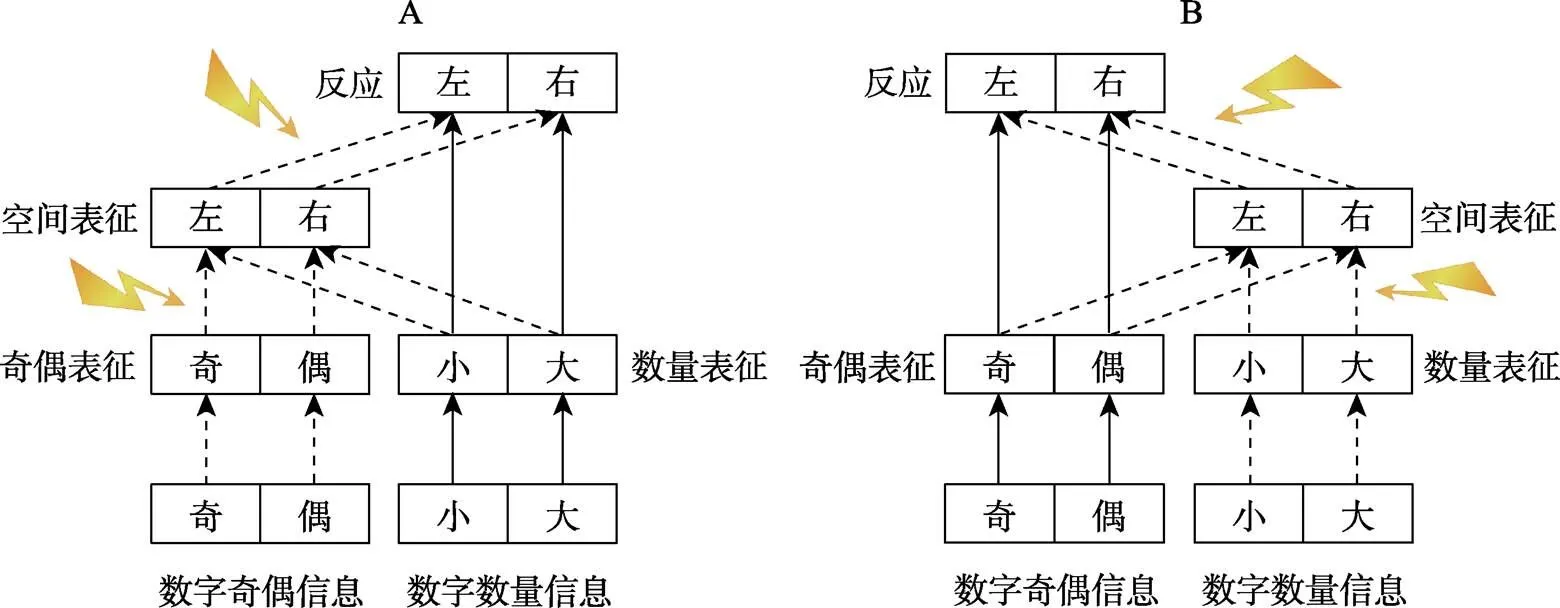
图2 不同任务中MARC效应和SNARC效应结合的双阶段加工模型。图A表示大小比较任务, 数量信息为任务相关信息; 图B表示奇偶判断任务, 奇偶信息为任务相关信息。

第三, SNARC效应与反应编码显著性效应(Linguistic Markedness of Response Codes, MARC)的关系。数字包含数量信息, 也包含奇偶信息。以往研究发现判断奇偶性质会产生与SNARC效应相似的MARC效应：左手对奇数反应更快, 右手对偶数反应更快(Nuerk et al., 2004)。与SNARC效应相似, MARC效应也可被双阶段加工模型分离成两个加工阶段(如图2)。如果引入两个阶段的干扰因素, 同样可能会观察到MARC效应的变化。数字在奇偶表征和大小表征上可能存在相互影响, 并且两者表征强度也可能存在差异。在图2中, MARC效应和SNARC效应并不是独立存在的, 二者共享了空间表征到反应选择过程。未来可着眼于MARC效应的加工过程的分离及是否符合双阶段模型, 同时也对比MARC效应与SNARC效应的关系, 进一步探究数字空间联结灵活性的内在机制。

第四, 关于工作记忆与长时记忆在SNARC效应产生原因上的争议。长时记忆和工作记忆的关系一直是研究热点, Oberauer等人(2017)认为长时记忆和工作记忆信息交换由阀门来控制, 该阀门保护工作记忆的内容不受干扰, 但当长时记忆被使用时也可以接收长时记忆信息。早期大量研究认为是阅读和文化因素引起了SNARC效应, 即数字和空间的联结来源于长时记忆表征(Dehaene et al., 1993; Fischer & Shaki, 2014; Ginsburg & Gevers, 2015; Shaki et al., 2009; Toomarian & Hubbard, 2018)。另一些研究者则认为在工作记忆中数字序列位置形成了短时空间联结才是关键(Fias & van Dijck, 2016; Fischer & Shaki, 2016; van Dijck & Fias, 2011; van Dijck et al., 2009)。Abrahamse等人(2016)等人通过理论分析长时记忆与工作记忆的相关研究, 否认了长时记忆对数字空间联结起作用, 认为只有工作记忆在其中起作用。未来还需要更多实证研究探究长时记忆与短时记忆是否同时作用于数字空间的联结, 以及二者作用的阶段是否不同。

第五, SNARC效应的神经机制。Gut等人(2012)在N1成分上观察到SNARC效应, 认为SNARC效应发生在早期; 而Keus等人(2005)与Gevers等人(2006)发现LRP在刺激锁时一致条件比不一致条件的起始潜伏期显著更早, 而反应锁时无显著差异, 认为SNARC效应发生在晚期。除此之外, 在新生儿(Di Giorgio et al., 2019)和动物(Drucker & Brannon, 2014)等无语言能力的群体中发现了数字空间联结, 引起研究者们探究生物学方面的解释(Felisatti et al., 2020; Vallortigara, 2017)。而对于SNARC效应与其他效应的关系目前更多还是集中在行为实验(Mapelli et al., 2003; Nuerk et al., 2004), 未来可利用脑电、fMRI、fNIRS等技术与生物学因素更深入地在神经机制层面上进行研究, 定位数字加工的特殊脑区以及相关的功能连接, 进一步确定灵活性的内在神经机制。

邓之君, 吴慧中, 陈英和. (2017). 数字空间联结的工作记忆机制.(9), 1492–1502.

韩萌, 毛新瑞, 蔡梦彤, 贾茜, 郭春彦. (2017). 大小判断任务中正负号及其异同对SNARC效应的影响.(8), 995–1008.

胡林成, 熊哲宏. (2011). 刺激模拟量的空间表征: 面积和亮度的类SNARC效应.(1), 58–62.

金桂春, 王有智, 王丽. (2017). Simon效应对空间-数字反应编码联合效应的抑制作用.(4), 489–494.

康武, 杨敏, 王丽平. (2013). SNARC效应:现状、理论及建议.(5), 1242–1248.

李雅君, 刘阳, 闻素霞. (2018). 书写习惯对数字空间表征SNARC效应的影响.(5), 618–623.

刘雍江, 左全顺, 郭增辉, 李慧如, 韦磐石. (2018). 贵州少数民族儿童青少年SNARC效应的发展.(5), 116–122.

乔福强, 张恩涛, 陈功香. (2016). 情境对序数的空间表征之影响.(3), 566–572.

司继伟, 周超, 张传花, 仲蕾蕾. (2013). 不同加工深度非符号数量信息的SNARC效应：眼动证据.,(1), 11–22.

孙玉, 司继伟, 黄碧娟. (2016). 分数的数量表征.(8), 1207–1216.

唐丹丹, 陈安涛, 李红, 朱海. (2020). 前额叶神经振荡活动反映了稳固的刺激冲突和反应冲突.(1), 23–32.

唐丹丹, 彭微微, 杨青松, 陈安涛, 陈雪飞. (2018). 刺激冲突和反应冲突的事件相关电位特征：中顶部P3.(1), 31–36.

王力, 张栎文, 张明亮, 陈安涛. (2012). 视觉运动Simon效应和认知Simon效应的影响因素及机制.(5), 662–671.

魏萍, 周晓林. (2005). 从知觉负载理论来理解选择性注意.(4), 413–420.

徐晓东, 刘昌. (2006). 数字的空间特性.(6), 851–858.

Abrahamse, E., van Dijck, J. P., & Fias, W. (2016). How does working memory enable number-induced spatial biases?, 977.

Bächtold, D., Baumüller, M., & Brugger, P. (1998). Stimulus- response compatibility in representational space.(8), 731–735.

Brysbaert, M. (1995). Arabic number reading: On the nature of the numerical scale and the origin of phonological recoding.(4), 434–452.

Bulf, H., de Hevia, M. D., & Macchi Cassia, V. (2016). Small on the left, large on the right: Numbers orient visual attention onto space in preverbal infants.(3), 394–401.

Chen, Q., & Verguts, T. (2010). Beyond the mental number line: A neural network model of number-space interactions.(3), 218–240.

Cohen, Kadosh, R., & Walsh., V. (2009). Numerical representationin the parietal lobes: Abstract or not abstract?313–328.

Cutini, S., Scarpa, F., Scatturin, P., Dell'Acqua, R., & Zorzi, M. (2014). Number-space interactions in the human parietal cortex: Enlightening the SNARC effect with functional near-infrared spectroscopy.(2), 444–451.

Daar, M., & Pratt, J. (2008). Digits affect actions: the SNARC effect and response selection.(4), 400–405.

Dehaene, S. (1989). The psychophysics of numerical comparison: A reexamination of apparently incompatible data.,(6), 557–566.

Dehaene, S. (1992). Varieties of numerical abilities.(1-2), 1–42.

Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude.(3), 371–396.

Dehaene, S., Dupoux, E., & Mehler, J. (1990). Is numerical comparison digital? Analogical and symbolic effects in two-digit number comparison.(3), 626–641.

Dehaene, S., Molko, N., Cohen, L., & Wilson, A. J. (2004). Arithmetic and the brain.(2), 218–224.

De Jong, R., Liang, C.-C., & Lauber, E. (1994). Conditional and unconditional automaticity: A dual-process model of effects of spatial stimulus-response correspondence.(4), 731–750.

Deng, Z. J., Chen, Y. H., Zhang, M., Li, Y. J., & Zhu, X. S. (2018). The association of number and space under different tasks: Insight from a process perspective, 957.

Deng, Z. J., Chen, Y. H., Zhu, X. S., & Li, Y. J. (2017). The effect of working memory load on the SNARC effect: Maybe tasks have a word to say.(3), 428–441.

Didino, D., Breil, C., & Knops, A. (2019). The influence of semantic processing and response latency on the SNARC effect., 75–86.

Drucker, C. B., & Brannon, E. M. (2014). Rhesus monkeysmap number onto space.(1), 57–67.

Duncan, J. (1980). The locus of interference in the perception of simultaneous stimuli.(3), 272–300.

Felisatti, A., Laubrock, J., Shaki, S., & Fischer, M. H. (2020). A biological foundation for spatial-numerical associations: The brain's asymmetric frequency tuning.(1), 44–53.

Fias, W., Brysbaert, M., Geypens, F., & d'Ydewalle, G. (1996). The Importance of Magnitude Information in Numerical Processing: Evidence from the SNARC Effect.(1), 95–110.

Fias, W., & van Dijck, J. P. (2016). The temporary nature of number-space interactions.(1), 33–40.

Fischer, M. H., Mills, R. A., & Shaki, S. (2010). How to cook a SNARC: Number placement in text rapidly changes spatial-numerical associations.(3), 333–336.

Fischer, M. H., & Shaki, S. (2014). Spatial associations in numerical cognition--from single digits to arithmetic.(8), 1461–1483.

Fischer, M. H., & Shaki, S. (2016). Measuring spatial-numerical associations: Evidence for a purely conceptual link.(1), 109–112.

Fischer, M. H., Warlop, N., Hill, R. L., & Fias, W. (2004). Oculomotor bias induced by number perception.(2), 91–97.

Fitousi, D., & Algom, D. (2020). A model for two-digit number processing based on a joint Garner and system factorial technology analysis.(4), 676–700.

Fumarola, A., Prpic, V., Da Pos, O., Murgia, M., Umiltà, C., & Agostini, T. (2014). Automatic spatial association for luminance.(3), 759–765.

Galton, F. (1880). Visualised numerals.252–256.

Gevers, W., Caessens, B., & Fias, W. (2005). Towards a common processing architecture underlying Simon and SNARC effects.(5), 659–673.

Gevers, W., Lammertyn, J., Notebaert, W., Verguts, T., & Fias, W. (2006). Automatic response activation of implicit spatial information: Evidence from the SNARC effect.(3), 221–233.

Gevers, W., Ratinckx, E., De Baene, W., & Fias, W. (2006). Further evidence that the SNARC effect is processed along a dual-route architecture: Evidence from the lateralized readiness potential.(1), 58–68.

Gevers, W., Reynvoet, B., & Fias, W. (2003). The mental representation of ordinal sequences is spatially organized.(3), B87–B95.

Gevers, W., Santens, S., Dhooge, E., Chen, Q., Van den Bossche, L., Fias, W., & Verguts, T. (2010). Verbal-spatial and visuospatial coding of number-space interactions.(1), 180–190.

Gevers, W., Verguts, T., Reynvoet, B., Caessens, B., & Fias, W. (2006). Numbers and space: a computational model of the SNARC effect.(1), 32–44.

Ginsburg, V., & Gevers, W. (2015). Spatial coding of ordinal information in short- and long-term memory.(8), 8.

Giorgio, E. D., Lunghi, M., Rugani, R., Regolin, L., Dalla Barba, B., Vallortigara, G., & Simion, F. (2019). A mental number line in human newborns.(6), e12801.

Gut, M., Szumska, I., Wasilewska, M., & Jaskowśki, P. (2012). Are low and high number magnitudes processed differently while resolving the conflict evoked by the SNARC effect?(1), 7–16.

Hartmann, M., Gashaj, V., Stahnke, A., & Mast, F. W. (2014). There is more than "more is up": Hand and foot responses reverse the vertical association of number magnitudes.(4), 1401–1414.

He, D. X., He, X. Y., Zhao, T. T., Wang, J., Li, L. Z., & Louwerse, M. (2020). Does Number Perception Cause Automatic Shifts of Spatial Attention? A Study of the Att-SNARC Effect in Numbers and Chinese Months., 680.

Herrera, A., Macizo, P., & Semenza, C. (2008). The role of working memory in the association between number magnitude and space.(2), 225–237.

Hirsch, P., Nolden, S., & Koch, I. (2017). Higher-order cognitive control in dual tasks: Evidence from task-pair switching.(3), 569–580.

Hung, Y. H., Hung, D. L., Tzeng, O. J.-L., & Wu, D. H. (2008). Flexible spatial mapping of different notations of numbers in Chinese readers.(3), 1441–1450.

Ito, Y., & Hatta, T. (2004). Spatial structure of quantitative representation of numbers: Evidence from the SNARC effect.(4), 662–673.

Keus, I. M., Jenks, K. M., & Schwarz, W. (2005). Psychophysiological evidence that the SNARC effect has its functional locus in a response selection stage.(1), 48–56.

Keus, I. M., & Schwarz, W. (2005). Searching for the functional locus of the SNARC effect: Evidence for a response-related origin.(4), 681–695.

Kong, F., Zhao, J. J., & You, X. Q. (2012). Components representation of negative numbers: Evidence from auditory stimuli detection and number classification tasks.(4), 691–701.

Kornblum, S., Hasbroucq, T., & Osman, A. (1990). Dimensional overlap: Cognitive basis for stimulus-response compatibility--A model and taxonomy.(2), 253–270.

Krause, F., Lindemann, O., Toni, I., & Bekkering, H. (2014). Different brains process numbers differently: Structural bases of individual differences in spatial and nonspatial number representations.(4), 768–776.

Leuthold, H. (2011). The Simon effect in cognitive electrophysiology: A short review.(2), 203–211.

Li, Q., Nan, W. Z., Wang, K., & Liu, X. (2014). Independent processing of stimulus-stimulus and stimulus-response conflicts.(2), e89249.

Lindemann, O., Abolafia, J. M., Pratt, J., & Bekkering, H. (2008). Coding strategies in number space: Memory requirements influence spatial-numerical associations.(4), 515–524.

Liu, X., Park, Y., Gu, X. S., & Fan, J. (2010). Dimensional overlap accounts for independence and integration of stimulus-response compatibility effects.(6), 1710–1720.

Lonnemann, J., Linkersdorfer, J., Nagler, T., Hasselhorn, M., & Lindberg, S. (2013). Spatial representations of numbers and letters in children., 544.

Mapelli, D., Rusconi, E., & Umiltà, C. (2003). The SNARC effect: An instance of the Simon effect?(3), B1–B10.

Marois, R., Larson, J. M., Chun, M. M., & Shima, D. (2006). Response-specific sources of dual-task interference in human pre-motor cortex.(6), 436–447.

Moro, S. B., Dell'Acqua, R., & Cutini, S. (2018). The SNARC effect is not a unitary phenomenon.(2), 688–695.

Moyer, R. S., & Landauer, T. K. (1967). Time required for judgements of numerical inequality., 1519–1520.

Müller, D., & Schwarz, W. (2007). Exploring the mental number line: Evidence from a dual-task paradigm.(5), 598–613.

Myachykov, A., Cangelosi, A., Ellis, R., & Fischer, M. H. (2015). The oculomotor resonance effect in spatial-numerical mapping., 162–169.

Nan, W. Z., Yan, L. Z., Yang, G. C., Liu, X., & Fu, S. M. (2021). Two processing stages of the SNARC effect.. doi: 10.1007/s00426-021-01506-5

Nuerk, H. C., Iversen, W., & Willmes, K. (2004). Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect.(5), 835–863.

Nuerk, H. C., Wood, G., & Willmes, K. (2005). The universal SNARC effect: The association between number magnitude and space is amodal.(3), 187–194.

Oberauer, K., Awh, E., & Sutterer, D. W. (2017). The role of long-term memory in a test of visual working memory: Proactive facilitation but no proactive interference.(1), 1–22.

Pinto, M., Pellegrino, M., Marson, F., Lasaponara, S., & Doricchi, F. (2019). Reconstructing the origins of the space-number association: Spatial and number-magnitude codes must be used jointly to elicit spatially organised mental number lines., 143–156.

Prado, J., Van der Henst, J. B., & Noveck, I. A. (2008). Spatial associations in relational reasoning: Evidence for a SNARC-like effect.(8), 1143–1150.

Pressigout, A., Charvillat, A., Mersad, K., & Doré-Mazars, K. (2019). Time dependency of the SNARC effect for different number formats: Evidence from saccadic responses.(7), 1485–1495.

Proctor, R. W., & Cho, Y. S. (2006). Polarity correspondence: A general principle for performance of speeded binary classification tasks.(3), 416–442.

Prpic, V., Fumarola, A., De Tommaso, M., Luccio, R., Murgia, M., & Agostini, T. (2016). Separate mechanisms for magnitude and order processing in the spatial-numerical association of response codes (SNARC) effect: The strange case of musical note values.(8), 1241–1251.

Ratinckx, E., & Brysbaert, M. (2002). Interhemispheric stroop-like interference in number comparison: Evidence for strong interhemispheric integration of semantic number information.(2), 217–229.

Riello, M., & Rusconi, E. (2011). Unimanual SNARC Effect: Hand Matters., 372.

Rusconi, E., Bueti, D., Walsh, V., & Butterworth, B. (2011). Contribution of frontal cortex to the spatial representation of number.(1), 2–13.

Scerrati, E., Lugli, L., Nicoletti, R., & Umiltà, C. (2017). Comparing Stroop-like and Simon Effects on Perceptual Features.(1), 17815.

Schuller, A.-M., Hoffmann, D., Goffaux, V., & Schiltz, C. (2014). Shifts of spatial attention cued by irrelevant numbers: Electrophysiological evidence from a target discrimination task.(4), 442–458.

Schwarz, W., & Keus, I. M. (2004). Moving the eyes along the mental number line: Comparing SNARC effects with saccadic and manual responses.(4), 651–664.

Seron, X., Pesenti, M., Noël, M. P., Deloche, G., & Cornet, J. A. (1992). Images of numbers, or “When 98 is upper left and 6 sky blue”.(1-2), 159–196.

Shaki, S., Fischer, M. H., & Petrusic, W. M. (2009). Reading habits for both words and numbers contribute to the SNARC effect.(2), 328–331.

Shaki, S., & Gevers, W. (2011). Cultural Characteristics Dissociate Magnitude and Ordinal Information Processing.(4), 639–650.

Spinelli, G., & Lupker, S. J. (2020). Item-specific control of attention in the stroop task: Contingency learning is not the whole story in the item-specific proportion-congruent effect.(3), 426–435.

Sternberg, S. (1969). The discovery of processing stages: Extensions of Donders' method., 276–315.

Stroop, J. R. (1935). Studies of interference in serial verbal reactions.(6), 643–662.

Tlauka, M. (2002). Switching imagined viewpoints: the effects of viewing angle and layout size.(2), 193–201.

Tombu, M. N., Asplund, C. L., Dux, P. E., Godwin, D., Martin, J. W., & Marois, R. (2011). A Unified attentional bottleneck in the human brain.(33), 13426–13431.

Toomarian, E. Y., & Hubbard, E. M. (2018). On the genesis of spatial-numerical associations: Evolutionary and cultural factors co-construct the mental number line., 184–199.

Treccani, B., Cubelli, R., Della Sala, S., & Umiltà, C. (2009). Flanker and Simon effects interact at the response selectionstage.(9), 1784–1804.

Treccani, B., Milanese, N., & Umilta, C. (2010). Influence on Simon and SNARC effects of a nonspatial stimulus- response mapping: Between-task logical recoding.(5), 1239–1254.

Tschentscher, N., Hauk, O., Fischer, M. H., & Pulvermuller, F. (2012). You can count on the motor cortex: Finger counting habits modulate motor cortex activation evoked by numbers.(4), 3139–3148.

Vallortigara, G. (2017). Comparative cognition of number and space: The case of geometry and of the mental number line.(1740), 20170120.

van Dijck, J. P., & Fias, W. (2011). A working memory account for spatial-numerical associations.(1), 114–119.

van Dijck, J. P., Gevers, W., & Fias, W. (2009). Numbers are associated with different types of spatial information depending on the task.(2), 248–253.

van Galen, M. S., & Reitsma, P. (2008). Developing access to number magnitude: A study of the SNARC effect in 7- to 9-year-olds.(2), 99–113.

van Opstal, F., & Verguts, T. (2011). The origins of the numerical distance effect: The same-different task.(1), 112–120.

Verguts, T., Fias, W., & Stevens, M. (2005). A model of exact small-number representation.(1), 66–80.

Viarouge, A., Hubbard, E. M., & Dehaene, S. (2014). The organization of spatial reference frames involved in the SNARC effect.(8), 1484–1499.

Vu, K.-P. L., & Proctor, R. W. (2001). Determinants of right-left and top-bottom prevalence for two-dimensional spatial compatibility.(4), 813–828.

Wang, X. T., Du, F., He, X. S., & Zhang, K. (2014). Enhanced spatial stimulus-response mapping near the hands: The Simon effect is modulated by hand-stimulus proximity.(6), 2252–2265.

Weis, T., Estner, B., Krick, C. M., Reith, W., & Lachmann, T. (2015). SNARC meets SPARC in fMRI--Interdependence of compatibility effects depends on semantic content., 331–338.

Weis, T., Estner, B., van Leeuwen, C., & Lachmann, T. (2016). SNARC (spatial-numerical association of response codes) meets SPARC (spatial-pitch association of response codes): Automaticity and interdependency in compatibility effects.(7), 1366–1383.

Wiegand, K., & Wascher, E. (2005). Dynamic aspects of stimulus-response correspondence: Evidence for two mechanisms involved in the Simon effect.(3), 453–464.

Wiegand, K., & Wascher, E. (2007). Response coding in the Simon task.(4), 401–410.

Yan, L. Z., Yang, G. C., Nan, W. Z., Liu, X., & Fu, S. M. (2021). The SNARC effect occurs in the response-selection stage., 103292.

Yang, G. C., Nan, W. Z., Zheng, Y., Wu, H. Y., Li, Q., & Liu, X. (2017). Distinct cognitive control mechanisms as revealed by modality-specific conflict adaptation effects.(4), 807–818.

Zhang, P., Cao, B. H., & Li, F. H. (2020). SNARC effect modulated by central executive control: revealed in a cue-based trisection task.. https:// doi.org/10.1007/s00426-020-01407-z

Zhao, T. T., He, X. Y., Zhao, X. R., Huang, J. R., Zhang, W., Wu, S., & Chen, Q. (2018). The influence of time units on the flexibility of the spatial numerical association of response codes effect.(2), 299–320.

Zhou, D. D., Luo, J., Yi, Z. Z., Li, Y., Yang, S. T., Verguts, T., & Chen, Q. (2020). The hand-lateralization of spatial associations in working memory and long-term memory.(8), 1150–1161.

Zorzi, M., Priftis, K., & Umiltà, C. (2002). Neglect disrupts the mental number line., 138–139

The flexibility of spatial-numerical associations and its internal mechanism

YAN Lizhu1, CHEN Yanxiu1, LIU Xun2, FU Shimin1, NAN Weizhi1

(1Department of Psychology and Center for Brain and Cognitive Sciences, School of Education, Guangzhou University, Guangzhou 510006, China)(2CAS Key Laboratory of Behavioral Science, Institute of Psychology, 16 Lincui Road, Chaoyang District, Beijing 100101, China)

Spatial-numerical associations (SNAs) are a hot topic in the field of cognitive psychology. An important index to explore SNAs is the spatial-numerical association of response codes (SNARC) effect (i.e., faster responses to small numbers using left effectors, and the inverse for large numbers). Previous studies have verified the universality of the SNARC effect and its flexibility in direction, and a variety of theoretical explanations have been proposed. In addition, the SNARC effect is also flexible in the processing stage at which it occurs, which might be caused by: (1) disparities in the comprehension of additive-factor logic, (2) observation from a single point, (3) different types of Simon effects were adopted as the measure index, and (4) different tasks were adopted. Combining the above reasons, a new two-stage processing (spatial representation of magnitude, spatial representation to response selection) model was proposed. It was proposed that different interference factors acting on the two stages might be the core reason for the flexibility of the SNARC effect. Future research could focus on comparisons of different tasks and the adoption of various interference factors to verify the two-stage processing model and combine cognitive neuroscience technologies to further elucidate the neural mechanism underlying the flexibility of SNAs.

SNARC effect, flexibility, spatial-numerical associations, two-stage processing model

B842

2021-04-10

* 国家自然科学基金面上项目(31970993); 广东省哲学社科共建项目(GD17XXL03); 教育部人文社科青年项目(19YJC190017)。

南威治, E-mail: nanwz@gzhu.edu.cn