高中数学试题中的“思政元素”探析

海南 张 维

《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课程标准》)中明确指出：数学课程要以学生发展为本，落实立德树人的根本任务，培育科学精神和创新意识，提升数学学科核心素养.基于此，将立德树人融入日常教学中，切实践行“课程思政”理念无疑是数学课程教学义不容辞的责任.在日常的教育教学实践中，要求教师在教学中引导学生学习数学学科基础知识，发展数学能力的同时，结合数学学科本身的特点，寻找和挖掘蕴含其中的丰富的“思政元素”，对学生进行思政教育，实现数学知识学习、数学技能训练与情感、态度、价值观培育的“同向同行”，以达到“润物细无声”的育人效果.解题是数学教与学中的核心实践行为，因此“试题”也就成了“思政元素”藉以蕴藏的极其重要的“富矿”.本文拟对高中数学试题中常见的“思政元素”进行具体分析，以期对高中数学“课程思政”的顺利推进有所裨益.

高中数学试题中的“思政元素”主要包含如下四类：

一、 体现我国古代先进的科技成果和辉煌的数学、文学成就的元素

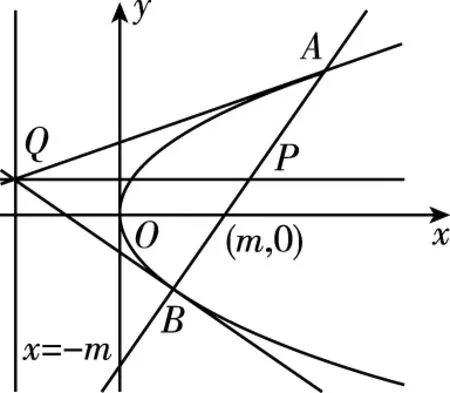
【例1】日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为

( )

A.20° B.40° C.50° D.90°

【答案】B

很显然，从“课程思政”着眼，在解题指导的实践中，本题中的“日晷”有特别介绍的必要.介绍其“简历”，能让学生明白日晷是人类在漫长的历史长河中探索世界、科技创新的创造物，它涵盖了几何学、算术、光学、天文学等学科，说明了人类用他们的勤劳和智慧不断探索着现实世界事物的客观规律及其内在联系.同时，日晷作为古代计时仪器在历史上的影响十分深远，现代人更赋予其珍惜时间、拼搏向上的含义.此外，日晷指天接地的形象容易让人想起中国文化中先贤“天行健，君子以自强不息；地势坤，君子以厚德载物”的谆谆教诲.如此一来，以传统文化作为试题背景不仅更容易激发学生的学习兴趣，还使得试题具有更丰富的育人价值，能很好地落实数学学科育人的本质要求.

再如，中国悠久的历史中，取得突出成就的数学家为数不少.他们的姓名越来越频繁地出现在相关试题中，特别是新时期的高考试题中，如秦九韶、杨辉、朱世杰直至现代的陈景润等.这类试题体现了对数学的文化价值和对古代数学家研究成果的尊重，能让学生体会数学家的创新和探索精神，于潜移默化中接受数学文化的熏陶，帮助学生养成严谨求真、锲而不舍的科学精神，是对学生进行思政教育的良好内容.

当试题中出现这些数学家事迹时，教师应该适当的介绍一些他们的逸闻趣事，这些内容学生一般了解不多，但其实他们很感兴趣.有些老师为了追求讲题效率，直接跳过概述部分，来到题目的正文，殊不知通过对这些知识的适度介绍，不仅能拓展学生的知识面，更能提升其课程学习的兴趣，从而达到事半功倍的教育教学效果.

不仅数学家及其成就在试题中被屡屡提及，灿烂的中国文学成就也日渐成为数学试题中闪亮的点缀，这样的“点缀”同样可以成为很好的“思政元素”.

【例3】《红楼梦》 《三国演义》 《西游记》和《水浒传》是中国古典文学瑰宝，并称为中国古典小说四大名著.某中学语文组为了解本校学生阅读四大名著的情况，对100名同学进行随机抽样调查，其中阅读过《三国演义》或《水浒传》的同学共有80名，阅读过《水浒传》的同学有70名，《三国演义》与《水浒传》都阅读过的同学有50名，则我校阅读过《三国演义》的学生人数与该校学生总数比值的估计值为.

【答案】0.6

这样的试题，教师要借机问学生对中国古代文学作品阅读了多少，了解多少中国古代文人雅士，只需教师几句简单的提示语，就可能成为在潜移默化中激发学生对中华辉煌文学成就的兴趣及自豪感的良好“思政元素”.

二、反映新时期国家科技日新月异的元素

例如，涉及“新四大发明”的题目.

【例4】近年来，我国交通发展迅速，特别是高铁，技术先进.假如，经停某站的高铁列车共有40车次，正点率为0.97的有10个车次，正点率为0.98的有20个车次，正点率为0.99的有10个车次，则经停该站高铁列车所有车次的平均正点率的估计值为.

【答案】0.98

本题用简洁的语言介绍我国“高铁”建设所取得的举世瞩目的成就，在教学中，结合相关背景介绍，这就可以是一个不错的“思政元素”.例如，“十三五”以来，国家努力改善交通、住房、医疗、教育等，使得多个城市实现了1小时或半小时经济圈与生活圈，让人民幸福感与获得感不断增强.由于交通等发展迅速，在世界上获得了“基建狂魔”称号，与此同时带动了工业、科技等的发展，实现了多个领域的“弯道超车”.如此的背景与试题中的“元素”结合起来，只需教师自觉地稍加引导，在上好数学“大课”的同时，无疑可以成就一堂极好的思政“微课”.

【例5】李明自主创业，除了开一个实体店售卖水果外,还在网上售卖水果，网上销售的水果中有莲雾、龙眼、荔枝、菠萝，价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元．每笔订单顾客网上支付成功后，李明会得到支付款的80%．

①当x=10时，顾客一次购买莲雾和荔枝各1盒，需要支付元；

②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为．

【答案】130;15

本题联系学生身边的现实生活，考查其运用数学知识与技能解决实际问题的能力.同时，体现了互联网科技的发展给予普通人谋生手段的拓展以及生活质量提升的意义，人们不再是远走他乡去打工，在自家利用自产就可以实现远销，既可以解决留守家庭的问题，又能实现果农与消费者面对面，打通了消费渠道.

【例6】随着互联网时代的到来，人们的支付方式发生了很大转变，移动支付和网上支付已经走入人们的日常生活.为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校学生中随机抽取了100人，发现样本中A与B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额(元)支付方式(0,1000](1000,2000]大于2000仅使用A18人9人3人仅使用B10人14人1人

(1)从全校学生中随机抽取1人，估计该学生上个月A与B两种支付方式都使用的概率；

(2)从样本中仅使用A和仅使用B的学生中各随机抽取1人，以X表示这2人中上个月支付金额大于1 000元的人数，求X的分布列和数学期望.

(2)x的分布列为

X012P6251325625

E(X)=1

本题考查数学推理能力和运算求解能力，而其中蕴含的“思政元素”可以让学生从支付方式的变革中感受到科技发展给生活带来的极大的便利，有利于增强其对国家和个人未来的希望和信心.特别是我国已经开始实行数字货币，将成为一次新的变革，这种变革对于推动人民币国际化和有效应对美国的金融遏制都具有重要意义.这样的“思政元素”很明显是非常亮眼的，在实践中也无疑是非常有效的.

三、 反映中国特色社会主义制度优越性的元素

例如，脱贫攻坚与新农村建设成果，“以人为本”“人民至上”的施政纲领，“绿水青山就是金山银山”的发展理念，等等.

【例7】为实现有效利用扶贫资金，增加贫困村民收入，扶贫工作组结合某贫困村水质优良的特点，决定利用扶贫资金从外地购买甲、乙、丙三种鱼苗在鱼塘中进行养殖试验，试验后选择其中一种进行大面积养殖，已知鱼苗甲的自然成活率为0.8，鱼苗乙、丙的自然成活率均为0.9，且甲、乙、丙三种鱼苗是否成活相互独立.

(1)试验时从甲、乙、丙三种鱼苗中各取一尾，记自然成活的尾数为X，求X的分布列和数学期望；

(2)试验后发现乙种鱼苗较好，扶贫工作组决定购买n尾乙种鱼苗进行大面积养殖，为提高鱼苗的成活率，工作组采取增氧措施，该措施实施对能够自然成活的鱼苗不产生影响，使不能自然成活的鱼苗的成活率提高了50%，若每尾乙种鱼苗最终成活后可获利10元，不成活则亏损2元，且扶贫工作组的扶贫目标是获利不低于37.6万元，问至少需购买多少尾乙种鱼苗？

【答案】(1)x的分布列为

X0123P0.0020.0440.3060.648

E(X)=2.6;

(2)40 000尾

2020年中国实现了9 000多万人口的脱贫攻坚任务，现在又在向乡村振兴这一目标出发，因此这类试题更加富有浓郁的时代与生活气息，其中所蕴含的“思政元素”也更加亮眼.

四、美育、体育和劳育元素

【例8】北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层，上层中心有一块圆形石板(称为天心石)，环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，已知每层环数相同，且下层比中层多729块，则三层共有扇面形石板(不含天心石)

( )

A.3 699块 B.3 474块

C.3 402块 D.3 339块

【答案】C

本题主要考查与等差数列前n项和有关的计算问题，是一道难度不大的题，而其中蕴含着的“思政元素”却值得注意：圜丘专用于祭天，其构件数量全部采用“9”，象征九重天.中国传统文化中极其重要的一些思想理念就这样在建筑上鲜明地体现了出来，这不仅体现了古人的设计之精心和安排之巧妙，还体现了丰富的数学文化之美！只需稍加提示，就能够让学生体验数学在建筑学中应用的同时，切实感受到祖先智慧的伟大！

包含体育和劳育等元素的试题同样很多，此处不再赘述.