基于壁面电势诊断霍尔推力器的振荡特性
陈 杰,康小录,赵 震
(1.上海空间推进研究所,上海 201112;2.上海空间发动机工程技术研究中心,上海 201112)
0 引 言
霍尔推力器是一种通过霍尔效应电离工质并利用静电场加速离子产生推力的动力装置,主要应用于航天器的轨道维持和姿态控制等任务[1-3]。霍尔推力器工作时,中性原子和带电粒子在复杂电磁场中的运动产生了多种等离子体振荡。图1给出了霍尔推力器典型的振荡模式。等离子体振荡不但会影响霍尔推力器的稳定工作(低频段),其电磁辐射还有可能干扰航天器上其它设备的正常运行(高频段),因而振荡现象一直是霍尔推力器的主要研究方向之一。
按照频谱范围,霍尔推力器中的振荡可以分为低频振荡、高频振荡和超高频振荡。依据不同振荡模式的特征,需要采用不同的测量方法。当前研究霍尔推力器振荡现象的方法主要有理论分析、实验测量和数值仿真。其中,实验测量方法主要有放电电流测量、高速摄影测量、高速探针测量和激光诱导荧光测量等[5-7]。
放电电流振荡不但是霍尔推力器工程应用中需要重点考虑的因素,也是间接研究霍尔推力器内部等离子体振荡的手段之一。放电电流的振荡是影响霍尔推力器工程应用最主要的因素之一,振荡主要来自于呼吸效应等过程,振荡的峰峰值可达放电电流平均值的一倍左右,对供电系统的影响较大。由于测量的便利性和工程应用的必要性,使得放电电流相关的低频振荡研究相对完备[8]。探针测量作为一种等离子体测量手段也被应用于霍尔推力器等离子体振荡研究,其测量能力主要受限于采集设备的响应时间。由于探针伸入放电室内部会对等离子体环境产生干扰,使得探针很难对放电室内部的振荡进行准确测量。
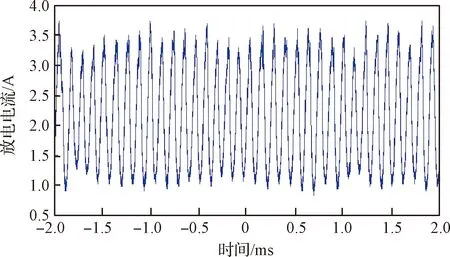
图2 实验测量的霍尔推力器等离子振荡Fig.2 Plasma oscillation of Hall thruster measured experimentally
数值仿真也是研究霍尔推力器振荡现象的主要方法之一。虽然数值仿真有利于发现推力器内部一些难以测量的振荡模式,但是霍尔推力器中等离子体运动较为复杂使得相应的仿真模型都经过较多的简化处理,计算结果与实际依旧存在差距。因此探索新的振荡测量方法对于振荡的研究显得较为必要。
随着霍尔推力器技术的发展,出现了一种具有导电壁面的霍尔推力器(如BHT-1500、BHT-8000、KM-45和KM-10等)。这种推力器的放电室壁面部分采用导电材料,部分为陶瓷材料。放电室金属材料的引入使得利用壁面电势振荡研究霍尔推力器内部振荡模式成为可能。等离子体的振荡会导致放电室内部粒子的运动速度和方向发生变化,影响等离子体与壁面之间的相互作用,从而改变推力器壁面的电势。研究壁面电势的振荡有助于了解霍尔推力器内部等离子体的振荡情况。本文通过对霍尔推力器不同工况下金属壁面与阳极之间电势差的振荡情况进行研究,得出霍尔推力器等离子体振荡与推力器工作参数的关系。
1 实验设备
实验所用的VF-4试验台具有中小功率霍尔推力器高低温实验和长寿命实验能力。真空舱直径为2.5 m,长度为6 m,氙气抽气速率达126000 L/s,极限真空度可达2×10-5Pa,千瓦级霍尔推力器额定工况(工质流量约50 sccm)点火时真空度优于7×10-3Pa。配套流量计最高精度可达0.01 sccm。推力架推力测量范围为5~1000 mN,分辨率优于0.1 mN。

图3 VF-4电推进试验台Fig.3 VF-4 Electric Propulsion Test Bench
实验所用的推力器是上海空间推进研究所新研的一款千瓦级霍尔推力器,其额定放电功率为1.35 kW,工作电压为500V,推力65 mN,比冲约2100 s。推力器采用金属-陶瓷复合放电室结构,靠近阳极区域为导电(金属)材料,出口区域保留绝缘(陶瓷)材料,推力器主要结构如图4所示。金属材料壁面的应用,使得测量放电室壁面与阳极之间的电势差(悬浮壁面没有净电流,以下未说明情况下电势均指金属放电室壁面与阳极之间的电势差)成为可能。
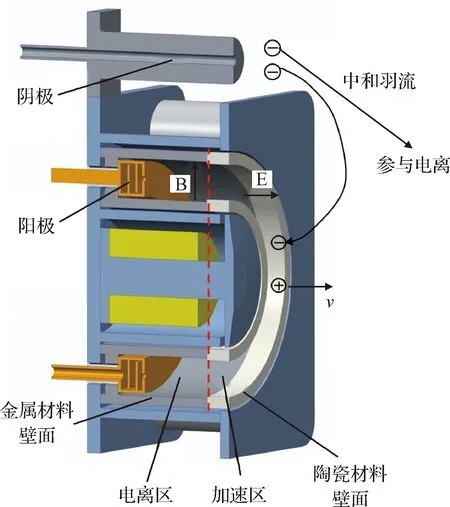
图4 金属-陶瓷复合放电室霍尔推力器主要结构Fig.4 The main structure of the Hall thruster with metal-ceramic composite discharge chamber
2 霍尔推力器电势振荡分析
霍尔推力器放电室内的等离子体在电场和磁场中运动,产生了种类丰富的振荡模式。低频振荡模式包括呼吸效应、工质电离和激发振荡、电子-离子库仑碰撞、电子-原子碰撞振荡和低混杂波等。不同振荡模式与推力器工作参数、放电室结构、放电室材料以及等离子运动情况等因素相关。研究振荡模式与推力器工作参数的关系有助于优化推力器性能,丰富相关的理论知识。
电势测量作为一种电路测量方法与放电电流测量一样也可以用于霍尔推力器振荡的研究。在霍尔电推进早期研究中,Morozov利用可移动电极在霍尔推力器内进行电势扰动实验测量[9],这种电势测量方法与现在利用探针测量振荡的方法相似。探针测量霍尔推力器振荡依旧存在很多不足。一方面霍尔推力器近场羽流和放电室内部的等离子体具有较高的能量容易损伤探针;另一方面探针靠近放电室时也会影响霍尔推力器的正常工作,从而影响测量的准确性。
实验所用的是一种新型的具有金属放电室壁面的霍尔推力器。测量金属壁面上的电势振荡不仅不需要引入测量探针,而且由于金属壁面几乎与放电室内绝大部分粒子进行相互作用,更能反映放电室内部的等离子体振荡情况。因而利用悬浮金属放电室可以克服探针测量的不足。
2.1 金属壁面电势的形成
金属壁面的等电势特性使得其等离子体鞘层与陶瓷壁面有所不同。图5给出了金属放电室鞘层电势沿轴向的分布(不考虑磁场位形的影响),以及径向鞘层电子电流密度和离子电流密度沿轴向的分布。鞘层径向电子电流集中在靠近陶瓷壁面的区域内,靠近阳极区域径向电子电流忽略不计[10]。由于放电室中电势分布的影响,使得在靠近阳极的区域与壁面电势差最大,离子电流密度达到最大值。

图5 金属壁面鞘层电势及电流密度分布Fig.5 Distribution of sheath potential and current density on metal wall
在Z=z截面处鞘层电势差可以表示为:
φs=φw-φ
(1)
式中:φs为鞘层电势;φw为金属壁面电势(金属壁面不同轴向位置电势相同);φ为Z=z处鞘层边界处电势。
推力器壁面负鞘层的电子电流密度可以表示为:
(2)
式中:je为电子电流;e为电子电量;ne为电子密度;γ为二次电子发射系数;k为波尔兹曼常数;Te为电子温度;me为电子质量。
假设鞘层与预鞘层边缘离子依旧满足Bohm判据,离子电流密度可以表示为:
(3)
式中:ji为离子电流;ni为离子密度;mi为离子质量。
在Z=z处(ni=ne=n0)存在壁面净电流密度。由于金属壁面悬浮,使得壁面鞘层总的净电流密度为零。假设金属壁面鞘层沿周向均匀,且内外壁面鞘层沿轴向分布一致。则可以通过式(2)和式(3)求出壁面电势:
(4)
式中:n0为通道中心等离子体密度;L为金属放电室区域长度;φw为待求量;n0、Te、φ均为已知量(测量得到)且与到阳极的距离有关。
金属放电室壁面靠近陶瓷的区域与加速区有重合部分,使得靠近陶瓷部分的金属壁面处等离子体电势变化较大。电子能量和电场分布类似,从阳极到放电室出口先增加再减小[11]。从以上分析可以看出,金属壁面的电势受壁面附近带电粒子运动影响,因而与放电电流振荡能够反映霍尔推力器内部振荡一样,金属壁面附近的等离子体振荡能够被金属壁面电势的振荡反映出来。
2.2 霍尔推力器典型振荡模式
2.2.1呼吸效应
呼吸效应是霍尔推力器低频振荡的主要组成部分,振荡源于工质的周期性补充和电离。这种振荡模式的振荡频率一般在10~40 kHz,振荡频率与推力器比冲呈正相关[12],可用于霍尔推力器工作参数的优化。呼吸效应振荡频率可表示为:
(5)

对于典型霍尔推力器参数(放电室内原子的平均速度为200~300 m/s;阳极比冲为1600 s;电离区和加速区的平均离子速度为9000 m/s;呼吸效应区域长度约为0.01~0.03 m),可得呼吸效应频率为7.1~26.1 kHz。在振荡频谱分析中,可根据呼吸效应频率分布找到相应的振荡模式,并通过幅值判断呼吸效应的强弱。
2.2.2周向聚集振荡
霍尔推力器放电室内由于径向磁场和轴向电场的存在,会使电子发生周向漂移运动。电子在周向运动过程中会与中性原子发生碰撞并产生电离现象。通过高速摄影方法可以发现放电室内明暗区域沿周向移动(也可以通过等离子体探针测量到某一位置周向等离子体密度变化)。电子周向聚集振荡的成因较为复杂,振荡频率约为数十kHz。振荡频率与霍尔推力器中呼吸效应和离子回旋频率相近[13]。
由于电子的这种周向聚集振荡在周向上不均匀,因而本文研究的环形金属壁面结构不能响应周向等离子体振荡,试验及分析过程中忽略周向聚集振荡对壁面电势的影响。
2.2.3碰撞导致的振荡
霍尔推力器中存在形式多样的粒子碰撞,带电粒子之间的碰撞以及带电粒子与原子之间的碰撞都会产生振荡现象。对于非磁化等离子体中带电粒子的碰撞,其碰撞频率可表示为:
(6)
式中:T为粒子平均温度;ε0为真空介电常数;n为粒子密度;mα为碰撞粒子质量;Tα为碰撞粒子温度。
霍尔推力器工作过程中有离子-原子碰撞、电子-离子碰撞和电子-原子碰撞等碰撞模式。影响不同碰撞模式频率的因素主要有粒子的能量和粒子的质量。在粒子能量相近的情况下碰撞频率主要由粒子质量决定,从而不同粒子之间的碰撞频率最大相差约2~3个量级与图1给出的结果相符。由于外加电场和磁场的存在使得粒子运动变得较为复杂,通过理论分析很难给出推力器中实际振荡情况。实验测量方法往往可以更容易得到推力器碰撞产生的振荡与推力器工作参数的关系。
2.2.4低混杂波
低混杂波是一种垂直于磁场传播的静电离子波。对于静电波,波的传播方向与电场扰动的方向垂直,忽略磁场的变化。低混杂波的频率可以表示为:
(7)
式中:ωci为离子回旋频率;ωce为电子回旋频率;B为磁感应强度。
仅考虑原子的一次电离,霍尔推力器低混杂波频率与磁场强度成正比且与其它因素无关。对于霍尔推力器典型磁场参数(约200 Gs),相应低混杂波频率约为7 MHz。
3 电势振荡特性实验研究
由2.1节可知影响金属壁面电势的因素较多,根据霍尔推力器不同等离子体振荡模式频率分布范围及2.2节中分析,可以将实验中电势振荡频谱分为五种模式。通过分析这五种振荡模式随不同工作参数的变化情况,对霍尔推力器振荡与工作参数的关系进行研究。五种振荡模式分别为:F1(呼吸效应振荡,频率10~40 kHz)、F2(工质电离和激发振荡,频率40~100 kHz)、F3(电子-离子碰撞振荡,频率100~300 kHz)、F4(电子-原子碰撞振荡,频率0.6~1.5 kHz)和F5(低混杂波,频率1.5~8 MHz)。
3.1 不同放电电压电势振荡变化
放电电压变化会改变霍尔推力器中电势分布和等离子体的运动情况,从而对等离子体的振荡产生影响。研究放电电压与霍尔推力器各振荡模式的关系,有利于了解放电电压对霍尔推力器工作机制的影响,为霍尔推力器优化设计等提供参考。
图6所示为阳极流量20 sccm时,电势振荡频谱随放电电压的变化。随着放电电压的增加,推力器电势振荡高频部分的幅值有明显增加的趋势。由2.2节分析内容可知低频部分主要与原子的电离相关,而高频部分与电子的运动相关。高电压下电子运动速度的增加是导致高频部分振荡幅值增加的主要原因。
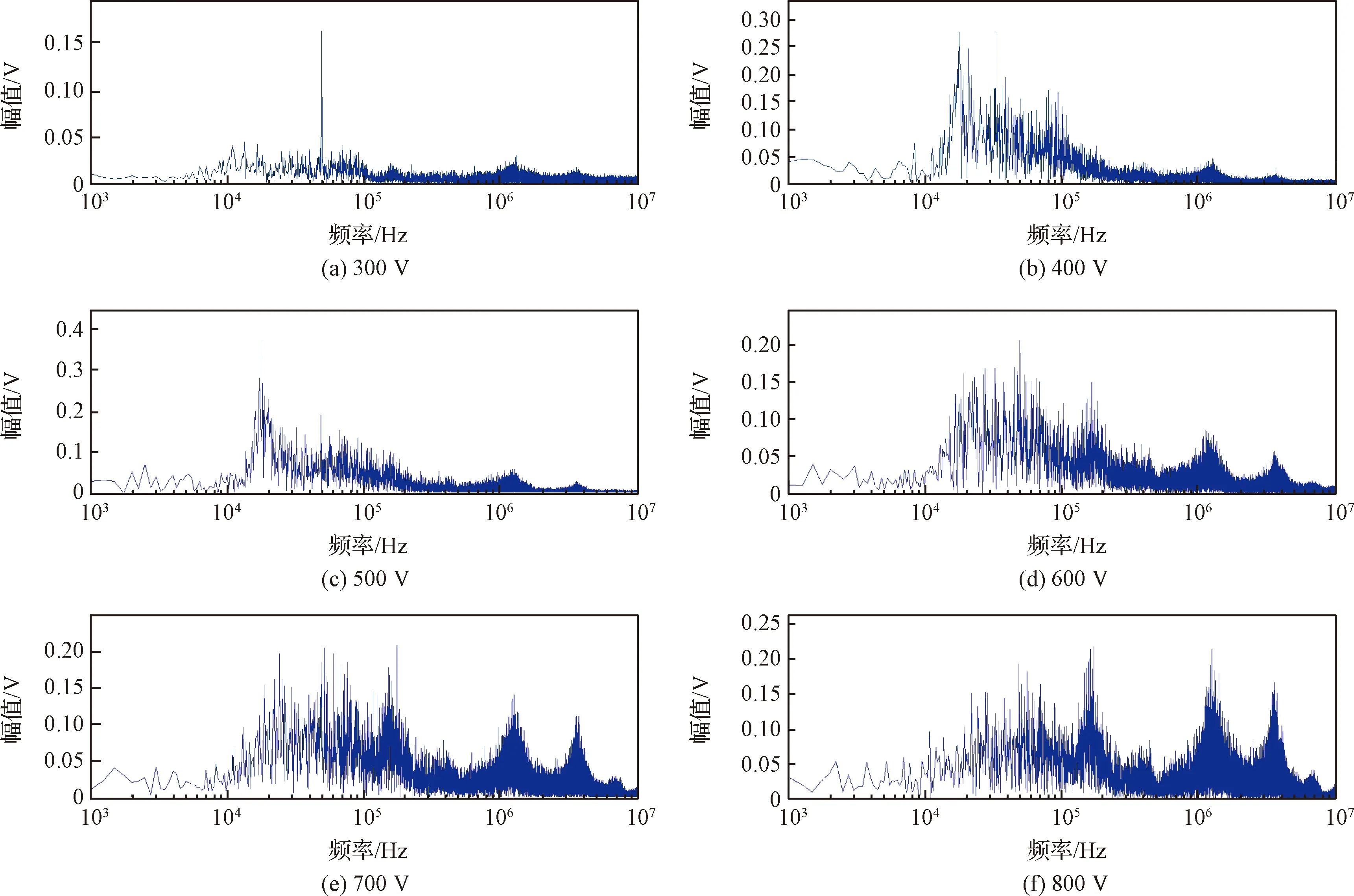
图6 不同放电电压下电势振荡频谱分布情况Fig.6 Spectrum distribution of potential oscillation under different discharge voltages
为了量化各振荡模式的相对强度,图7给出了不同流量下不同振荡模式最大振荡幅值随放电电压的变化情况。低流量情况下,F1在500 V时具有极大值,F2基本不随放电电压变化(即推力器中工质的电离和激发作用变化不明显)。大流量情况下,五种振荡模式基本都随放电电压逐渐增大。不同流量下,F3、F4和F5在大于500 V后均有明显的增大趋势,表明电压大于500 V时粒子之间的碰撞以及静电离子波都被明显加强。

图7 不同电势振荡模式的最大振荡幅值随电压变化情况Fig.7 Variation of the maximum oscillation amplitude of different potential oscillation modes with voltage
3.2 不同流量电势振荡变化
霍尔推力器阳极流量变化会导致放电室内工质密度发生变化,从而导致工质电离率和等离子体密度发生改变,进而使推力器内部的一些振荡模式发生变化。图8所示为200V工况下,不同流量电势振荡的频谱分布。阳极流量的变化对高频部分振荡幅值的影响较小,对低频部分有一定影响。根据2.2.1节分析,流量对低频振荡的影响主要是流量能够改变工质的密度,进而改变粒子运动速度和电离过程。

图8 不同流量下电势振荡频谱分布情况Fig.8 Potential oscillation spectrum distribution of different flow rates
图9所示为不同放电电压下,电势不同振荡模式最大振荡幅值随阳极流量的变化情况。200 V工况下,F1随阳极流量的增加而增大,高频段振荡的幅值基本不随阳极流量变化。400 V工况下,F1随阳极流量增加呈波动增加的趋势,高频段振荡幅值基本不发生变化。

图9 不同电势振荡模式最大振荡幅值随阳极流量变化Fig.9 Variation of the maximum oscillation amplitude of different potential oscillation modes with flow rates
3.3 不同磁场电势振荡变化
磁场构型和磁场强度均是影响霍尔推力器工作的重要因素,磁场对霍尔推力器内部等离子的振荡的影响是其中重要的研究方向之一[14-15]。由磁场仿真结果可知,内磁和外磁电流比约为0.9时,磁场处于对称位形。内磁电流增大,会导致内磁增强磁力线与放电室外壁面交点变多。外磁电流增大,会导致外磁增强,磁力线与放电室内壁面交点变多,进而导致低混杂波(平行与磁场的静电波)振荡幅值增加。
磁场位形的变化会导致带电粒子的运动方向以及粒子之间的相互作用发生变化,进而导致推力器工作时振荡发生变化。图10给出了不同振荡模式最大振荡幅值随磁路电流的变化云图。其中,F1在励磁电流较高或者较低(即磁场强度较高或者较低)时,具有较小的振荡幅值;励磁电流较小时,F2和F3最大幅值较大,F4最大幅值较小;F5在外磁较小的区域振荡幅值较小。此外,F1振荡幅值较大的模式对应的励磁电流呈带状分布(如图10(a)所示),在内磁较小时F1对应的振荡幅值相对较大。励磁电流较小或较大均能使呼吸效应的振荡幅值减小。当励磁电流较小时,磁场强度较弱,电子更容易穿越磁力线,导致电离区电子能量较高从而使工质的电离和激发的强度增加,电子与离子碰撞的最大能量升高(即振荡幅值增大),这时电子与原子弹性碰撞产生的振荡幅值相应减小(即F4幅值较小)。

图10 电势振荡最大幅值随励磁电流的变化Fig.10 The maximum amplitude of potential oscillation varies with excitation current
3.4 电势振荡与放电电流振荡对比
图11所示为阳极流量为20 sccm时,放电电流各振荡模式最大振荡幅值随放电电压的变化情况,与图7(a)所示对比可得:随着放电电压变化,放电电流振荡中F1的变化趋势基本与电势振荡一致。放电电流振荡中F2和F3在高电压部分随放电电压增加较慢。更高频率的F4和F5随放电电压没有明显的变化,很难通过放电电流的振荡研究相应振荡模式与放电电压的关系。改变其它工作参数时,放电电流振荡变化具有相似的规律。由此说明,金属壁面与阳极之间电势差的振荡可以得到比放电电流振荡更多的振荡信息。
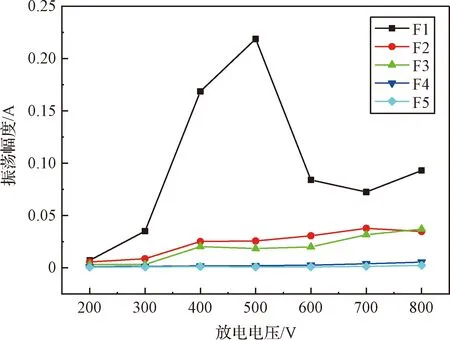
图11 放电电流不同振荡模式最大振荡幅值随放电电压的变化情况Fig.11 The variation of the discharge current in maximum oscillation amplitude with different oscillation modes with the discharge voltage
放电电流可以用以下公式表示:
Id=Iec+Iei+Iia
(8)
式中:Iec为由阴极产生并流入阳极的电子电流;Iei为电离过程产生并流入阳极的电子电流;Iia为到达阳极的离子电流。
将式(4)和式(8)进行对比可以得出:电势振荡比放电电流振荡包含更多振荡信息的原因主要来自两个方面:其一,电势振荡是测量放电室壁面与阳极之间的电势,放电室内部发生的等离子体振荡较多且能通过壁面电势的变化较好的反映出来。放电电流振荡则是测量阳极与阴极之间总的电子电流振荡,而放电室中的一些振荡很难直接反映在整个电路的电流中。其二,电势和电流对振荡的响应方式不同,使得不同振荡模式对应的电流和电势振荡幅值的相对大小发生变化。
4 结 论
本文根据金属-陶瓷复合放电室霍尔推力器的特点,对金属壁面与阳极之间电势差的振荡进行频谱分析,得出了不同工况下电势振荡频谱的分布情况,为霍尔推力器等离子体震荡研究提供了新思路。得出的结论如下:
1)理论分析和实验结果表明利用壁面电势研究霍尔推力器内等离子体振荡是可行的,并且通过电势可以获得比放电电流更多的振荡信息。
2)通过研究放电电压与电势振荡的关系发现,放电电压的增加会加大粒子间的碰撞以及低混杂波的幅值,但是呼吸效应在低流量下随放电电压的增加有先增加再减小的趋势。
3)在实验流量范围内,流量的增加会导致呼吸效应的强度发生变化,但是对除了呼吸效应外的碰撞振荡以及低混杂波影响较小。
4)对不同磁场情况下电势振荡的研究发现:呼吸效应振荡幅值较大的模式对应的励磁电流呈带状分布。外磁电流较大时,低混杂波幅值更大。磁场强度的增加会一定程度加剧电子和原子的碰撞、激发和电离。

