基于凸组合的麦克风阵列自适应语音增强方法研究

赵益波，陆浩志，李曙晖，严涛

1.南京信息工程大学电子与信息工程学院，江苏南京210044

2.江苏省大气环境与装备技术协同创新中心，江苏南京210044

麦克风阵列实质是一个声音采集系统，能够实时采集来自空间不同方向的信号。按照不同的应用场合，采取合适的几何排列，并加上对应的信号处理算法，可以有效解决诸如噪声抑制、去混响、声源定位等多种实际问题。将阵列信号处理技术引入到麦克风阵列中，所形成的麦克风阵列语音增强方法与单通道麦克风语音信号处理相比，在时域和频域的基础上增加了空域处理，可对来自空间不同方向的信号进行时-频-空域联合处理，弥补了单麦克风在噪声抑制、语音分离等方面的不足[1]。

自适应波束形成是麦克风阵列语音增强方法中最为流行使用的方法，广义旁瓣相消器（generalized sidelobe canceller，GSC）是一种基于最小均方差准则（minimum mean square error，MMSE）的自适应波束形成器[2]。GSC实现了自适应滤波与麦克风阵列技术的结合，将自适应波束的约束优化问题转化为无约束的优化问题[3]，在输入信号的先验知识极少甚至是未知的情况下，能够在最小均方差准则下通过误差信号不断地更新线性滤波器的权值，从而使输出噪声的功率最小化，以达到降噪的目的。最小均方差准则利用了误差信号的二阶统计量[4]，在理想的情况下，误差信号全部由高斯噪声组成，二阶统计量则包含了其全部的统计特征。利用二阶统计量通过最速下降法可以寻找到最优滤波系数以使均方误差达到最小，从而有效消除高斯噪声的影响，使得GSC对于高斯噪声环境下的目标信号,可以表现出良好的跟踪性能。但实际应用中除了高斯噪声外，还存在着大量的非高斯噪声，如α-稳定分布噪声、脉冲噪声等。二阶统计量一般不适用于非高斯环境，故使用传统的GSC对含脉冲噪声的语音信号进行降噪，效果会明显变差。诸多学者提出了多种去除非高斯噪声的方法，如文献[5]提出了一种相位匹配噪声估计的高阶谱去噪方法，通过高阶谱和相位匹配实时地逼近当前噪声，建立二次去除噪声方法，能有效去除高斯和非高斯噪声。文献[6]提出了一种中值滤波-小波阈值去噪算法，通过中值滤波抑制信号中的尖峰脉冲，并用小波阈值去除剩余噪声。文献[7]提出了一种新的自适应小波信号去噪法，在小波变换前将未知噪声信号转换为高斯噪声信号，再利用传统小波方法加以去噪，在非高斯噪声下能极大地提高信噪比。

凸组合滤波器中既有大步长的滤波器以加快收敛速度，又有小步长的滤波器以降低失调量[8]，对目标信号具有良好的追踪性能。基于此，本文提出一种基于凸组合的麦克风阵列自适应语音增强方法。该方法利用由线性滤波和非线性样条滤波构成的凸组合滤波器替换单一的线性自适应滤波器，并以最大相关熵准则自适应地更新凸组合滤波器的权值和非线性样条滤波中的控制点因子，有效滤除了混在目标信号中的高斯噪声和脉冲噪声，提高了输出信号的信噪比。

1 GSC语音增强原理

广义旁瓣相消器原理图如图1所示，分为上、下支路两部分。上支路仅包含固定波束形成器，下支路由阻塞矩阵和自适应滤波器两部分组成。麦克风阵列在接收来自不同方向角度的目标信号、干扰和噪声时，通常会存在一定的时延。分别通过时延估计和时延补偿两模块，对麦克风各阵元接收信号的延迟时间进行估计，并进行延迟校正，使得各路信号与所选参考阵元接收的信号达到同步状态。再选取合适的固定权系数，使同步信号经累加求和后可以在目标信号方向上形成一个主瓣波束，而在其他方向上形成波束零点，从而对干扰和噪声进行初步抑制。固定波束形成器的输出只存有目标信号和相干噪声，非相干噪声被滤除。

图1 广义旁瓣相消器原理框图Figure 1 Principle block diagram of generalized sidelobe canceller

下支路中阻塞矩阵的作用类似于带阻滤波器，它利用声源的空间方位信息进行构造，在期望信号的方向设置一个零陷点，滤除阵元接收信号中的期望信号，使阵元接收信号通过阻塞矩阵后仅输出噪声和干扰信号[9]。自适应滤波器以阻塞矩阵的输出作为输入信号，并以该输入信号作为上支路输出信号中残留噪声的参考信号，通过线性自适应滤波，输出估计噪声。将上、下支路的输出相减得到误差信号，再利用自适应算法不断地更新线性滤波器权值，最终使得自适应滤波器的输出无限接近于上支路的残留噪声或误差信号无限接近于零，从而有效滤除阵元接收信号中的干扰与噪声，获得纯净、清晰的目标信号。

2 基于凸组合的GSC语音增强方法

实际应用中的噪声繁多且复杂，除了高斯噪声外，大量的非高斯噪声充斥着真实环境，这些噪声表现为时域波形中突然出现的窄脉冲。在GSC中使用的线性滤波器对该类噪声的平滑效果较差[10]，研究表明非线性滤波却对此类噪声具有很强的鲁棒性。然而，当输入的语音信号中只存在高斯噪声，用单一的非线性滤波对其降噪，得到的处理效果又无法达到最优。鉴于此，本文提出利用凸组合滤波器代替线性自适应滤波器来协同去除目标信号中的高斯噪声和脉冲噪声。图2为提出的基于凸组合滤波器的麦克风阵列自适应语音增强方法的系统框图，该系统由固定波束形成器、阻塞矩阵和凸组合滤波器所构成，其中凸组合滤波器由线性自适应滤波和非线性样条自适应滤波构成。

图2分为上、下两个支路，假设入射信号为sn，其数量为P，麦克风阵元数为M，目标信号长度为N。xd(n)为第d个麦克风阵元所接收到的信号，有

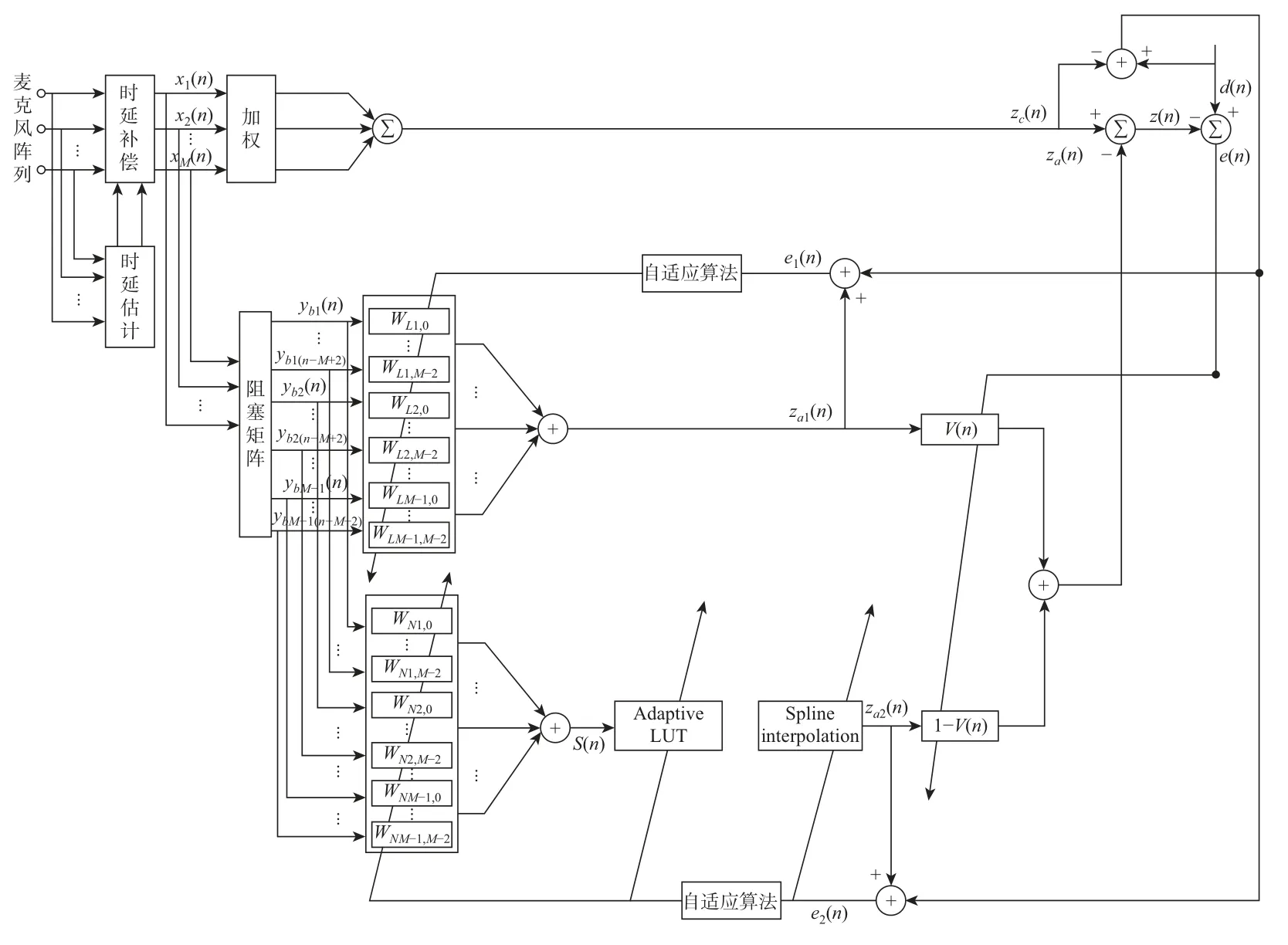
图2 基于凸组合的麦克风阵列自适应语音增强系统框图Figure 2 Block diagram of adaptive speech enhancement system for microphone array based on convex combination

式中：sn=[s1(n),s2(n),···,sp(n)]T，sp(n)是第p个入射信号，其长度为N，ad为第d个麦克风阵元接收信号的方向向量。那么根据式(1)可以推导出麦克风阵元接收到的信号xn为

式中：A=[a1,a2,a3,···,aM]T∈R M为阵列流型矩阵。该矩阵与各声源的入射角度与频率均有关。再经过累加求和后，上支路固定波束形成器的输出信号为

式中：xn=[x1(n),x2(n),···,xM(n)]T；Wc为设定的固定权系数向量，且Wc=C(CHC)−1c，C为约束矩阵，c为对应的约束响应向量。

为保证下支路的阻塞矩阵可以阻塞掉已同步信号中的目标信号，只需要使阻塞矩阵的每行元素之和为0。关于阻塞矩阵的构造有多种方法，如基于傅里叶正交基的构造方法、基于二项式对消的构造方法等[11]，这里选用由Griffiths和Jim提出的经典阻塞矩阵[12]

已同步信号xn经过阻塞矩阵B后的输出信号为

设B的第m行行向量为，则对于所有的m来说需满足

式中，bm之间是线性独立的，故阻塞矩阵B的输出yb,n最多由M−1个线性独立的元素组成[13]，也就是说yb,n为M−1路噪声与干扰信号。记ybg(n)为阻塞矩阵输出的第g路噪声信号。

阻塞矩阵之后接入一个凸组合滤波器，该凸组合滤波器由具有抽头延迟结构的线性自适应滤波器和非线性样条自适应滤波器组成。线性自适应滤波器中所应用的自适应滤波算法一般为最小均方算法（least mean square，LMS）。当然，像递归最小二乘算法（recursive least squares，RLS）等也是常用的噪声抑制算法，且RLS滤波器可以在非平稳环境中表现出优越的追踪性能[14]，但因算法计算复杂度较高，一般情况下在GSC中并不优先选用。

当M−1路噪声信号经过凸组合滤波器中的线性滤波器后，输出信号za1(n)为

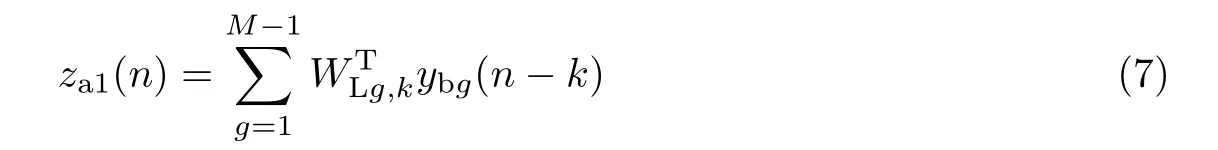
式中：WLg,k=[WLg,0,WLg,1,···,WLg,M−2]T，g=(1,2,3,···,M−1)，k=(0,1,2,···,M−2)是线性滤波器的滤波系数；ybg(n−k)=[ybg(n),ybg(n−1),ybg(n−2),···,ybg(n−M+2)]T是第g路噪声信号的M−1个延迟。用纯净的目标信号d(n)减去上支路固定波束形成器的输出zc(n)，再加上线性滤波器的输出za1(n)，便可得到误差信号e1(n)为

非线性滤波中最常用的是模块化表示，如Wiener模型和Hammerstein模型以及由这两种模型串、并连接所产生的系统架构等[15]。Wiener模型非线性系统由线性时不变（linear time invariant，LTI）滤波器和一个静态非线性函数两部分组成，且线性时不变滤波器置于非线性函数前面。Hammerstein模型非线性系统组成部分和Wiener型类似，区别是非线性函数置于线性滤波器前面。系统采用Wiener模型非线性结构，由线性滤波器、自适应查表（look-up table，LUT）和局部低阶多项式样条曲线插值构成非线性滤波器。

在Wiener模型非线性结构中，阻塞矩阵输出的M−1路噪声先进入线性滤波器中，其输出为

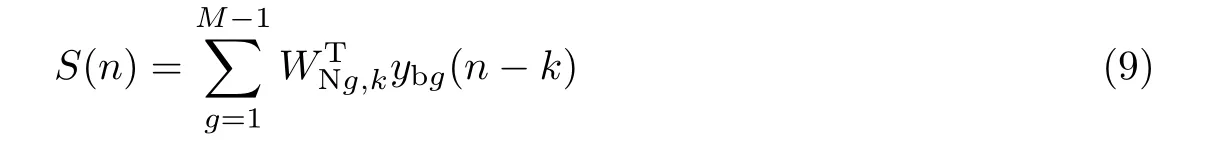
式中：WNg,k=[WNg,0,WNg,1,···,WNg,M−2]T,g=(1,2,3,···,M−1),k=(0,1,2,···,M−2)为非线性滤波中线性自适应滤波器的滤波系数。且输出的信号S(n)进一步作为非线性函数的输入。

在非线性函数中，包括两个参数：局部参数u和跨度指数i，它们均是线性滤波器的输出S(n)的函数，两参数的定义式分别如下：

式中：[·]为取整运算；Δx为插值点的间隔；Q为控制点的数量。样条曲线定义为通过在自适应查表中对定义的控制点进行插值的光滑参数曲线，B样条和C-R样条是两个最常用的三次样条曲线[16]。因为C-R样条曲线在局部逼近方面有着更好的性能，所以本文采用该样条曲线，其基矩阵为

非线性样条滤波器的输出za2(n)是关于u函数，其定义为

式中：u=[u3,u2,u,1]T；qi,n=[qi,qi+1,qi+2,qi+3]T。则非线性样条滤波的误差信号为

将线性滤波器的输出和非线性样条滤波器的输出进行合并，则整个凸组合滤波器的输出za(n)为

式中：V(n)为凸组合滤波器的混合系数，取值为

式中：a(n)用来调节混合系数V(n)。将纯净目标信号d(n)和上支路固定波束形成器的输出zc(n)相减，再加上凸组合滤波器的输出za(n)，得到总误差信号e(n)为

在更新线性滤波器的系数和非线性样条滤波的控制点时，采用最大相关熵准则[17]（maximum correntropy criterion，MCC）取代传统GSC中使用的最小均方差准则。相关熵描述的是两个随机变量之间的非线性相似度量，当其被应用于自适应滤波时，可以将最大相关熵准则理解为最大化期望信号与滤波器输出信号之间的相关熵。该准则考虑了信号的高阶统计量特征，可以更加准确地评估出输入输出信号的误差[18]，使对滤波系数的搜索调整为最优方向。此外，在该准则下，一旦误差出现异常值，滤波系数更新的叠加量几乎为零，所以在非线性系统和脉冲噪声中可以表现出强鲁棒性，对脉冲噪声去除能力强。

线性滤波器系数自适应更新式为

式中：µL为步长因子；σ为高斯核宽度。核宽度一般取值为常数，它是影响核函数性能的重要因素，控制着两个随机变量相似程度的范围，通过调节核宽度的取值，能够改变最大相关熵控制的相似度度量的局部程度[19]。当LMS算法的优化准则被替换为最大相关熵准则时，高斯核函数可以根据核宽度取值的不同而调整对期望信号与滤波器输出信号间相关熵的局部控制能力，且其对非线性信号有着优越的处理性能，则选用核函数时一般考虑选用高斯核函数。

非线性样条滤波中的滤波器系数和控制点自适应更新式分别为

式中：µN为非线性滤波中的线性滤波器系数更新的步长因子，其取值要比µL值要小，这样既可以加快整个自适应滤波的收敛过程，又能获得较小的稳态失调。为ψi(u)的导数；µq为控制点自适应调整的步长因子。凸组合滤波器的混合系数更新式分别为

式中：µ为步长因子；r(n)用来调节a(n)，其更新式为

式中：β是调节因子，为定值。最终处理后的输出为

3 仿真实验

仿真实验在Matlab R2017a软件中进行。为验证所提出的语音增强方法比传统的广义旁瓣相消算法的降噪效果更优越，在施加相同的条件下对比两种方法的降噪效果。仿真实验共进行了两组，两组实验施加的相同条件为：纯净的目标语音信号为“酷狗”音乐软件打开时的提示音，其内容为“Hello，酷狗”，采样频率为8.0 kHz，来波方向为10°加入的具有方向性的干扰噪声为Windows XP系统的经典开机音乐，采样频率为44.1 kHz，来波方向为60°同时为麦克风阵元的接收信号加入高斯白噪声和显著的固定脉冲噪声，并分别以加入信噪比为20 dB和30 dB的高斯白噪声作为两组实验的唯一不同条件。脉冲噪声采用由标准参数系下生成的α-稳定分布噪声所形成的音频文件，其中α取值为1.3，ζ取值为0，γ取值为0.01，λ取值为0，参数α、ζ、γ、λ分别为特征指数、对称参数、分散系数和位置参数[20]。另外，高斯核宽度σ取值为0.1。

将加入信噪比为20 dB的高斯白噪声作为第一组实验，实验仿真结果如图3～8所示。图3为纯净目标语音信号，图4和5分别为方向性干扰和脉冲噪声。图6为加入了20 dB高斯噪声和固定脉冲噪声的麦克风阵元接收信号，图7和8分别为传统广义旁瓣相消算法和本文所提方法处理后得到的语音增强信号。

图3 纯净语音信号Figure 3 Pure speech signal

图4 方向性干扰信号Figure 4 Directional interference signal

图6 加入了20 dB的高斯白噪声和脉冲噪声的麦克风阵元接收信号Figure 6 Microphone array element receiving signal with 20 dB Gaussian white noise and impulse noise added

从图7中可以看出，经传统GSC处理后所得的语音增强信号中“毛刺”较多，说明依旧残留着较多的脉冲噪声，且相较于纯净目标语音信号，波形出现失真。而从图8可以看出，经本文所提方法处理后所得的语音增强信号中只残留着极少量的脉冲噪声，且波形较之于纯净目标语音信号的波形，只存在微弱的差异，说明本文方法相比于传统GSC的降噪效果更优越，更有效。

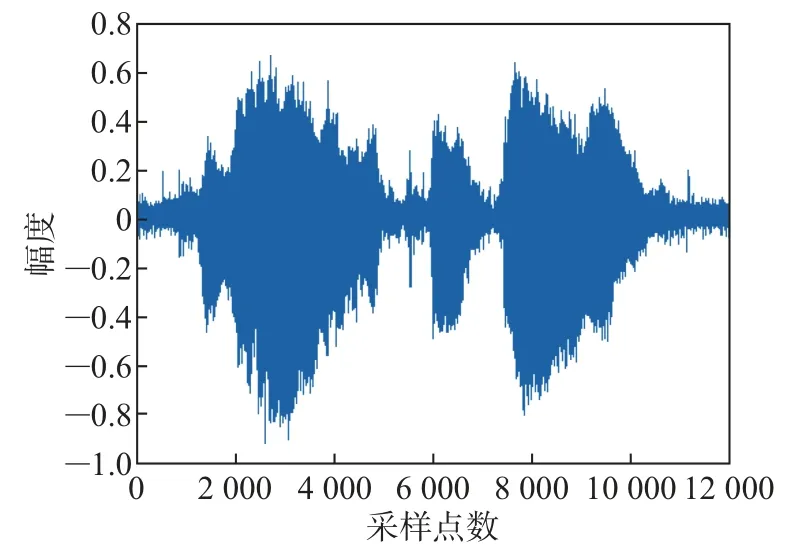
图8 本文所提方法处理后的语音信号Figure 8 Speech signal processed by the method proposed in this paper

将加入信噪比为30 dB的高斯白噪声作为第二组实验，得到的仿真实验结果如图9～11所示。图9为加入了30 dB的高斯噪声和固定脉冲噪声的麦克风阵元接收信号，图10为传统广义旁瓣相消算法处理后的语音增强信号。图11为本文所提方法处理后的语音增强信号。

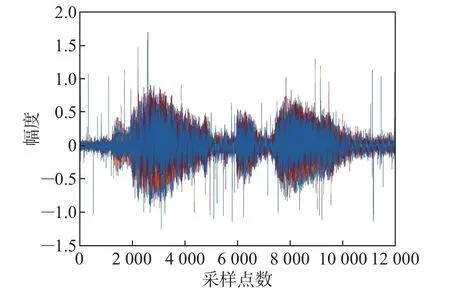
图9 加入了30 dB的高斯白噪声和脉冲噪声的麦克风阵元接收信号Figure 9 Microphone array element receiving signal with 30 dB Gaussian white noise and impulse noise added

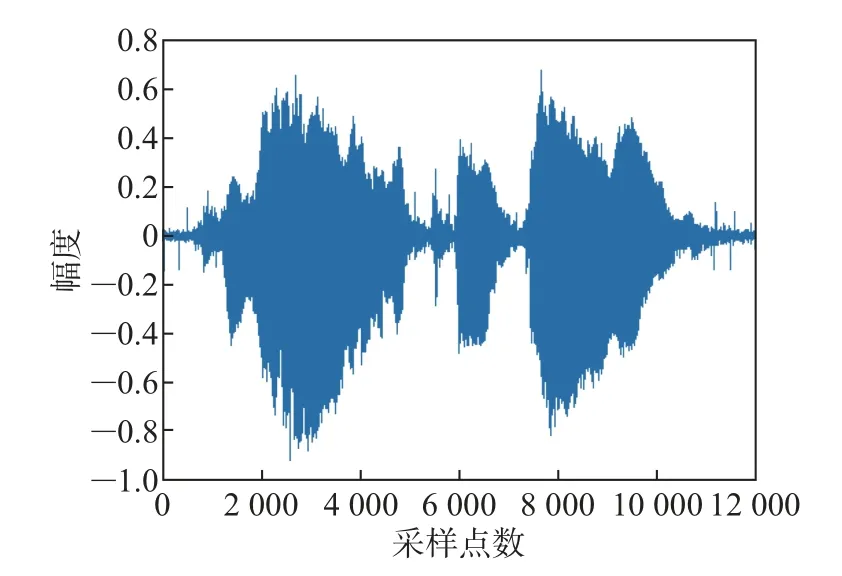
图11 本文所提方法处理后的语音信号Figure 11 Speech signal processed by the method proposed in this paper

比较图10和11可以明显看出，经本文所提方法处理后的语音增强信号中基本不存在脉冲噪声，而经传统方法处理后的语音信号还存在着少量的脉冲噪声。综合比较图7～8、图10～11这4幅图，可以得出本文所提语音增强方法比传统GSC对高斯噪声和脉冲噪声的抑制效果更好，鲁棒性更强，对纯净语音信号有明显的增强效果。

图5 脉冲噪声Figure 5 Impulse noise

图7 传统GSC处理后的语音信号Figure 7 Speech signal processed by traditional GSC

图10 传统GSC处理后的语音信号Figure 10 Speech signal processed by traditional GSC

进一步，采用信噪比（signal-to-noise ratio，SNR）、分段信噪比（segment signal-to-noise ratio，SegSNR）两种评价指标分别对传统GSC和所提方法处理后的语音信号质量进行评价。

信噪比是衡量针对宽带噪声失真的语音增强算法的常规方法，主要计算整个时间轴上语音信号与噪声的平均功率之比，表1给出了两种方法处理后的增强语音信号的信噪比值。

表1 经两种方法处理后的信噪比值Table 1 SNR processed by two methods dB

由表1可知，当加入信噪比为20 dB的高斯白噪声时，经传统GSC处理后所得增强语音的信噪比为8.37 dB，而采用所提方法却达到了15.76 dB，相比于传统GSC，信噪比提高了7.39 dB。当高斯白噪声的信噪比为30 dB时，传统GSC输出信噪比为9.53 dB，而本文方法相比于传统GSC的输出信噪比提高了9.57 dB。

语音信号是一种短时平稳信号，在不同帧内的信噪比是不相同的，因此采用分段信噪比进一步对两种方法的处理结果进行评价更具有说服力。表2分别给出了两种方法处理后语音增强信号的分段信噪比值。

表2 经两种方法处理后的分段信噪比值Table 2 SegSNR processed by two methods dB

由表2可以看出，不论加入的高斯白噪声的信噪比为20 dB还是30 dB，所提方法处理后语音增强信号的分段信噪比均比传统GSC输出的分段信噪比要高，分别提高了4.31 dB和5.97 dB。仿真实验波形与表1和2数据显示，所提出的语音增强方法比传统GSC的降噪效果更明显，对高斯噪声与脉冲噪声均表现出了很强的鲁棒性。

4 结语

本文提出了一种基于凸组合滤波器的麦克风阵列自适应语音增强方法，利用线性滤波和非线性样条滤波组成的凸组合滤波器取代了传统GSC中的线性滤波器，并以最大相关熵准则更改了自适应滤波算法中的代价函数和优化准则，使得该方法对脉冲噪声表现出强鲁棒性。仿真实验结果表明，所提方法较传统GSC去高斯和脉冲噪声效果更明显，鲁棒性更强。