基于Park—WPT和WOA—LSSVM的异步电动机故障诊断方法
恵阿丽, 鹿伟强, 荣相, 魏礼鹏, 陈雯雅
(1.西安科技大学 电气与控制工程学院, 陕西 西安 710054;2.中煤科工集团常州研究院有限公司, 江苏 常州 213015;3.天地(常州)自动化股份有限公司, 江苏 常州 213015)
0 引言
异步电动机具有结构简单、效率高、鲁棒性强等优点,在电力、煤炭、交通运输和航空航天等领域中都有广泛应用。在各种电气传动系统中,有90%左右采用感应电动机驱动;在电网总负载中,异步电动机占60%左右[1]。但严酷的工作环境及制造缺陷等问题,使得异步电动机的转子和轴承易发生各类故障。转子刚度不足、轴承磨损和安装误差等会导致转子断条和气隙偏心故障[2]。转子断条故障是最常见的故障类型,主要由转子端环和导条开焊、断裂造成[3],若未及时检测到故障,会导致故障进一步扩大,出现多根转子断裂。气隙偏心故障轻则使气隙磁场产生畸变,恶化电动机各项性能指标;重则会使定转子相擦,电动机烧毁。因此,对异步电动机的转子断条、气隙偏心及其混合故障进行识别诊断显得尤为重要。
目前针对三相异步电动机的单一故障诊断方法已经有了大量研究并取得了显著效果。文献[4]使用旋转不变信号参数估计方法对三相定子电流信号的Park矢量模平方函数进行处理,避免了噪声和负荷波动的影响,对转子断条故障特征进行了准确识别。文献[5]基于集合经验模态分解技术提取有效的Hilbert时频谱能量特征,对电动机的气隙偏心故障进行了准确诊断。文献[6]使用Park矢量变换求取dq两相中的电流坐标,以q轴为参考轴,提取d轴上的最大值和最小值作为特征向量,对异步电动机匝间短路故障进行了识别。然而,这些方法仅完成了异步电动机内部某一类型故障的诊断。由于异步电动机故障原因复杂,故障特征之间具有较强的非线性关系,所以对电动机多故障特征提取和诊断是当前研究的重点。
电动机多故障诊断技术主要包括2种:一是同类信号多特征提取技术[7-8],二是异类信号特征融合提取技术[9-10]。文献[7]提出了基于三相定子电流信号的多种Park矢量变换法,通过对不同电动机故障特征添加幅值和相位校正因子,有效识别出定转子故障和轴承故障。文献[8]使用短时傅里叶变换提取各故障频谱图,通过卷积神经网络有效识别出转子故障和轴承故障。但同类信号多特征提取技术存在诊断精度较差的问题,随着传感器技术的发展,研究人员提出了基于异类信号的电动机故障提取方法。文献[9-10]基于电动机振动信号和电流信号,对电动机转子和轴承故障进行了有效诊断。异类信号的引入使得故障特征提取更加有效,但是也增加了故障检测的成本,此外各类传感器的安装位置和采集信号的利用率问题也随之而来[11]。
综合考虑2种技术的优缺点,本文采用同类信号多特征提取技术,基于三相定子电流信号对异步电动机转子断条、气隙偏心及其混合故障进行研究,提出了基于Park-WPT(Park-Wavelet Packet Transform,Park矢量变换融合小波包变换)和WOA-LSSVM(Whale Optimization Algorithm-Least Squares Support Vector Machine,鲸鱼优化的最小二乘支持向量机)的三相异步电动机故障诊断方法。通过Park矢量变换对采集到的三相电流信号进行预处理,根据椭圆轨迹的畸变率提取其第1类特征量;根据扩展Park矢量法求出dq两相的模平方值,并得到其一维波形,使用WPT对信号进行分解,求取系数能量作为第2类特征量;依据提取的2类特征信号建立WOA-LSSVM故障诊断模型。实验结果表明,该方法相比于单一特征提取方法具有更高的准确度,实现了同类信号特征的精确提取,能够较好地实现异步电动机转子多故障诊断。
1 故障特征提取
1.1 基于Park矢量变换的故障特征提取
Park矢量变换也称ABC/dq变换,基本原理是将三相坐标系下的定子电流(iA,iB,iC)转换为两相坐标轴下的定子电流(id,iq)。
将三相静止坐标系ABC投影到两相静止坐标系αβ中,即进行Clark变换。
(1)
式中iα,iβ为两相静止坐标系αβ中的电流。
通过Park矢量变换将两相静止坐标系αβ等效到两相旋转坐标系dq上。
(2)
式中θ为d轴与α轴的夹角。
根据式(2)可得id,iq的模值R:
(3)
由式(3)可知,id,iq形成的矢量轨迹是一个以原点为中心的圆。实际上,由于制造、安装和材料等原因,正常异步电动机的矢量轨迹只能接近圆。当异步电动机出现各种故障时,电流信号的相应关系发生变化,导致矢量偏离圆轨迹,变成椭圆,因此,椭圆长短轴的长度变化与电动机故障类型和程度有一定联系[12]。健康电动机、转子断条故障、气隙偏心故障和混合故障状态下的定子电流Park矢量模轨迹如图1所示。
由图1可知,不同故障条件下的轨迹图形具有明显差异,分别求取内外圈畸变率Grate作为提取的特征量。
(4)


图1 定子电流Park矢量模轨迹Fig.1 Trajectories of stator current Park vector modulo
式中Rmin,Rmax分别为R的最小值和最大值。
1.2 基于小波包能量的故障特征提取
为了更加精确地提取故障特征,考虑负载变化、三相输入电压不平衡对畸变率的影响,引入扩展Park矢量法。通过求取矢量模平方IEPVA,将三相定子电信号转换为一维时间序列信号,再对IEPVA进行频谱分析,以提高特征提取精度。
IEPVA=|id+jiq|2
(5)
电动机4种状态下的定子电流Park矢量模平方波形如图2所示,其中t为时间。
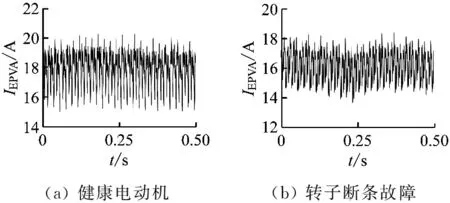

图2 定子电流Park矢量模平方波形Fig.2 Waveforms of square of stator current Park vector modulo
WPT是目前故障特征提取技术中较为常用的方法,其思想是利用小波包分解将不同类型的故障信号在频域上分解为若干个频段,根据不同故障信号在各频段的能量不同进行特征提取[13]。3层小波包分解如图3所示。其中S(0,0)为原始信号,S(p,v)(p=0,1,2,3;v=0,1,…,7)为分解树第p层的第v个节点。
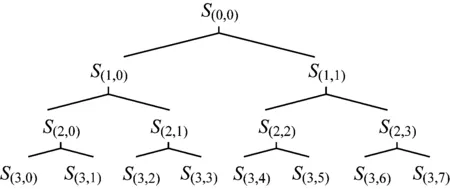
图3 3层小波包分解Fig.3 3-layer wavelet packet decomposition
利用小波包对故障原始信号进行特征提取的步骤如下:
(1) 对Park矢量模平方谱进行第p层小波包分解,提取信号特征,小波包分解的递推公式为
(6)
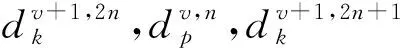
(2) 求各频带信号的能量,令Ep,v为第p层第v个节点S(p,v)的能量,则
(7)
式中dv,k为S(p,v)的小波包系数。
(3) 利用所求能量构造故障特征向量E,并将其作为故障诊断算法的输入量,即
E=[Ep,0,Ep,1,…,Ep,2p-1]
(8)
2 WOA-LSSVM算法
2.1 LSSVM
LSSVM是标准SVM(Support Vector Machine)的改进,将传统SVM中不等式约束改为等式约束,使求解最优化问题变为求解线性方程,从而提高算法的运算速度和收敛精度。
LSSVM算法采用函数f(x)对样本数据建模:
f(x)=ωTφ(x)+b+ξj
(9)
式中:x为训练样本的输入向量;ω为超平面的权重向量;φ(x)为非线性映射函数;b为偏置常数;ξj为拟合误差,是第j组数据实际训练输出与估计输出的误差量。
ω和b可由以下优化问题求得:
(10)
式中:J为正规化函数;λ为正则化参数,λ>0;N为样本点数量。
空间向量第j个维度下的约束方程为
yj=ωTφ(xj)+b+ξj
(11)
式中xj为第j个维度下的输入信号。
式(10)的最优解可通过对偶形式得出。根据对偶形式建立拉格朗日函数,即
(12)
式中γj为拉格朗日乘子系数。
依据KKT(Karush-Kuhn-Tucker)最优化条件,令式(12)对ω,b,ξj,γj求偏导的值为0,得到最优化条件:
(13)
消去ω,ξj,并采用核函数方法做进一步处理,令核函数H(x,xj)=φT(x)φ(xj),满足Mercer条件,则LSSVM回归函数为
(14)
核函数H(x,xj)的形式有多种,常用的有sigmoid感知核函数、多项式核函数和径向基核函数等。由于电动机故障类型与所提取特征向量之间具有非线性关系[14],故本文选取适用于解决非线性问题的径向基核函数:
(15)
式中σ为径向基核函数的核宽度。
正则化参数λ和核宽度σ对LSSVM分类模型具有较大影响,因此,对于正则化参数λ和核宽度σ的优化尤为关键。
2.2 WOA-LSSVM算法流程
WOA是通过模拟座头鲸收缩包围猎物、螺旋更新猎物位置的机制来实现优化搜索的全局算法[15],具有调整参数少、收敛速度快、可避免陷入局部最优的优点。
(1) 收缩包围机制。座头鲸识别猎物的位置并将其包围,WOA假定当前的最佳候选解是目标猎物或接近最优解,如果存在更优解则在每次迭代中更新位置,这一行为可表示为
D=|QX*(m)-X(m)|
(16)
X(m+1)=X*(m)-PD
(17)
P=2ɑr1-ɑ
(18)
Q=2r2
(19)

(20)
式中:D为鲸鱼的最优位置与当前位置的绝对差值;Q,A为系数向量;X*(m)为当前鲸鱼的最优位置;m为当前迭代次数;X(m)为当前鲸鱼位置;ɑ为控制参数,随着迭代次数增加,ɑ从2线性减小到0;r1和r2为[0,1]的随机向量;Mmax为最大迭代数。
(2) 螺旋更新位置。座头鲸包围猎物后,以螺旋状运动方式捕获猎物,其数学模型为
X(m+1)=X*(m)+Dexp(b′m)cos(2πl)
(21)
式中:b′为常数,用来定义对数螺线的形状;l为[-1,1]的随机数。
鲸鱼的收缩包围机制和螺旋更新位置是一种同步行为,假设2种模式各有50%的可能性,则鲸鱼的位置更新方程为
X(m+1)=
(22)
式中u为[0,1]的随机数,根据u的值,WOA可在螺旋运动和圆周运动之间切换。
WOA-LSSVM算法流程如图4所示。首先,初始化WOA和LSSVM参数;其次,计算鲸鱼种群个体的适应度,根据最优适应度值确定当前最优个体,并通过算法迭代更新鲸鱼个体位置,得到最优个体结果;然后,根据最优结果确定LSSVM中的正则化参数λ和核宽度σ;最后,对测试集进行诊断分类。

图4 WOA-LSSVM算法流程Fig.4 Flow of WOA-LSSVM algorithm
3 异步电动机故障诊断流程
基于Park-WPT技术对异步电动机故障特征进行提取与识别,结合WOA-LSSVM实现电动机转子系统多故障诊断。诊断流程如图5所示,主要包括数据采集、特征提取和故障诊断3个方面。使用电流传感器和采集卡实现数据采集;采用Park-WPT技术实现2类特征的提取,并通过归一化处理[13]将结果值映射到0~1;根据WOA优化的LSSVM建立故障诊断模型,实现多故障诊断。
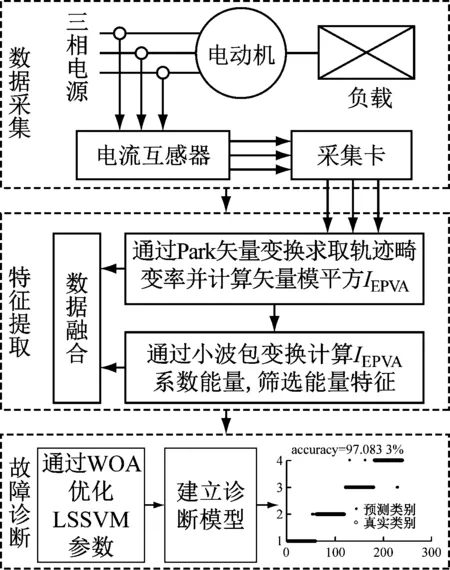
图5 电动机故障诊断流程Fig.5 Flow of motor fault diagnosis
4 实验分析
为获得异步电动机转子系统多故障实际数据,在实验室环境下搭建电动机故障实验平台,对基于Park-WPT和WOA-LSSVM的转子多故障诊断方法进行了完整的实验验证、数据处理和结果分析。
4.1 实验设计
实验所用电动机为4极YE3-100L2型异步电动机,额定电压为380 V,额定功率为3 kW,额定转速为1 420 r/min。为了真实模拟断条故障,在转子制作过程中人为将导条钻孔断开(孔径为0.8 cm),如图6(a)所示。将电动机轴承端盖的内圈扩大5 mm,并通过4个螺栓控制轴承端盖的位置,如图6(b)所示。当轴承端盖的位置不变时,模拟静态偏心故障;当轴承端盖的位置改变时,模拟动态偏心故障。另外,为确保不会引入新的故障类型,对电动机进行了动平衡实验,排除了后续实验中转子偏心故障对断条故障检测可能造成的干扰。

(a) 转子断条故障

(b) 气隙偏心故障图6 转子断条、气隙偏心故障Fig.6 The faults of rotor broken bar and air gap eccentricity
实验中共使用6台同型号电动机,包括健康电动机2台、转子单根导条断裂电动机( 断裂位置为导条中央) 1台、转子2根导条断裂电动机( 断裂位置为相邻2根导条的中央) 1台、动态偏心故障和静态偏心故障电动机1台、混合故障电动机1台。实验所用采集设备为3个霍尔电流传感器。电动机故障检测实验平台如图7所示。

图7 电动机故障检测实验平台Fig.7 Motor fault detection experiment platform
4.2 故障特征提取
分别采集空载、20%负载、60%负载和额定负载情况下各台电动机三相线电流波形,采样频率为10 kHz。根据式(4)分别提取内圈畸变和外圈畸变特征,得到异步电动机不同负载下的畸变特征波形,如图8和图9所示。

图8 不同负载下内畸变特征趋势Fig.8 Trends of internal distortion characteristics under different loads
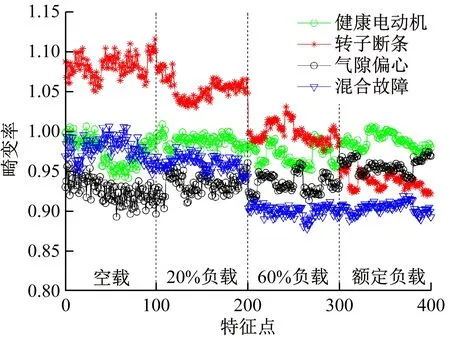
图9 不同负载下外畸变特征趋势Fig.9 Trends of external distortion characteristics under different loads
由图8和图9可知,在各负载情况下,根据畸变率可以有效识别健康电动机、转子断条故障和气隙偏心故障。健康电动机的畸变率在0.94~1.02波动,与理论值1比较接近;转子断条故障的畸变率随负载的增加有明显的下降趋势;气隙偏心故障随着负载的增加呈现上升趋势;混合故障的特征在60%以上负载时与其他故障具有明显差别,而在60%以下负载时与健康电动机和气隙偏心故障有大量的重合区域,识别效果较差。此外,受电源波动和电动机环境的影响,畸变率会出现少量突变值,因此,依据单一的畸变率特征不能准确分辨出各类型电动机故障。
对IEPVA波形进行5层小波分解,基函数选取常见的db3小波,设置能量占比阈值为0.1,即考虑能量占比较大的频段。额定负载下电动机各节点频段能量占比如图10所示。由图10可知,各频段的小波能量占比具有微弱差异,但总体趋势基本相似,通过能量占比阈值可以筛选出频段1,2,4。

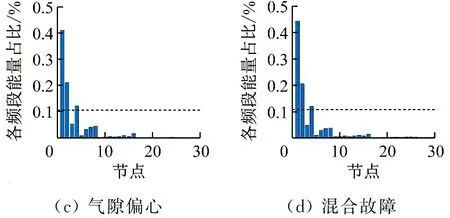
图10 额定负载下电动机各频段能量占比Fig.10 The proportion of energy in each frequency band of the motor under rated load
根据电动机能量占比可得不同状态下的特征提取点,如图11所示,其中能量占比1、能量占比2、能量占比3分别为频段1,2,4的能量占比。根据3个频段的能量占比特征可以清晰地分辨电动机是否为故障状态,但在特征点的边缘会出现重叠,尤其是混合故障特征点会同时与断条故障和偏心故障特征点重合,这是故障特征提取的难点所在,在电动机实际应用中是不可避免的问题。

图11 不同状态下电动机特征提取点Fig.11 Characteristic extraction points of motors in different states
针对上述2类特征提取方法的不足,将内外畸变率特征和3个较大能量占比特征进行组合,构成一组5维多特征向量,输入故障诊断算法中进行识别。
4.3 故障识别与诊断
对提取的800组特征信号进行标记,其中健康电动机标记为1,断条故障电动机标记为2,偏心故障电动机标记为3,混合故障电动机标记为4。选取560组数据作为训练集,240组数据作为测试集,将迭代寻优后的最优参数代入到LSSVM中进行故障识别与诊断,结果如图12所示。

图12 Park-WPT+WOA-LSSVM诊断结果Fig.12 Park-WPT+WOA-LSSVM diagnosis results
为了验证Park-WPT特征融合方法的有效性,与单一特征提取方法的诊断结果进行对比分析。图13和图14分别给出了Park+WOA-LSSVM和WPT+WOA-LSSVM的故障诊断结果。

图13 Park+WOA-LSSVM诊断结果Fig.13 Park+WOA-LSSVM diagnosis results

图14 WPT+WOA-LSSVM诊断结果Fig.14 WPT+WOA-LSSVM diagnosis results
对比可知,Park-WPT+WOA-LSSVM方法的故障识别率可达97.08%,而Park+WOA-LSSVM,WPT+WOA-LSSVM方法的故障特征识别率分别为73.75%和88.33%,证明本文所提方法可有效提高故障识别率。
4.4 诊断算法对比
为了验证Park-WPT+ WOA-LSSVM 方法的性能,将Park-WPT提取的多特征量分别输入PSO(粒子群优化)算法、GWO(灰狼优化)算法和GA(遗传算法)优化的LSSVM中进行对比实验,算法最大迭代次数均为50,测试结果见表1。由表1可看出,WOA和GWO算法的寻优速度都较快,WOA算法的正确率更高,说明WOA的性能更优。

表1 电动机多故障诊断算法对比Table 1 Comparison of multiple fault diagnosis algorithms for motors
5 结论
(1) 基于Park矢量变换的故障特征提取和基于小波包能量的故障特征提取方法可以识别出电动机是否为故障状态,但在特征点的边缘会出现重叠,尤其是混合故障特征点会与其他状态特征点重合,对混合故障的识别效果较差。对2种方法进行融合,将内外畸变率特征和3个较大能量占比特征组合成一组5维多特征向量,再通过诊断算法进行识别,可有效提高故障识别率。
(2) 采用WOA的收缩包围猎物和螺旋更新猎物位置的机制优化LSSVM中的正则化参数和核宽度,根据提取的2类特征信号建立以WOA-LSSVM为基础的故障诊断模型。
(3) 实验结果表明,基于Park矢量变换或小波包变换的单一特征提取算法对混合故障的识别效果较差,故障特征识别率分别为73.75%和88.33%,将2类特征组合后,故障识别率提高到97.08%;WOA-LSSVM的寻优速度较快,故障诊断正确率较高,综合性能优于PSO算法、GWO算法和GA优化的LSSVM。

