矿井带式输送机多电动机同步控制技术
程国栋, 吴玮
(1.中国矿业大学 徐海学院, 江苏 徐州 221008;2.江苏建筑职业技术学院 建筑智能学院, 江苏 徐州 221008)
0 引言
矿井长距离带式输送机一般采用多点驱动方式,以防止张力不均匀或过大造成输送带损伤。常见的有在中部或尾部增加驱动点,各驱动点之间距离较远,为保证多电动机传动系统安全运行和生产效率,须对驱动电动机进行转速同步控制[1-4]。
目前多电动机同步控制策略主要有并行控制[5]、主从控制[6]、交叉耦合控制[7]、相邻耦合控制[8]和偏差耦合控制。其中,偏差耦合控制具有耦合度高、同步性能好、适用电动机类型多等优点,已被广泛应用于各类多电动机传动场合。文献[9]首次提出了偏差耦合控制的思想,利用电动机之间的转速差构造转速同步补偿器,在3台电动机平台上验证了其具有较好的同步精度和动态抗扰性能。文献[10]提出了一种基于单神经元PID的变增益速度补偿器进行偏差耦合控制,比PID固定增益速度补偿器具有更好的收敛性及鲁棒性。文献[11]利用快速非奇异终端滑模控制算法对偏差耦合控制进行了改进。文献[12]利用线性系统校正原理实现了多电动机传动系统的同步性能与跟踪性能的解耦控制,同时设计了转速环的输出选择函数,具有良好的同步性能。文献[13]提出了虚拟电动机的概念,使得所有电动机均跟踪虚拟电动机的运行轨迹,以减小各电动机间的同步误差。文献[14]将同步误差与位置误差平均值的差值作为耦合误差,改进了同步误差积分项,同时利用反演控制算法获得了较好的控制效果。文献[15]在同步补偿器中增加转速功率控制,将所有电动机的平均转速与各电动机间的转速差反馈至转速环,降低了各电动机间的同步误差。
上述文献主要针对多电动机在稳态运行中受到负载扰动时所采用的偏差耦合控制进行优化,但均未考虑多电动机传动系统启动过程中由于各电动机转动惯量不同造成的转速差。本文在传统偏差耦合控制的基础上增加转矩补偿器,根据各电动机转速与所有电动机平均转速之间的偏差,利用比例控制器对各电动机电磁转矩进行补偿,可提高系统启动过程和稳态受到扰动时的同步精度。
1 矿井带式输送机多电动机传动系统
某矿井长距离带式输送机多电动机传动系统如图1所示,其采用头部、中部和尾部3点驱动方式。为简化分析,每个驱动点各配置1台异步电动机,各电动机间连接方式等效为输送带柔性连接。由于带式输送机启动时间较长,且要求低速性能好,所以采用矢量控制变频器对异步电动机进行转速闭环控制。

图1 矿井带式输送机多电动机传动系统Fig.1 Multi-motor drive system of mine belt conveyor
假设所有电动机和配置的变频器参数完全相同,且无负载扰动时,只需给所有电动机施加同一时刻的启动信号和相同的给定转速,即可实现各电动机转速同步。然而实际系统无法避免随机的负载扰动,且电动机参数(如转动惯量)无法保证完全一致,上述因素会导致各电动机间的转速不同步,进而引起各电动机输出功率不一致、机械部件所受冲击大及输送带张力波动大等问题,降低带式输送机运行安全性和使用寿命。
2 基于偏差耦合控制的多电动机同步控制
2.1 传统偏差耦合控制
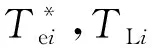
第i台电动机的同步补偿器结构如图3所示,将本电动机与第j(j=1,2,…,n,j≠i)台电动机的实际转速分别作差,然后乘以同步补偿器系数Kij(一般为本电动机与第j台电动机的转动惯量之比),相加后作为本电动机的输入补偿信号Δωi。
由图3可得同步补偿器i的数学模型:
(1)

图2 传统偏差耦合控制结构Fig.2 Structure of traditional relative coupling control

图3 同步补偿器结构Fig.3 Structure of synchronization compensator
2.2 带转矩补偿器的改进偏差耦合控制
传统偏差耦合控制中,各电动机之间的耦合度高。稳态运行中,任何一台电动机转速波动均会反馈给其他电动机进行同步补偿。其缺点体现在多电动机传动系统启动过程中:系统启动时转速控制器均处于饱和状态,同步补偿器失效,所有电动机具有相同的启动转矩;若转动惯量不同,则各电动机加速度不同,进而造成各电动机间不同步。
为解决上述问题,提出改进偏差耦合控制策略,如图4所示。
图4 改进偏差耦合控制结构Fig.4 Structure of improved relative coupling control

为保证较好的补偿效果,各转矩补偿器中的比例控制器参数应与对应电动机的转动惯量呈正比:
(2)

为保证系统安全,在进行转矩补偿后,还需给所有电动机设置相同的输出限幅,以防止变频器及电动机过载运行。
转速控制器为PI型,其传递函数为
(3)
式中:KPi,KIi分别为转速控制器i的比例系数和积分系数;s为拉普拉斯算子。
为简化分析,将每台电动机等效为积分环节[11],第i台电动机的传递函数为
(4)
第i台电动机实际转速由给定转速、负载扰动及其他电动机转速3个输入量决定。根据线性系统的叠加原理,分别对这3个输入量单独进行研究。
单独考虑给定转速对第i台电动机实际转速的影响,传递函数为
(5)
单独考虑负载扰动对第i台电动机实际转速的影响,传递函数为
(6)
单独考虑第j台电动机实际转速对第i台电动机实际转速的影响,传递函数为
(7)
综合式(5)—式(7),可得第i台电动机实际转速:
ωi(s)=G1i(s)ω*(s)+G2i(s)TLi(s)+
(8)
同时可得第i台电动机实际转速对应传递函数的特征方程:
(9)
式中D(s)为特征多项式。
将式(3)和式(4)代入式(9),可得
(10)
第i台电动机实际转速的稳态误差为
(11)
考虑负载扰动为阶跃突变时,TLi对第i台电动机转速产生的稳态误差为零,可将式(11)简化为
(12)
式中:t为时间;essj为第j台电动机实际转速的稳态误差。
由式(12)可得
(13)
式(13)为n阶线性方程组,且系数矩阵是非奇异矩阵,则式(13)存在唯一解,即
essi=essj=0
(14)
综合式(10)和式(14)可得:带转矩补偿器的改进偏差耦合控制系统是稳定的;所有电动机的稳态误差均为零,即每台电动机均可无静差地跟踪给定转速。
3 仿真验证
为验证带转矩补偿器的改进偏差耦合控制策略的正确性和可行性,根据图4所示的控制结构,以3台异步电动机M1—M3为例,在Matlab/Simulink中进行仿真。
仿真用异步电动机参数见表1。仿真条件:0 s时系统启动,3台电动机负载转矩均为10 N·m,给定转速为1 000 r/min;1.5 s时,3台电动机负载转矩均增大5 N·m;2 s时,3台电动机负载转矩均减小5 N·m。

表1 异步电动机参数Table 1 Parameters of asynchronous motor
将传统偏差耦合控制和改进偏差耦合控制进行对比仿真,结果分别如图5和图6所示。
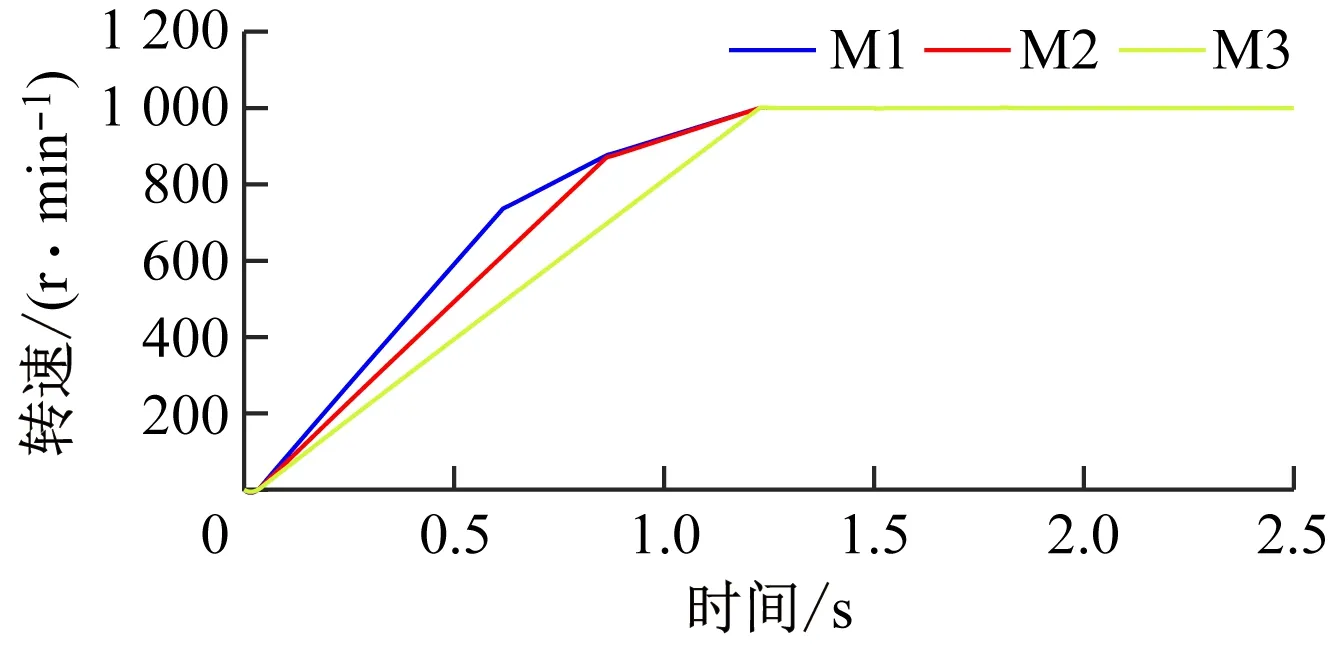
(a) 转速波形

(b) 稳态受扰时转速放大波形
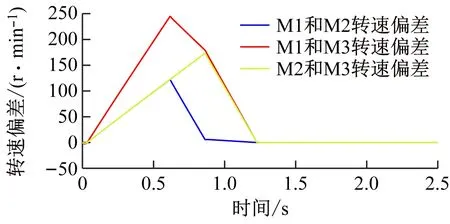
(c) 转速偏差波形
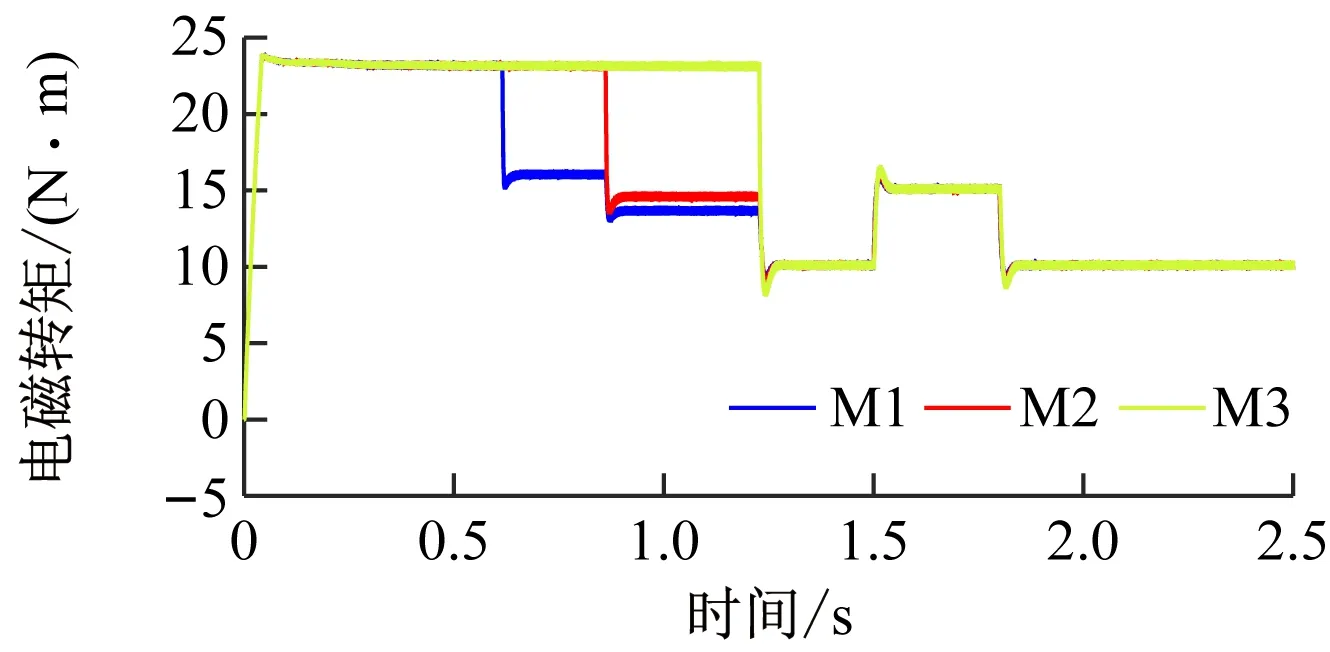
(d) 转矩波形图5 传统偏差耦合控制仿真波形Fig.5 Simulation waveforms of traditional relative coupling control
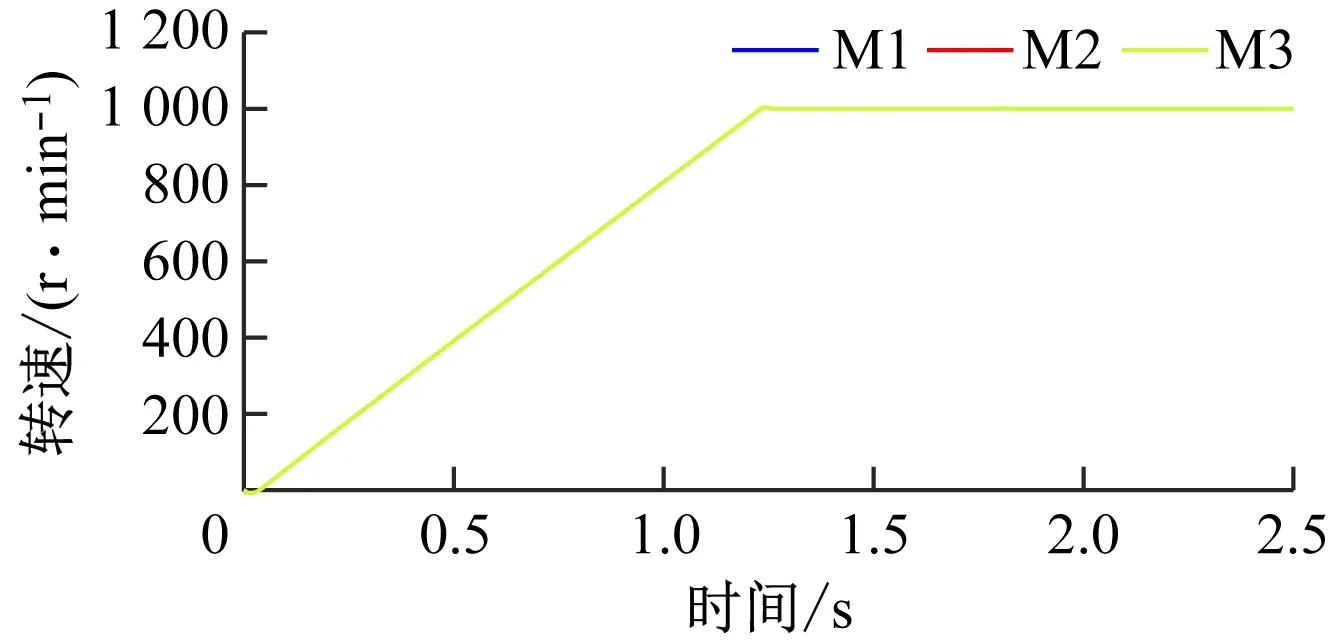
(a) 转速波形

(b) 稳态受扰时转速放大波形
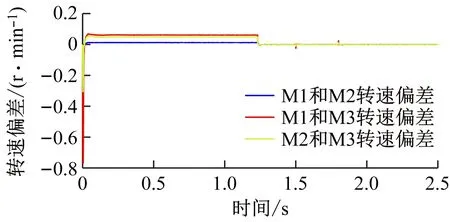
(c) 转速偏差波形

(d) 转矩波形图6 改进偏差耦合控制仿真波形Fig.6 Simulation waveforms of improved relative coupling control
对比图5和图6可看出:① 采用传统偏差耦合控制时,可保证多电动机传动系统稳态运行时的抗扰性能,系统在任一电动机受到负载扰动时均具有较好的同步精度;然而无法解决系统启动过程中由于各电动机转动惯量不同造成的不同步问题,其原因在于系统启动初始阶段,所有电动机的转速控制器输出饱和,同步补偿器失效,所有电动机均以相同的最大电磁转矩启动。② 采用改进偏差耦合控制时,在不影响系统快速性的基础上,可更好地提高系统稳态时的抗扰性能,各电动机在受到外部扰动时的同步精度更高;由于增加了转矩补偿器及转矩输出限幅环节,可补偿启动时各电动机所需的电磁转矩,进而保证所有电动机在启动阶段的转速同步。
4 实验验证
为进一步验证改进偏差耦合控制的性能,利用TMS320F28335 DSP进行硬件平台实验,3台异步电动机参数与仿真参数一致,且分别对拖1台直流电动机来模拟实际负载。
实验条件:启动时刻,给定转速为1 000 r/min,3台电动机负载转矩均为10 N·m;稳定运行后,3台电动机负载转矩均增大至15 N·m;再次稳定后,3台电动机负载转矩均减小至10 N·m。实验结果如图7和图8所示。

(a) 全过程转速波形
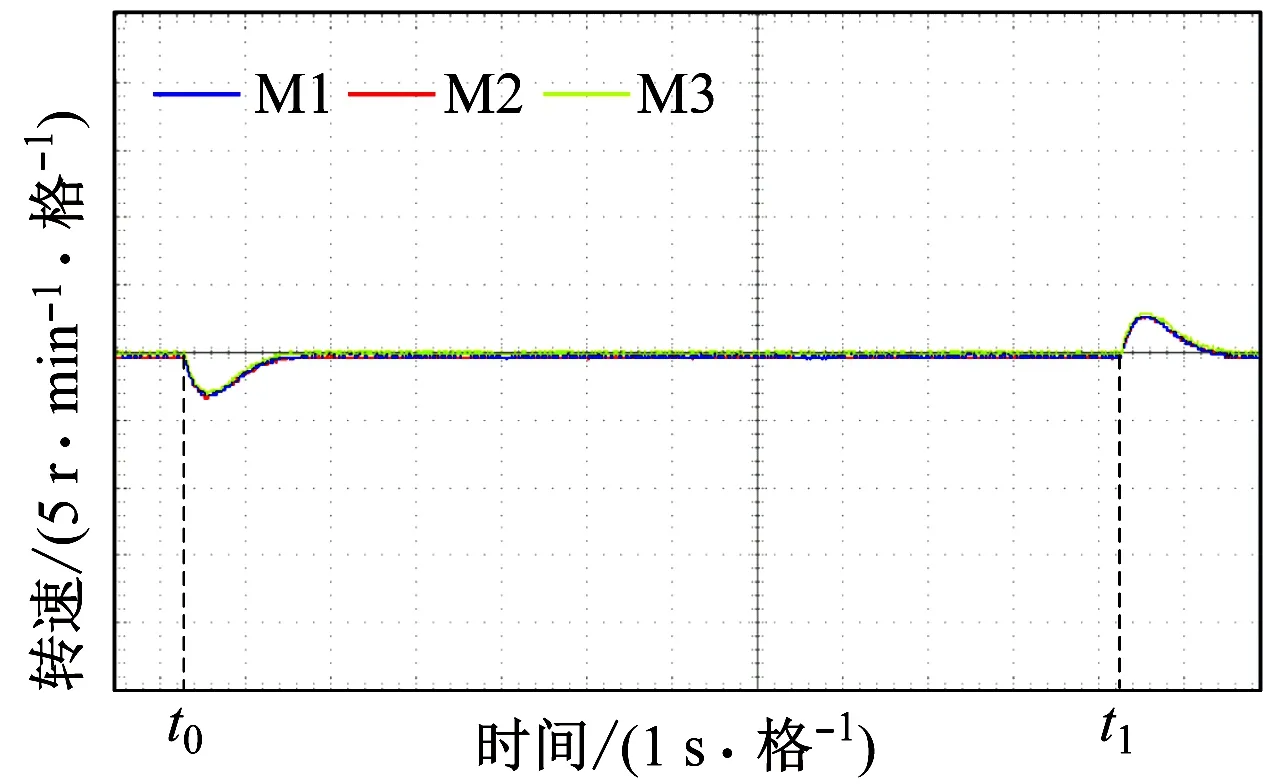
(b) 稳态受扰时转速波形图7 转速波形Fig.7 Waveforms of speed
(a) 全过程定子a相电流波形
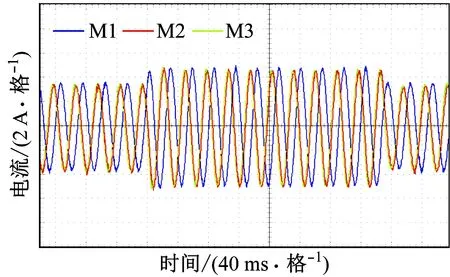
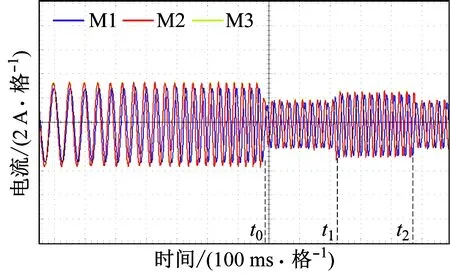
(b) 稳态受扰时定子a相电流波形图8 定子电流波形Fig.8 Waveforms of stator current
从图7可看出:不同转动惯量下的多电动机传动系统在启动和稳态阶段均可保持同步运行;稳态阶段3台电动机突加负载(t0时刻)和突减负载(t1时刻)时,系统抗扰性能较好,电动机受到扰动时的同步精度较高。
从图8可看出:由于增加了转矩补偿器,在启动阶段(t0时刻之前),转动惯量越小的电动机对应的电流越小;在稳定运行阶段(t0—t1),3台电动机电流相同;3台电动机突加负载(t1时刻)和突减负载(t2时刻)时,系统均可快速调节至重新稳定。
5 结语
以驱动点分散的矿井带式输送机多电动机传动系统为背景,针对传统偏差耦合控制无法解决不同转动惯量下多电动机传动系统的启动失步、稳态受扰时同步精度不高等问题,在传统偏差耦合控制中增加易实现的转矩补偿器,配合原有的转速控制器进一步对各电动机电磁转矩进行实时调节,并对各电动机补偿后的电磁转矩进行了相同的限幅。仿真和实验结果表明,带转矩补偿器的改进偏差耦合控制实现了不同转动惯量下多电动机传动系统在启动阶段的转速同步,稳态运行时的抗扰性能好且受到扰动后的同步精度高。

