融合深度神经网络的三峡库区滑坡灾害易发性预测

王 毅， 方志策， 牛瑞卿

(中国地质大学(武汉),湖北 武汉 430074)

中国三峡库区地质结构特殊,地形地貌复杂,人类工程活动较为频繁,滑坡等地质灾害广泛发育,对人类生命安全构成严重威胁,同时也给社会经济带来巨大损失[1]。滑坡灾害易发性预测是通过分析历史和现存滑坡灾害的空间分布,考虑研究区地形地貌、水文气象、基础地质等各类斜坡不稳定因素,对滑坡空间分布及其发生概率进行预测,能够为滑坡防治提供关键的科学依据。

根据理论基础的不同,滑坡灾害易发性预测方法分为定性和定量方法两大类[2]。前者主要依赖专家经验和研究人员对滑坡灾害的评估与分析能力；后者主要通过分析滑坡空间分布与滑坡影响因子之间的关系来预测可能发生滑坡的位置,包括确定性方法和数据驱动法。确定性方法通常基于无限斜坡模型开展滑坡易发性预测。Montgomery等[3]结合无限斜坡稳定模型与坡面水文模型建立了SHLSTAB模型,并将其用于田纳西河谷滑坡易发性预测。Pack等[4]将稳定态水文学理论融入无限斜坡稳定模型中,提出了稳定指数制图模型,并将其应用于温哥华流域易发性预测。在国内,兰恒星等[5]在稳定指数制图模型计算过程中增加动水压力项,将其应用于云南小江流域滑坡易发性预测。

数据驱动法在近些年来备受研究人员关注,包括频率比法[6]、证据权法[7]、逻辑回归(Logistic Regression,LR)[8]、支持向量机[9]和人工神经网络[10]等。深度学习作为当前人工智能领域的研究热点,在各个领域引起了广泛关注。其中,卷积神经网络(Convolutional Neural Networks,CNN)与循环神经网络(Recurrent Neural Networks,RNN)作为深度学习中两个最具代表性的方法,都具有强大的表征学习能力,已经被成功应用于图像处理、场景理解和自动驾驶等领域中[11-13]。随着三峡工程的建设,长期的地质灾害工作积累了大量地质资料与灾害数据,这类数据通常具有多源性、异构性、时空性、模糊性和非线性等特征,如何有效、充分地利用这些数据开展灾害管理防治工作是亟待解决的难题。此外,研究人员已将单个深度学习方法成功应用于滑坡灾害易发性预测,但其集成能力还未被挖掘。鉴于此,本文以长江三峡库区——秭归—巴东段(湖北省境内)为研究区,利用Stacking集成学习技术融合CNN与RNN来构建易发性评价模型,并将其应用于研究区滑坡灾害预测。

1 数据准备与分析

1.1 研究区背景

研究区位于湖北境内(图1),总面积达423.14 km2,地跨东经110°18′～110°52′、北纬30°54′～31°03′,最高海拔达到1 968.1 m。属亚热带季风气候区,年平均降雨量为1 100 mm,大部分降雨集中在5—9月,占年降雨量的70%。研究区地层发育较完整,除缺失泥盆系下统、志留系和石炭系上统和白垩系的大部分及第三系外,从震旦系至第四系皆有出露,总体上具有自东向西渐新展布的规律，岩性以灰岩、白云岩等碳酸盐岩和砂岩、泥岩、页岩等碎屑岩为主。研究区大地构造处于扬子准地台的中西部,是川东褶皱带、大巴山弧和淮阳山字形西翼反射弧的交汇区。褶皱和断裂对研究区的构造影响较大,其中褶皱发育有黄陵背斜、秭归向斜等，断裂主要有仙女山断裂、九畹溪断裂和香炉坪断裂。

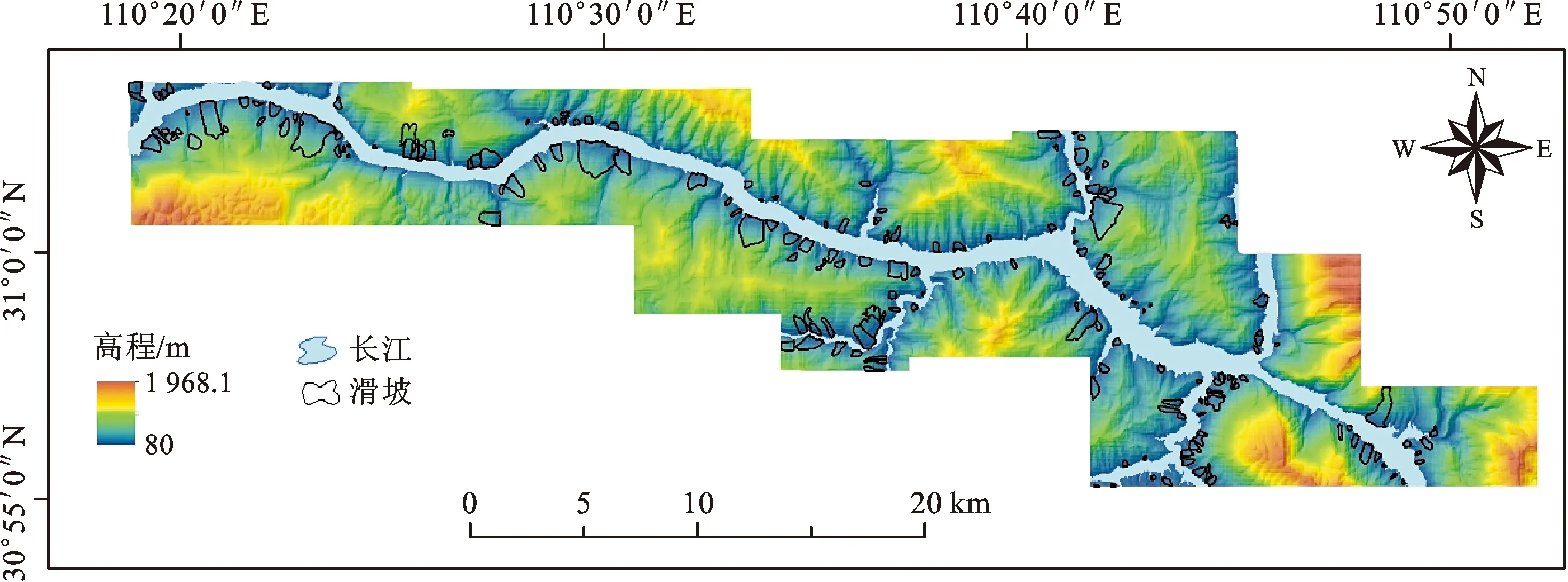
图1 三峡库区秭归—巴东段滑坡灾害分布图Fig.1 Distribution map of landslide locations in Zigui-Badong section of the Three Gorges Reservoir Region

近年来,人类工程活动对研究区的影响日益增大,包括移民城镇建设、水库建设、毁林开荒和矿山开采活动等。研究区主要的地质灾害类型包括滑坡、崩塌、塌岸和泥石流等,滑坡是区内发育数量最多的地质灾害,占其总数的83%。

1.2 滑坡数据编录

近年来,三峡库区库水位的周期性波动破坏了斜坡的稳定结构,导致了滑坡灾害的频繁发生。本文通过实地调查、Google Earth解译以及历史编录数据统计得到研究区滑坡编录数据(图1)。研究区共有196处滑坡,其中滑坡最大的面积为1.51 km2,最小的为172 m2。典型滑坡主要有黄土滑坡、黄蜡石滑坡、范家坪滑坡、新滩滑坡和千将坪滑坡等。

1.3 滑坡评价因子

评价因子的选取对于滑坡易发性评价至关重要。目前,研究人员在三峡地区开展了一系列滑坡灾害易发性预测研究[14-18]。因此,本文通过野外调查研究及已有相关研究,综合考虑研究区的地形地貌、基础地质、水文条件等因素,最终选取20个滑坡影响因子(图2)。为了保证这些因子的空间一致性,将这些因子图层重采样至相同空间分辨率。在此基础上,根据历史文献及专家经验对连续型图层进行重分类,再对所有图层子类别进行赋值。相关因子数据获取源如下：数字高程模型(digital elevation model,DEM)数据来自地理空间数据云ASTER GDEM v2版本数据(http://www.gscloud.cn/)；坡向、坡度、流域面积、流域坡度、曲率和斜坡形态因子通过ArcGIS软件从DEM数据中提取；地形位置指数(Terrain Position Index,TPI)、地形粗糙指数(Terrain Ruggedness Index,TRI)、地形表面曲率(Terrain Surface Convexity,TSC)、地形表面纹理(Terrain Surface Texture,TST)和地形湿度指数(Topographic Wetness Index,TWI)因子通过SAGA软件从DEM数据中提取；岩性和断层距离因子提取于湖北省地质局提供的地质图。降雨量因子来自2003—2010年雨量站点数据,震级因子来自1970年以来研究区及附近区域地震资料。通过地形图和遥感影像数据提取研究区水系网,再利用欧氏距离工具获得水系距离因子；利用支持向量机对2010年获取的Landsat-7卫星影像进行分类获得土地利用因子；利用ENVI软件波段计算工具获得植被归一化指数(Normalized Difference Vegetation Index,NDVI)和归一化水指数(Normalized Difference Water Index,NDWI)。

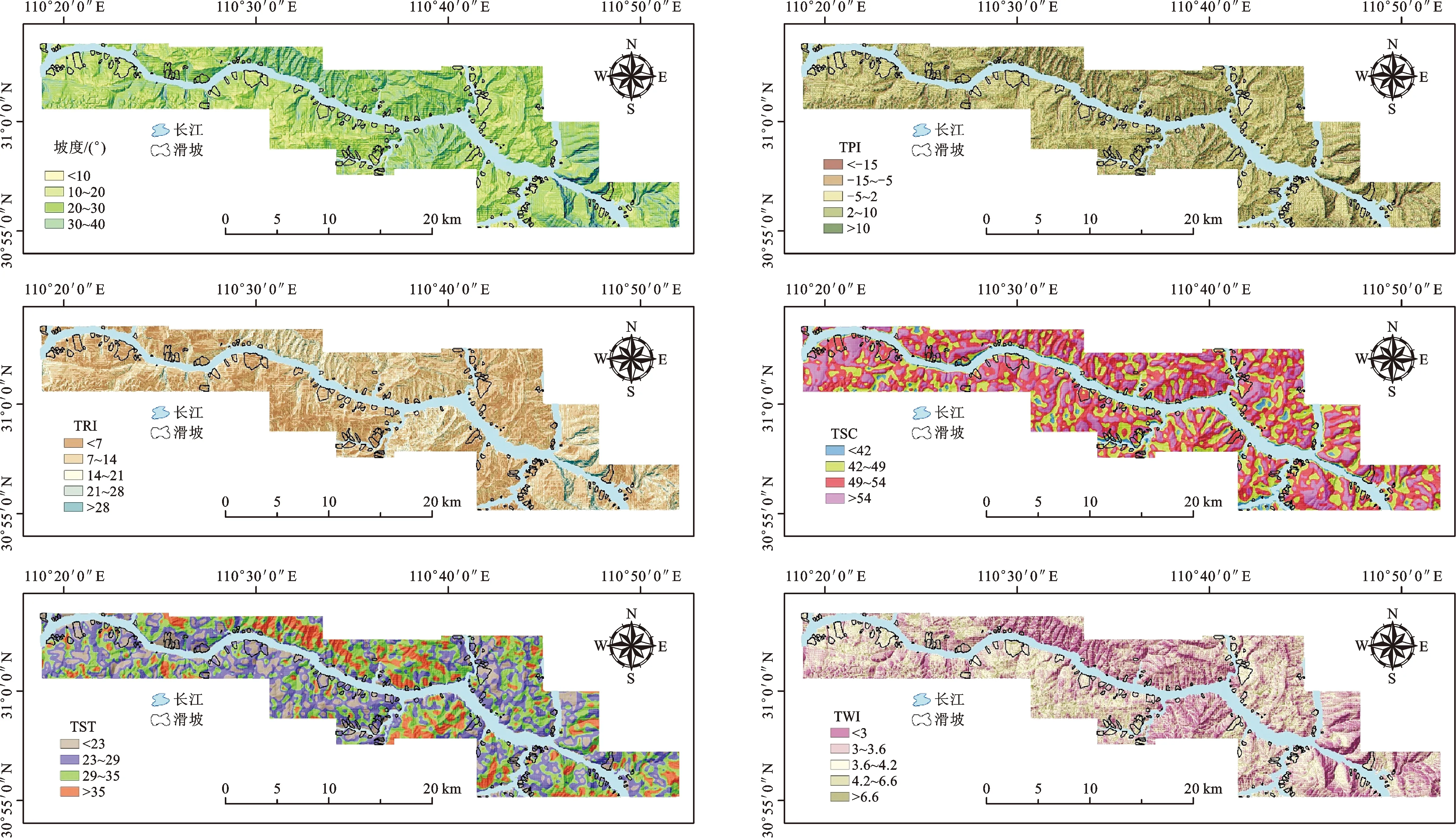
图2 滑坡影响因子专题图Fig.2 Thematic maps of landslide influencing factors

2 滑坡易发性评价模型

2.1 卷积神经网络

CNN最初是由LeCun等人针对手写数字识别而提出的一种特殊的神经网络模型[19],可用于处理具有已知网格拓扑结构的数据。CNN除了拥有与普通神经网络共有的输入层和输出层之外,其结构还包含卷积层、池化层和全连接层(图3)。

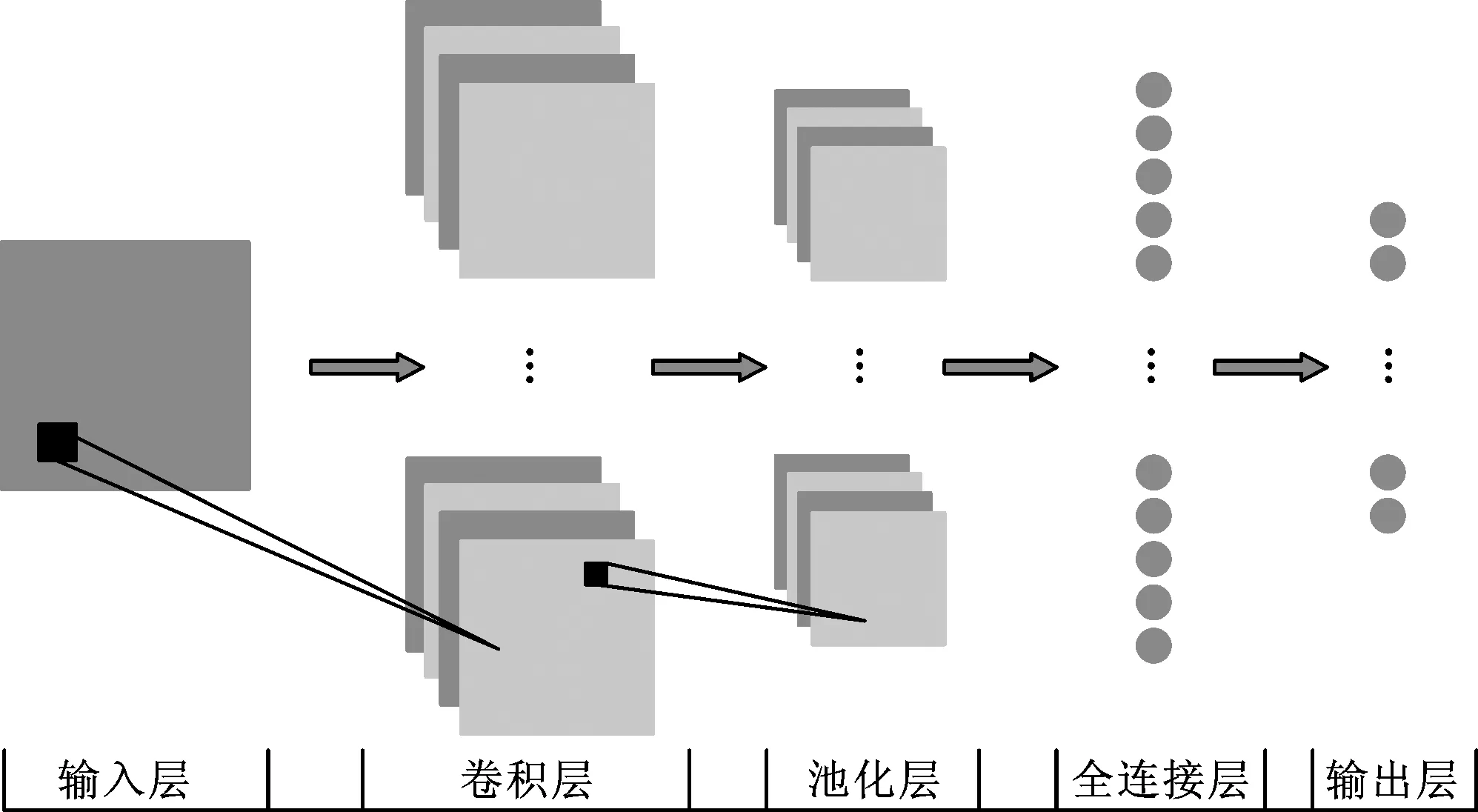
图3 典型CNN网络结构图[20]Fig.3 Typical network structure of CNN

如图3所示,卷积层中的卷积核可看作规则形状的滤波器,卷积窗口从输入数据的最左上方开始,按照从左往右、从上往下的顺序依次滑动,将其固定的权重与窗口内的数据做内积运算。卷积核在整个输入数据上完成一次卷积运算后会输出卷积特征图,即卷积操作所提取出的初级特征。以二维卷积为例,其计算公式如下：

(1)

式中：k为卷积核的个数；Cj表示第j个卷积核的输出；f表示非线性激活函数；i为卷积操作的位置；xi表示卷积窗口对应的输入数据；wj和bj分别表示权重和偏置。在卷积操作中,输入数据通常为多维数组,而卷积核则是通过学习算法不断调整固定大小的多维数组,这些多维数组被称为张量。

池化层中池化操作不仅能够通过降低卷积层输出特征图的维度来提高计算效率,还能使提取的特征保持平移不变性[21]。最常见的池化操作为最大池化,其计算公式如下：

(2)

全连接层也是CNN隐藏层中的一种,一般位于多个卷积层和池化层之后,其神经单元都与上一层的神经元相连。全连接层可看作为特殊的分类器,其目的是将卷积、池化操作提取出来的高维特征映射到低维特征空间。

2.2 循环神经网络

RNN考虑了输入数据之间的序列关系,并将“时间序列”引入了神经网络模型[22]。相比传统人工神经网络模型,RNN隐藏层中点的信息都能传递到下一个时间节点,因此数据中所蕴含的信息能够一直传递下去。本文构建了基于因子重要性排序的序列数据,利用因子选择方法对滑坡评价因子进行重要性赋值与排序,再将其输入到RNN模型中。如图4所示。假设x为输入的序列数据,时间步长t时的输出层为yt,它由当前节点的输入和上一节点共同决定,其计算公式如下：

图4 典型RNN结构图[23]Fig.4 Typical structure of RNN

ht=σ(Whxt+Uhht-1+bh)

(3)

yt=σ(Wyht+by)

(4)

式中：σ为激活函数；Wh和Uh为权重矩阵；b为偏置向量。

2.3 Stacking集成方法

Stacking集成是一种流行的异构集成学习方法,它通过使用元学习器将不同的基分类器组合在一起以获得更准确的预测结果[24]。与常用的Bagging和Boosting两种集成方法不同,Stacking用于集成不同类型的模型,而不是多个相同类型的模型。图5展示了Stacking集成的一般结构,该集成算法首先通过交叉验证的方式,使用训练基分类器未使用的样本来产生元学习器的训练样本。以5折交叉验证为例,初始训练集被划分为5个大小相同的集合D1,D2,…,D5。令其中一个集合为初级测试集,剩余的4个集合为初级训练集训练初级分类器,再利用该初级分类器对初级测试集进行预测,预测值作为元学习器训练集的一部分,重复5次得到元学习器的训练集。最后,利用该训练集训练元学习器并进行预测。Stacking集成方法可以通过初级学习步骤共同估计所有初级分类器的误差,并使用元学习步骤减少预测残差。

图5 Stacking集成结构图Fig.5 Structure of the Stacking ensemble

2.4 模型评价指标

本文选用总体精度(Overall Accuracy,OA)、精确率(Precision)、召回率(Recall)、马修斯相关系数(Matthews Correlation Coefficient,MCC)和一致性系数(Index of Agreement,IOA)这5个统计学指标评价模型。其中,精确率表示预测为滑坡的样本中有多少是真实的滑坡样本,召回率表示样本集中的滑坡样本有多少被准确预测[25]。MCC是一个较为均衡的评价指标,能够描述实际类别与预测类别之间的相关系数[26]。IOA是一种模型预测误差程度的标准化度量,它是由均方误差和潜在误差之比计算得到[27]。上述评价指标的公式如下所示。这5个评价指标的取值范围在0～1之间,其中取值越接近于1表示对应的模型性能越好。本文使用的另外一个评价指标为受试者工作特征(Receiver Operating Characteristic,ROC)曲线,它通过设定多个不同的临界值计算一系列敏感性和特异性,并基于这两个值绘制成曲线[8]。其曲线下面积(Area Under the Curve,AUC)可用来衡量模型的优劣。AUC值越高,表明该模型性能更优异。

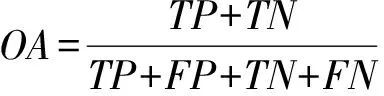
(5)

(6)

(7)

(8)

(9)

3 实验结果与分析

3.1 滑坡评价因子分析

根据历史研究及专家经验,初步选取的滑坡评价因子之间难免存在统计学上的共线性关系,这会导致易发性模型无法准确地分析评价因子与滑坡之间的真实关系。此外,影响滑坡因素众多,评价因子中存在的冗余信息可能会影响易发性结果的精度。因此,本文从共线性分析及重要性分析两个角度对滑坡评价因子进行定量评价与筛选。本研究区评价因子多重共线性分析结果如表1所示,其中VIF和TOL分别表示方差膨胀系数和容忍度[28],结果显示所有的滑坡影响因子之间不存在多重共线性。

表1 滑坡影响因子多重共线性分析结果Table 1 Multicollinearity analysis results of landslide influencing factors

此外,本文选用随机逻辑回归方法来定量分析滑坡评价因子的重要性。该算法对训练数据重采样并对每个样本应用L1惩罚逻辑回归模型以选择重要特征[29]。在多次迭代重复该过程后,如果始终选择某个特征,则该特征对于建模至关重要,而如果从未选择该特征则无关紧要。滑坡评价因子的重要性排序如图6所示,其中TWI相对其他因子而言对滑坡贡献最大,而坡向、斜坡形态和TPI因子重要性统计值为0,可视为无关因子而被剔除。因此,将剩余的17个评价因子用于后续的模型构建。

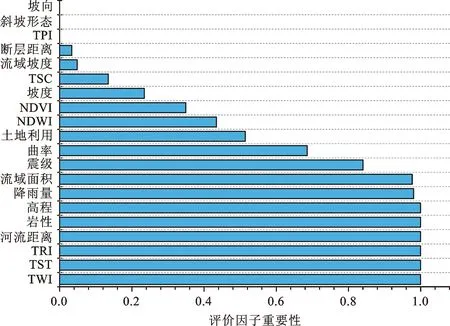
图6 滑坡影响因子重要性Fig.6 Importance of landslide influencing factors

3.2 模型构建

在进行滑坡易发性预测之前,需要选取训练样本和测试样本用于构建滑坡易发性模型,且训练集与测试集均由正样本(滑坡样本)和负样本(非滑坡样本)共同组成。由文中1.2节可知,研究区共有196处滑坡、25 380个滑坡栅格单元,从非滑坡区域随机选取25 380 个栅格单元作为负样本。为了探索滑坡易发性模型在滑坡样本非常有限的条件下的预测能力,从正样本和负样本中只随机选取10%的数据进行模型训练,而剩余的90%样本用于模型测试。

Stacking集成方法通过使用训练集集成CNN和RNN。首先,选择训练集的10%作为验证集来训练模型，CNN和RNN模型基于梯度下降算法迭代训练直到损失函数收敛(图7)。随着训练次数的增加,损失值减小直到达到一个低水平,这表明训练过程是令人满意的。然后,LR结合CNN和RNN的预测输出最终的分类结果。所使用的深度学习模型结构如下：CNN包含一个有着20个卷积核的卷积层、一个最大池化层和一个包含50个神经元的全连接层；RNN仅包含一个具有17个隐藏节点的循环层。此外,在实验中,相关的超参数是通过先前的研究和验证集的微调确定的[25,30],相关超参数如表2所示。

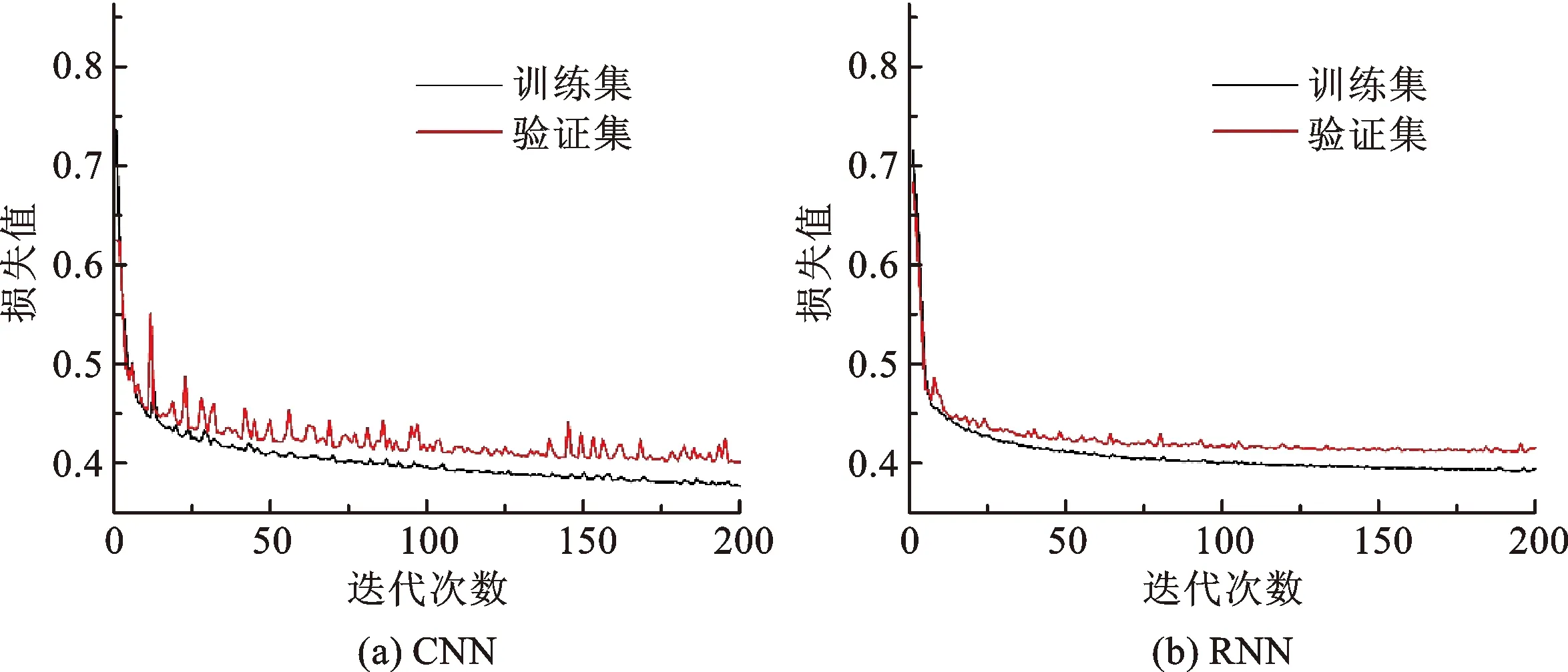
图7 训练过程模型损失值变化Fig.7 Change of loss value in training process model

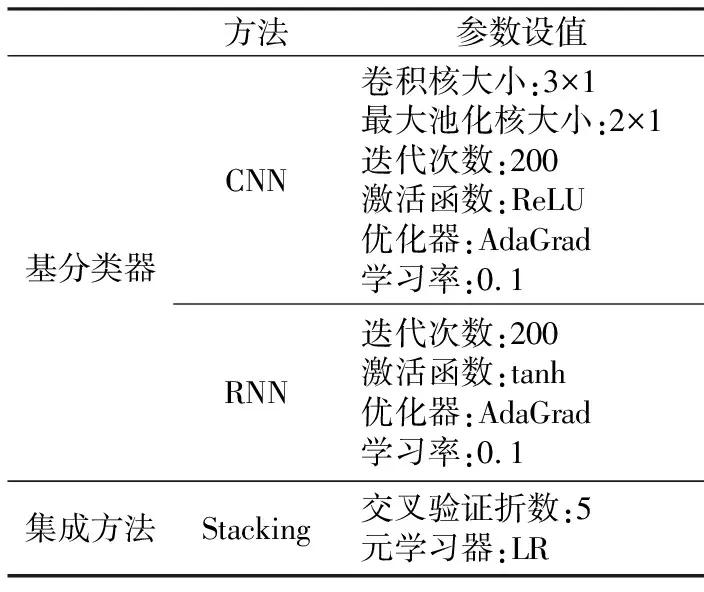
表2 模型超参数设置Table 2 Hyperparameter settings of the models

3.3 滑坡易发性预测图

为了评估Stacking方法的有效性,选择了CNN、RNN和LR这三种模型进行比较。本文使用自然断点法[6，9，17]将研究区划分为5个易发性等级,分别为极低、低、中、高和极高易发区。四种模型的滑坡易发性预测分区图如图8所示，可以看出四个分区图在空间分布上具有相似性，例如极高易发区主要分布在长江沿岸,大多数滑坡也都位于滑坡易发性极高区域。此外,四个分区图也存在少许差异，例如LR的中易发区分布(黄色区域)最多。

图8 滑坡灾害易发性预测分区图Fig.8 Prediction zoning map of landslide susceptibility

为了定量分析易发性分区图,本报告使用滑坡密度来衡量结果的可靠性和准确性。滑坡密度为易发性分区中滑坡比例与栅格个数比例的比值[31]。如表3所示,四种模型对应的易发性分区图中滑坡密度最高的为极高易发区,其次为高易发区、中易发区、低易发区和极低易发区。这与实际情况较为吻合,即滑坡往往更容易出现在极高易发区,而极低易发区滑坡出现的概率非常低。同时,从表3可以发现,Stacking的极高易发区滑坡密度在4种模型中最高,其次为CNN、RNN和LR，这说明Stacking模型预测的滑坡灾害高危区能够将历史滑坡包含在内,也证明了Stacking对研究区的易发性预测更为合理与准确。

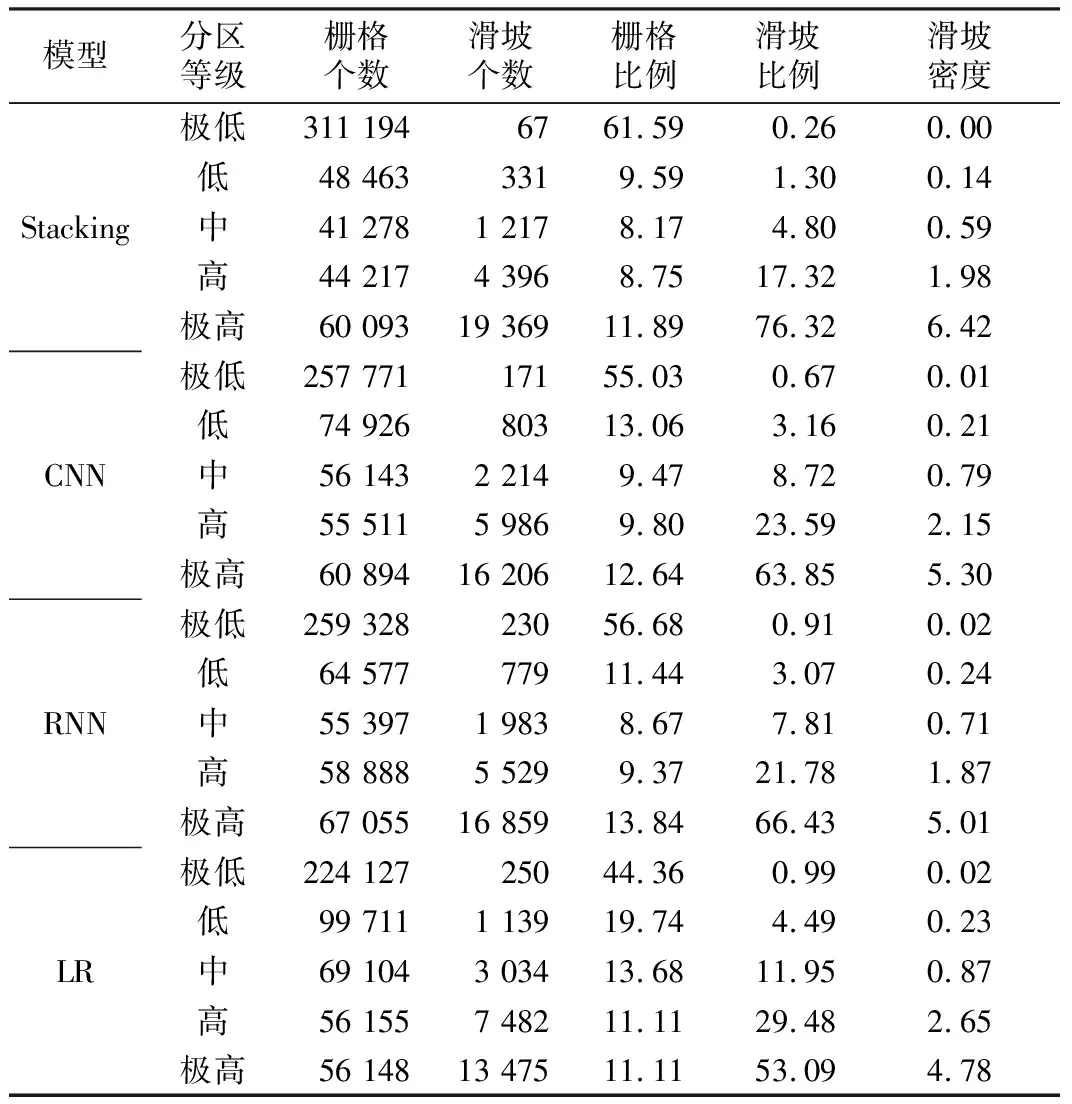
表3 模型各易发性分区滑坡密度Table 3 Landslide density of different susceptibility classes

3.4 模型比较与验证

四种模型的精度如表4所示，可以看出Stacking的精度最高,OA高达83%,比深度学习基分类器高出0.87%～1.61%；LR的精度最低,OA为80.11%。模型ROC曲线如图9所示，可以看出无论是基于训练集还是测试集,Stacking都能取得最高的AUC值,其次为CNN、RNN和LR。

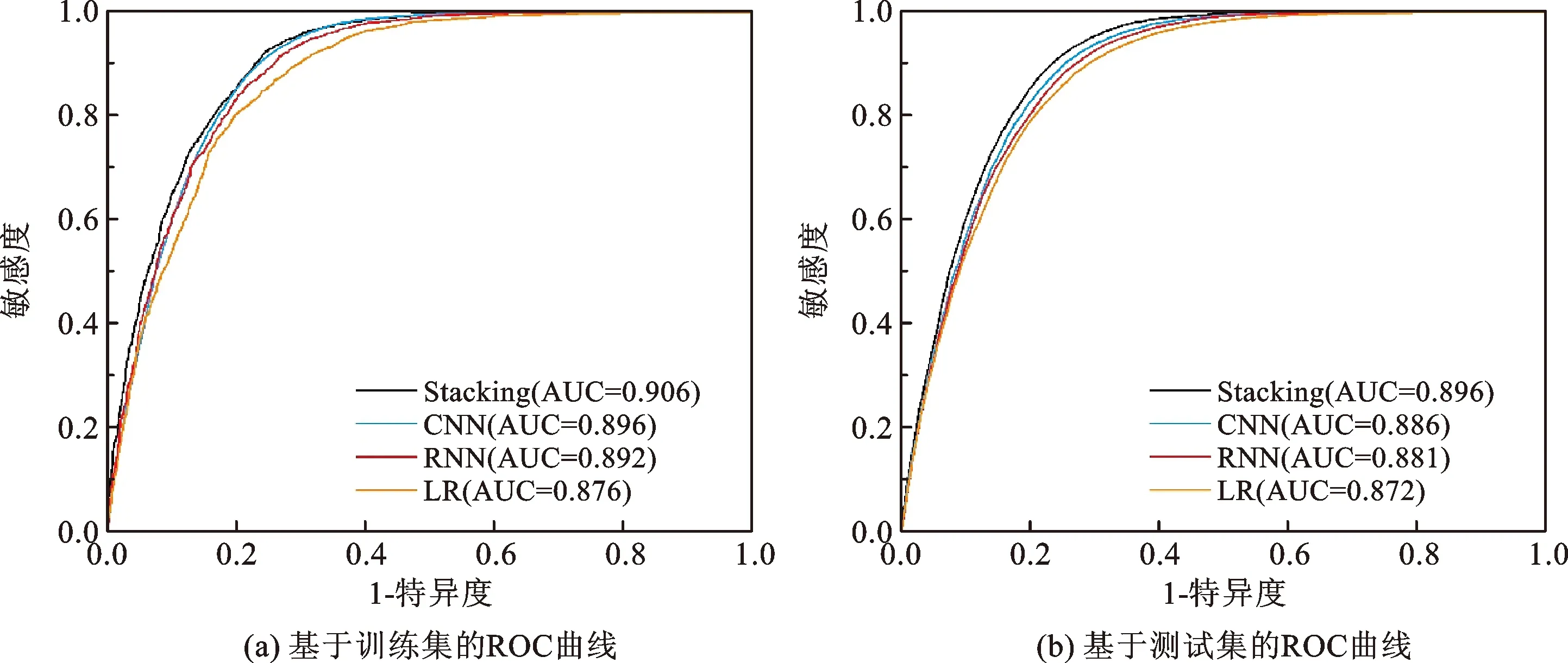
图9 模型ROC曲线Fig.9 ROC curves of different models

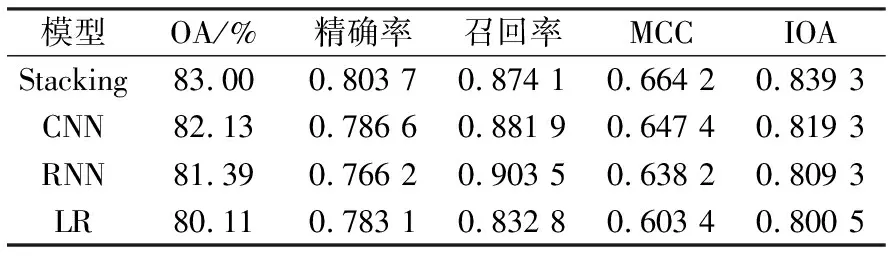
表4 模型精度评价Table 4 Performance of different models

4 结论

本文以长江三峡库首区——秭归—巴东段为例,选取高程、坡度、坡向、曲率、岩性等20个滑坡影响因子,利用Stacking集成策略融合CNN和RNN模型开展

滑坡灾害易发性预测。研究表明,Stacking集成学习可以充分利用基分类器的优点,拥有较好泛化能力和较高的预测精度。实验结果表明,Stacking集成方法在使用极其有限的样本进行建模时,能获得更为可靠的滑坡灾害易发性预测图,其预测总体精度为83%,皆高于CNN、RNN和LR。综上所述,本文不仅证明了Stacking集成在滑坡易发性预测有着巨大的应用潜力,也为深度学习集成模型的应用打下了基础。此外,深度学习在滑坡灾害易发性预测中的应用也存在超参数寻优较复杂的问题,解决这些问题并探索更有效的深度学习模型将是未来的研究目标。

致谢：感谢三峡库区地质灾害防治工作指挥部提供的相关实验数据和资料。