基于自适应模型预测控制的拖拉机路径跟踪研究

陆国强,许建秋

(1.三江学院 电子信息工程学院，江苏 南京 210012；2. 南京航空航天大学 计算机科学与技术学院，江苏 南京 211106)

路径跟踪控制作为拖拉机自主化作业的核心技术，可使拖拉机按照规划路径进行作业，提高作业质量和效率，降低驾驶员劳动强度[1-3]。拖拉机作业过程中的速度和跟踪路径曲率是不断变化的，有必要提高路径跟踪控制方法的自适应性，保证其自主作业精度。

目前用于拖拉机的路径跟踪控制方法主要包括PID控制、纯跟踪控制、模糊控制、模型预测控制等[4-7]。PID 控制无需构建车辆模型，易于实现，但参数整定较难，为提高其鲁棒性，将模糊控制和神经网络与PID相结合[8-9]。纯跟踪控制是根据当前的位置偏差、航向偏差和车辆几何学模型求得控制输入，其结构简单，实现方便，被广泛应用。基于纯跟踪控制的路径跟踪效果的关键在于参数前视距离的选取，而作业速度和跟踪路径曲率对该参数的选取影响较大，模糊控制被用来自适应调整前视距离，提高其跟踪精度[10-11]。模型预测控制(MPC)是基于预测模型、滚动优化和反馈矫正的控制策略，具有较强的鲁棒性，且在优化求解过程中可考虑控制量、控制增量等约束条件[12-14]。

考虑到拖拉机作业过程中，控制信号会由于信号通讯、执行器等造成一定的延迟，使得当前时刻产生的控制信号在未来时刻被执行，而MPC是一种预测控制，可有效补偿延迟问题。本文采用了基于MPC的路径跟踪控制方法。文献[15]指出了MPC中预测时域对跟踪效果影响较大，当速度和跟踪路径发生变化时，应对其适当调整。文献[16]设计了自适应MPC控制器，根据参考轨迹曲率的变化自动调节预测时域，但并未考虑速度变化时对预测时域的调整。本文针对拖拉机作业速度和路径曲率变化时，基于固定预测时域MPC控制器的跟踪效果可能变差的问题，提出一种自适应MPC控制器。当作业场景变化时，利用改进的粒子群优化(PSO)算法求取最优的预测时域，保证路径跟踪控制器的鲁棒性和精确性。

1 拖拉机运动学模型

由于拖拉机的作业速度低，模型预测控制通常可采用结构简单、易于建模的运动学模型。假设拖拉机左右对称，四轮车模型可简化为二轮模型，拖拉机模型示意图如图1所示。在导航坐标系下，得到拖拉机的运动学模型为

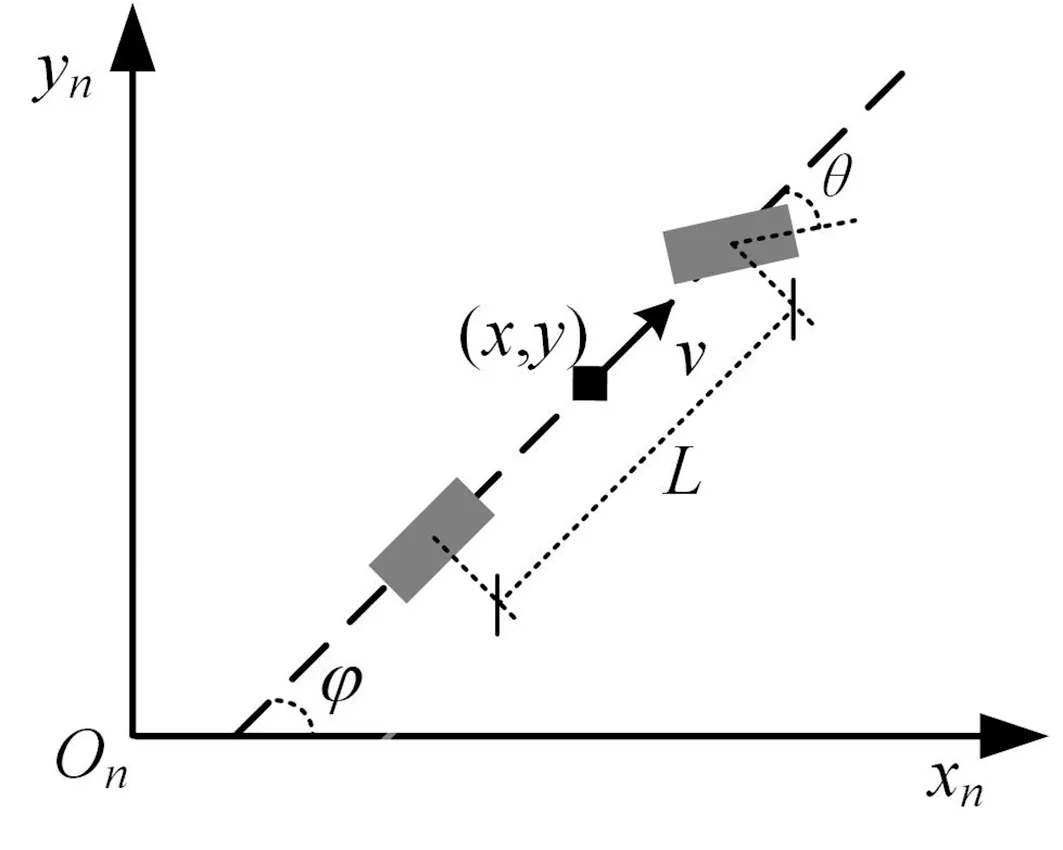
图1 拖拉机模型示意图

(1)

式中：x，y为拖拉机的质点在导航坐标系下的坐标；φ为航向角；v为纵向速度；θ为车轮转向角；L为前后轮轴距。

路径跟踪控制器中采用的误差量为系统状态变量，基于式(1)的线性化和离散化处理，可得该系统的状态空间方程为

(2)

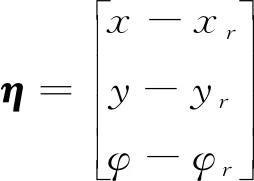
控制输入会由于信号通讯、执行器等造成一定的延迟，则状态空间方程表示为

(3)

式中kd为输入延迟时间，可通过试验测量获得。

考虑到本文是为了验证拖拉机在不同作业速度和跟踪路径时，所提出的基于自适应预测时域的MPC效果，忽略了输入延迟，采用基于式(2)的状态空间模型。

2 自适应路径跟踪控制器设计

MPC是根据当前时刻传感器测量的拖拉机状态信息与期望值的偏差，并通过优化求解得到控制输入来改变拖拉机的运行状态，进而实现路径跟踪效果。MPC模型的初始化参数中的预测时域P对其解算结果的影响较大，当拖拉机的速度或跟踪轨迹有较大变化时，路径跟踪效果会受到影响，故本文采用了改进的粒子群优化算法对预测时域P进行适当调整。基于自适应MPC的路径跟踪控制算法如图2所示。

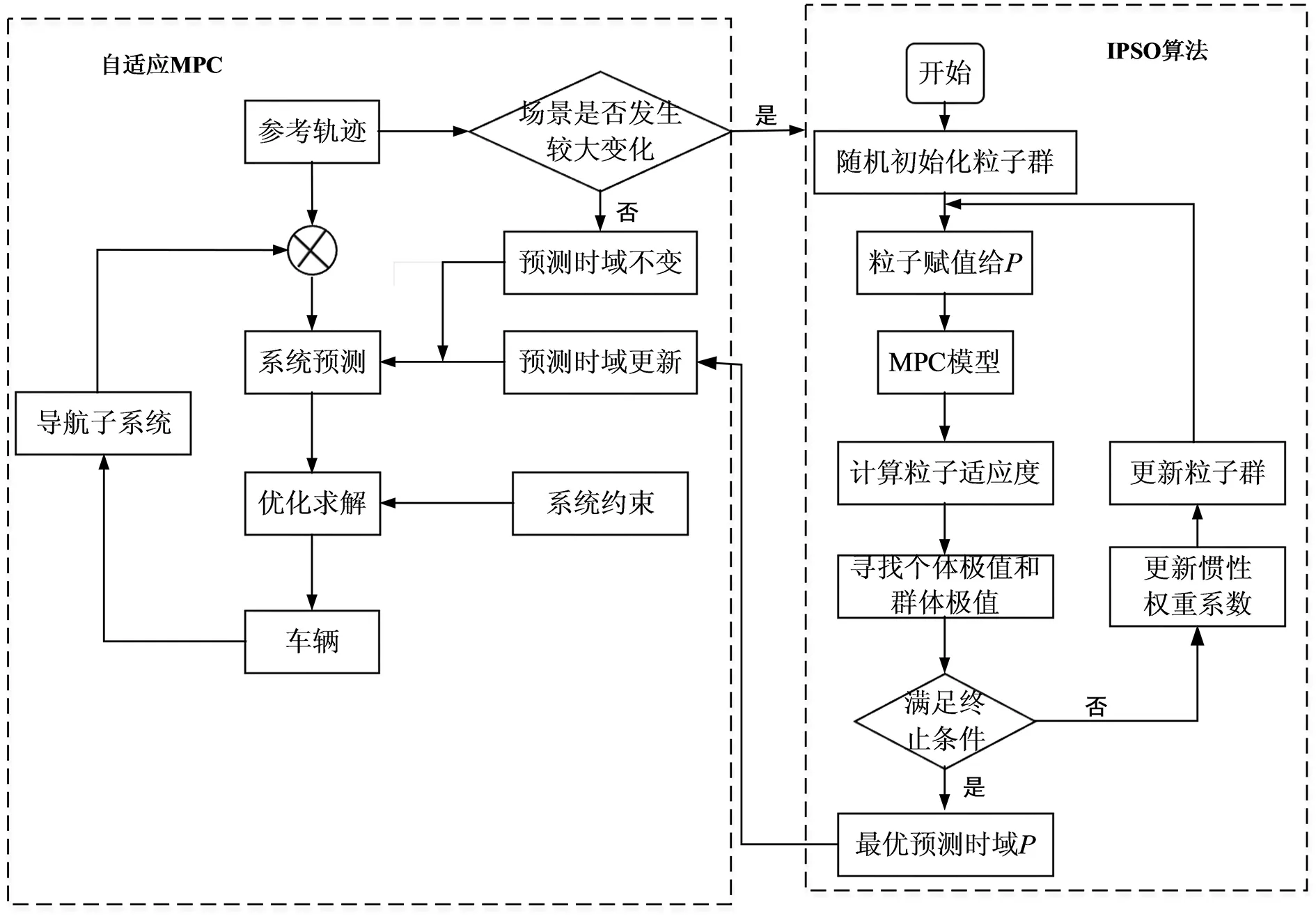
图2 基于自适应MPC的路径跟踪控制算法

2.1 模型预测控制

MPC是结合拖拉机运动学模型、当前状态预测之后的优化控制值，可在一定程度上补偿控制器的延迟，且根据需要增加一定的约束条件。

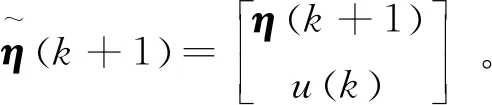
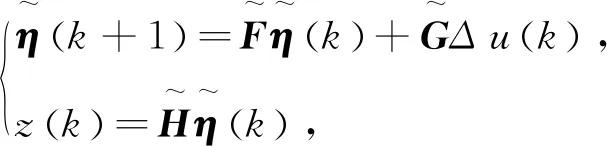
(4)

假设预测时域为P，控制时域为C，则Δuk+C-1=Δuk+C=…=Δuk+P-1。根据上式可得时刻k的预测输出为

(5)

令时刻k的控制序列为ΔUk，输出序列为Zk+1，则：

模型预测控制的评价函数为

(7)

MPC的约束条件设置为

(8)

式中：umin和umax为控制量约束值；Δumin和Δumax为控制增量约束值。

通过优化求解，可得控制时域内时刻k的控制输入增量ΔUk，则时刻k的控制输入量为

uk=uk-1+Δuk。

(9)

2.2 改进粒子群优化算法

拖拉机作业过程中速度和跟踪路径是变化的，若模型预测控制中的参数设定为固定值，路径跟踪效果会受到一定的影响。为了提高路径跟踪的自适应性，采用改进粒子群优化算法，根据工作场景对预测时域进行优化选取。

PSO算法中粒子的速度和位置更新轨迹为[17]

(10)

式中：Vj为粒子j的速度；Xj为粒子j的位置；w为惯性权重；c1、c2是加速度常数；r1、r2是随机数；Xj,p为该粒子经过的最优位置；Xj,g是整个种群中粒子经过的最优位置；m是群体规模。

参数w反映了对全局和局部搜索的权重，对于PSO算法的寻优过程尤为重要。为了提高寻优性能，对传统的粒子群优化算法进行改进，将w设定为分段函数，第k次迭代的惯性权重值wk为

(11)

式中：Iλ为转折迭代次数；Imax为最大迭代次数；wλ是转折权重值；wmax是最大惯性权重值；wmin为最小惯性权重值。

3 仿真实验与分析

为了验证本文算法有效性，针对拖拉机不同的作业速度和跟踪路径，分别对基于固定预测时域和自适应预测时域的MPC控制器进行仿真实验和对比分析。选用东方红-X1304拖拉机为仿真实验对象，其前后轮轴距L为2.688 5 m。MPC控制器的相应参数设置是：采样周期为T=0.05 s，控制量约束值分别为umin=-0.523 6 rad、umax=0.523 6 rad，控制增量约束值分别为Δumin=-0.087 3 rad、Δumax=0.087 3 rad，控制时域为C=5。粒子群优化算法的相应参数是：加速度常数为c1=c2=1.494 55，最大惯性权重值为wmax=0.9，最小惯性权重值为wmin=0.4，转折惯性权重值为wλ=0.6，转折迭代次数为Iλ=5，种群规模m=10，最大迭代次数Imax=50。

3.1 直线跟踪路径

直线作业是拖拉机较普遍的作业方式，对作业速度v分别为1、2 m/s和变速v=1.5+0.5sin(2πt/30)，采用基于不同固定预测时域值和自适应预测值的MPC控制器进行仿真实验。初始位置偏差设定为3 m，初始航向偏差为π/3 rad。图3给出了跟踪直线路径时，不同作业速度下的跟踪路径、航向角跟踪误差和控制输入结果图。从图3可以看出，同一预测时域在速度不同时，预测效果不同，如预测时域P为10时，若速度为1 m/s效果较差，若速度为 2 m/s效果较好；控制输入都在设定的约束条件内，且基于自适应预测时域的MPC控制器的控制输入波动小，收敛速度快；基于自适应预测时域的MPC控制器在三种速度情况下，跟踪效果都优于基于三个固定预测时域的MPC控制器。

3.2 曲线跟踪路径

为了验证跟踪不同路径的控制器效果，对曲线路径进行仿真实验验证。曲线跟踪路径半径设定为20 m的圆弧，初始位置误差为3 m，初始航向偏差为0 rad。作业速度v分别为1、2 m/s和变速v=1.5+0.5sin(2πt/30)，跟踪路径、航向角跟踪误差和控制输入结果如图4所示。从图4可以看出，拖拉机可以有效跟踪曲线路径；对于基于固定预测时域的MPC控制器，在速度不同时，最优预测时域不同，如速度为1 m/s时，预测时域为30要优于其他两个固定预测时域值，而速度为2 m/s时，预测时域为20的控制器效果较好；三种速度下，基于自适应预测时域的MPC控制器的跟踪效果都优于基于三种固定预测时域的MPC控制器。

(a) v=1 m/s

为了进一步分析算法的有效性，对跟踪误差均值和收敛时间进行了统计分析，其结果分别见表1和表2。其中，跟踪误差用行驶轨迹上的点到离期望路径最近点的距离评价，收敛时间用跟踪误差收敛到0.05 m以内的时间统计。表1表明，在基于固定预测时域的情况下，速度越小，预测时域的值设定为较大值时跟踪误差越小，而速度变大时，应适当减小预测时域；不同作业速度和跟踪路径的工作场景中，基于自适应预测时域值的跟踪误差相对于其他固定时域的降低了2%～44%，跟踪精度更高。表2表明，同一预测时域在速度或跟踪路径不同时，收敛效果不同，如预测时域P为20，跟踪直线路径时，若速度为1 m/s收敛速度要优于预测时域为30和10，若速度为 2 m/s收敛速度最慢；跟踪曲线路径时，若速度为1 m/s收敛速度居中。不同作业速度和跟踪路径时，基于自适应预测时域值的收敛时间相对于三种固定时域下的收敛时间缩短了2%～71%，收敛速度最快。

表1 跟踪误差均值统计

表2 收敛时间统计

4 结束语

针对基于固定预测时域的MPC控制器，为提高控制器的自适应性，本文结合工作场景和PSO算法对预测时域进行适当调整，并采用分段函数的惯性权重对PSO算法进行了改进。以东方红X-1304拖拉机为仿真对象，分别对不同速度和路径情况进行了实验验证和对比分析。实验结果表明，相比于基于固定参数的MPC控制器，自适应MPC控制器在不同工作场景下都具有较好的路径跟踪效果。该路径跟踪技术可提高拖拉机自主化作业的环境适应性，为后续试验提供研究基础。