多采样率牵引传动控制系统中的电流环建模

田 鑫，王琛琛，周明磊，王 剑

（北京交通大学电气工程学院，北京 100044）

0 引言

数字控制系统是一个内部既含有连续时间信号又含有离散时间信号的混合系统，系统中的连续时间信号与离散时间信号分别通过采样器与保持器进行互相转换。如果系统中所有采样器、保持器都以相同的周期同时动作，则称这样的系统为单采样率系统，简称为单率系统。如果系统中含有两个及以上有着不同工作周期的采样器与保持器，称这样的系统为多采样率控制系统，简称为多率系统[1]。

随着数字控制技术的发展，多采样率控制已被广泛应用于自动化制造、信号处理、航天航空以及机器人控制等领域。对于多采样率控制的研究也已经持续多年，并且产生了一系列成果：Kranc[2]提出了开关分解法，在频域获得了多采样率系统的等效脉冲传递函数模型；Jury等[3]证明了对于周期时变的离散时间系统，如果从那些等于其周期整数倍的采样时刻来看，是时不变的；Kalman等[4]采用状态空间方法描述了多采样率系统。在此基础上经Araki等[5]、Godbout等[6]的逐渐发展，利用 “提升”技术获得多率系统的等效单采样率状态空间模型渐渐成为对多率系统的主要分析方法。

在大功率的牵引传动控制系统中，为了提升电流环的动态性能，已有文献结合多采样率控制提出了一些高性能的控制算法[7-10]。然而，大多数文献只是将单采样率控制下的控制算法拓展到多采样率下，对多采样率控制下系统的数学模型、特性等理论分析不足，多采样率控制下电流环的设计存在较大挑战。

本文对多采样率牵引传动控制系统中的电流环进行了分析。首先介绍了多采样率控制下的系统结构，然后运用 “提升（Lifting）”技术分别获得了理想情况下多采样率控制下负载与电流调节器的状态空间模型，进而建立了系统电流环的等效单采样率闭环状态空间模型。为了使理论模型更加准确，分析了多采样率下系统电流闭环中的延时以及延时的影响并完善了系统模型。最后，利用Matlab／Simulink仿真验证了本文所建立理论模型的正确性。

1 多采样率系统结构

1.1 永磁同步电机连续时间状态空间方程

在两相同步旋转坐标系下，可以得到永磁同步电机的电压方程

式（1）中，ud、 uq分别为定子 d轴、q轴的电压，id、iq分别为定子d轴、q轴的电流，Rs为定子电阻，ωs为电角速度，Ls为电机的定子电感，ψf为永磁体磁链，ωsψf为永磁体反电势。由于永磁体产生的反电势ωsψf与定子电流无关，在磁链估计准确时可以被完全补偿，因此将式（1）中永磁体反电势项ωsψf忽略，可以得到状态方程

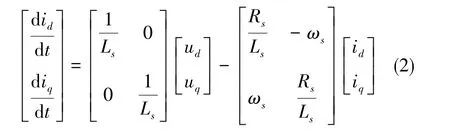
由式（2）可以获得永磁同步电机的连续时间状态空间模型

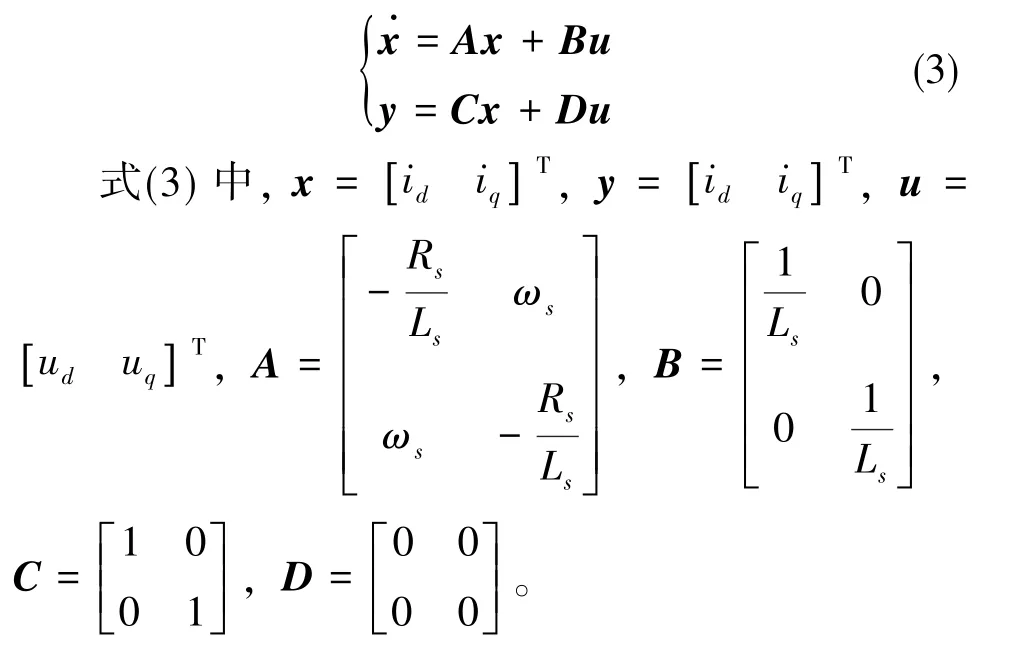
1.2 电流环结构

考虑到忽略永磁体反电势项后的永磁同步电机状态空间模型与三相对称阻感负载的状态空间模型是相同的，因此本文所研究的多采样率牵引控制系统中的电流环结构如图1所示。

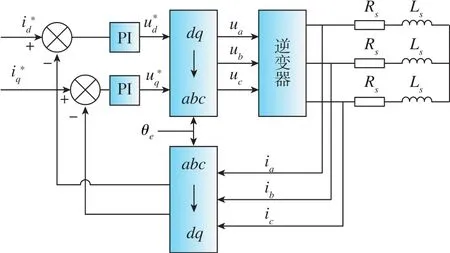
图1 电流环结构示意图Fig.1 Schematic diagram of current loop structure

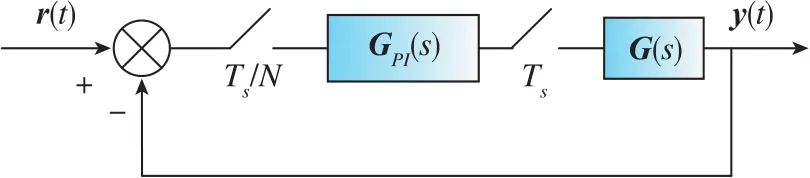
图2 系统框图Fig.2 Block diagram of system

图2中，r（t）为参考输入， 在本系统中对应d轴、 q 轴指令电流； GPI（s）、 G（s）分别为同步旋转坐标系下PI控制器与负载的连续时间传递函数。对于上述系统而言，从负载的角度分析，系统属于输出多采样率系统，N为系统的输出采样重数[10]。

2 多采样率下电流环建模

对于一般的多采样率数字控制系统，为了简化分析，常常使用两个假设：一是假定系统中存在一个基本采样周期T，系统中各采样点的采样周期都是T的整数倍；二是同时性假定，即假定系统中所有采样开关在同一起始时刻开始采样。在这两个假设下，可以利用 “提升”技术得出系统的线性时不变模型[1]。为了获得多采样率下牵引传动系统的电流环模型，本节利用 “提升”技术先分别获得负载与电流调节器的状态空间模型，进而推导出电流环的闭环模型。

2.1 多采样率下负载状态空间模型

对于多采样率系统，定义系统中所有周期的最小公倍数T0为系统帧周期，以帧周期分析系统，系统可以看作是线性时不变的。在本文研究的系统中，易知系统帧周期T0=Ts，并且系统基本采样周期为ΔT=T0／N。

对于连续时间状态空间方程，可以使用零阶保持器对其进行离散化。结合式（3）所表示的负载连续时间状态空间模型，以帧周期T0进行离散化，可以得到单采样率下系统状态空间模型

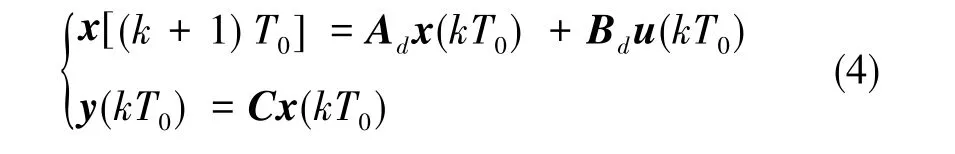
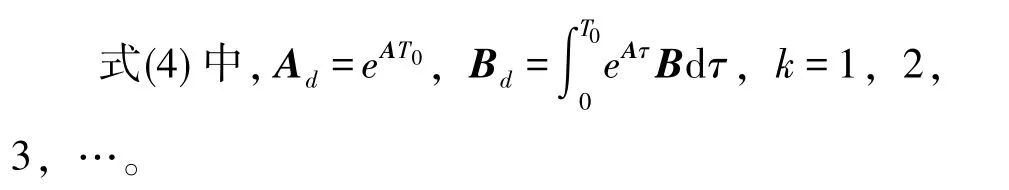
考虑多采样率控制下负载的离散状态空间模型，由于在一个帧周期内负载的输入电压u保持不变，因此多采样率下负载的状态方程与式（4）中相同。但是对于负载的输出方程而言，由于多采样率控制，系统在一个帧周期内进行了N次等间隔采样，获得了更多时刻的电流采样值。为了获得此时的负载输出方程，对于这N次采样而言，根据线性系统理论，可以先得到如下所示的状态转移方程

结合式（4）中负载的输出方程与多采样率下的状态转移方程（式（5）），并消除中间采样时刻的状态，可以获得多采样率控制下的输出方程，有

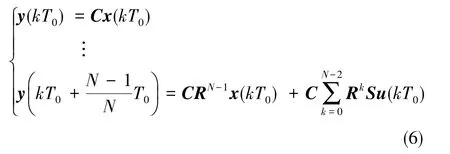
观察式（6），等号左侧为对负载输出N次采样的结果，等号右侧为负载在kT0时刻的输入u（kT0）与状态x（kT0）的线性组合。此时利用 “提升”技术，定义扩展输出变量

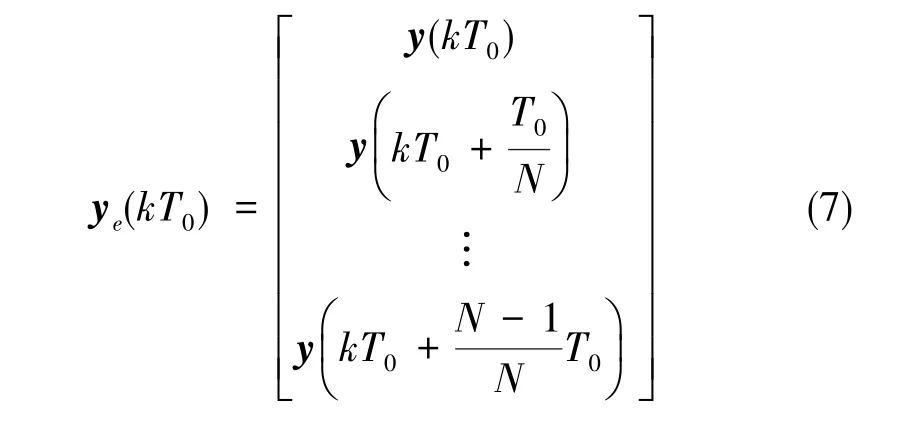
则负载的输出方程可以写为

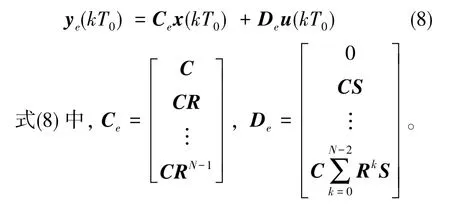
综上，负载在多采样率控制下的状态空间模型可以表示为

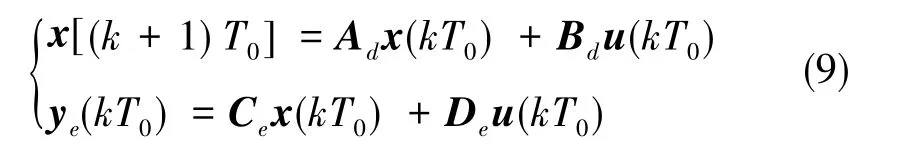
式（9）中，所有变量的采样周期都是帧周期T0。换言之，通过这样的方式获得了负载的等效单采样率状态空间模型。

2.2 多采样率下电流调节器状态空间方程

在本系统中，电流调节器选择PI控制器。考虑到由于数字实现，实际电流调节器的输出存在ΔT的采样计算延时[7]，则在连续域下的PI控制器如图3所示。

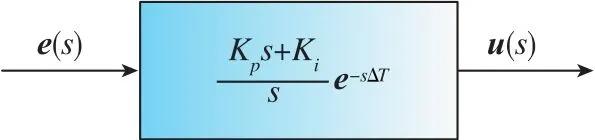
图3 PI控制器Fig.3 Diagram of PI controller

图3中， e（s）、 u（s）为 PI控制器输入、 输出的拉氏变换，Kp、Ki分别为控制器参数。为获得在多采样率下控制器的状态空间模型，先将如图3所示的PI控制器以基本采样周期ΔT进行离散化，可以获得离散的状态空间方程

2.3 系统闭环模型

结合式（9）、 式（15）， 可以获得多采样率控制下系统电流环的闭环模型

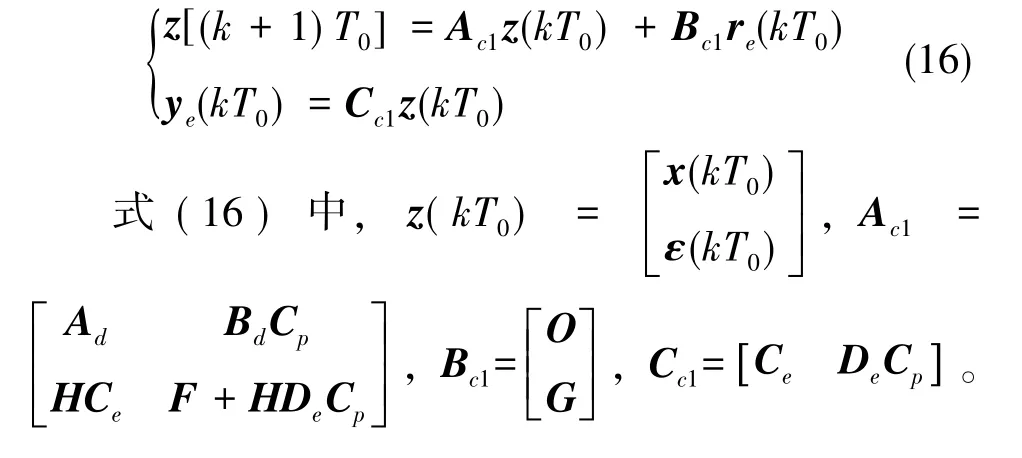
3 电流环延时分析

数字延时在同步旋转坐标系下可以分为角度延时与时间延时两部分[11]。在前一节的推导中，本文只考虑到了数字延时的时间延时部分，而没有考虑到角度延时的影响，这使得理论模型不够准确。在本节中，首先详细分析了多采样率下电流环中的延时环节，然后分析了角度延时对电流环的影响，进而获得准确的多采样率下的电流环模型。

3.1 电流环延时分析

在本文所应用的多采样率控制中，电流采样模式如图4所示。在一个开关周期Ts内进行多次采样、计算，PWM环节每次更新占空比信号都采用最近的一次计算结果。

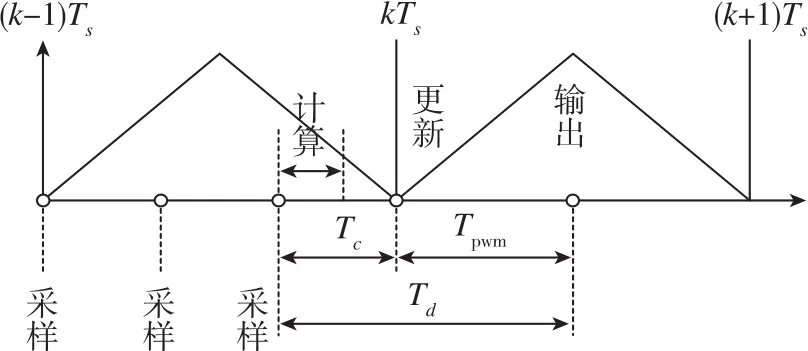
图4 采样模式示意图Fig.4 Schematic diagram of sampling mode

在图4所示的采样模式下，电流环的采样延时为

同时，PWM环节等效为零阶保持器，PWM输出延时为

因此在多采样率控制下，系统电流环总延时为

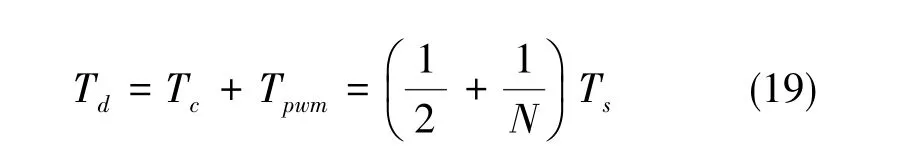
3.2 延时影响分析

由前述可知，在多采样率控制下系统电流环总延时为Td，本节考虑在延迟时间Td内角度延时对实际输出电压的影响。根据复矢量理论，可以将静止坐标系下和旋转坐标系下的电压矢量用复矢量的形式表示[12]，相应的两相旋转与三相静止坐标系之间的坐标变换可以表示成（θe为电压矢量角度）

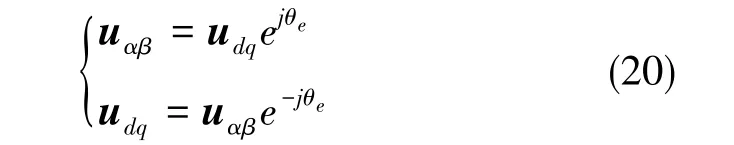
假定在一个完整的开关周期Ts内同步旋转速度ωs保持不变，在t0时刻电流调节器输出电压指令为此时的电压矢量角度为 θe， 则有

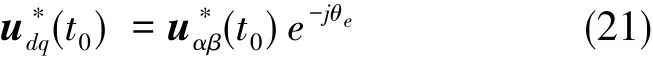
图5为同步旋转坐标系示意图，t0时刻的同步旋转坐标系位置为图5中的红色线。由于采样更新延时，经过Ts／N长的时间后，PWM占空比信号才更新，此时的同步旋转坐标系位置为图5中的蓝色线。在接下来的一个开关周期Ts内，占空比信号转换为实际电压发出。则在[t0+Ts／N，t0+Ts／N+Ts]时间段内，实际作用到同步旋转坐标系的坐标轴上的电压矢量与电压指令之间有如下关系

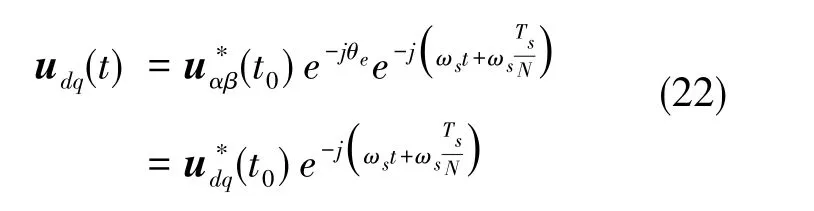
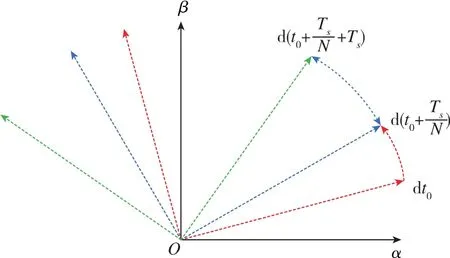
图5 同步旋转坐标系示意图Fig.5 Schematic diagram of synchronous rotation coordinate system

实际作用电压的平均值可以由下式求得[13]

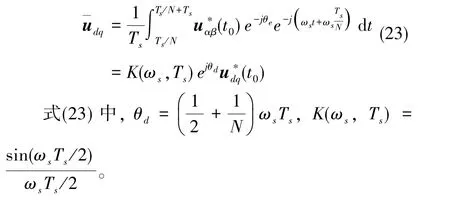
考虑到上述分析，实际作用到负载d轴、q轴上的电压与指令电压满足

4 仿真验证

为了验证上述建立的系统理论模型的正确性，利用Matlab／Simulink建立三相对称阻感负载电流环控制仿真。其中，仿真参数如表1所示。

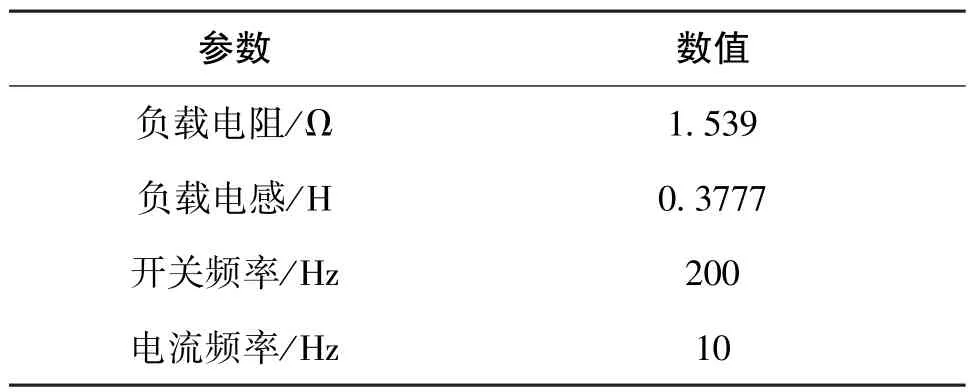
表1 仿真参数设置Table 1 Setting of simulation parameters

0时刻给定d轴电流指令1A、q轴电流指令0A，给定输出采样重数N=2。 比较仿真负载输出电流与理论模型的动态响应过程，可以得到如图6、图7所示的仿真结果。

由图6、图7可知，理论波形与仿真波形基本吻合。图6、图7表明，本文所建立的多采样率状态空间模型是准确的，能够反映实际系统情况。

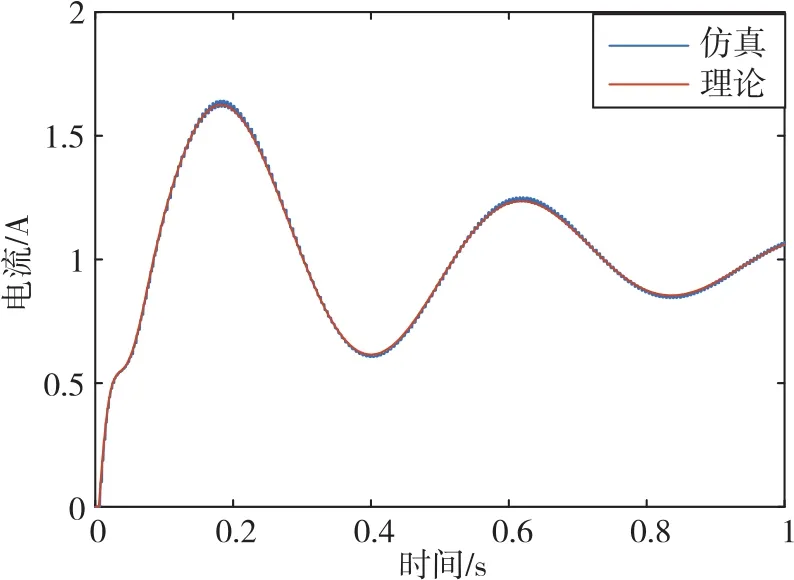
图6 N=2时d轴的电流响应图Fig.6 Diagram of d-axis current response when N=2

图7 N=2时 q轴的电流响应图Fig.7 Diagram of q-axis current response when N=2

5 结论

针对多采样率牵引传动控制中的电流环，本文详细分析了多采样率控制下电流环的结构以及多采样率下电流环数字延时与延时的影响，结合多采样率 “提升”方法，建立了系统电流闭环的等效单采样率状态空间模型。最后，通过Matlab／Simulink仿真验证了本文所建立的数学模型的准确性。仿真结果表明，本文所建立的多采样率控制电流环数学模型是分析多采样率问题的一种有效方法，为进一步分析多采样率系统奠定了基础。