基于深度学习和时频分析的引信干扰信号识别研究

毕明雪，王 旭，白 帆，于承泽，鲁旭东

(沈阳理工大学 装备工程学院，辽宁 沈阳 110159)

0 引言

目前引信工作的电磁环境愈发复杂，干扰信号面临多样性、复杂性等问题，如何准确快速地识别干扰信号变得至关重要。随着计算机智能技术、精确制导技术以及卫星定位技术的发展，国内外引信技术开始向着“引制一体化”和智能化方向发展，从整体上融合导弹态势感知，实现多数据融合分析，智能化起爆控制，实现智能化引信[1，2]。

深度学习是机器学习中对数据进行特征提取学习的新方法。从网络模型来看，并不太关注输入的数据是什么，主要作用在网络特征提取层。传统方法如匹配滤波等方法受限于硬件识别范围有限，而对于深度学习来说，理论上不受硬件识别范围的限制，只受限于发射机的功率限制。因此，深度学习目前广泛应用于计算机视觉、目标检测、跟踪、语义识别等领域[3]，研究人员也尝试将深度学习应用到军事目标识别、导弹自主导航等方面。如文献[4]提出一种基于卷积神经网络对海上舰船SAR图像进行快速识别的方法，通过对网络模型的优化提高了舰船SAR图像的识别速度和准确度。目前已有的做法是基于传统的数学方法，如时频分析方法将时域信号向时频域转换，多用于信号处理方面，如文献[5]基于加窗Wigner-Ville分布的时频峰值滤波对实数域信号进行估计，能够在信噪比-8 dB时恢复信号且估计的信号频率与原始信号接近。目前鲜少有研究人员将深度学习应用到引信干扰信号的识别和抗干扰上来，主要因为深度学习的部署需要一定计算力的硬件平台支撑，而对于引信和弹体结构来说，其结构空间有限，且弹目交会速度极快，需要极高的实时性和准确度。而引信干扰信号作为一维时序信号，各片段具有连续性，相邻信号之间具有相关联系，直接输入到识别网络中可能会损失细节信息，从而导致识别错误。针对以上问题，本文引入条件变分自动编码器网络，考虑将获取的引信回波信号向时频域投影，将一维时序信号识别问题转化为图像特征识别问题。

1 引信回波信号获取及处理

1.1 引信回波模型建立

基于卷积神经网络生成网络模型需要真实且足够数量级的数据集，才能保证网络模型训练的泛化性足够强。由于真实场景下的引信工作环境和数据获取成本较高且较为复杂，因此需要搭建引信回波模型来获取回波信号。由于调频连续波在硬件实现上比较简单，故本文使用调频连续波FMCW(Frequency Modulated Continuous Wave)来获取引信和目标之间的距离等参数，同时采集回波信号获得原始数据集。如图1所示，FMCW的原理[6]是通过计算回波信号和发射信号的差频信号来计算弹目距离和速度。

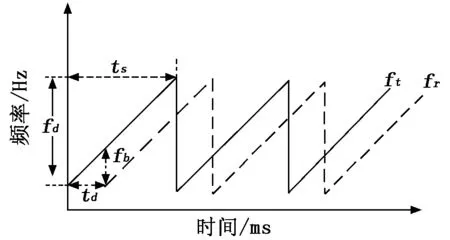
图1 FMCW示意图

图1中，fb为发射信号ft和接收信号fr之间的差频信号，fd为调频扫频波带宽，td为发射信号和接收信号的时间差，ts为扫频周期；设c为光速，弹目距离为D，则有：

fb=fr-ft.

(1)

td=2D/c.

(2)

(3)

在已知其他变量的条件下，则探测距离D可表示为与fb相关：

(4)

搭建引信回波模型可以仿真获取尽可能接近真实工作条件下的回波信号，为后续网络模型训练提供足够多且真实的数据集。

1.2 基于Wigner-Ville分布的时频分析谱图生成

由于获取的引信回波信号是一维时序信号，为了得到回波信号更多的细节信息，本文引入时频分析的方法从而能够同时从时域和频域角度分析信号，其基本思想是：构造时间和频率的联合函数，用它同时描述信号在不同时间和频率的能量密度或强度，简称为时频分布。利用时频分布来分析信号，能给出各个时刻的瞬时频率及其幅值，并且能够进行时频滤波和时变信号研究。常见的时频分析包括短时傅里叶变换、连续小波变换、Wigner-Ville分布和Cohen类分布等[7，8]。

Wigner-Ville分布在时频聚焦性方面表现很好,但易受到交叉项干扰的影响,虽然它的各种平滑改进方法能一定程度上消除交叉项干扰影响,但又会降低时频聚焦性[9]。图2为加噪信号的WVD(Wigner-Ville Distribution)变换得到的时频谱图。

图2 加噪信号的WVD谱图

Wigner-Ville分布可以看成信号s(t)的瞬时自相关函数的傅里叶变换，表示为式(5)：

(5)

(6)

整理后可得：

.

(7)

可以看出WVD在某一频率段内对f进行积分，结果为该信号在t时刻的瞬时能量。同样信号s(t)的傅里叶变换S(Ω)的WVD可表示为式(8),结果为信号在Ω时刻的瞬时能量：

.

(8)

不足之处是WVD面临交叉项干扰的问题，本文引入条件变分自动编码器CVAE(Conditional Variation Automatic Encoder Network)生成网络代替谱图计算过程，采用Wigner-Ville分布对回波信号进行时频变换，经过变换后可以得到回波信号的数学计算真实谱图，为后面的生成网络提供真实的学习方向，采用卷积神经网络代替数学方法的谱图变换可以调用计算机GPU(Graphics Processing Unit)多线程加速计算，以满足干扰信号识别的实时性要求。

1.3 基于条件变分自动编码器的谱图生成网络

CVAE是由变分自动编码器VAE(Variation Automatic Encoder Network)演变而来，而VAE是一种基于概率模型的深度生成网络模型[10，11]。通过编码器将原始数据X转化为隐藏量Z，给定Z的均值和方差且满足正态分布，再通过解码器可以得到近似原数据X的输出X′。

设输入数据X的分布为P(X),其分布未知，而隐含量Z的分布P(Z)是可以给定的，用式(9)来表示P(X)的分布：

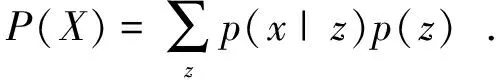
(9)

(10)

考虑通过式(9)、式(10)逆向求解P(X),由于P(Z|X)的概率密度函数p(x|z)无法直接确定，故引入q(z)来逼近p(z|x)，通过KL散度(Kullback-Leibler Divergence)来评价q(z)和p(z|x)之间的相似度，即：

(11)

整理后可得式(12)：

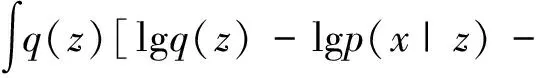
(12)

对于CVAE网络来说，就是引入额外条件约束VAE的生成，如图3所示，在编码器和解码器加入标签y，通过简单卷积层对y进行编码后和x再次输入编码器；为了结果朝着目标生成，同时将编码后的y作为标签输入到解码网络，作为条件约束生成网络的方向，可推导出：

图3 CVAE网络结构示意图

lgp(x|y)=KL(q(z|x,y)||p(z|x,y)+L(x,y)).

(13)

其中：L(x，y)为x、y之间的对应关系函数。

2 模型架构

考虑到目标回波信号的时频特性具有时间上的连续性、特征上的因果性、频谱上的复杂性，单纯对一段时间的时频图像进行特征识别，缺乏对目标/干扰因果特性、目标特征远近关系的识别信息。本文考虑使用CVAE网络生成原始信号的谱图，之后使用卷积神经网络对谱图进行特征提取，最后输入长短期记忆网络(Long Short Term Memory, LSTM)[12,13]，从整体上对干扰类型进行判断。

2.1 整体网络架构

基于深度学习的引信干扰信号识别网络架构如图4所示，以一段处理后的引信回波信号作为原始信号，以一定时间间隔Δt切分原始信号，经过WVD变换得到时频谱图，同时将该段信号输入CVAE网络进行训练，使原始信号在经过CVAE生成网络训练学习后，能够提取出原始信号的谱图，最后将谱图进行特征提取后输入LSTM网络识别。

图4 基于深度学习的引信干扰信号识别网络架构

为了网络模型训练具有更好的真实性，设计了如下两个损失函数约束训练过程，生成谱图后再基于卷积神经网络对谱图中的特征参量进行提取。

2.2 训练过程

在CVAE网络训练过程中，通过KL散度来评价生成数据和真实数据之间的相似度：

KL(q(z|x,y)||p(z|x,y))=lgp(x|y)-L(x,y).

(14)

由图4网络结构中可以看出，经过CVAE训练生成的谱图需要和WVD变换的谱图做均方误差( Mean Square Error， MSE)比较，其中真实值为yi′，训练目标值为yi，则均方误差损失函数可表示为：

(15)

为了防止训练过程陷入局部最优点，引入结构相似性损失函数( Structural Similarity Index， SSIM),类比人的视觉感知，同时考虑了亮度、对比度和结构性指标。假设真实谱图为X，生成的谱图为Y，SSIM计算过程如下：

(1) 首先计算X、Y的均值μX、μY；

(2) 计算图像X、Y的方差和协方差σX、σY和σXY；

(3) 计算中间方程组L(X,Y)、S(X,Y)和C(X,Y)分别表示亮度因子、结构对比因子和对比度因子：

(16)

(17)

(18)

其中：C1、C2、C3为常数。

式(19)即为结构相似性损失函数：

SSIM(X,Y)=L(X,Y)×C(X,Y)×S(X,Y).

(19)

3 实验设计及结果分析

实验分为三部分：第一部分是根据引信回波模型生成原始数据;第二部分是基于CVAE训练生成谱图的过程;第三部分是对生成的谱图进行特征提取，然后经过LSTM识别的结果。

3.1 实验环境

本文训练平台电脑系统为Ubuntu 16.04，显卡为NVIDIA GeForce2070,使用python语言基于Tensorflow架构进行开发调试。

3.2 仿真数据

通过改变干扰数据参数，得到不同回波信号，再经过WVD变换后得到谱图如图5所示，生成的谱图分辨率为128×128。

3.3 基于CVAE生成的谱图

通过CVAE生成的谱图如图6所示，与图5中经过WVD变换的谱图对比，生成效果良好，具备原始数据中的细节信息。

图5 WVD变换后的谱图

图6 基于CVAE生成的谱图

3.4 基于LSTM的干扰信号识别过程

LSTM是一种时间递归神经网络，适合于处理和预测时间序列中延迟相对较长的重要事件。虽然LSTM网络适合对序列数据进行处理，但很难针对序列中的细节进行精确定位及区分，对于单一时间步长内发生的频谱特征缺乏准确定位及细分。因此，拟在LSTM网络的基础上，同时对固定时间步长下的时频谱图进行端到端深度卷积神经网络识别，并将图像的识别特征信息补偿进入LSTM网络，进一步修正网络参数，降低训练过程中梯度消失的风险。

经过CVAE生成的谱图再经过卷积层的特征提取后输入到LSTM进行识别。为了测试网络模型的鲁棒性，设计了消融实验，通过改变卷积层数测试其对识别准确率的影响，经过均值化处理后识别结果如表1所示,其中conv表示卷积层数，dconv表示反卷积层数，FC表示全连接层数，BN表示归一化层数，如2conv+2FC+1BN表示编码器由2层卷积层、2层全连接层、1层归一化层组成。

表1 识别结果

4 结论

本文基于引信回波模型仿真获取目标回波信号，设计了一种基于CVAE的引信干扰信号识别网络，在实验基础上，得到以下结论：

(1) 基于CVAE网络对干扰信号识别可减少由于硬件设备造成的范围受限，能够识别更多干扰类型。

(2) 利用深度学习对回波时序信号进行训练学习可移植到GPU平台进行计算，相比传统时频变换可减少计算量，提高识别速度，为引信工作提供有利条件。

(3) 通过对回波信号测试集进行识别，结果表明该网络对干扰信号具备一定的辨别能力。

同时本文的方法也出现了一些问题，需要对生成网络进一步优化，尝试在简化网络模型的同时对训练数据集中干扰信号的复杂度进行完善，从而更好地模拟真实场景下的干扰信号数据。