基于 的建筑混凝土配合比优化设计研究

陈 艳

（福州软件职业技术学院，福州 350004）

近年来，混凝土作为土木工程（如水利工程、交通运输、房屋建造等）基本的浇筑材料，得到了广泛的关注及迅猛的发展。配置混凝土原材料的种类、性质与使用量等一系列因素直接影响到混凝土的强度、成本和性能，进而关系到土木构造物的造价、品质和寿命〔1〕。因此，明确混凝土的组成材料以及其各成分的用量，使混凝土的性能满足强度性、耐用性和运作性等要求的配合比设计已成为当代混凝土技术的关键环节〔2〕。现有的配合比设计方法主要有5类：传统经验法、解析式法、计算机控制法、专家系统法和人工神经网络等〔3〕。其中，传统经验法的配合比设计方法耗时较长，造成的资源浪费具有不确定性，很难满足当下信息化、高效性、绿色性的工程要求。解析式法需要相应的推算公式与修正方法，而计算机控制法的设计精度并不是很高。专家系统法则存在学习、解释、推理能力差，相关知识获取存在瓶颈，构建系统时间很长等问题。人工神经网络技术大都存在着泛化能力不理想、隐含层节点数不易确定等问题〔4〕。因此，人工神经网络技术还有广泛的研究价值与发展空间。本文通过构建基于海豚算法（dolphin algorithm，DPO）优化BP神经网络模型（DPO-BP），以期得到更好地解决混凝土配合比设计问题的方法。本文先对BP神经网络的权值和阈值进行优化，在确定最优权阈值过程中可以实现对混凝土强度进行预测，并与传统的遗传算法（genetic algorithm，GA）优化BP神经网络（GA-BP）、粒子群算法（particle swarm optimization，PSO）优化BP神经网络（PSO-BP）进行对比，证明了该算法的优越性。

1 方法概述与数据来源

1.1 BP神经网络基本理论BP神经网络一般都具有3层前馈结构，因其在网络训练过程中调整BP网络权值算法的误差函数具有反向传播的特性。在信号向前延伸传播过程中，输入信号的传递路径主线为：输入层—隐含层—输出层。倘若BP网络在输出层得到的预测输出未能达到期望输出的要求，那么网络就会进行反向传播这个负反馈环节。通过不断地修正BP网络的权阈值，使得BP网络预测结果逐渐逼近期望输出。最终，当调整误差小于网络的预设值或达到最大迭代步数时，得到当前BP网络的最优预测输出。BP网络的基本构型见图1。其中，X1，X2，…，Xn为BP神经网络的输入值；Y1，Y2，…，Ym为BP神经网络的输出值；ωij，ωjk为BP神经网络的连接权值。

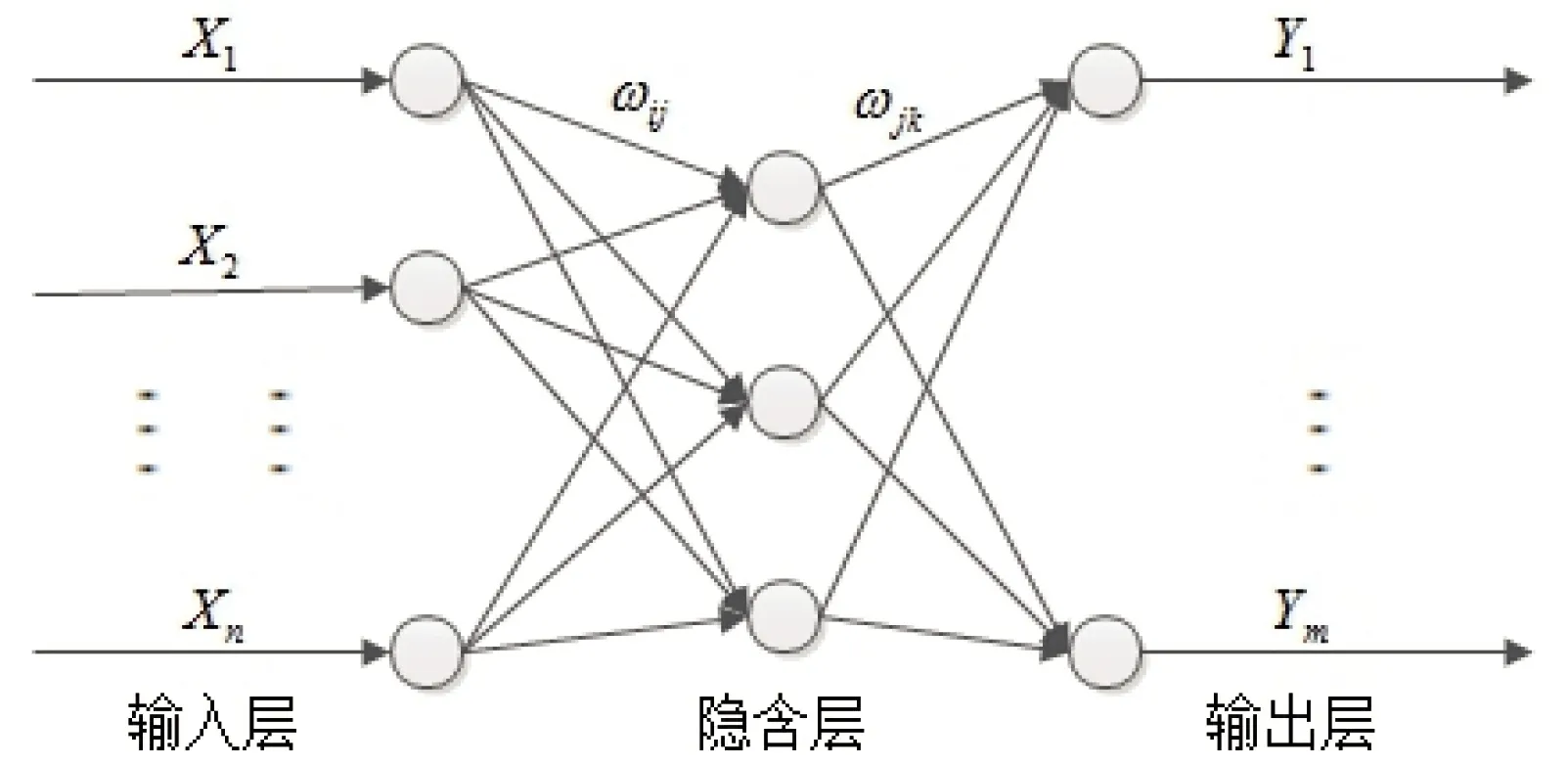
图1 BP神经网络的基本构型

1.2 DPO-BP神经网络的基本理论DPO算法采用海豚觅食过程中从个体到种群的设计方案和分工明确的互助式探索路径的结构,通过海豚个体对自身位置和食物位置的感知和判断、群体间的信息共享，自主进行个体的角色定位，选择首领，以期获得靠近食物的最优位置。将DPO算法与BP神经网络结合，运用DPO算法确定一组BP网络的最优权阈值，可兼具DPO算法的全局寻优及局部细致搜索能力与人工神经网络的映射泛化能力。DPO-BP算法的基本步骤为：

（1）设定DPO参数。初始化海豚群的位置pop=（pop1，pop2，…，popn），海豚种群规模popsize，搜索维数为D，最大迭代次数为Maxgen，海豚个体的伙伴个数为teamsize。其中，维数D用BP网络权阈值总数来表示，即D=m×n+n+n×k+k，m、n、k分别代表输入层、隐含层、输出层的节点数，且按此顺序排列海豚的位置坐标。

（2）构造虚拟团队。为了达到满意的寻优精度，定义以每只海豚popi（i=1，2，…，n）为自己虚拟团队的中心，分别计算海豚popj（j=1，2，…，n）到海豚popi的距离dij。一般情况下海豚个体选择距离相近的m只海豚构建虚拟团队Team，海豚伙伴的距离矩阵采用欧式距离构建。

（3）选取合适的适应度函数。在确定一组最优的BP神经网络的权值、阈值过程中，选择合适的目标（适应度）函数fitnessi也是关键的环节。一般地，选用训练样本构建及训练BP网络，为了检测网络的优劣，通过测试样本对当前训练好的BP网络进行误差检测，由sim函数可以得到网络的预测输出O=（o1，o2，…，on）；若将测试样本期望输出记为Y=（y1，y2，…，yn）；把预测输出和期望输出之差的均方误差值作为个体适应度值F，计算公式为：

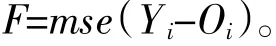
（4）确定海豚群最优位置。根据各海豚团队中海豚个体的BP预测仿真值，由适应度函数公式确定每个团队的最优解fxbesti（i=1，2，…，n）和最优位置pti（i=1，2，…，n），以及海豚群的最优解fxbest和最优位置pni。

（5）更新海豚位置。作为团队的普通成员，海豚个体的位置更新公式。

（6）若迭代寻优次数达到Maxgen，则网络训练结束，得出海豚群最优位置（即一组最优权阈值），否则跳转步骤（2）。

（7）用此权值和阈值构建BP用于接下来的样本评价。

1.3 数据来源与处理工程上一般选取混凝土28 d抗压强度作为评价混凝土质量好坏的重要指标之一，本文即选用该指标作为混凝土抗压强度预测及配合比设计的唯一评价指标。以文献〔5〕的样本数据为研究对象，影响混凝土28 d抗压强度的因素包括炉石、超增塑剂、水泥、粉煤灰、水、碎石与沙用量等7种〔5〕，样本数量共选取90组。本文选取前80组数据作为BP网络的训练样本，后10组数据作为BP网络的测试样本。BP神经网络结构选取为3层，输入层的节点数为5，隐含层的节点数选取为10，输出层的节点数为1。设定海豚群的整体大小为N=20，海豚个体的维数D=71，海豚群伙伴个数teamsize=5，最大迭代次数Maxgen=50。由于这90组数据中诸多影响因子之间单位不统一，数量级相差许多，且数据大的话需要的神经网络神经元也较多，可以选择数理统计里惯用的归一化处理方法。另外，把测试样本的测试误差的均方误差和R2值当作衡量一个网络泛化能力的标准。

2 结果分析

2.1 DPO-BP预测混凝土强度结果混凝土强度预测中，DPO-BP算法与BP神经网络的对比图见图2。从图2中可以看出，DPO-BP算法预测结果明显优于BP神经网络的预测结果。另外，从数据上可以分析出，在混凝土强度的预测中DPO-BP算法的均方误差为0.000 3，远远小于BP神经网络的均方误差0.027 1。此外，DPO-BP算法的R2=0.997 7较BP神经网络的R2值更接近于1。

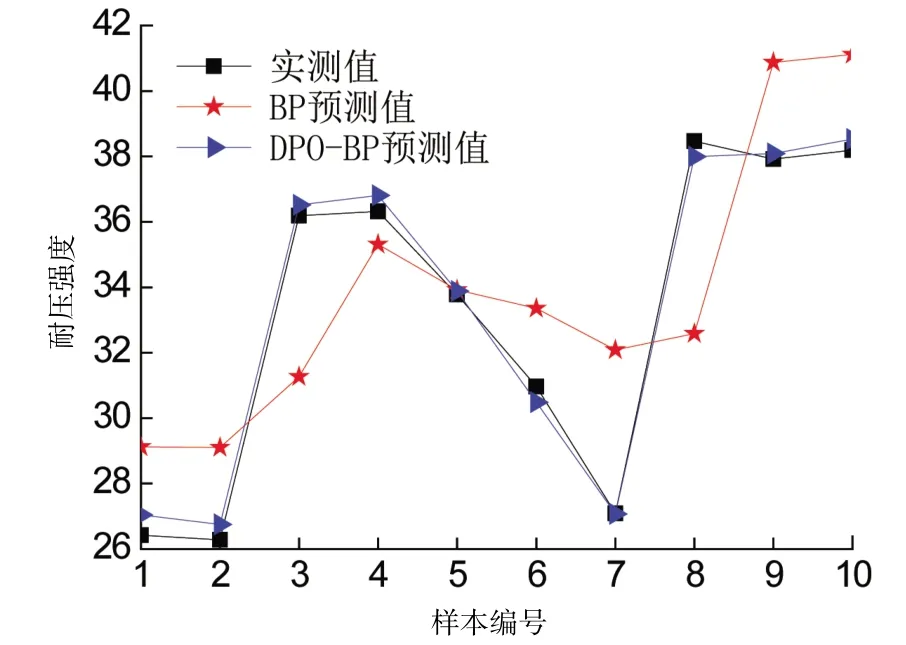
图2 测试样本对比图

2.2 DPO-BP预测混凝土强度的优越性为了判断及证明DPO-BP算法预测模型的优越性，将文献〔6-7〕中采用的PSO与GA分别与BP神经网络的算法结合并相对比，结果见图3。由图3可以得出，除了第2个样本的预测结果与真实混凝土强度相差0.69之外，DPO-BP较其他两种算法预测效果更好。

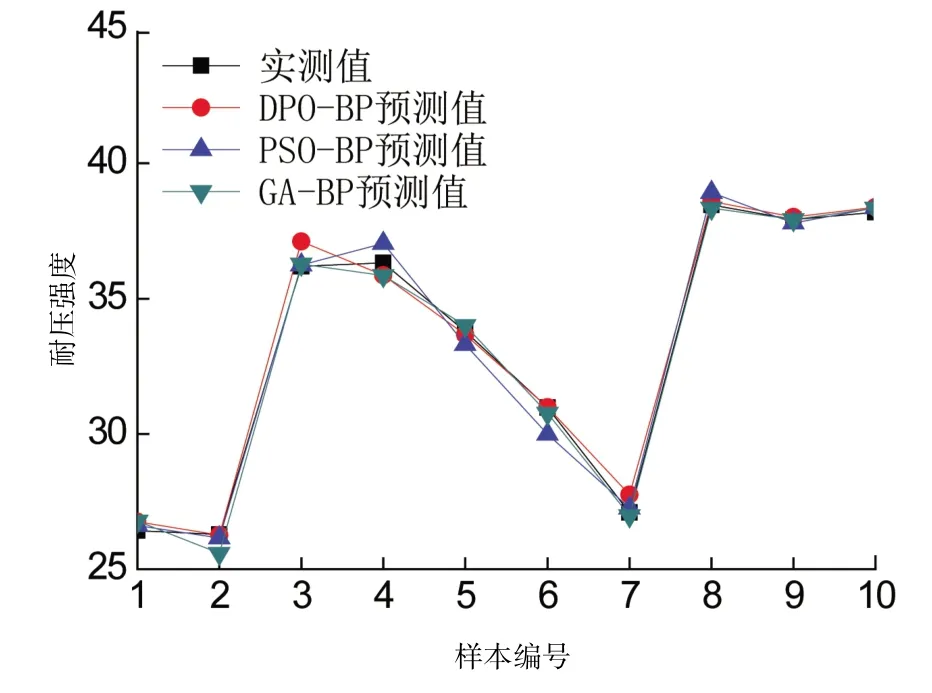
图3 不同算法的预测结果对比

3种启发式算法优化BP神经网络的性能见表1。在Maxgen的条件下，DPO-BP算法与其他两种算法误差相比，前者的收敛速度较快、精度较高；GABP神经网络的收敛速度与精度次之；PSO-BP算法的精度在三者中最低。其中DPO-BP算法的仿真误差最小，为0.033 5%，R2=0.998 7较其他两者更接近于1。但是在算法运行时间上，GA-BP神经网络的运行时间最短为206.67 s，DPO-BP算法的程序运行时间次之，PSO-BP算法的运行时间最长。

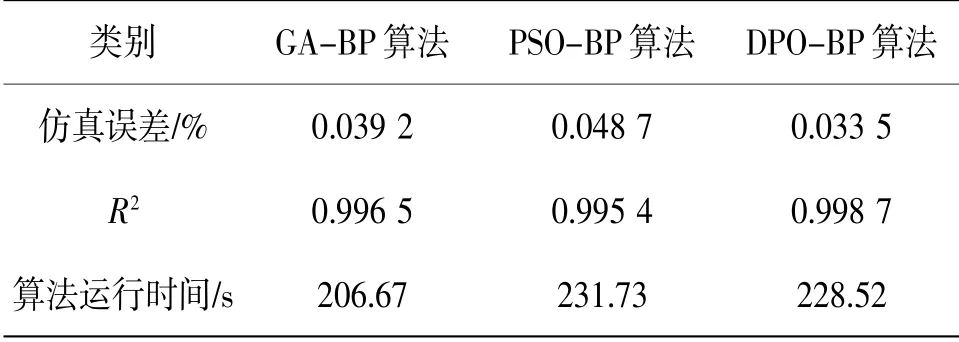
表1 不同算法的性能对比

2.3 混凝土算例验证为了验证该DPO-BP算法设计配合比的可行性和准确性，以一个算例进行测试。例如，选取混凝土期望强度DesiredValue=39。通过DPO-BP算法，得出最佳的配合比为水泥、粉煤灰、水、碎石、砂用量分别为243.351、260.013、193.548、884.919，901.617 kg/m3。该配合比下的适应度值为F=3.126×10-13，误差较小，再与给出的样本数据相比较，契合度较高。算法的误差变化曲线见图4。

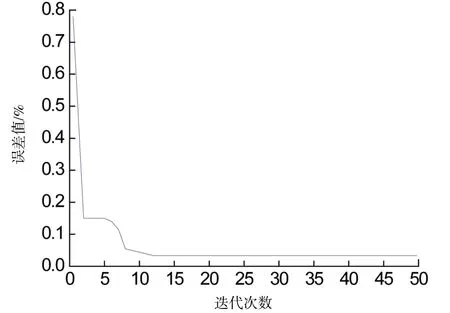
图4 DPO-BP算法误差变化曲线

3 结论

本文将DPO算法用于BP神经网络的优化，由于DPO算法具有较高的收敛速度、寻优精度，将DPO-BP用于混凝土的强度预测与配合比设计上，并与BP、PSO-BP、GA-BP等算法进行对比分析。结果显示DPO-BP的寻优精度较其他算法更高，收敛速度也更快，预测、配合比设计效果较好，泛化能力较强。为了找出混凝土强度的主要影响因素，本文在分析过程中，使用了归一化、主成分分析等方法，明确了影响混凝土质量的主要因素，与其他文献的混凝土强度影响参数进行了对比，发现找出的主要参数可信度很高。DPO-BP算法求解精度高、可移植性强，还可以用作边坡稳定性判断、机器故障诊断、空气水体质量评价等诸多领域，具有重要的工程价值。