长江口台风期间波致增水空间分布特征研究

王雪迎，潘毅，张壮，于普兵，陈永平

（1.河海大学海岸灾害及防护教育部重点实验室，江苏南京210098；2.河海大学港口、海岸与近海工程学院，江苏南京210098；3.浙江水利科学研究院，浙江杭州310020）

1 引言

风暴潮是世界上摧毁力最强的海洋灾害之一，产生的增水和巨浪严重威胁沿海区域人们的生命财产安全。长江口沿岸区域人口密集，经济繁荣，是中国的经济中心之一，但其常受台风引起的风暴潮和巨浪的影响。风暴潮潮位受到众多因素影响，如径流、台风、波浪和天文潮等。此外，长江口地形复杂，三级分汊四口入海，且分布着许多水下浅滩（见图1），这使得潮（天文潮和风暴潮）和波浪间的相对作用更加复杂，对这种相互关系量级和空间分布的理解对于风暴潮期间长江口沿岸海域的海岸洪水预警预报有重要意义。潮汐和风暴潮都会对波浪产生显著影响，这种影响的主要控制因素为潮位；波浪通过辐射应力对潮流和潮位产生影响，影响程度受到岸线地形等诸多因素的控制，需要针对具体区域进行研究。

图1 长江口地形

风暴潮波致增水研究始于20世纪80年代[1]。波浪主要通过改变表面应力和底部应力对潮位产生影响，同时，波浪辐射应力对近岸区域也有显著影响。考虑潮波相互作用的模型已广泛应用于风暴潮数值计算中[2]。学者对不同区域的波致增水特征开展研究。针对中国东南沿海地区风暴潮的分析指出，波浪在近岸形成增水，离岸形成减水[3]，增水分布还受到风场、风生流和岸线特征的共同影响[4]；辐射应力对风暴潮过程中的水位上升有2%～5%的贡献[5-6]。研究表明，渤海沿岸的增水过程是由局地风“直接作用”及外部天气系统“间接影响”的共同作用引起的[7]，渤海湾海域波致增水最大可达0.3 m[8]，波致减水也能到达0.2～0.3 m[9]。中国东海的波致增水研究表明，风暴潮期间长江口的波致增水比中国沿海的大多数地区更为明显，波致增水高达0.3 m[10]，其中，针对1109号台风“梅花”的研究表明，长江口近岸破波带的波致增水总体在0.1～0.18 m[11]。目前，大多数针对长江口波致增水的研究仅基于单一台风，导致研究成果的代表性不强；另一方面，关于长江口的波致增水结论通常仅给出量级上的范围，缺乏对其的空间分析。本研究通过数值模拟的方法，模拟了7场影响长江口区域不同特征的典型台风过程，分析了长江口区域台风期间的波致增水的量级和空间分布特征，给出了定量的结论，为长江口沿岸的防洪减灾预警预报工作提供参考。

2 数值模型的建立

本研究基于近岸海洋数值模式ADCIRC（an ADvanced CIRCulation model for oceanic，coastal and estuarine waters）[12]和第三代海浪模式SWAN（Simulating WAves Nearshore）[13]模型建立风暴潮-台风浪耦合模型，比较耦合模型与非耦合模型的计算结果，得到长江口台风期间波浪对水位的影响。

ADCIRC模型是北卡罗来纳大学等多所大学联合开发的有限元海洋模型，在沿海水动力模拟中有众多成功的应用[14]。其控制方程是由动量方程与通用波动连续性方程（Generalized Wave Continuity Equation，GWCE）组成的二维浅水方程。动量方程的形式为：

式中，U、V分别为x、y方向上的垂向平均分量；H为总水深；f为科氏力系数；pξ为自由表面大气压；ρ0为水密度；g为重力加速度；η+γ为牛顿潮势和地球潮等作用；τξx和τξy为表面切应力，τbx和τby为底部摩擦力；Dx和Dy为扩散项，Bx和By为斜压 梯 度项。GWCE方程是通过对原始连续性方程对时间求导得到的，重新排列空间和时间导数，将其中流速的时间导数项用动量方程消去，再将原始连续性方程乘上一个权重系数的乘积，最后得到下式：

式中，ξ为自由水面高度。

SWAN模型是代尔夫特理工大学（TU Delft）基于波作用量守恒方程开发的第三代波浪模型，被广泛应用于风浪模拟[15]。SWAN模型的控制方程为波作用密度平衡方程，方程形式为：

式中，N为波作用密度；t为时间为地理空间坐标向量为波群速向量为环境流速向量；cg与cθ分别为波作用密度在谱空间内的传播速度；Stot为源汇项。式（3）左侧第一项表示波作用密度在时间尺度上的变化，第二项为二维地理空间中波能量的传播，第三项表示由于水深和环境流的变化导致的频率偏移的影响，第四项表示由于水深和环境流引起的折射；式（3）右侧是包含了能量的输入与耗散过程的源汇项，主要包括风能输入，白浪、底部摩擦和波浪破碎引起的能量耗散以及波浪的三阶、四阶非线性相互作用引起的波能交换。

模型中的风场使用Holland模型[16]进行计算。在指数型气压分布模型的基础上，针对不同台风径向气压变化速率的区别，引入了形状系数B，气压场计算公式如下：

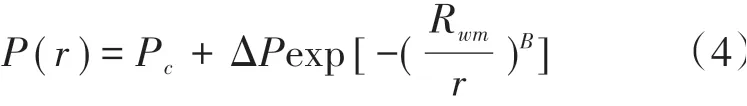
式中，P(r)是半径r处的气压，Pc是台风中心气压，ΔP是风场最外围气压与台风中心其他的差值；Rwm是最大风速半径，由Knaff提出的经验公式确定：

式中，Vmax为最大风速（此处单位为节）；ϕ为当前纬度。

参数B由以下公式确定：

式中，Vmax为最大风速（单位为m/s）；Vt为台风移动速度；Wrdc为折减系数，默认取0.9；Vr为计算风速；ρa为空气密度；e为自然对数。

模型使用了两层嵌套的计算网格系统。一级网格覆盖了东中国海的大部分区域，为二级网格提供边界条件。二级网格从长江口外延伸至大通站。一级网格的计算节点和网格单元数分别为22 779和43 549，二级网格的计算节点和网格单元数分别为44 241和81 100（见图2）。一级网格的外海边界条件由TPXO 7.2海潮模型提供，二级网格的外海边界由一级网格提供，上游流量边界采用大通站的实测流量数据。

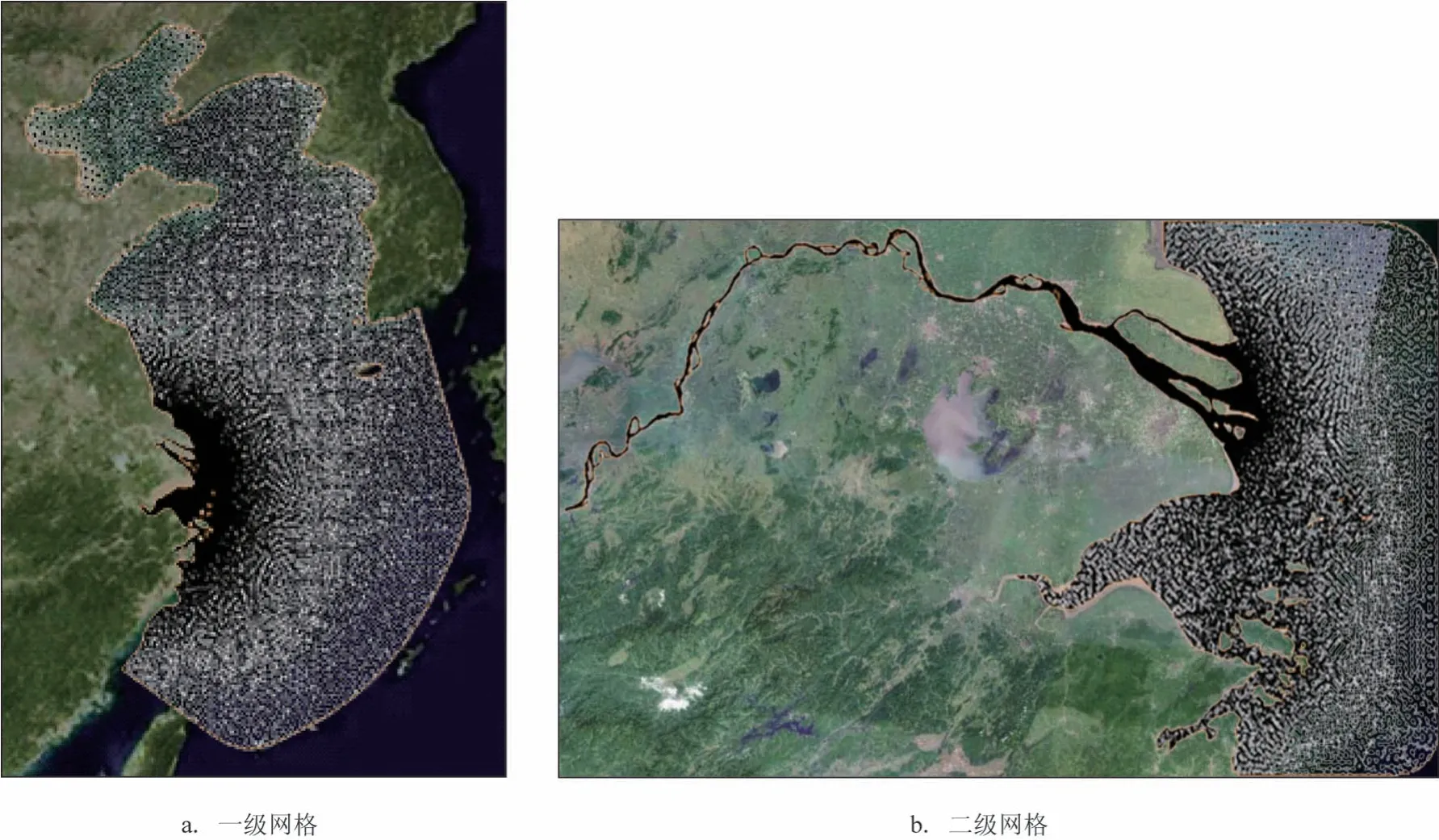
图2 计算区域和网格

3 模拟方案与模型验证

选取近年来影响长江口7场不同特征的典型台风过程进行模拟，分别为：0807号台风“海鸥”、0908号台风“莫拉克”、1109号台风“梅花”、1416号台风“凤凰”、1509号台风“灿鸿”、1810号台风“安比”和1812号台风“云雀”。通过比较杨林站的模型计算结果和实测潮位来验证该模型，对比结果显示（见图3），模型计算结果与实测结果整体上吻合良好。

图3 不同台风过程的风暴潮验证（杨林站）

使用耦合模式模拟0509号台风“麦莎”与1210号台风“达维”过程。将模型计算波高与南槽东站（122.25°E，31.14°N）和响水站（120.10°E，34.44°N）两处的实测波高数据进行对比，验证波浪计算结果。对比结果表明（见图4），模型能够较好地捕捉台风引起的波浪过程。

4 模拟结果分析与讨论

在耦合模式与非耦合模式下分别模拟风暴潮过程，其中非耦合模式即采用单一的潮流模型进行计算，两种模式均考虑风拖曳力、气压作用和上游径流等物理过程，不同的是耦合模式采用SWAN模型计算波浪场，并通过交换流速、水位和辐射应力等因素，实现潮和浪的双向耦合。由耦合模式和非耦合模式分别计算得到考虑与不考虑波浪情况下的潮位分布，二者相减得到风暴潮过程中的波致增水空间分布。图5给出了每个台风过程中波致增水的最大值，结果表明，不同场次台风的波致增水有明显的不同。波致增水最大值的总体分布特征有明显规律，最大波致增水主要集中在崇明岛东部和九段沙周围的浅滩。在南支的北岸和北支的上游，波致增水十分明显；而在徐六泾上游的河道中，波致增水微乎其微。

图5 各场台风过程中波致增水最大值（单位：m）

为了估算风暴潮期间长江口波致增水最大值的空间分布，在图5基础上，对所有模拟台风场次的波致增水取最大值（见图6）。如图6所示，台风期间波致增水的最大值超过15 cm，主要分布于崇明岛东部和九段沙周围的浅滩，徐六泾到长江口河道的浅滩处也可能发生5～10 cm的波致增水，徐六泾上游河道观察到的波致增水低于5 cm。

图6 所有台风过程中的最大波致增水（单位:m）

根据波致增水的分布特征和长江口的地形，选择17个观测点对台风期间的波致增水变化进行分析（见图7）。根据地理位置将观测点分为4类，即口外浅滩、南支、北支和上游河段（见表1）。对不同区域的台风过程中观测点处的波致增水特征进行分析（见图8），图8a中蓝色条柱代表各场台风中最大波致增水平均值，工字线段表示各场台风中最大波致增水变化范围；图8b中分别使用红、黄、蓝3根立柱在地图相应位置上标出不同台风中最大波致增水的最大值、平均值与最小值。如图所示，从河口到上游河段，从浅水到深水，波致增水的幅度呈下降趋势。口外浅滩波致增水最大，其次是南支和北支，上游河段最小。除九段沙尾部的浅滩（p7）外，浅水区其他观测点的波致增水的最大值范围为0.05～0.1 m，而深水和徐六泾上游河段总体小于0.05 m。总体而言，九段沙、崇明岛东侧及南支北岸的波致增水十分明显，而徐六泾上游的河道中无明显波致增水，由此得出，波致增水的空间分布主要受地形及水深控制。在浅滩处，波致增水较大，而在水深较大处，波致增水较小。波致增水的空间分布也与波生流有关，以1509号台风为例，将波生流矢量图与地形云图叠加绘制于图8。如图9所示，启东沿岸、崇明岛东部沿岸、九段沙沿岸及浦东沿岸等波致增水显著区域均存在明显流向口内的沿岸流。分析认为，水体由口内流向口外过程中，受波生流影响，在口门沿岸至口外流速降低，水体堆积，从而产生显著波致增水。

图7 波致增水观测点

表1 观测点分类

图8 观测点波致增水的范围

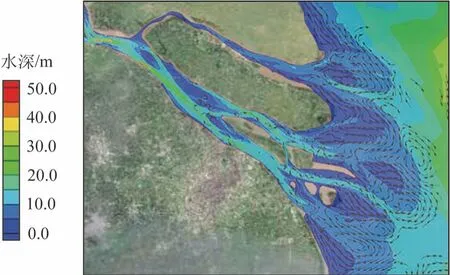
图9 1509号台风波生流与地形叠加图

在耦合模式下输出各场台风过程中的有效波高，取其最大值，绘出长江口台风期间最大有效波高分布。从图10可以看出，长江口口门内最大波高在3 m以内，北支和南支九段沙以内最大波高不超过2 m。由于波高衰减时与潮流发生强烈能量交换，引起了较强的波浪作用，因此，波高衰减较快的位置也是波致增水最大的位置。

事实上，由于不同特征台风在不同位置造成的增水特征有所不同，所以在河口海岸防灾减灾或实时预警中，波致增水的最大值更有意义。波致增水最大值彰显了一次台风过程中，波浪对潮位的影响可能到达的量级。由图10可知，南支内测点波致增水的最大值大约在0.04～0.08 m，而长江口南支的潮位在相关区域防灾减灾中是重要的参考依据，因此在实际防灾减灾或预警预报中，可以根据预报模型本身的精度，以及波浪计算的代价来具体分析是否考虑波浪作用。口外浅滩测点波致增水的最大值可达0.18 m，因此，当涉及计算浅滩处风暴潮期间水位过程时，最好考虑波浪因素的影响。

图10 所有台风过程中的最大波高分布

为了分析波致增水和台风强度的关系，将各测点的最大波致增水、台风最低中心气压关系、最大波致增水和台风最大风速的关系绘于图11。如图所示，波致最大增水与台风中心气压负相关，与最大风速正相关，即在更强的台风过程中，波浪也会引起更大的额外增水。

图11 最大波致增水与台风强度的关系

大部分台风过程都以波致增水为主，当波致增水较明显时，增水主要分布在口外浅滩。除此以外，距离口外浅滩较远处会产生一定波致减水，其量级通常小于近岸的波致增水，对于防灾减灾的预警工作影响不大，因此，本文不再作进一步讨论。

5 结论

建立了基于ADCIRC-SWAN模型的风暴潮与台风浪耦合模型，研究长江口在台风过程中的波致增水特征。对近年来影响长江口的7个台风风暴潮过程进行了模拟，通过对模拟结果的分析探讨了长江口的波致增水特性。

总体来讲，长江口海域波致增水的量级大致在0.05～0.15 m之间。从空间分布的角度来看，口外浅滩的波致增水最大，可达0.15 m以上；南支和北支次之，其值总体在0.05～0.1 m；上游河段的波致增水相对最小，大致不超过0.05 m。综合2008—2018年10 a间显著影响长江口7场台风风暴潮模拟结果，最大波致增水主要集中在崇明岛东部和九段沙周围的浅滩。在南支的北岸和北支的上游，波致增水十分明显，而在徐六泾上游的河道中，波致增水微乎其微。同时，南支内测点波致增水的最大值大约在0.04～0.08 m，而口外浅滩测点波致增水的最大值可达0.18 m。长江口波致增水空间分布特征可直接为长江口沿岸的防洪减灾和预警预报工作提供参考依据。

根据本文得到的长江口波致增水空间分布特征，南支的最大波致增水通常在0.1 m以下，因此在防灾减灾预警预报中，可以根据预报模型本身的精度，以及波浪计算的代价来具体分析是否考虑波浪作用；另一方面，口外浅滩测点波致增水的最大值可达0.18 m，因此，当涉及浅滩处风暴潮期间水位数值计算时，则需考虑波浪因素的影响。