若干新型智能优化算法对比分析研究

张九龙，王晓峰，芦 磊，牛鹏飞

1.北方民族大学 计算机科学与工程学院，银川750021

2.北方民族大学 图像图形智能处理国家民委重点实验室，银川750021

用于解决优化问题的方法叫作优化算法，它是基于某种思想或机制，通过一定的途径或规则得到满足问题要求的解的过程。传统的优化算法如遗传算法、蚁群算法、粒子群算法、模拟退火算法、禁忌搜索算法等，这类算法构造直观，原理便于理解，通常被称作智能优化算法（intelligent optimization algorithms，IOA）或现代启发式算法（meta-heuristic algorithms，MA）。按照算法原理的不同，智能优化算法可以分为以下几个大的类别：仿人智能类算法、进化类算法、群体智能类算法、仿植物生长类算法、仿自然类算法等。

仿人智能类算法是指一类包括模拟人脑思维、人体系统、组织、器官乃至细胞及人类社会竞争进化相关的算法，其中经典的算法有神经网络算法、免疫算法、禁忌搜索算法、头脑风暴算法、帝国主义竞争算法等。进化类算法是一类模仿自然界的生物在生殖繁育过程里，通过遗传和变异及“优胜劣汰”自然选择法则不断进化的算法，在一些可行解组成的种群中，迭代进化寻求最优解。主要算法包括遗传算法、差分进化算法、基因表达式编程算法等。群体智能类算法是从自然界群居生物的觅食、繁殖等行为或群体捕猎及生存策略中获得灵感，设计模型对问题求解的优化算法，核心思想就是若干个简单的个体构成一个群体，通过合作、竞争、交互与学习等机制实现高级和复杂的功能，在缺少局部信息和模型的情况下，仍能完成复杂问题的求解。其中代表性的算法有蚁群优化算法、粒子群优化算法、人工蜂群算法、布谷鸟搜索算法等。仿植物生长类算法指的是模拟花草树木等植物在生长过程中表现出来的向光性、根的吸水性、种子繁殖、花朵授粉等特性而构造出的优化算法，主要算法有入侵杂草优化算法、森林优化算法、花朵授粉算法等。仿自然类优化算法是指模拟风雨云电等自然现象或物理、化学、数学定律等非线性科学的优化方法，其中较知名的算法有模拟退火算法、闪电搜索算法、引力搜索算法、热传递搜索算法等。

随着人工智能及工业技术的发展，对算法性能的要求越来越严格，然而一个算法在某些优化问题上表现出来的优异性能并不代表同样适用于其他类型的优化问题，因此近年来不断有新型智能优化算法提出，用于解决不同类型的优化问题。相较于传统的智能优化算法，新型智能优化算法在收敛速度、求解时间、计算精度等不同方面各有侧重，为解决优化问题提供了新的思路和方法。本文按照算法提出的时间选取了2015 年以来的若干新型智能优化算法，分别是2015 年提出的蝴蝶优化算法、飞蛾扑火优化算法，2016 年提出的正弦余弦优化算法，2017 年提出的蝗虫优化算法，2019 年提出的哈里斯鹰优化算法和2020 年提出的麻雀搜索算法，本文详细介绍了各算法的基本原理、算法流程和相关改进策略，并从求解的平均值、标准差、最优值、最差值、平均运行时间及收敛曲线6 个指标对算法性能对比分析，最后是对智能优化算法未来研究发展的展望。

1 相关算法描述

1.1 蝴蝶优化算法

Arora 等在2015 年提出一种新的元启发式智能优化算法——蝴蝶优化算法（butterfly optimization algorithm，BOA），蝴蝶优化算法所涉及的主要公式如下：

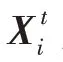
蝴蝶优化算法的大致流程为：蝴蝶在迭代过程中产生一定的香味，依据香味浓度指导蝴蝶在搜索空间内移动，每次迭代生成一个随机数与转换概率进行比较来决定全局搜索或局部开发，循环迭代直至满足终止条件算法结束。

蝴蝶优化算法原理简单，便于理解，但和其他智能优化算法一样，也存在容易陷入局部最优、收敛性差的问题。为此不断有新的改进蝴蝶优化算法被提出来，选取了部分改进的相关文献并从改进策略、优势、局限和应用场景等方面归纳如表1 所示。

除表1 中列举出的各种改进方法外，还有其他的一些改进和应用，如文献[34]中，采用了可变感知模态参数策略，以提高蝴蝶优化算法的收敛速度。文献[35]在BOA 中嵌入了学习自动机，利用学习自动机配置蝴蝶的行为，在全局搜索和局部开发之间建立适当的平衡。宁杰琼等提出混合策略改进的蝴蝶优化算法，采用Circle 映射初始化蝴蝶个体的位置，通过动态切换概率控制正弦余弦算法与蝴蝶优化算法的转换，将自适应余切权重系数引入位置更新中，并添加逐维辨析策略避免算法陷入局部最优。Rachapudi 等将蝴蝶优化算法用于染色图像中细胞核的分割；李鹏等将改进蝴蝶优化算法和例子滤波的联合算法用于锂电池健康状态预测。

表1 蝴蝶优化算法改进分析Table 1 Improvement analysis of BOA

1.2 飞蛾扑火算法

飞蛾扑火算法（moth-flame optimization，MFO）是在2015 提出的一种群智能优化算法，该算法的灵感来源于自然界中飞蛾的横向定位（transverse orientation）导航机制，以对数螺线形式更新位置的飞蛾扑火算法涉及到的主要公式有：

其中，M表示第只飞蛾；为螺旋形函数；F表示第个火焰；D表示第只飞蛾与第个火焰之间的距离；参数称为极半径，是定义对数螺旋形状的常数；称为收敛常数，是[-1,1]之间的随机数，用于定义飞蛾下一个位置距离火焰的程度；为火焰数量；是火焰最大数量；为当前迭代次数；是最大迭代次数。

飞蛾扑火算法的大致流程为：初始化飞蛾种群，计算每只飞蛾的适应度值并选择其中前个作为火焰。每次迭代均计算火焰和飞蛾的适应度值进行排序并更新角色。火焰数随着迭代次数的增加而减少，一直迭代直到满足终止条件算法结束。

飞蛾扑火算法的改进有很多，选取了部分改进的相关文献并从改进策略、优势、局限和应用场景等方面归纳如表2 所示。

除表2 中列举出的各种改进方法外，还有其他的一些改进和应用，如王光等在算法中引入历史最优火焰平均值的概念，改进飞蛾位置更新公式，使用随机反向学习策略进行反向学习，引入折射原理对解进行折射操作。刘小龙在飞蛾扑火算法中引入缩放因子和视距因子的概念，在协同演化框架下，提出飞蛾直飞模型，使得算法解决大规模优化问题表现出较好的优越性和鲁棒性。文献[49]中定义了全局搜索和局部开发之间的混合阶段，增加依赖适应度的权重因子来更新飞蛾的位置。文献[50]将MFO 算法应用于混合无线宽带接入网领域，提出一种新的基于自然启发的多光纤网络单元布局启发式飞蛾扑火算法。文献[51]中提出将飞蛾扑火算法和频域法相结合，用于永磁同步电机控制器参数整定，提高了系统的快速跟踪能力和抗干扰能力。

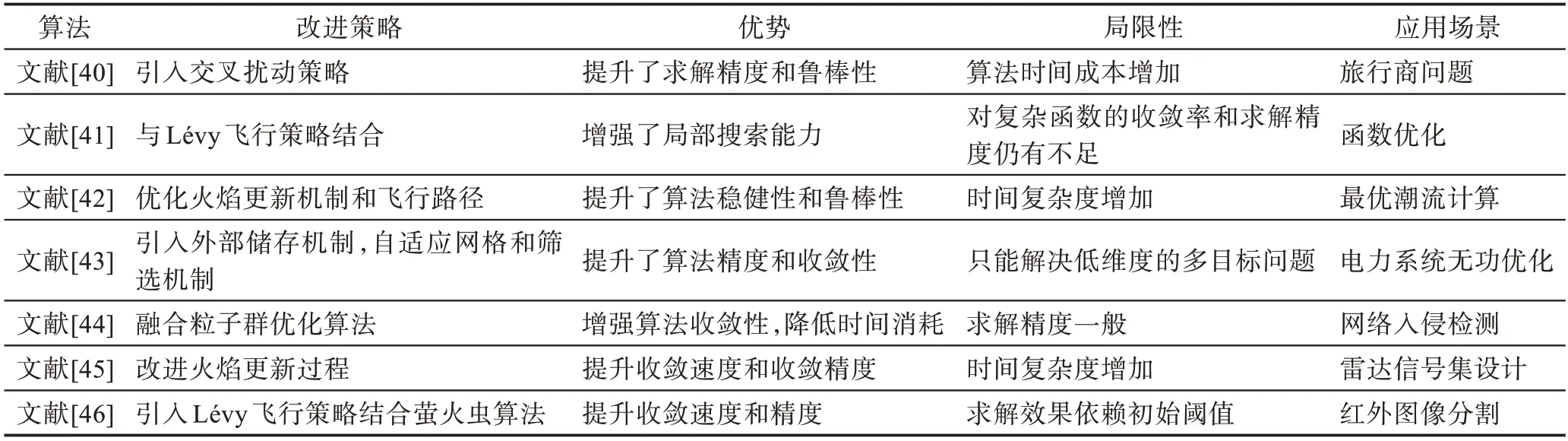
表2 飞蛾扑火算法改进分析Table 2 Improvement analysis of MFO

1.3 正弦余弦优化算法

正弦余弦优化算法（sine cosine algorithm，SCA）是Mirjalili 教授2016 年提出的新型智能优化算法，正弦余弦优化算法所涉及的主要公式有：

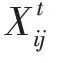
正弦余弦优化算法的大致流程为：初始化种群，计算种群中个体的适应度值，更新参数、、、并根据式（7）不断更新个体的位置，更新种群最优个体，持续迭代直至满足终止条件算法停止。

很多学者对正弦余弦优化算法的改进不断探索，选取了部分改进的相关文献并从改进策略、优势、局限和应用场景等方面归纳如表3 所示。

表3 正弦余弦优化算法改进分析Table 3 Improvement analysis of SCA

除表3 中列举出的各种改进方法外，还有其他的一些改进和应用，如文献[60]提出基于改进正弦余弦算法的极限学习机（modified sine cosine algorithmextreme learning machine，MSCA-ELM）并在脑部病理核磁共振图像分类中得到了应用。于坤等将改进的正弦余弦算法与多种光谱线型拟合方法相结合，用于计算对应的光谱特征峰位置。文献[62]将正弦余弦算法和遗传算法混合用于数据挖掘中的特征选择，取得了较好的效果。

1.4 蝗虫优化算法

蝗虫优化算法（grasshopper optimization algorithm，GOA）是Saremi 等在2017 年提出的一种模仿自然界中蝗虫迁徙及觅食的元启发式智能优化算法。蝗虫优化算法的主要公式如下：

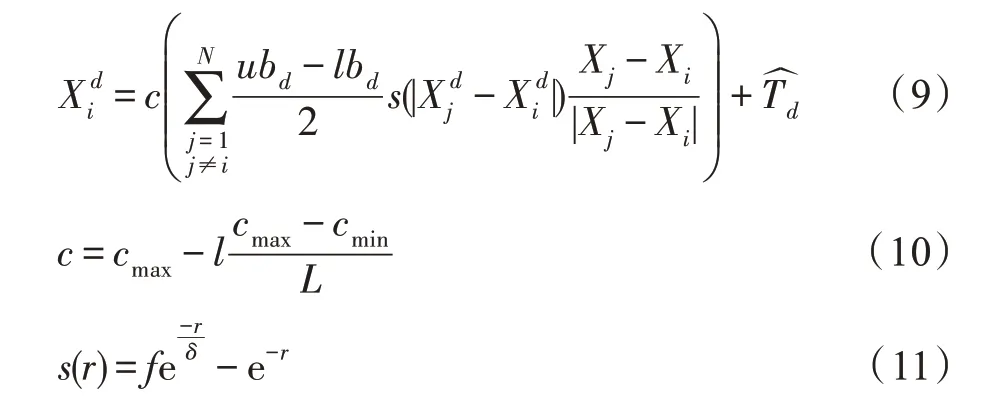
蝗虫优化算法的大致流程为：初始化种群位置及参数，通过式（9）及式（10）循环更新参数和蝗虫位置并计算每个蝗虫的适应度值，每次迭代保存种群中最好适应度值的个体，持续迭代并判断迭代次数是否达到设定的最大值。若未达到最大迭代次数继续迭代，否则退出循环并返回全局最优解。

蝗虫优化算法与其他群智能优化算法一样，存在一定缺陷。不断有学者及研究人员对其进行改进，选取了若干改进的方法归纳如表4 所示。

除表4 中列举出的各种改进方法外，还有其他的一些改进和应用，如王博等在此基础上进一步提出混合多目标蝗虫优化算法，利用Halton 序列进行种群初始化，由差分变异算子引导种群更新并加入自适应权重因子，提高了算法优化效率和解集质量。文献[72]提出基于反向学习策略改进的蝗虫优化算法，第一阶段使用反向学习策略生成初始种群，第二阶段使用反向学习作为附加阶段在每次迭代中更新蝗虫种群，通过基准函数及工程问题验证了算法有较好的性能。Arora 等将混沌理论引入GOA 的优化过程中利用混沌映射在局部开发和全局搜索间做到有效平衡。文献[74]将蝗虫优化算法用于数据聚类。潘峰等使用蝗虫算法进行寻优求解最佳阈值，并利用最佳阈值对图像进行分割等。

表4 蝗虫优化算法改进分析Table 4 Improvement analysis of GOA

1.5 哈里斯鹰优化算法

哈里斯鹰优化算法（Harris hawks optimization，HHO）是Heidari 等在2019 年提出的一种新型群智能优化算法，哈里斯鹰优化算法主要包括探索阶段和开发阶段。

探索阶段的主要公式为：

式中，为当前种群中随机选择的个体；为当前最优个体；X为种群个体的平均位置；、、、均为0 到1 之间的随机数；和分别为种群的上下边界；为种群数量。

探索阶段到开发阶段的转换公式为：

式中，代表控制算法全局搜索和局部开发的逃逸能量因子；是-1 到1 的随机数；为当前迭代次数；为最大迭代次数。

开发阶段软包围公式有：

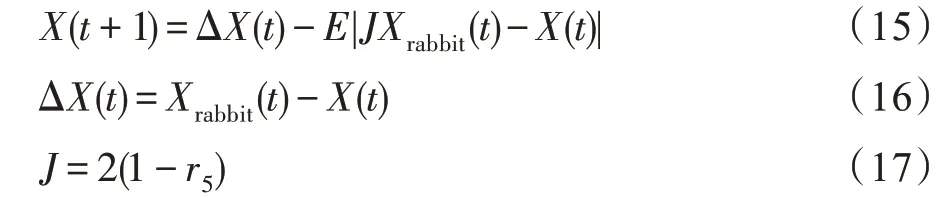
开发阶段硬包围公式为：

开发阶段渐进软包围公式有：

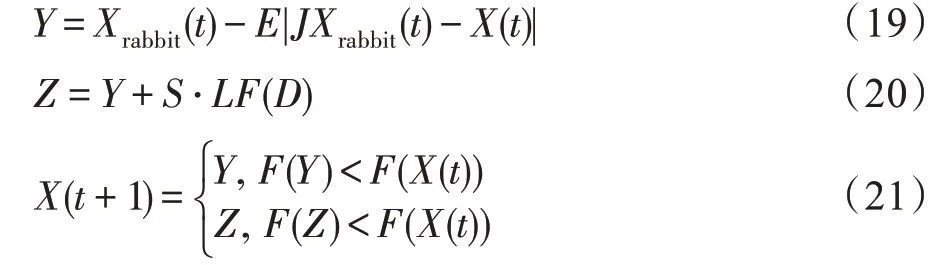
其中，为Lévy 飞行函数，参数取值为1.5。

开发阶段渐进硬包围公式：

开发阶段中Δ为最优个体和当前个体的差值，是0到1之间的随机数，为逃跑过程中的跳跃距离，是问题的维度，是一个维的随机向量。

哈里斯鹰优化算法的大致流程为：初始化种群，将适应度最优的个体设置为猎物，根据逃逸能量和生成的随机数执行全局搜索或局部开发中对应的包围策略。计算每个个体的适应度并与猎物适应度比较，若位置更新后的个体适应度值优于猎物，则以适应度值更优的个体位置作为新的猎物位置，不断迭代直至满足终止条件或达到最大迭代次数算法终止。

自HHO 算法面世后，关于该算法的各种改进相继被提出来，选取了若干改进的方法归纳如表5所示。

除表5 中列举出的各种改进方法外，还有其他的一些改进和应用，如文献[83]中发现逃逸能量因子采用指数递减策略能够有更快的收敛速度和更高的求解精度。哈里斯鹰优化算法在图像分割、神经网络训练等各领域也得到广泛运用。

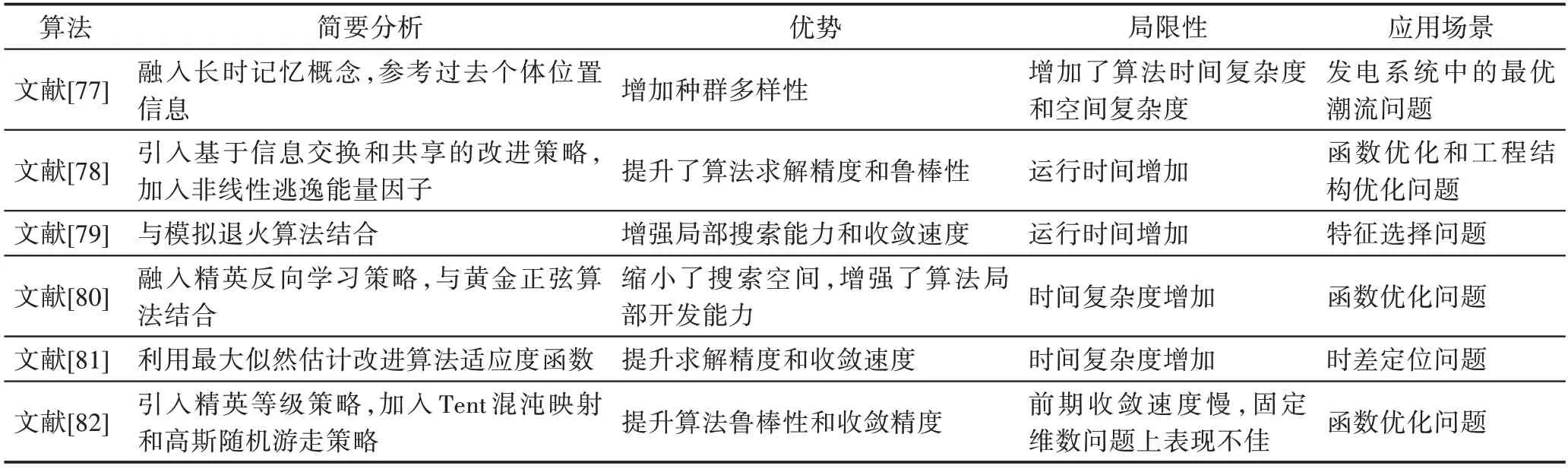
表5 哈里斯鹰优化算法改进分析Table 5 Improvement analysis of HHO

1.6 麻雀搜索算法

麻雀搜索算法（sparrow search algorithm，SSA）是由Xue 等于2020 年提出的群智能优化算法，SSA 算法涉及到的主要公式如式（25）～（27）所示：

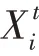
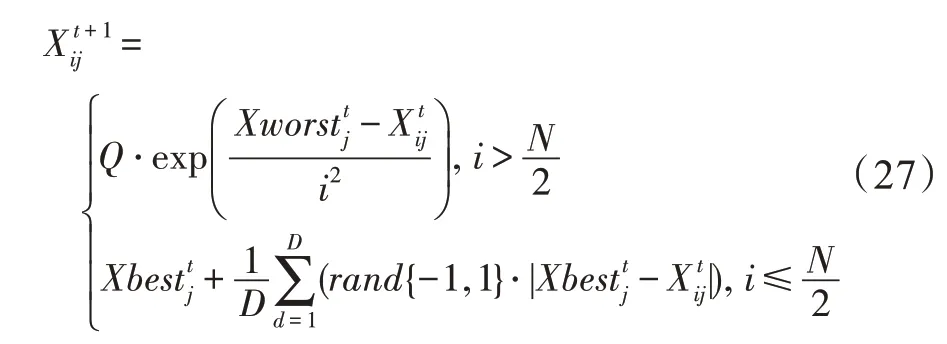
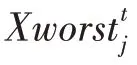
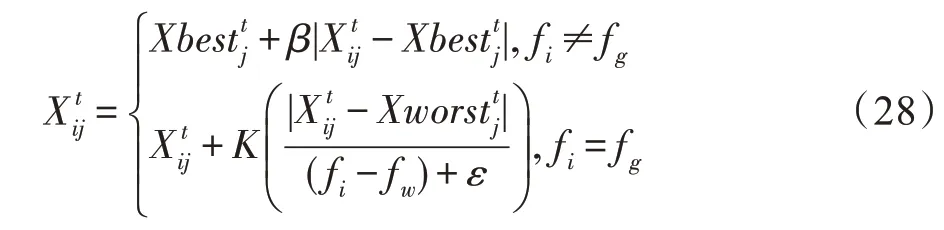
麻雀搜索算法的基本流程：初始化麻雀种群，计算个体的适应度值并排序，找到最佳和最差适应度的个体，依次更新发现者、加入者、警戒者位置，不断迭代更新，直至满足算法终止条件算法终止。

有关麻雀搜索算法的相关改进也有很多，选取了若干改进的方法归纳如表6 所示。

表6 麻雀搜索算法改进分析Table 6 Improvement analysis of SSA

除表6 中列举出的各种改进方法外，麻雀搜索算法还有其他的一些改进和应用，如史春天等归纳的麻雀搜索算法在应用于图像分割时各种有效的改进策略。

2 实验与性能分析

2.1 实验环境及参数设置

为对比分析6 种智能优化算法的优缺点，本文从若干优化文献[95-97]中选取3 种类型共21 个基准测试函数进行仿真实验用于评价算法的性能。其中～为高维单峰测试函数，～为高维多峰测试函数，～为低维度多峰函数测试函数。单峰测试函数可以评估算法的开发能力及开发精度，多峰测试函数可以评估算法跳出局部最优解的能力。各测试函数的详细信息见表7～表9。

表7 单峰测试函数Table 7 Single peak test function

表8 多峰测试函数Table 8 Multimodal peak test function

表9 固定维度测试函数Table 9 Fixed dimension test function

为减少统计误差并产生有说服力的结果，每个算法进行30 次独立实验。实验环境为：操作系统Windows 10，处理器为IntelXeonGold 6154 CPU@3.00 GHz，内存为32 GB，集成开发环境为Matlab_R2017b。种群设置为50，最大迭代次数1 000次，算法所设置的其他初始参数如表10 所示。

表10 算法控制参数的初始值Table 10 Initial value of control parameters

2.2 评价标准

针对21 个基准测试函数，通过算法找到解的平均值、最优值、最差值、标准差、平均运行时间和收敛曲线等六方面评价算法的性能。平均值用于衡量算法的优化精度，最优值和最差值反映解的质量，标准差反映算法的稳定性和鲁棒性，平均运行时间反映算法执行的时间代价，收敛曲线反映算法的收敛情况，综合比较平均值和标准差得到算法的排名，计算算法在21 个测试函数排名的平均值作为Mean rank 值。

2.3 实验结果及分析

统计6 个智能优化算法在21 个基准测试函数上的求解结果得到表11，表中参数mean 表示求解平均值，std 表示标准差，best 代表最优值，worst 代表最差值。分析表11 可知，对于本文选择的21 个测试函数，总体上看，HHO 和SSA 寻优能力明显强于其他算法，且HHO 相较于SSA 效果更好，BOA 和SCA 寻优效果处于中等水平，GOA 和MFO 的求解效果较差。在高维单峰函数～上，HHO 和SSA 表现出优秀的求解精度，所求得解的平均值与全局最优值十分接近，30 次实验中的标准差小，效果最好。BOA 效果较好，平均值和标准差也在可接受的范围内，SCA 和GOA效果一般，MFO 所求得解的平均值与真实的全局最优解有较大差距，多次实验得到的最优值也远不及其他算法，效果最差。在高维多峰函数～上，HHO 和SSA 在函数和中找到了全局最优值，BOA在函数中找到了全局最优值，整体上看，HHO和SSA 效果最好，BOA 效果次之，SCA 和GOA 效果一般，MFO 效果最差，测试结果与高维单峰函数测试的结果基本一致。需要注意的是MFO 在和中，所求得解的平均值与真实的全局最优解有极大差距。在低维多峰函数～上，测试结果与单峰和多峰函数上的结果出现差异，SSA 在5 个函数上取得较好效果，MFO 在2 个函数上取得较好的效果，MFO 和SSA 效果较好，GOA 和HHO 效果次之，BOA和SCA 效果较差。

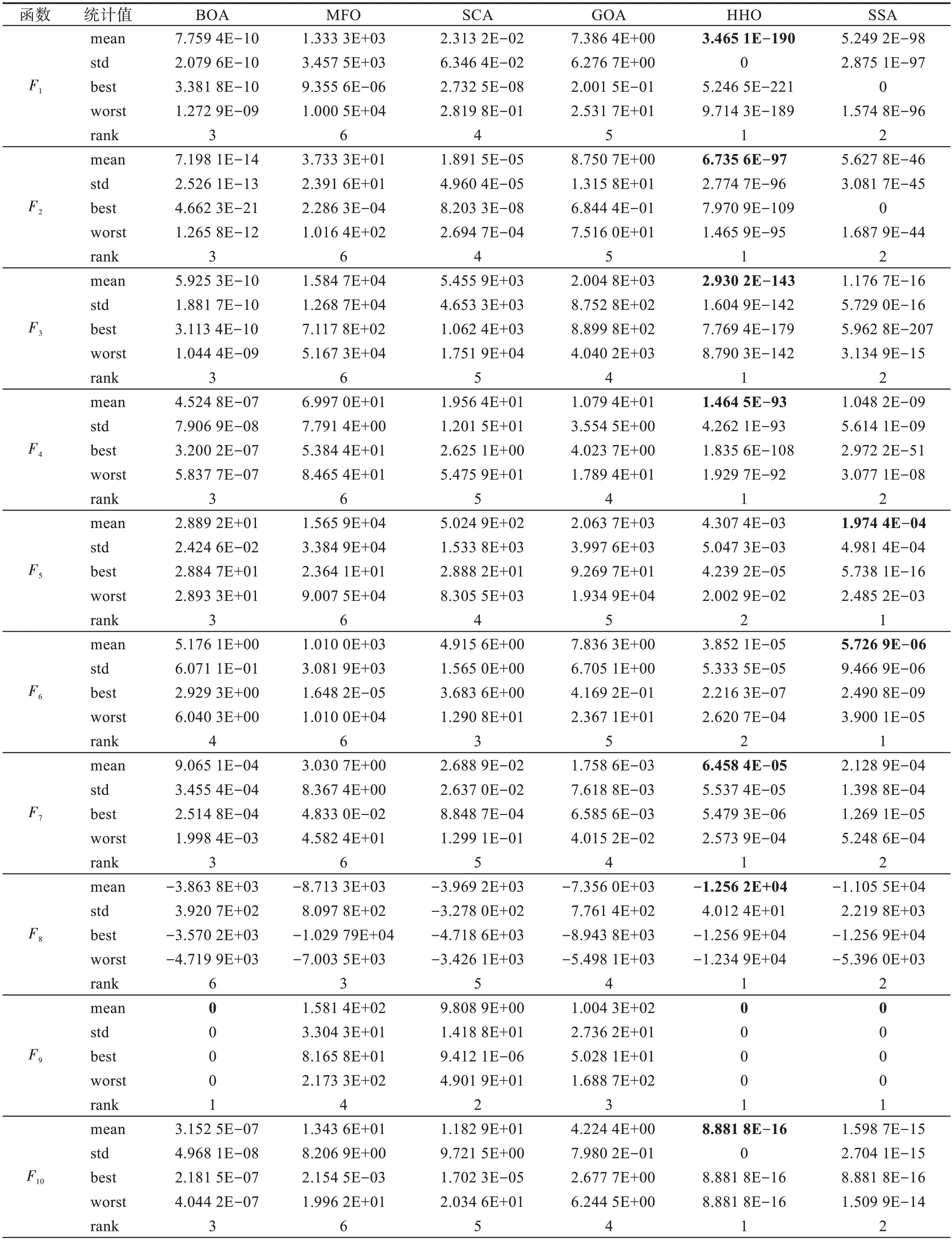
表11 测试函数优化结果Table 11 Test function optimization results

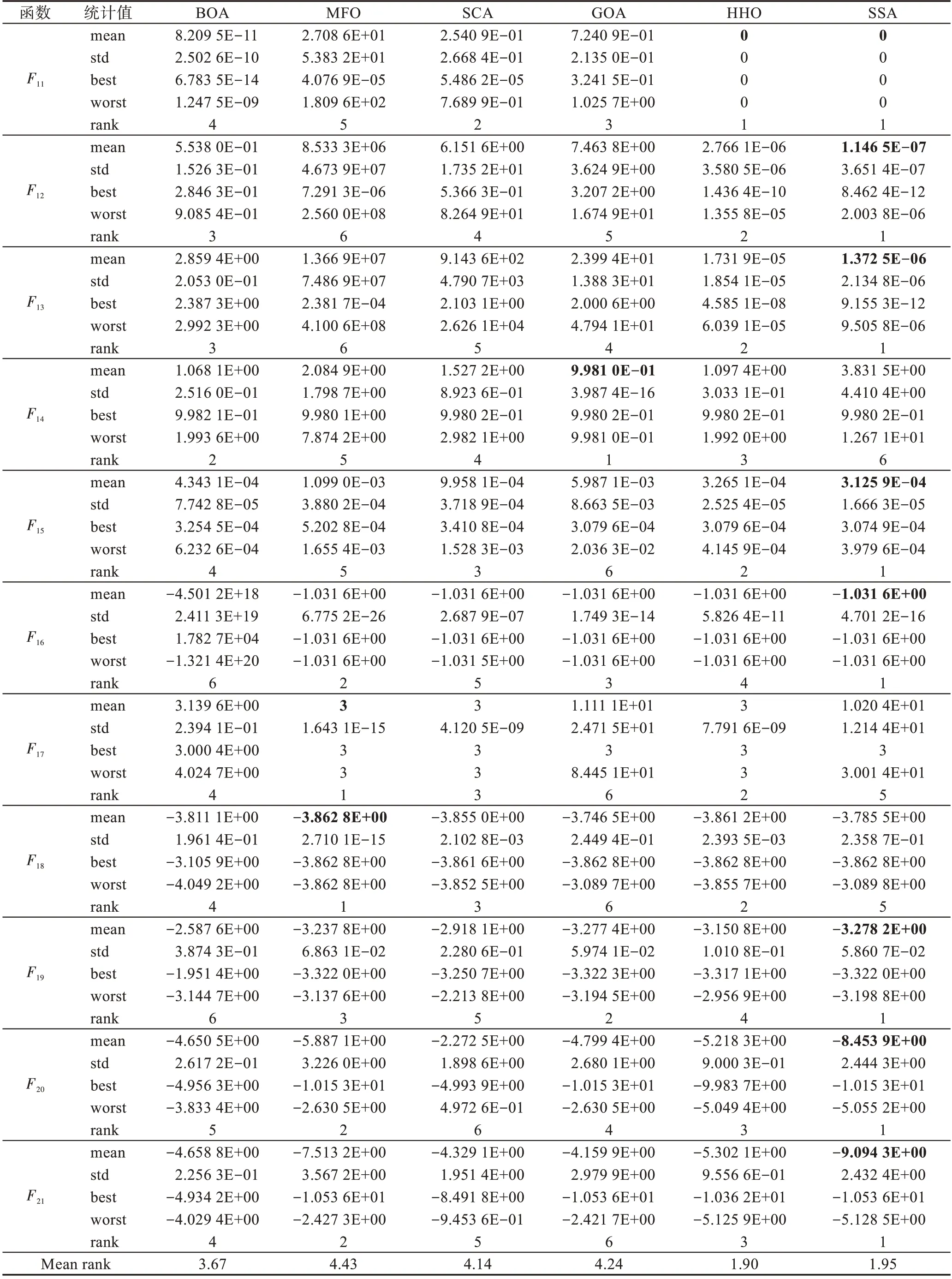
表11 （续）

为验证6 个算法的稳定性与收敛性，列出了各算法在部分单峰测试函数和多峰测试函数上的收敛性对比图，如图1 所示。MFO、SCA 和GOA 算法在处理单峰测试函数和多峰测试函数时均存在早熟收敛现象。哈里斯鹰算法和麻雀搜索算法在少数测试函数中也存在早熟收敛，但求解的精度优于其他算法。哈里斯鹰算法在求解单峰测试函数、、和时，迭代至750 次左右收敛，此时的求解精度远好于其他算法。蝴蝶搜索算法在多峰测试函数、、时性能表现较好，随迭代次数的增加求解的精度不断提升。哈里斯鹰算法和麻雀搜索算法在求解多峰函数和时，迭代到300 次左右找到了全局最优解，在其他多峰函数上的求解精度也高于其他算法，说明这两个算法能在全局搜索和局部开发间维持较好的平衡。

根据图1 纵向分析，在相同的迭代次数下，哈里斯鹰算法和麻雀搜索算法可以取得较高求解精度；根据图1 横向分析，各算法达到相同求解精度时哈里斯鹰算法和麻雀搜索算法只需要较少的迭代次数便能实现。在BOA 算法中蝴蝶有两种搜索方式，全局搜索时向着香味浓度最高的蝴蝶飞行，局部开发时在种群中随机选择一只蝴蝶向其移动。通过分析图1 可以发现，蝴蝶优化算法在处理测试函数时，收敛精度不高，整个群体虽然向着解中心聚集，但多次迭代浪费在随机找蝴蝶移动上，种群多样性一旦降低，没有相应策略帮助跳出局部最优解，即使增加最大迭代次数，效果提升也不大。结合表11 可以看出，BOA 在求解函数时表现出极大的误差，不是算法求解效果都差，而是在实验中某次产生的巨大误差拉大了多次实验求解的平均值，说明BOA 算法存在一定的不稳定性。MFO 算法中以对数螺线的更新机制更新飞蛾的位置信息，与蝴蝶优化算法相比，蝴蝶算法的位置更新目标在最优蝴蝶和随机蝴蝶中选择，而飞蛾的位置更新则是以火焰为基准，随迭代次数的增加，飞蛾与火焰间的距离变短，飞蛾飞行的振幅越来越小，逐渐由全局搜索转向局部开发，同时火焰数量的减少也带来种群多样性降低，在求解多峰函数时多次较早陷入局部最优。再结合表11 不难看出，MFO 在函数、、求解中出现了巨大误差，稳定性比BOA 更差。正弦余弦优化算法基于正弦和余弦数学模型在求解过程中使得种群向外或向最优解的方向波动，算法原理简单，所需初始参数少，利用多个随机变量和控制参数来计算当前解所在的位置，全局搜索能力强但搜索精度不够，随迭代次数的增加控制参数逐渐减小，使得正弦余弦算法函数振动幅度变小，全局搜索能力减弱，局部开发能力增强，同时带来种群多样性降低的问题，种群个体聚集在搜索空间的一个或几个位置，结合在、、、函数上的收敛曲线，进一步证实算法容易出现早熟收敛现象。蝗虫优化算法中参数的作用是平衡算法全局搜索和局部开发的过程，自适应减小蝗虫间的排斥力，用以提升种群密度。在蝗虫位置更新过程中，位置差的蝗虫出现适应度值一直波动的情况，适应度值下降缓慢，且适应度值差的蝗虫也参与蝗虫位置的更新，对位置较好的蝗虫产生了干扰，降低了算法的收敛速度。如在、、、、函数上的收敛曲线出现陷入局部最优的现象。哈里斯鹰优化算法中有4 个位置更新策略，可以根据猎物的行为做出必要的调整，通过一个能量逃逸因子和一个随机数来决定使用哪个包围策略，有更强的普适性。在所选取的21 个基准测试函数中，除去、、、、外均有优秀的求解效果，在处理高维单峰测试函数∼时，迭代750 次左右完全收敛，在高维多峰测试函数上也比其他算法收敛得更快，求解精度更高。麻雀搜索算法通过将种群个体分为发现者、追随者和警戒者3 个角色，各角色有不同的功能，在测试函数上表现出很强的寻优能力，在某些测试函数如、、、上效果比HHO 算法更优秀。但麻雀算法收敛于最优解的方式是部分发现者直接跳跃至当前最优解附近，收敛速度快的同时使得种群多样性迅速减少，因此麻雀搜索算法仍存在容易陷入局部最优的问题。HHO 算法个体位置更新公式（15）和SSA 算法个体位置更新公式（25）中都存在向原点靠近的行为，这一行为使得两个算法在算法执行到算法后期时，整个种群大致分为两个群体，一部分聚集在原点附近，另一部分聚集在当前最优解附近。麻雀搜索算法位置更新策略相较于哈里斯鹰算法更为单一，当全局最优解在原点附近时可以取得较好的求解效果，而哈里斯鹰算法中的4 种包围策略对于全局最优解不在原点附近的优化问题也能进行不错的求解，因此HHO 对于问题的普适性优于SSA 算法。

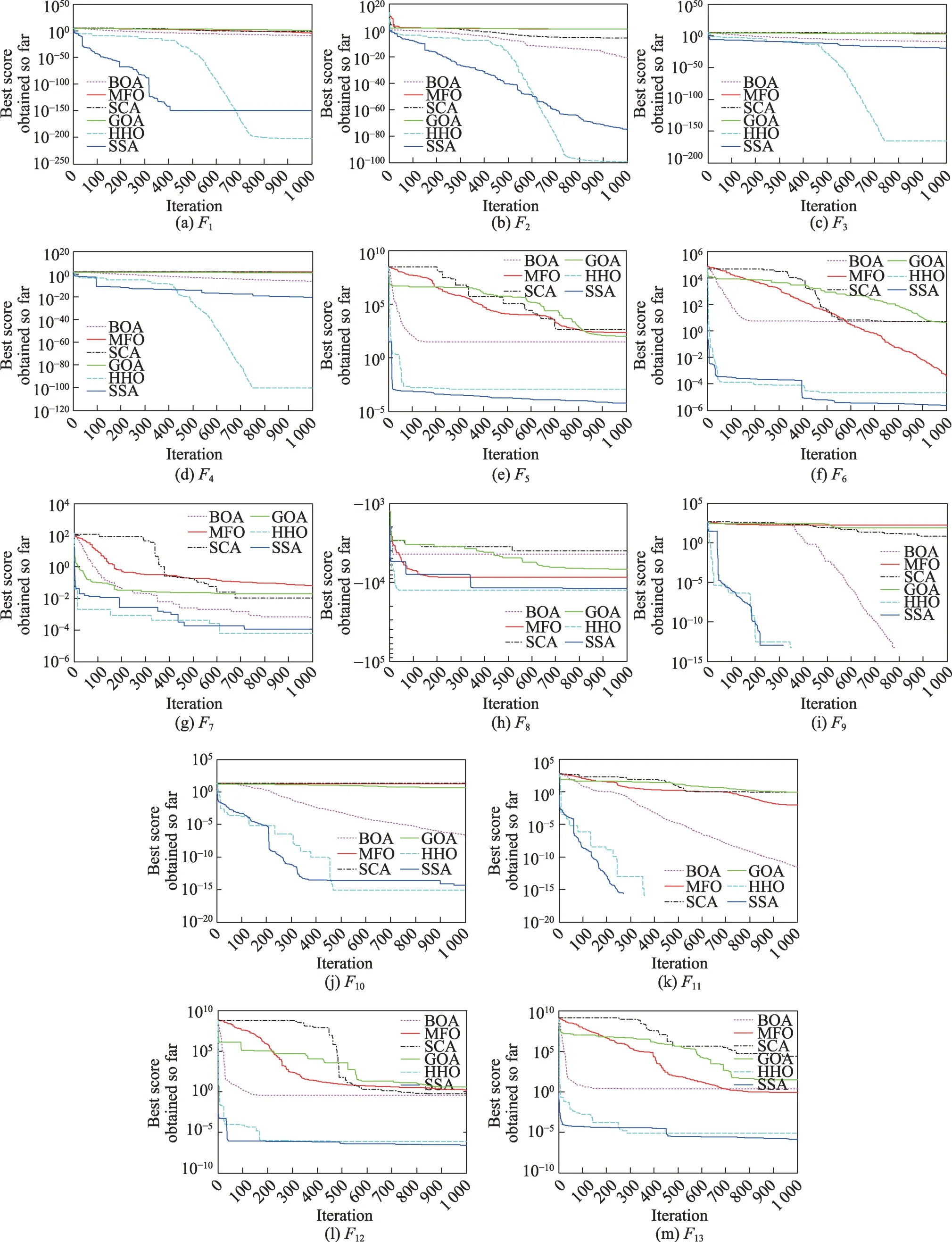
图1 各算法在测试函数上收敛曲线对比Fig.1 Comparison of convergence curves of each algorithm on test functions

统计各算法在测试函数上的运行时间得到表12。通过表12 可以看出，6 个算法平均执行时间最短的是正弦余弦优化算法，执行时间最长的是蝗虫优化算法。正弦余弦优化算法中，使用一个线性递减的控制参数改变函数的振幅帮助寻优，相较于其他算法没有单独设置跳出局部最优的步骤，很大程度上降低了算法的时间复杂度。而蝗虫优化算法中，每只蝗虫个体位置信息的更新都需要除它本身之外其余所有蝗虫的位置信息，与其他算法相比个体更新位置的成本更大，时间复杂度更高，因此耗费的时间也更多。

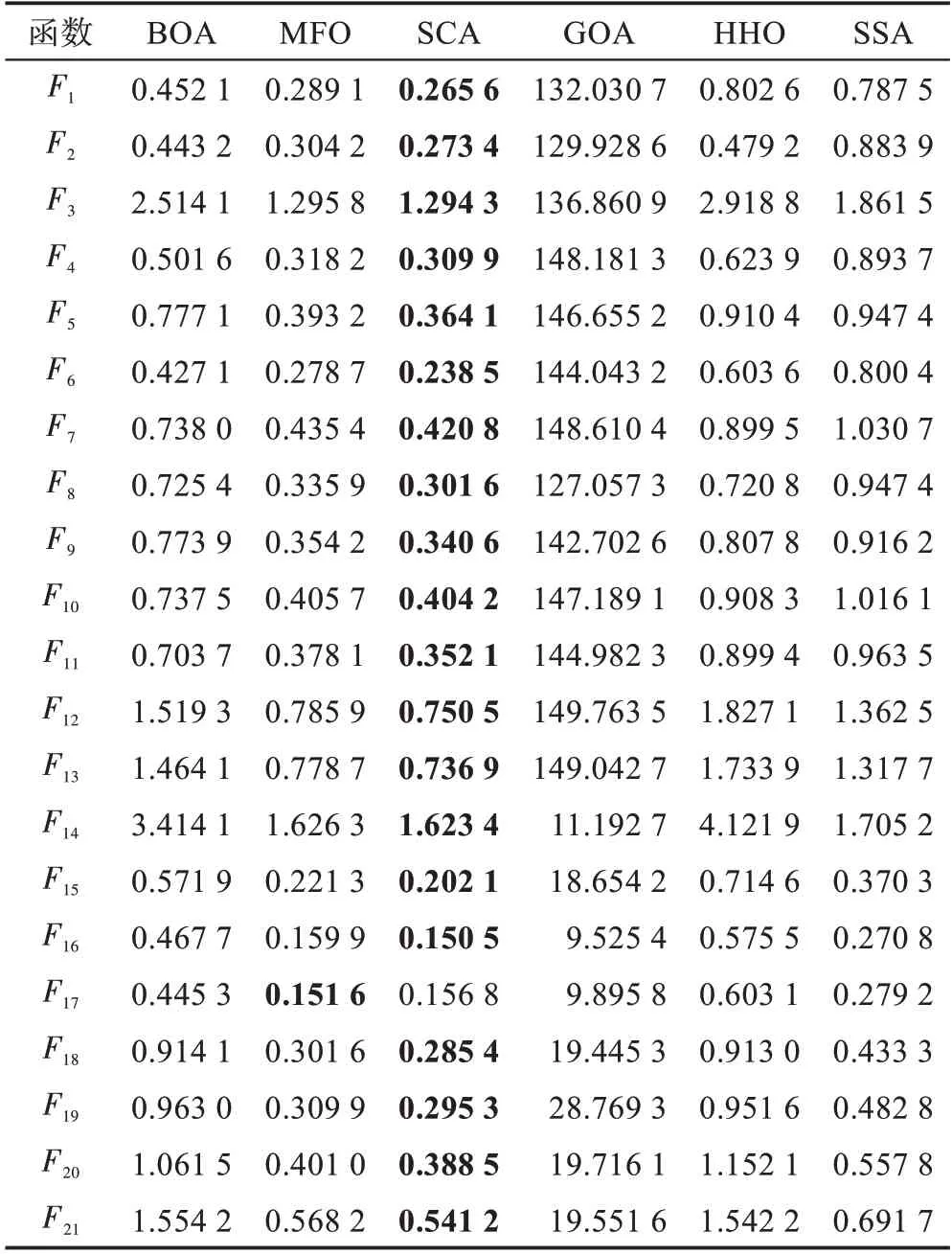
表12 各算法的执行时间Table 12 Execution time of each algorithm s

结合6 个算法在21 个测试函数上的表现，从求解平均值、标准差、最优值、最差值、收敛曲线和运行时间等各个方面定性分析算法的寻优能力，可以发现在6 个算法中，蝴蝶优化算法在解决具有多个局部最优解的问题上表现出较好的精度，在寻优能力和求解时间上明显优于一些经典的智能算法，原理简单，易于实现，没有明显的短板。飞蛾扑火算法在求解高维测试函数时容易出现较大误差，但求解低维多峰问题时求解效果较好，时间成本不高，适合应用于工程实践中的参数优化。正弦余弦优化算法求解时所消耗的实践成本明显低于其他算法，适合应用于对精度要求不高，但对时间要求严苛的场景中。蝗虫优化算法存在时间成本高，求解精度不佳等问题，但若将其改进为分布式计算方式，可大幅度降低求解的时间成本。哈里斯鹰优化算法在运行时间和求解精度上优于其他5 个算法，跳出局部最优的能力强，在应对复杂问题时有更高的包容性，但其算法构成复杂，对于具体实际问题进行算法实现时具有一定难度。麻雀搜索算法在提升求解精度的同时运行时间并未大幅度增加，应对全局最优解靠近原点附近的优化问题时能表现出优秀的性能。需要注意的是本文得出的结论只是基于实验所得的数值结果，各算法的具体求解性能还要依据实际问题进行分析。

智能优化算法的寻优过程总体可以分为两部分，全局搜索和局部开发。这两部分相互促进又相互矛盾，全局搜索用于快速定位最优解的范围，而局部开发用于锁定最优解存在的区域并进一步寻找最优解，只有两部分达到一个良好的平衡状态才能有较好的求解效果。当算法偏重全局搜索时，算法执行慢，效率低，很难找到一个满意的解，尤其是问题规模达到一定程度，这种缺陷显得更为突出；而算法侧重于局部开发时，会降低种群多样性，使算法容易陷入局部最优。对智能优化算法的改进多数也是从这两个角度入手，具体算法的改进要依据实际问题具体分析。设计出收敛速度快，求解精度高，跳出局部最优能力强，且普适性、鲁棒性和稳定性优秀的智能优化算法是学者们不断追寻的目标。

3 结束语

本文挑选了2015 年以来提出的六种新型智能优化算法，详细阐述了每种智能优化算法的基本原理和算法流程，梳理了相关的改进方法和应用场景，并通过基准测试函数从求解平均值、标准差、最优值、最差值、收敛曲线和运行时间六方面分析了算法的寻优能力，对比发现近两年提出的哈里斯鹰算法和麻雀搜索算法在求解精度、收敛速度、执行时间等方面有较好的效果。目前智能优化算法处于快速发展的时期，针对不同领域不同类型的问题不断有新的智能优化算法被提出来，这些智能优化算法的涌现为解决优化问题提供了新的思路和灵感。未来的智能优化算法在实际应用和工程领域将会有更广阔的应用前景。