2014—2020年拉萨市环境空气质量评价分析

洛桑卓嘎 四郎措姆 格桑卓嘎 旦增克珠 洛桑

(1.拉萨市气象台，西藏 拉萨 850000；2.米林县气象局，西藏 林芝 860500)

随着工业化和城市化进程不断推进，近几年全国范围内各大城市均出现环境空气污染问题，城市空气质量问题愈发严重，日益引起社会广泛关注。西藏和平解放70年来，拉萨市经济社会发展成就显著，城市化建设步伐不断加快，但伴随着工业和交通等基础设施大力建设以及燃油机动车保有量的大幅增加，对城市环境空气质量也造成一定影响；再加上全球变暖背景下，青藏高原天气气候系统变化明显，也给城市空气污染问题带来不确定影响，因此，对拉萨市环境空气质量的评价研究工作十分必要。目前，国内外许多学者在环境空气质量这一领域的研究工作取得了较大进展，如付强等[1]研究了主成分分析在环境空气质量评价中的应用；黄战胜等[2]对宝鸡市近年来大气质量变化趋势进行了分析；李冰月、周新宇等[3]以北京白塔寺街区为例基于主成分分析法对历史文化保护区的空气质量进行评价；张春辉等[4]对2003—2014年贵阳市环境空气质量变化趋势进行了分析；刘萍等[5]基于主成分分析法对空气质量评价方法进行了研究；祝新明等[6]对2014—2018年桐乡市环境空气中6个主要指标完成评价分析；韩卓等[7]基于AHP模型对西安市大气质量进行了评价分析；程涛等[8]基于小波分析法对上海市环境空气质量变化及与气象的关系进行研究。本文借鉴上述文章的分析研究方法，主要使用主成分分析法对2014—2020年拉萨市的空气质量进行评价分析，并利用Spearman秩相关系数法对2014—2020年拉萨市的6类污染物变化趋势进行分析。

1 资料来源及方法

1.1 数据说明

本文所用的资料为2014—2020年拉萨市环境监测站的6类空气污染物的逐日浓度值数据。该数据来源于天气后报网站上的空气质量相关数据，该网站上的数据均来源于国家环境监测总站，因此数据真实有效。

1.2 分析方法

本文主要使用主成分分析和Spearman秩相关系数法(Daniel趋势检验方法)两种分析方法。

主成分分析(PCA)是1901年由卡尔·皮尔逊发明的一种统计方法，它使用正交变换将一组可能相关变量(实体，每个实体具有不同的数值)的观察值转换为一组称为主成分的线性不相关变量的值。主成分分析是最简单的基于特征向量的多元分析，它通过降维技术，客观处理各个指标的权重，使评价结果更加客观。本文主要使用SPSS22.0进行主成分分析。

党的十八大提出“五位一体”建设布局，将生态文明建设和经济、政治、文化、社会建设放在同等重要的位置。水资源保护是生态环保的重要内容，引起全社会的高度关注。水污染防治行动计划在其首要任务“全面控制污染物排放”里，除了控制工业污染、城镇生活污染、农业农村污染外，明确了要加强船舶港口污染控制。《水污染防治行动计划实施情况考核规定（试行）》已将“船舶港口污染控制”纳入政府考核体系，考核本地区港口和船舶污染物接收、转运及处置方案的编制情况和方案建设内容完成的进度。

本文对空气污染物的变化趋势分析主要采用Spearman秩相关系数法(Daniel趋势检验方法)利用天气后报所提供的日平均数据求出各污染物的年平均浓度进行趋势变化分析。

2.3 提高了作为住院医生的整体素质 我院在2014年和2015年这两年连续开展住院医师系统培训工作，通过培训，住院医师的临床技能动手能力和临床思维分析能力比没参加住院医师系统培训工作的医师明显提高。参加国家统一执业医师考试的成绩：2014年14人参加，13人通过，2015年11人参加，10人通过，两年的通过率达92%；2012年4人参加，2人通过，2013年4人参加，2人通过，2016年9人参加，4人通过，三年的通过率仅47%，见表1。对两组参加考试人员的通过率χ2检验，χ2=10.572，P=0.001，经系统培训后的医生参加国家统一执业医师考试的通过率明显提高。

取得重大勘探发现尤其是前沿领域的勘探突破是每个石油公司追求的目标，但勘探天然伴随着风险，而国际大石油公司大都实行规避风险的严格资本支出原则。在此种情形下，国际大石油公司采取自身寻求油气发现，以及在已有油气发现的前沿领域寻求早期快速切入相结合的方式。这可以看作做是大石油公司在高风险前沿领域平衡效益与风险的策略。大部分国际大石油公司采取这种策略，只有埃尼采取进攻策略，追求在前沿领域通过自己勘探实现油气发现。

2014—2020年拉萨市区O3、NO2、PM10、PM2.5、SO2、CO的年均浓度值(表5)(单位：NO2、PM10、PM2.5为μg/m3；O3、SO2、CO为mg/m3)

通过以上步骤我们已经获得了两个主成分的特征向量值，因此我们可以求出两个主成分的得分，并利用综合评分法求出空气质量综合评价表(表4)。

将秩相关系数γs的绝对值同Spearman秩相关系数统计表中的临界值Wp进行比较。|γs|>Wp则表明变化趋势有显著意义。如果γs是负值，则表明在评价时段内有关统计计量指标呈下降或好转趋势；如果γs为正值，则表明在评价时段内有关统计计量指标变化呈上升或加重趋势。|γs| ≤Wp则表明变化趋势没有显著意义，说明在评价时段内空气质量变化稳定或平稳。

2 结果及评价

2.1 空气质量评价

从表3可以看出：主成分1与所有污染物呈正相关关系，而其中PM2.5、PM10的特征向量的绝对值较大，其中PM2.5的值最大，因此PM2.5为首要污染物。主成分2与PM2.5、PM10、NO2呈负相关关系，与SO2、CO、O3呈正相关关系，并且SO2、NO2、CO的特征向量绝对值较大，其中NO2的特征向量最大，为首要污染因子。

晨起未及时排尿：睡了一晚上，要及时把尿液排出，因为它们堆积大量毒素。人体五脏都是相互影响的，喜欢憋尿不及时排尿的人，除了容易患上泌尿系统疾病、肾病之外，毒素的大量聚积都要跟负责解毒的肝脏联系起来，进而影响肝脏健康。

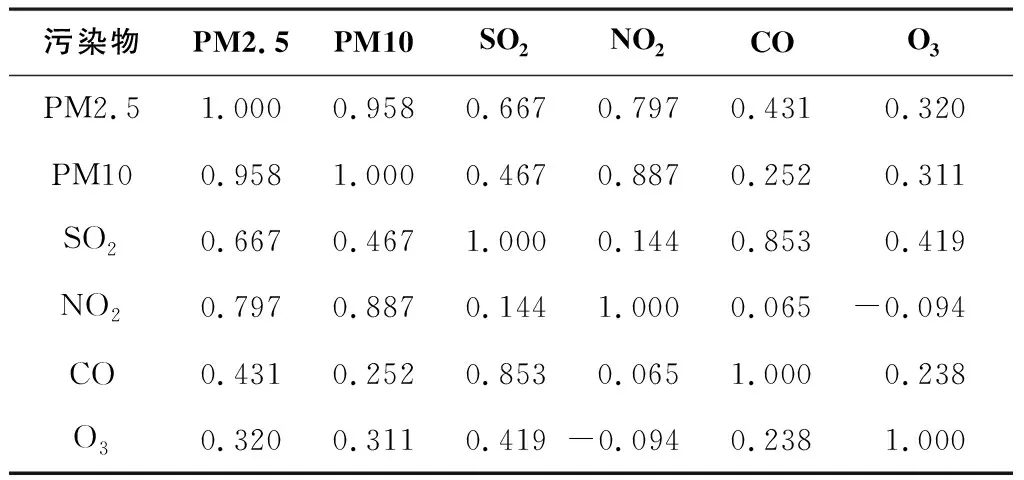
表1 相关系数矩阵

表2 解释总方差

通常线性相关系数大于0.7说明线性相关较高，并且越接近1越相关。从表1可以看出，PM2.5与NO2、PM10的相关性较大，SO2与CO的相关性较大。

重构后对应的网络结构如图8所示。求得最优解断开的支路为：7-8，9-10，14-15，32-33，25-29，此时网络结构的网损为129.830 9 kW。

当特征值大于1且累计方差贡献率超过80%则表明主成分的解释力度足以代替原来指标的解释力度。从表2中可以看出：成分1和成分2的特征值分别为3.409和1.589，并且累计方差贡献率达到83%，并且成分1的特征值大于成分2，因此在这两个主成分中成分1为主导成分。

本文主要通过主成分分析法对2014—2020年期间拉萨市的6类监测污染物年浓度值进行评价，经过分析得出污染物的KMO和Bartlett的检验结果，并显示Bartlett球形检验的显著性P值为0.00，小于0.05，说明数据适合做因子分析，并得出污染物之间相关系数矩阵(表1)、解释总方差表(表2)、成分矩阵表(表3)、拉萨市2014—2020年环境空气质量综合评价表(表4)。

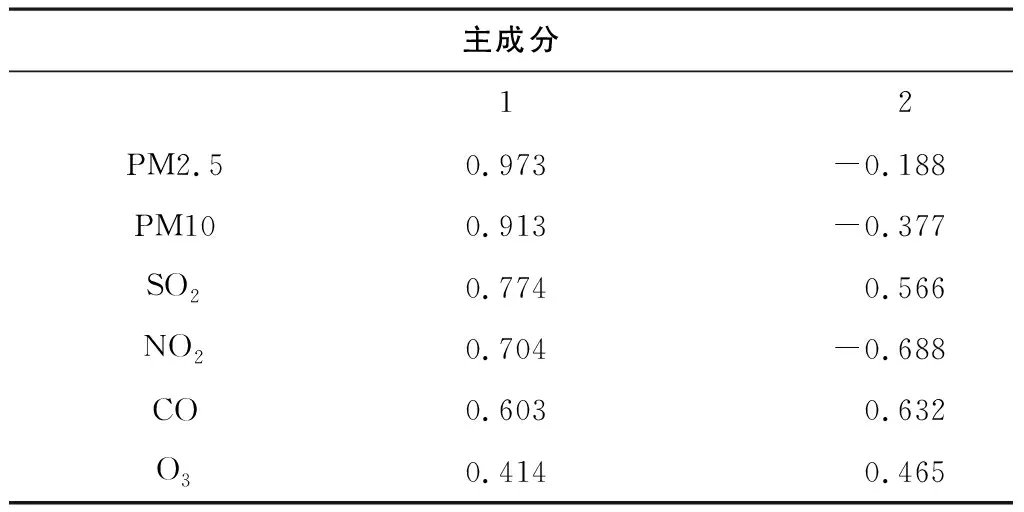
表3 成分矩阵

BIM技术在施工阶段的应用主要体现在造价控制上。首先，在施工阶段承包方往往会依据施工进度来计算工程量，但是这一过程存在着延迟，使得工程量的核算结果与实际工程量之间出现差异，不仅难以保障造价核算的精确度，还会造成资源浪费。而在施工过程中使用BIM技术，优秀的建模能力和可视性能够简化施工流程，更好地帮助施工团队编制核算工程量；其次，BIM技术应用可以在施工过程中跟踪市场行情变化，及时将材料价格、运输价格变动及机械使用费用数据编辑在模型中，有利于施工方进行动态维护。最后，BIM技术能够通过自带的绩效和费用核算功能对工程造价进行及时分析，帮助施工团队规避费用偏差。

传统的教学模式下，教师在课堂中大多以填鸭式的教学方法展开授课，在一定程度上忽略了学生的主体性，容易影响学生对于数学学习的积极性，导致目前小学数学教学中存在一些问题，大部分小学生不能高效的学习数学知识，甚至有些学生对数学学习具有反感心理。随着我国教育的不断发展，体验式学习方法逐渐得到学科教学的应用，如何在教学中合理应用体验式学习方法成为小学数学教师所面临的关键问题，对于教学水平的提高具有积极意义。

表4 拉萨市2014—2020年环境空气质量综合评价表

年际变化是对2014—2020年的PM10、PM2.5、SO2的年最大日均浓度、年最小日均浓度、年平均日均浓度值进行统计并计算秩相关系数，可得出PM10的γaverage=-0.9