十自由度车-轨耦合仿真分析

熊勇刚 龚琦

摘要： 文章以十自由度车轨耦合模型为例，探究由轨道不平顺所导致车-轨耦合垂向振动的问题，由功率谱密度计算确定了轨道不平顺并以此作为激励源，计算分析车辆与轨道之间的垂向耦合振动响应。通过MATLAB仿真结果图分析得出，轨下的高底不平顺主要影响的是构架和轮对的振动频率，对车体的影响并不大，因此要减轻车-轨系统的振动主要从一系悬挂和轮轨的接触两个方面考虑。

Abstract： Taking the ten degree of freedom vehicle rail coupling model as an example， this paper explores the problem of vehicle rail coupling vertical vibration caused by track irregularity， determines the track irregularity by power spectral density calculation， takes it as the excitation source， and calculates and analyzes the vertical coupling vibration response between vehicle and track. Through the analysis of MATLAB simulation results， it is concluded that the high bottom irregularity under the rail mainly affects the vibration frequency of the frame and wheel set， and has little impact on the vehicle body. Therefore， to reduce the vibration of the vehicle rail system， it is mainly considered from the two aspects of primary suspension and wheel rail contact.

关键词： 车-轨垂向耦合;轨道不平顺;振动分析

Key words： vehicle rail vertical coupling;track irregularity;vibration analysis

中图分类号：U461.1                                          文獻标识码：A                                  文章编号：1674-957X（2022）03-0023-05

0  引言

轨道交通系统内的轮轨垂向纵平面内存在大量的振动激扰源，具体的可以分为轨上部分和轨下部分，轨上部分又可以分为局部凹凸不平顺、周期性不平顺、脉冲型不平顺等。以上所述不平顺的表现形式，局部的如：轨头压陷、轨面剥离等;周期性的如：波形线路、波浪形磨耗钢轨、偏心车轮等[1];脉冲型的如：焊缝、低接头、大轨缝等。而轨下基础也会有着如扣件失效、轨枕空悬、道床固结和各种连接段的刚度突变等。这些因素均会对轮轨系统相互作用造成影响，具体表现就是车轨系统产生振动冲击，使得车辆运行稳定性下降，甚至危及行车安全并直接影响轮轨系统的日常养护维修工作量[2]。由此，探索轮轨垂向动态的相互作用，以及影响轮轨耦合振动的因素，寻求抑制或解决方法是车辆-轨道垂向耦合动力学的重要研究内容。

文章以十自由度车辆模型和弹性支撑式轨道为例，进行车-轨垂向耦合模拟，探究轨下高低不平顺对车轨系统的振动影响。

1  车辆模型

1.1 车辆模型

列车是一个由轮对、转向架、车体和弹簧阻尼装置等各个部件组成的综合系统，因此它具有多个自由度。而进行车轨耦合研究时，根据轨道上下做出分解将列车视为一个整体考虑，为简化分析过程，车辆模型[3]作如下假定：

①考虑到实际情况和仿真需求我们可以将车体、转向架、轮对视作不进行弹性变形的刚体。②车轮与转向架、车体与车架之间的弹簧阻尼连接分别称为“一系悬挂”和“二系悬挂装置”。此外，一系和二系减振器均具有粘滞阻尼和摩擦阻尼特性。③仅考虑车体、转向架和轮对沿车辆横轴方向的振动。④根据垂向仿真的实际需求，车体模型自由度限制为沉浮，转向架自由度限制为沉浮及点头，轮对则只考虑沉浮。故总体自由度数量为十。

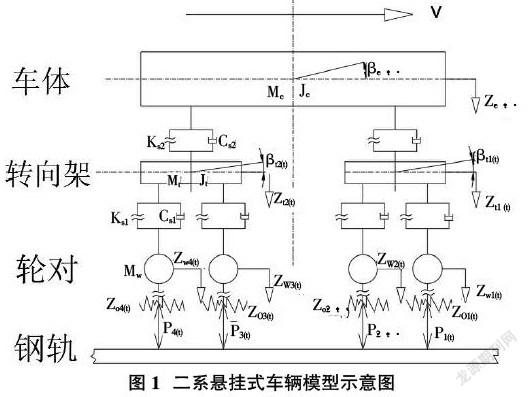
二系悬挂式车辆模型建立如图1所示。

图中各字母所表示含义如下：

Mc：车体质量（kg）;Jc：车体点头转动惯量（kg·m2）;Mt：构架（转向架）质量（kg）;Jt：构架（转向架）点头运动惯量（kg·m2）;Mw：轮对质量（kg）;Ks1：车辆一系悬挂刚度（N/M）;Cs1：车辆一系悬挂阻尼（N.S/M）;Ks2：车辆二系悬挂刚度（N/M）;Cs2：车辆二系悬挂阻尼（N.S/M）;Zc：车体竖向位移（m）;Zt1，2：前后转向架竖向位移（m）;Zw1-4：四个轮对竖向位移（m）;βc：车体点头角位移（rad）;βt1，2：前后转向架点头角位移（rad）;ZO1～4：四个轮对下轨道不平顺（m）;P1～4：单侧车轮的轮轨垂向作用力（m）;Foi（t）：各轮对处激振力函数（i=1～4）。

1.2 车辆运动方程

结合图1所示的模型简图分别对车体、转向架、轮对应用DAlembert原理得到[4]振动微分方程，具体如下：

2  轨道模型

2.1 弹性支撑式轨道

本文以弹性支撑式轨道为例。示意图如图2。

在建立数学模型前必须简化示意图。简化方式如下：用Euler梁来模拟[5]钢轨;质量块单元模拟混凝土支撑部分;铁轨下面的橡胶垫简化成弹簧阻尼单元;支承块下面的橡胶垫板和橡胶套靴筒可以看成一个弹簧阻尼单元;视混凝土道床板和道床为同一部分，对模型进行相应的简化之后使得计算量减小很多，其简化后的模型如图3所示。

图中各个字符含义如下：

mr：单位长度钢轨的质量（kg/m）;Ms：支承块质量（kg）;EI：钢轨抗弯刚度（N/m2）;Kp：轨下胶垫垂向刚度（N/M）;Cp：轨下胶垫垂向阻尼（N.S/M）;Kb：块下胶垫垂向刚度（N/M）;Cb：块下胶垫垂向阻尼（N.S/M）;Zr：钢轨垂向位移（m）;Zsi：第i号支承块垂向位移（m）。

2.2 钢轨振动方程

建立钢轨振动方程时视钢轨为有限长简支梁，而当计算长度取的足够长时，就可以得到相对合理的结果[6]。例如，给定长度1的计算，计算模型如图4所示。

N：长度l范围内支承块支点总数;Frsi（i=1～N）：一支承块支点反力;lc：车辆定距之半;lt：转向轴固定轴距之半;x0：初始时刻第四车轮的固定坐标;t：运行时间;Zr（x，t）：钢轨的振动位移变量。

3  轨道不平顺的数值模拟

车-轨的相互作用造成了轮轨系统激励[8]。造成这种相互作用的因素有很多，本文主要是针对考虑轨道的几何不平顺进行分析。

计算时输入的轨道不平顺为时域信号，与一般情况下轨道随机不平顺功率谱密度形式差别较大，故仿真计算之前需要转化功率谱密度为时域样本。

对于时频转换[9]一些已经存在的数值模拟方法，例如：二次滤波法、三角级数法等均存在着不同影响程度的问题。目前，一种相对较新的算法是根据功率谱计算谱的振幅和随机相位，之后进行傅里叶逆变换（IFFT）得到时域模拟样本[10]。

具体步骤如下：

①给定某时间序列{XS}，S=1，2，3…N-1，设时域信号的记录长度为T=NΔt，采样时间间隔为Δt，相关函数的时延τ=rΔt也为离散值。离散采样功率谱密度函数，构造X（k），然后进行傅里叶逆变换（IFFT）得到时域的轨道不平顺函数x（t）。

②转换轨道不平顺的功率谱密度函数的单侧谱为双侧谱Sx（f）。

设λmin为轨道不平顺的最短波长，λmax为最长波长，vmax为车辆运行的最大速度，fmax=vmax/λmin是最大时间频率，fmin=vmax/λmax为最小时间频率。由于车辆振动的最大固有频率约为1Hz，为保证fmin<1HZ。由采样定理，采样周期ΔT≤l（2fmax）。设模拟的总时间为Ts，时域采样点的数目应为Ts/ΔT，为了保证采样点的个数为2的整数幂，在端点加0，即Nr由周期图法估计出的功率谱具有周期性，且为偶对称序列。设Nf=（fmax-fmin）/Δf为有效频率段内的采样点数，而Δf=1/（NΔT），设N0=fmin/Δf，则0～（N0-1）和Nf～Nr/2采样点值记为0。于是有功率谱Sx（f）的Nr/2个离散采样点值Sx（f=kΔf），（k=1，2，3…Nr/2）。形成以Nr/2为对称中心的偶对称序列Sx（f=kΔf），（k=0，1，2，3…Nr-1）。

通过查询相关资料，以美国第六级轨道相应数据进行仿真，设车辆速度v=100km/h，如图5所示，其中图（a）只考虑了轨道高低不平順这一种情况，图（b）则是轨道水平和规矩不平顺着两种影响因素。

4  车辆-轨道垂向耦合关系

垂向平面内，综合上述模型建立车辆和轨道之间的耦合模型[11]。车轨之间以轮轨垂向接触实现耦合作用，此时可以应用Hertz非线性弹性接触理论[12]，来确定轮轨之间的垂向作用力。

5  仿真计算

设定车辆类型为B型车，60kg/m钢轨，弹性支承块式无碴道床[13]。利用轨道高低不平顺作为振动激励源对车-轨耦合做垂向振动分析，通过MALTAB的仿真计算，得到了下图，如图6（a）、（b），图7（a）、（b），图8（a）、（b），图9（a）、（b）、（c）所示。

6  结论

通过分析以上图形得出以下结论：

①通过对图6（a）、（b）进行分析，车体的垂向振动加速度和振动能量的峰值都比较接近于车体的自振，所以轨道高低不平顺对车体的影响比较小，甚至在某些情况下可进行忽略。

②图7图8所示，构架振动中低频为主，高频振动相对较少，而轮对则以高频振动为主。构架在低频处的振动可能是由于受到车体与轮对的同时影响，可以发现轮对的振动是影响构架振动的主要因素，故一系悬挂装置是车轨垂向耦合振动的重要考虑点。

③对比图9（a）、（b）、（c）三张图，分析出车体、轮对与构架他们的振动平衡位置是不相同的。车体的平衡位置相较于构架和轮对来说比较大，大约在293mm左右，最大振幅则比构架和轮对较小在2.5mm左右;构架的平衡位置小于车体但大于轮对大约在51mm左右，最大振幅也处于中等在4mm左右，轮对平衡位置最小在0mm左右，最大振幅最大约为5mm。综合分析车辆的各个部件的平衡位置是符合车辆结构的，最大振幅的基本变化规律也是合理的。

综上所述，轨下高低不平顺主要影响轮对及构架，对车体的影响并不大，因此要减轻车轨系统的振动可以从一系悬挂或者从轮轨接触方面考虑。

参考文献：

[1]龙志强，郝阿明，常文森.考虑轨道周期性不平顺的磁浮列车悬浮控制系统设计[J].国防科技大学学报，2003，025（002）：84-89.

[2]杨航.轮轨力和轨道不平顺识别方法研究[D].北京交通大学，2016.

[3]孙继武，任利惠，王文斌.基于Adams的列车碰撞三维动力学模型和仿真[J].计算机辅助工程，2013，022（004）：51-56.

[4]晋智斌.车—线—桥耦合系统及车—桥随机振动[D].西南交通大学，2007.

[5]郭高杰，向俊，赫丹.套靴刚度和阻尼对高速列车-弹性支承块式无砟轨道系统竖向振动的影响[J].石家庄铁道大学学报（自然科学版），2008（01）：31-33.

[6]杨广军.车辆—无碴轨道—桥梁系统竖向耦合振动特性的研究[D].上海交通大学，2007.

[7]郭高杰.高速列车—弹性支承块式无碴轨道系统竖向振动分析[D].中南大学，2008.

[8]陈果，翟婉明.铁路轨道不平顺随机过程的数值模拟[J].西南交通大学学报，1999.

[9]何越磊，陈施宇，李再帏.基于小波变换的轨道不平顺数值模拟方法[J].城市轨道交通研究，2014，17（010）：59-62.

[10]刘永存，孙立，郜永杰.轮轨系统激励下列车-轨道耦合系统的振动分析[J].铁道勘测与设计，2010，000（005）：22-26.

[11]凌亮.考虑多节车的高速列车/轨道耦合动力学研究[D]. 西南交通大学，2012.

[12]翟婉明.车辆—轨道垂向系统的统一模型及其耦合动力学原理[J].铁道学报，1992，14（3）：10-21.

[13]徐志胜，翟婉明.城市轨道交通支承块式无碴轨道轮轨噪声分析[C]//.中国铁道学会环保委员会噪声振动学组年会.