基于LSTM的混凝土坝变形预测模型

欧 斌,吴邦彬,袁 杰，李淑芳

(1．云南农业大学水利学院，云南 昆明 650201； 2.南昌工程学院，江西 南昌 330099；3.浙江中水工程技术有限公司，浙江 杭州 310000)

混凝土坝作为调节水资源时空优化分布、促进国民经济发展的主要基础设施之一[1-2]，其在运行期不仅长期承受静水荷载、温度荷载等循环荷载的作用，还面临着特大洪水、地震等突发性自然灾害以及战争、恐怖袭击等多重风险威胁，运行环境异常复杂[3-5]。为实时掌握大坝的运行性态，在大坝建设时期就埋设了诸多监测仪器用以监测水位、温度等环境变量与变形、渗流、应力、应变等结构响应[5]。变形作为最直观可靠的反映混凝土坝综合运行性能的重要监测量，结合大坝原型监测资料构建大坝变形与其影响因子之间的数学模型是大坝安全监控领域研究的重点[6-10]，也是有效评估大坝运行安全、预测其未来运行行为的重要科学手段。

根据变形及其影响因子间的数学关系构建的大坝变形预测统计模型因具有函数形式简单、计算高效等优点，在大坝安全监控领域得到了广泛应用[11-13]。逐步回归、多元回归等回归分析方法是实际工程领域最常用的变形预测模型建模方法，然而回归方法不能有效解决影响因子间的多重共线性问题，导致模型预测精度不佳[12,14]。伴随计算机技术的发展，支持向量机(SVM)[9,15-16]、相关向量机(RVM)[17-18]、极限学习机(ELM)[19-20]、人工神经网络(ANN)[21]等多种机器学习算法被广泛应用于变形预测模型，显著提升了监控模型的精度。然而神经网络模型存在过拟合、易陷入局部极值等缺陷。SVM虽一定程度上克服了神经网络模型的缺陷，但其也存在着模型超参数难以选取等不足[18,22-23]。近年来，随着深度学习技术的发展，循环神经网络(RNN)的优势变体长短期记忆网络(long short-term memory， LSTM)在交通、电力等非平稳时间序列预测中取得了广泛应用，并表现出优越的长期与短期预测性能[24-26]，然而其在大坝变形预测中的应用研究[27-29]目前还不是很多。LSTM通过巧妙引入细胞状态(cell state)与门控(gate)概念，有效解决了传统神经网络模型存在的梯度爆炸与梯度消失的通病，并可以合理考量时序样本中前期信息的影响，在合理预测大坝变形中具有显著优势[30]。本文在简述LSTM基本原理的基础上，提出了一种基于LSTM网络的混凝土坝变形预测模型，并结合工程实例对预测模型进行了检验。

1 混凝土坝变形预测原理

根据坝工原理可知，坝体任一点的变形由水压、温度与时效变形3部分组成[31-33]，如式(1)所示。其中，水压变形δH与温度变形δT分别是静水荷载与温度荷载循环作用下引发的可逆变形，对于重力坝，δH可按式(2)计算；对于拱坝，δH可按式(3)计算；对于水化热已完全散发的混凝土坝，坝体混凝土温度随季节变化而变化，故δT常采用谐波函数加以计算，如式(4)所示。时效变形δθ是筑坝材料性能老化与结构损伤等导致大坝安全裕度降低的时变不可逆变形，可由式(5)计算。

δ=α0+δH+δT+δθ

(1)

(2)

(3)

(4)

δθ=c1(θt-θ0)+c2(lnθt-lnθ0)

(5)

式中：α0为常数；αi为回归系数；Ht、H0分别为监测日与建模序列初始日的上游水深；t、t0分别为监测日与建模序列初始日距始测日的累计天数；θt=t/100，θ0=t0/100。

2 基于LSTM的混凝土坝变形预测模型

2.1 LSTM原理

LSTM是一种特殊的RNN，其通过引入细胞状态和门控概念，有效解决了传统RNN所存在的梯度爆炸、梯度消失与长期依赖问题，具有出色的时序预测性能[27,30]。LSTM单元结构主要由细胞状态、遗忘门、输入门和输出门组成[34-35]，如图1所示。细胞状态也称为记忆单元，其类似于传送带，为信息的传递提供通道。细胞状态的更新由遗忘门、输入门与输出门协同控制。

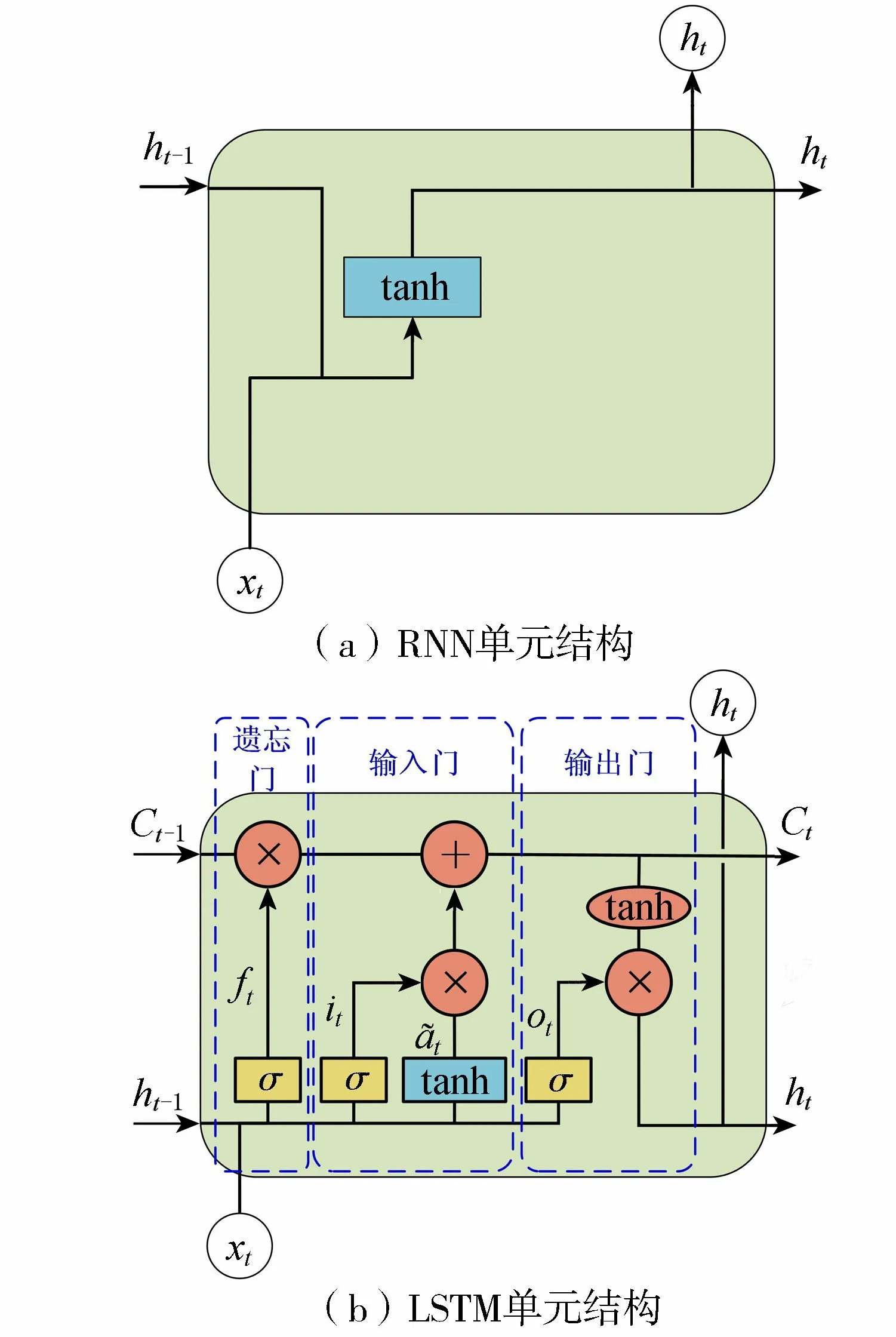
图1 RNN与LSTM单元结构

遗忘门以一定的概率决定是否保留上一时刻的细胞状态以及选择所需保留的信息比重，其读取上一时刻的隐藏层输出ht-1和当前时刻的输入xt，通过一个sigmoid激活函数得到遗忘门的输出ft

ft=σ(Wf·(ht-1,xt)+bf)

(6)

式中：Wf为遗忘门的权重矩阵；bf为偏置项；σ为sigmoid激活函数，σ(x)=1/(1-e-x)；遗忘门的输出ft控制对上一时刻细胞状态信息的遗忘程度，其取值范围为[0,1]，当ft=1时表示完全保留，当ft=0则表示完全遗忘。

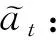
it=σ(Wi·(ht-1,xt)+bi)

(7)

(8)

式中：Wi、Wc分别为sigmoid层和tanh层的权重矩阵；bi、bc分别为sigmoid层和tanh层的偏置项；tanh为双曲正切函数，tanhx=(1-e-x)/(1+e-x)。

基于遗忘门和输入门对上一时刻细胞状态和当前时刻输入的信息的选择，细胞状态可更新为

Ct=ftCt-1+itat

(9)

输出门从当前细胞状态中提取有效信息用以产生新的隐藏层。首先，通过sigmoid函数决定当前细胞状态中的输出部分，然后通过tanh函数对当前细胞状态加以处理，最后生成新的隐含层ht：

ht=ottanhCt

(10)

其中ot=σ(Wo·(ht-1,xt)+bo)

式中：Wo为输出门的权重矩阵；bo为偏置项。

综上可知，LSTM当前时刻的隐藏层输出ht和细胞状态Ct由上一时刻的隐藏层输出ht-1、细胞状态Ct-1与当前时刻的输入xt协同决定。

2.2 LSTM网络结构

在利用LSTM构建回归预测模型时，隐藏层的数量对模型的训练精度和效率有着显著影响。理论上讲，虽LSTM模型的拟合精度会随着隐藏层层数的增加而提高，但过多的隐藏层会导致模型的训练效率降低，甚至造成模型的拟合与预测精度降低。相关研究指出，具有两个隐藏层的LSTM模型即可较好地学习并训练大坝变形与其影响因子间复杂的非线性关系[36]，故本文采用具有2个LSTM隐藏层的网络结构。同时，网络训练中采用dropout技术以避免过拟合，即模型训练效果良好而预测性能欠佳的问题，并利用批处理技术用以提升模型的训练效率[27]。

3 工程案例

3.1 工程背景

我国福建省某混凝土重力坝工程为I等枢纽工程，该坝最大坝高113.0 m，坝顶高程179.0 m。该工程内部布置了3组正、倒垂线监测仪器用以观测该坝坝体与坝顶的水平变形，布置方案如图2所示，图中PL1～PL7为正垂监测点，IP1～IP3为倒垂监测点。

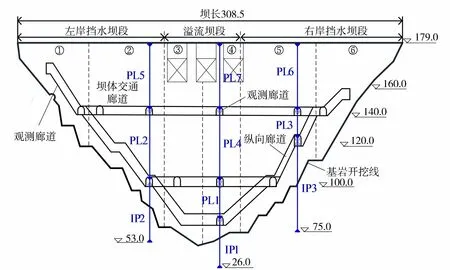
图2 大坝变形监测布置方案(单位：m)

以2006年1月1日至2008年12月31日正垂PL5测点自动化监测得到的左岸挡水坝段坝顶水平变形为例，对所提建模方法进行详细描述，其中，监测序列中后2个月的测值用以预测以检验模型的预测能力。监测时段内库水位与测点水平变形如图3所示，其中负值代表向上游方向变形。由图3可知，随着库水位的上升，左岸挡水坝段坝顶向下游方向的水平变形增大；反之，坝顶向上游方向的水平变形增大，其变形行为符合大坝变形的一般规律。

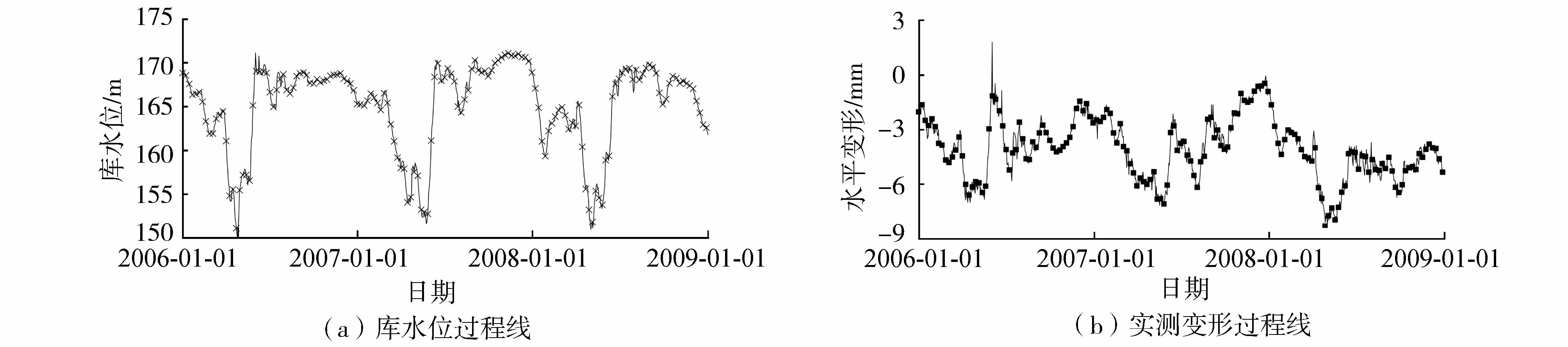
图3 库水位与坝顶水平变形过程线

3.2 建模预测

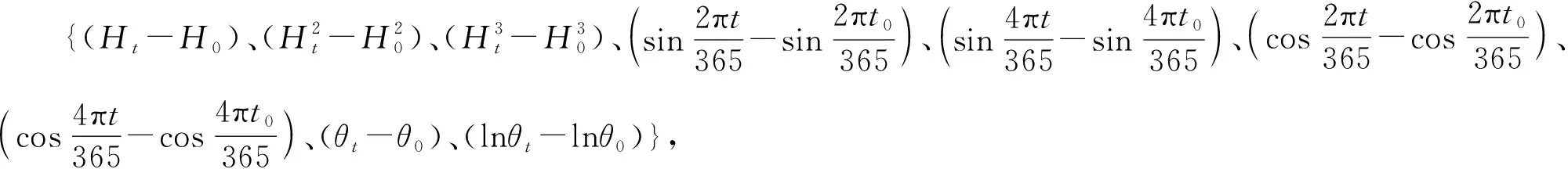
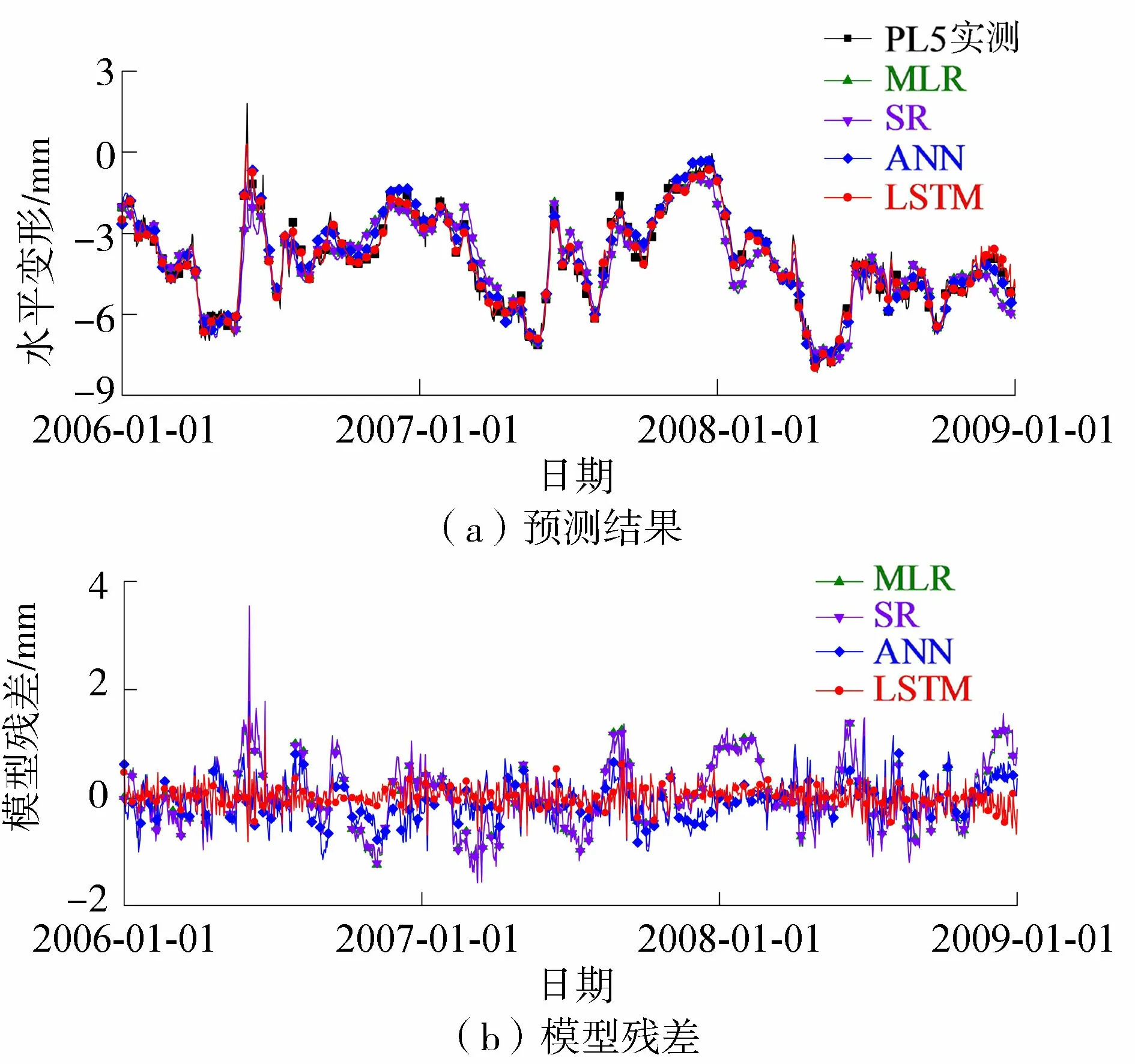
图4 PL5测点预测结果

为验证模型的适用性，同时采用上述4种方法对相同监测时段正垂PL2测点监测的坝体水平变形加以建模预测，预测结果及模型残差如图5所示。此外，为量化对比4种模型的预测精度，表1给出了PL5与PL2测点各模型建模与预测的平均绝对误差(mean absolute error, MAE)、均方误差(mean square error, MSE)与均方根误差(root mean square error, RMSE)。

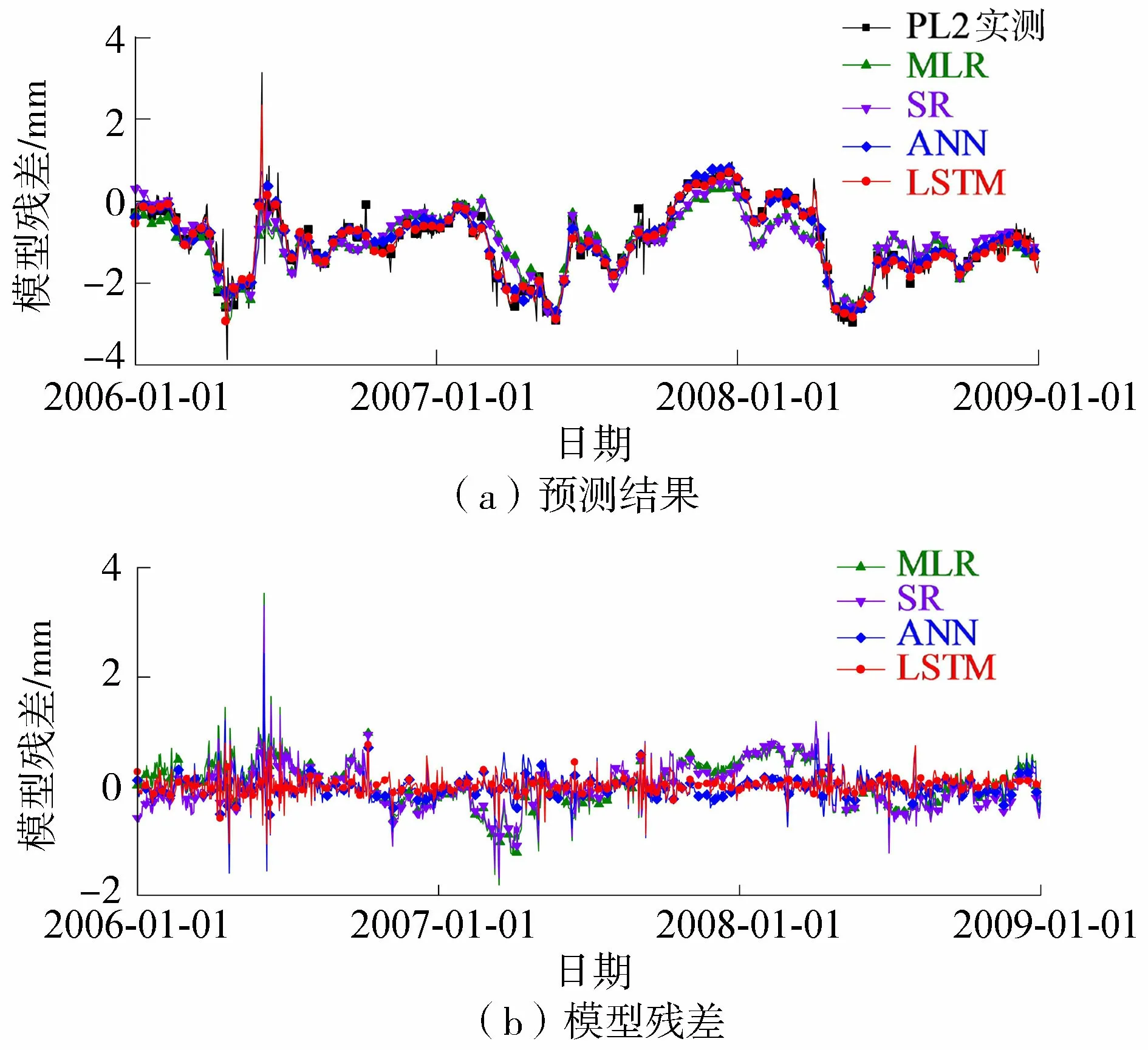
图5 PL2测点预测结果

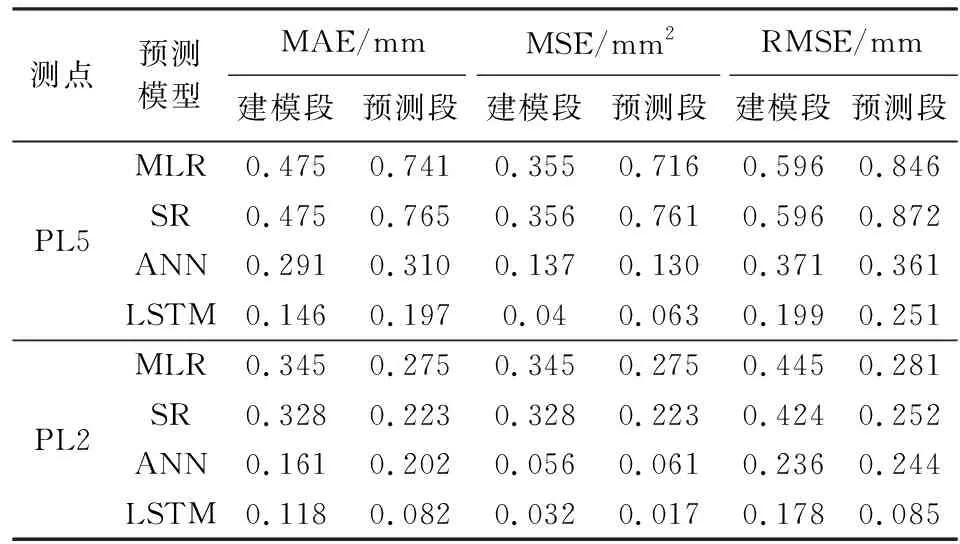
测点预测模型MAE/mmMSE/mm2RMSE/mm建模段预测段建模段预测段建模段预测段PL5PL2MLR0.4750.7410.3550.7160.5960.846SR0.4750.7650.3560.7610.5960.872ANN0.2910.3100.1370.1300.3710.361LSTM0.1460.1970.040.0630.1990.251MLR0.3450.2750.3450.2750.4450.281SR0.3280.2230.3280.2230.4240.252ANN0.1610.2020.0560.0610.2360.244LSTM0.1180.0820.0320.0170.1780.085

根据图4与图5中2个测点水平变形的预测结果可知，基于SR、MLR、ANN与LSTM 4种算法构建的预测模型的建模与预测结果与实测变形测值变化过程基本一致。相比而言，基于LSTM的预测模型比基于SR、MLR、ANN 3种方法的预测模型的建模与预测结果更为接近实测变形，同时其模型残差无明显的变化规律且其变化范围显著较小。由此可知，基于LSTM的预测模型可更好地学习并训练大坝变形与其影响因子间复杂的非线性函数关系，所建变形预测模型的精度更优。此外，由表1中的统计指标可知，基于LSTM所建的两个测点的预测模型在建模与预测段的MAE、MSE与RMSE均相对较小且各自接近，说明所建模型不存在过拟合现象，并进一步表明了所建模型具有出色的建模与预测性能。

4 结 论

a.以LSTM网络为基础构建的混凝土坝变形预测模型具有良好的非线性信息挖掘能力，可有效地挖掘大坝变形及其影响因子间复杂的非线性函数关系，具有出色的建模与预测精度，证明了LSTM网络在大坝变形预报中的可行性和有效性。

b.某混凝土坝实测变形资料建模分析表明，相比于回归模型，基于LSTM网络所建的变形预测模型的预测性能更优，为高精度预测大坝变形提供了一种新技术。且该方法简便高效，加以修改可推广应用于大坝其他监测效应量的预测分析中。