柱形内波观测浮标的设计与稳定性分析

刘 浩陈 亮王火平连伟琪曲志平熊学军

(1.中海石油深海开发有限公司,广东 深圳 518000;2.自然资源部第一海洋研究所,山东 青岛 266061;3.青岛海洋科学与技术试点国家实验室区域海洋动力学与数值模拟功能实验室,山东 青岛 266237;4.自然资源部海洋环境科学与数值模拟重点实验室,山东 青岛 266061;5.青岛科技大学机电工程学院,山东 青岛 266061)

海洋观测浮标是一种可以搭载海洋环境要素观测设备或传感器的稳定平台,具有长期、定点、连续、实时、全天候观测等诸多优势。在海洋观测浮标技术发展初期,大多采用的是直径不小于8 m 的大型浮标。例如,20世纪中期美国建造的浮标网,其浮标直径均为10～12 m;1978年10月,中国正式投入使用的HFB-1A 型浮标,其直径为10 m[1]。这是因为浮标的尺寸越大,其稳定性越好[1]。大型浮标虽然稳定性好,但其建造成本高,布放、维护和回收的难度较大。因此,随着CMOS微处理机技术的进步和卫星通信技术在海洋设备上的应用以及材料工艺的发展,浮标越来越趋向于小型化[2]。

按照海洋观测浮标的结构形式,可以将其分为圆盘形、球形、船形和柱形等[3-4]。其中柱形浮体或准柱形浮标在海洋观测中应用最为广泛,其优点在于吃水线深、稳定性好、不易倾覆、造价低等[4]。在内波观测和预警应用中,海流及温盐剖面的现场观测数据需要通过海面浮标实时传输回陆地基站或应用平台。海流剖面观测数据的实时传输目前主要有2种方式:第一种是采用观测设备与海面标体分离的方式,即将海流剖面观测仪(如声学多普勒流速剖面仪,Acoustic Doppler Current Profilers,ADCP)安装于水下主浮体内,通过传输缆或其他通讯方式将采集的数据传输至海面标体,再通过安装在海面标体上的天线经卫星实时传输回基站;第二种是将海流观测设备与海面通进而讯装置均安装在海面浮标上[5],这种方式避免了数据采集传输至海面信标的中间过程,更为简单直接,降低了数据传输出现故障的可能性。

在第二种方式中,由于海流观测设备直接安装在海面标体上,其姿态必然会受到海面波浪的影响。以ADCP为例,当其横摇(Pitch)或纵摇(Roll)倾角超过20°时,观测数据将会失效。因此,有必要针对在海面波浪影响下的观测浮标的倾角问题进行研究。本文将以柱形观测浮标为例,讨论在标准波浪影响下浮标的姿态变化,并给出小型化柱形观测浮标合理的设计尺寸。

1 浮标设计和模拟方法

本文针对美国RDI公司生产的RDI 75k ADCP,设计了一种包裹式圆柱形内波观测浮标(以下简称柱形观测浮标)(图1a),其内径比75k ADCP舱体直径大1 cm,可确保75k ADCP舱体刚好安装于柱形观测浮标内。浮体选用空心玻璃微珠与环氧树脂饱和混合加温固化成型的复合型浮体材料,其密度为450 kg/m3。在后续计算和模拟过程中,对ADCP的换能器头部进行了简化,将其近似为直径40 cm 、厚度10 cm 的圆饼形。图1b为圆柱形观测浮标模型的二维图,本文探讨了控制浮体直径D(或高度H)不变、在标准波浪(浪高1 m)的影响下,不同高度H(直径D)浮体的姿态(横摇和纵摇)变化情况。本文采用Solid Works软件[6]对不同尺寸参数的该型浮标进行建模,采用ANSYS Workbench 2020软件[7]中的AQWA 模块对该型浮标进行网格划分和姿态模拟。

图1 包裹式图柱形内波观测浮标模型Fig.1 Model of the package-type cylindrical inner wave observation buoy

1.1 AQWA软件理论基础

基于AQWA 软件的三维势流理论基本假设,假设流体中的流速场(φ)是标量函数梯度的流,是无旋、无黏、不可压缩的理想流体,满足以下的边界条件[7]:

式中:n为法线方向的变量;v j为浮体在(x,y,z)点的方向速度;f j为(x,y,z)点的有限微元的面积。

5)辐射条件:

AQWA 软件中的参考坐标系Oxyz坐标原点在水平面上,Oxy平面与水面重合,z轴垂直于水面向上,模型在坐标系中位置如图1b所示。

利用ANSYS Workbench 2020的Hydrodynamic Diffraction模块进行频域计算,计算在去向与x轴间的夹角为90°、周期在1～20 s范围内的波浪作用下,柱形观测浮标的横摇倾角大小,通过对比寻找最优的模型参数解。

1.2 三维建模与参数设置

改变柱形观测浮标的形状尺寸参数,记录下不同形状尺寸模型的质量、质心坐标,并计算模型的吃水线(ζ)、转动惯量等参数,导入ANSYS Workbench 2020的Hydrodynamic Diffraction模块中进行频域分析。

柱形观测浮标观测海域在南海北部陆坡区,因此全局变量参数设置如下:水深300 m,水域模型为边长100 m 的正方形海域,海水密度1 025 kg/m3,重力加速度9.8 m/s2,计算波浪周期1～20 s,波浪振幅1 m。质量参数根据在Solid Works软件中记录的不同尺寸浮体参数进行设置。

1.3 网格划分

利用AQWA 软件,根据柱形观测浮标尺寸大小进行自动网格划分,定义网格单元的最大尺寸为0.05 m,得到浮体的网格划分如图2所示。

图2 柱形观测浮标的网格划分Fig.2 Grid division of the cylindrical buoy

保持外界的环境载荷条件相同,利用ANSYS Workbench 2020软件的AQWA 模块进行水动力计算,分析柱形浮标在不同直径、不同高度情况下的横摇运动响应。通过对比不同尺寸浮标的横摇幅值响应因子(Response Amplitude Operators,RAO)的差异,可以得出稳定性最好的浮标尺寸,确定小型化柱形观测浮标的最优设计尺寸。

本文在确保浮力足够的情况下,设计了48种不同尺寸的柱形浮标,来分析比较在外界载荷相同的情况下,不同外形参数浮标的横摇响应RAO。各种尺寸浮标的吃水线计算结果如表1所示。

表1 不同直径和高度柱形观测浮标的吃水线(m)Table 1 Draft lines of the buoys with different diameters and heights(m)

2 结果分析

2.1 浮体直径变化对柱形观测浮标横摇的影响

图3为限定浮体高度不变,在1～20 s周期的波浪影响下不同浮体直径的柱形浮标横摇倾角变化情况。从图3可见,当浮体高度为1.3 m 时,在保证浮体浮力足够的情况下,无论浮体的直径如何变化,柱形观测浮标横摇角度在波浪周期为1～20 s时均不超过20°;当浮体高度为1.0 m,且浮体直径在0.6 m 以下时,其横摇倾角在波浪周期为9～10 s时会超过20°,最大可达41°;当浮体高度为1.1、1.2、1.4和1.5 m,浮体直径在0.5 m 以下时,其横摇倾角在波浪周期为4～10 s时均有可能超过20°(对不同高度柱形浮标,其横摇倾角超过20°对应的波浪周期有所不同);当浮体高度为1.4 m 和1.5 m 时,最大横摇角度甚至会超过90°,这与柱形观测浮标固有频率与波浪频率一致、二者发生共振有关[8]。此外,由图3还可见,在高频(周期小于5 s)波浪影响下,当浮体直径大于0.8 m 时,其横摇角度明显比直径为0.6～0.7 m 时大。由此可见,在高频波浪的影响下,并非直径越大,柱形观测浮标越稳定。

图3 浮体直径变化对柱形观测浮标柱形观测横摇的影响Fig.3 Influence of the change of floating body diameter on the roll of the cylindrical buoy

2.2 浮体高度变化对柱形观测浮标横摇的影响

图4为限定浮体直径不变,在1～20 s周期的波浪影响下不同浮体高度的柱形浮标横摇倾角变化情况。由图4可见,当浮体直径为0.4 m 时,几乎各种高度的浮体样本(H=1.3 m 除外)在波浪周期低于10 s时,均出现了横摇角度超过20°的情况;当浮体直径为0.5 m 、高度为1 m 时,在周期为9～10 s的波浪影响下,同样出现了横摇角度超过20°的情况;而当直径不小于0.6 m 时,其在周期为1～20 s的波浪影响下,波浪横摇角度均不超过20°。但当浮体直径为0.7 m 时,柱形观测浮标最为稳定。由此可见,在高频波浪的影响下,并非直径越大,浮标越稳定。

图4 浮体高度变化对柱形观测浮标横摇的影响Fig.4 Influence of the change of floating body height on the roll of the cylindrical buoy

2.3 柱形观测浮标尺寸的选取

通过分析可知,在波浪周期为1～20 s范围内、浮体直径一定的前提下,浮体的高度为1.3 m 时姿态最稳定,横摇角度没有出现极端的数值结果,且总体横摇较小;浮体高度一定的前提下,柱形观测浮标的直径在0.7 m 时姿态最稳定。当浮体高度为1.3 m 时(图5a),不同浮体直径对柱形观测浮标稳定性的影响。从图5可见,当浮体直径为0.6和0.7 m 时,柱形观测浮标相对最稳定,其横摇角度在周期为1～20 s的波浪作用下均小于10°;当浮体为其他直径时,在高频波浪影响下,柱形观测浮标横摇角度有可能会超过10°。图5b展示了浮体直径为0.7 m 时,不同浮体高度对柱形观测浮标稳定性的影响。从图5b可见,在浮体直径为0.7 m时,浮体高度对柱形观测浮标的稳定性影响差别较小,其横摇角度均能控制在10°以内。而当浮体高度为1.2和1.3 m 时,在高频波浪影响下,横摇角度相对更小,表现为最稳定。

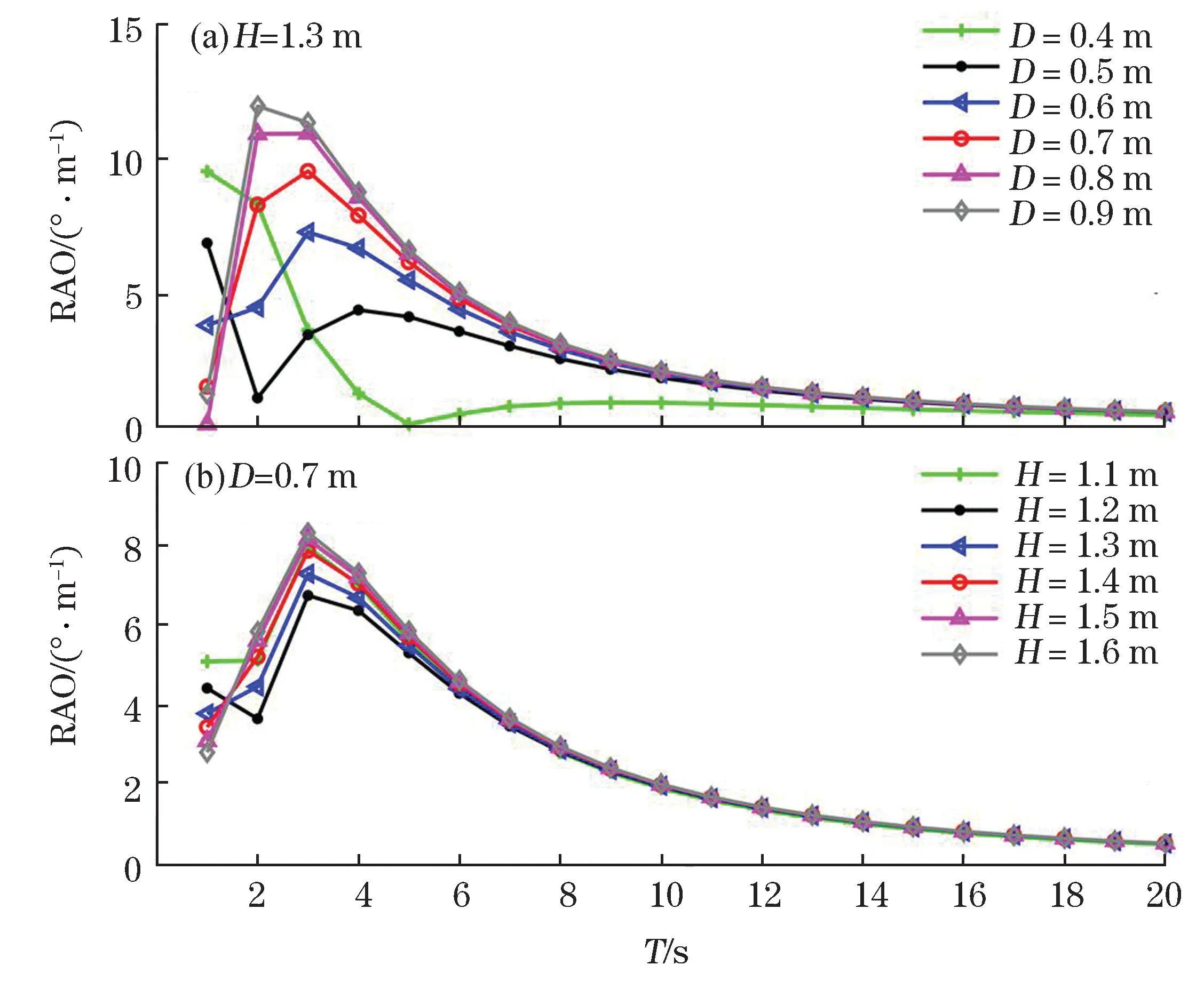
图5 不同周期波浪影响下的柱形浮标横摇角度变化曲线Fig.5 Changes of the roll angle of the cylindrical buoy under the influence of the waves with different periods

3 结 论

随着浮标观测技术的发展,海面浮标越来越趋向于小型化,本文针对所设计的48种不同尺寸的柱形观测浮标,采用Solid Works软件和ANSYS Workbench 2020软件,分析比较了在外界载荷相同的情况下,不同外形参数柱形观测浮标的横摇变化情况。分析结果表明:

1)当浮体高度为1.3 m 时,在保证浮体浮力足够的情况下,对于各种本直径的柱形观测浮标,在周期为1～20 s的波浪影响下,其横摇角度均可不超过20°;当浮体高度为1.1、1.2、1.4和1.5 m,浮体直径在0.5 m以下时,其横摇角度在波浪周期为4～10 s时均有可能超过20°(不同浮体高度,横摇角度超过20°对应的波浪周期有所不同);当浮体高度为1.4和1.5 m 时,最大横摇角度甚至会超过90°,这与柱形观测浮标固有频率与波浪频率发生共振有关[8]。因此,对于小型柱形观测浮标的设计,需要特别注意避免高频波浪与浮标固有频率的共振问题。

2)当浮体直径不小于0.6 m 时,对于所有浮体样本高度,其横摇角度在周期为1～20 s的波浪作用下均不超过20°;当浮体直径为0.7 m 时,柱形观测浮标最为稳定,其横摇角度最大不超过10°。在高频(周期小于5 s)波浪影响下,当浮体直径大于0.8 m 时,其横摇角度明显比直径为0.6～0.7 m 时大。由此可见,在高频波浪的影响下,并非直径越大,柱形观测浮标越稳定。

3)对于所讨论的48种不同尺寸的柱形观测浮标,浮体高度为1.2～1.3 m、浮体直径为0.6～0.7 m 时,柱形观测浮标最为稳定。

本文系统性地讨论了小型柱形观测浮标不同设计尺寸对其姿态的影响,并给出了最优化设计尺寸,这对于小型浮标设计和表面浮标观测剖面流具有重要的参考意义。