基于特高含水期相渗规律的含水率预测新模型

曲 江，夏连晶

大庆油田有限责任公司第四采油厂，黑龙江 大庆

1. 引言

对于水驱开发油田，含水率是反映油田含水上升规律的重要指标，是评价水驱油田开发效果、分析油田生产动态的重要指标。历年来国内外学者对含水上升规律进行深入研究，目前常用的含水率预测方法[1] [2] [3] [4] [5]主要包括Gompertz 模型、Logistic 模型和Usher 模型，这三种方法通常反映了含水率与时间的统计规律，缺乏理论依据，当含水率出现剧烈波动时，该方法适用性差；而常用的水驱规律曲线[6] [7] [8] [9]虽能反映油水渗流理论，但进入特高含水期后油水相对渗透率比值与含水饱和度在半对数曲线上偏离直线关系，不能用于特高含水期含水率预测。因此，本文基于特高含水期相渗规律，建立了一种反映含水率与采出程度关系的含水率预测新方法，既能反映特高含水期油水渗流规律，又能提高特高含水期含水率预测精度，为特高含水期水驱油藏开发规划制定提供了理论依据。

2. 目前含水率预测模型

目前常用的含水率预测方法主要包括Gompertz 模型、Logistic 模型和Usher 模型，这三种方法均反映了含水率与时间的统计规律。

2.1. Gompertz 模型

英国统计学家和数学家冈珀茨Gompertz 于1825 年提出了一种预测动物种群生长模型，使用该模型能够描述种群的消亡规律和比较植物病害进展曲线。后来将这种广泛用于经济增长和油气资源增长预测的Gompertz 模型[10]应用于水驱开发含水率预测中，其一般形式为

式中：fw为油田含水率，%；t为油田开发时间，a；k、b为拟合系数。

将公式(1)变形，得到lnfw与t之间的关系，见公式(2)，通过公式拟合即可得到拟合系数k和b的数值。

2.2. Logistic 模型

Logistic 模型[11]又称Logistic 回归分析，该模型在流行病学中应用较多，能够根据危险因素预测某疾病发生的概率。美国地质学家哈伯特King Hubbert 于1962 年提出将Logistic 模型应用于油田开发指标预测中，其一般形式为

将公式(3)变形，得到1/fw- 1 与t之间的关系，见公式(4)，通过公式拟合即可得到拟合系数k和b的数值。

2.3. Usher 模型

美国学者Usher 于1980 年提出了一种增长数据随时间变化数学模型。将该模型应用于水驱开发油田，发现当t→∞时，fw→ 1，即预测含水率Usher 模型[12] [13]的一般形式为

式中：c为拟合系数。

将公式(5)变形，得到fw与t之间的关系，见公式(6)，应用试凑法，通过改变拟合系数c获得最大的相关系数，即可得到拟合系数k和b的数值。

从以上表达式可以看出，用于含水率预测的Gompertz 模型和Logistic 模型是Usher 的两种简化形式，当c= 0 时，对公式(5)求导可得到Gompertz 模型，当c= 1 时，直接得到Logistic 模型。Gompertz模型和Logistic 模型曲线呈“S”形状，曲线中存在一个最大增长速度——拐点，Gompertz 模型拐点发生在NR/e 处，Logistic 模型拐点发生在NR/2 处，这说明上述两个模型的拐点位置只与可采储量有关，不适用于含水率拐点位置不符合相关规律的油藏。而Usher 模型为三参数(k、b和c)模型，引入了参数b，拐点的位置与参数b和可采储量有关，提高了Usher 模型的适用范围，与Gompertz 模型和Logistic 模型相比具有同等或更高的预测精度。

这三种模型均反映了含水率与时间的统计规律，用于油田含水率预测时缺乏理论依据、各参数无实际物理意义。当油田进入稳定递减阶段后，含水率变化随开发时间呈稳定变化趋势；当油田进行大规模井网加密或重大措施调整时，产油量曲线剧烈波动，含水率出现明显的降低或太高趋势，上述方法适用性变差。

3. 特高含水期相渗规律

油水相对渗透率曲线是研究油水两相渗流的基础，是油田开发指标计算、动态分析等方面不可缺少的重要资料，能够反映水驱油藏油水渗流规律。图1(a)为任一复合相渗曲线，当进入油水渗流阶段后，水相相对渗透率与油相相对渗透率比值krw/kro与含水饱和度之间半对数直线关系；当含水率超过90%后，进入特高含水阶段，此时两者偏离直线关系出现明显上翘，如图1(b)所示，因此需要建立新的特高含水阶段油水渗流理论。

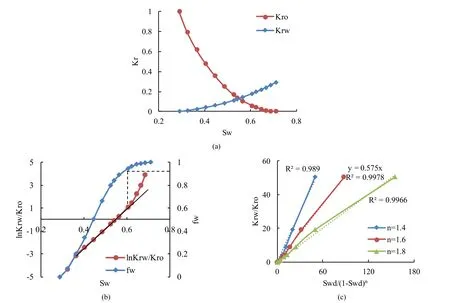
Figure 1. Law of oil-water relative permeability curve. (a) Relative permeability curve; (b) Relative permeability curve law in steady seepage stage; (c) Relative permeability curve law in extra-high water cut stage图1. 油水相对渗透率曲线规律。(a) 相对渗透率曲线；(b) 稳定渗流阶段相渗规律；(c) 特高含水期相渗规律

通过深入研究特高含水期相渗曲线变化规律，发现油水相对渗透率比值krw/kro与归一化含水饱和度Swd存在以下关系：

其中

式中：krw、kro为水相相对渗透率、油相相对渗透率；Sw、Swd为含水饱和度、归一化含水饱和度；Swc、Sor为束缚水饱和度、残余油饱和度；b、n为拟合系数。

应用试凑法，通过改变系数n获得最大的相关系数，即可得到拟合系数b的数值。当n= 2 时，油水相对渗透率比值krw/kro与归一化含水饱和度项Swd(1-Swd)n呈明显的直线关系，相关系数无限趋近于1，如图1(c)所示。即公式(7)可以描述油田开发各个阶段油水相对渗透率比值与归一化含水饱和度的关系，不用再区分低含水阶段、中含水阶段、高含水阶段和特高含水阶段。当公式中含水饱和度趋近于束缚水饱和度时，即Swd= 0 时，krw= 0；当含水饱和度趋近于最大含水饱和度时，即Swd→ 1时，k rwkro→∞，这与水驱规律相一致。

4. 特高含水期含水率预测新模型

根据特高含水期相渗曲线变化规律，建立新的特高含水期含水率预测新模型，直接反映含水率与采出程度之间的关系。与已有模型[14] [15]仅能预测高含水阶段的开发指标相比，该模型适用于油气田整个开发过程的含水率预测，含水率预测精度明显提高。

已知采出程度R和驱油效率Ed计算公式，整理公式(8)，当R→ 0时，Swd→ 0，当R→Ed时，Swd→ 1。

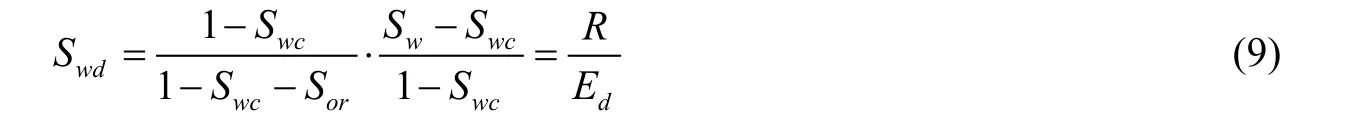
根据油水渗流公式可计算含水率：

将公式(7)和公式(9)代入公式(10)：

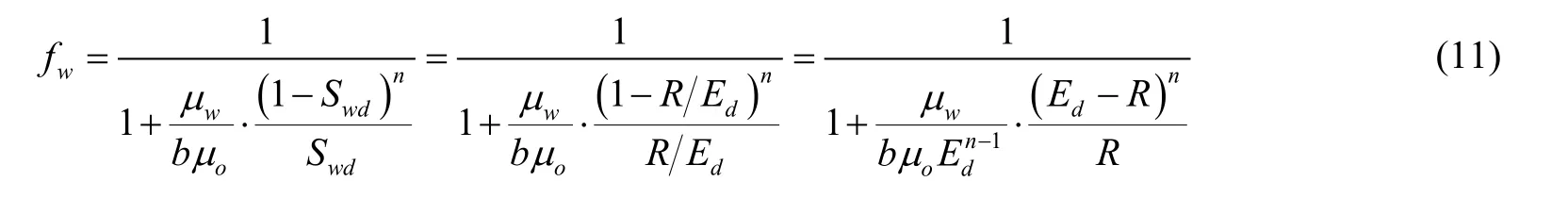
公式(11)整理得：

其中

一般来说，对于某一研究区驱油效率Ed可以通过岩心室内驱油实验获得，根据公式(12)，已知历年开发数据，绘制(1/fw- 1)R与Ed-R之间的关系，确定二者幂函数关系的拟合系数m和n。整理公式(11)，将拟合系数代入公式(14)即可根据采出程度预测未来含水率变化趋势。

5. 实例应用

以大庆油田某一已进入特高含水期的区块为研究对象，1971～2020 年该区块历年开发数据见表1，应用上述4 种方法对1971～2015 年开发数据进行拟合，并预测2016～2020 年含水率，拟合和预测结果如图2 所示。通过拟合分别获得Gompertz 模型、Logistic 模型、Usher 模型和含水率预测新模型的拟合系数k、b、c、m和n的数值，从拟合相关系数来看，拟合精度依次提高，分别为0.6397、0.863、0.8941 和0.9416。

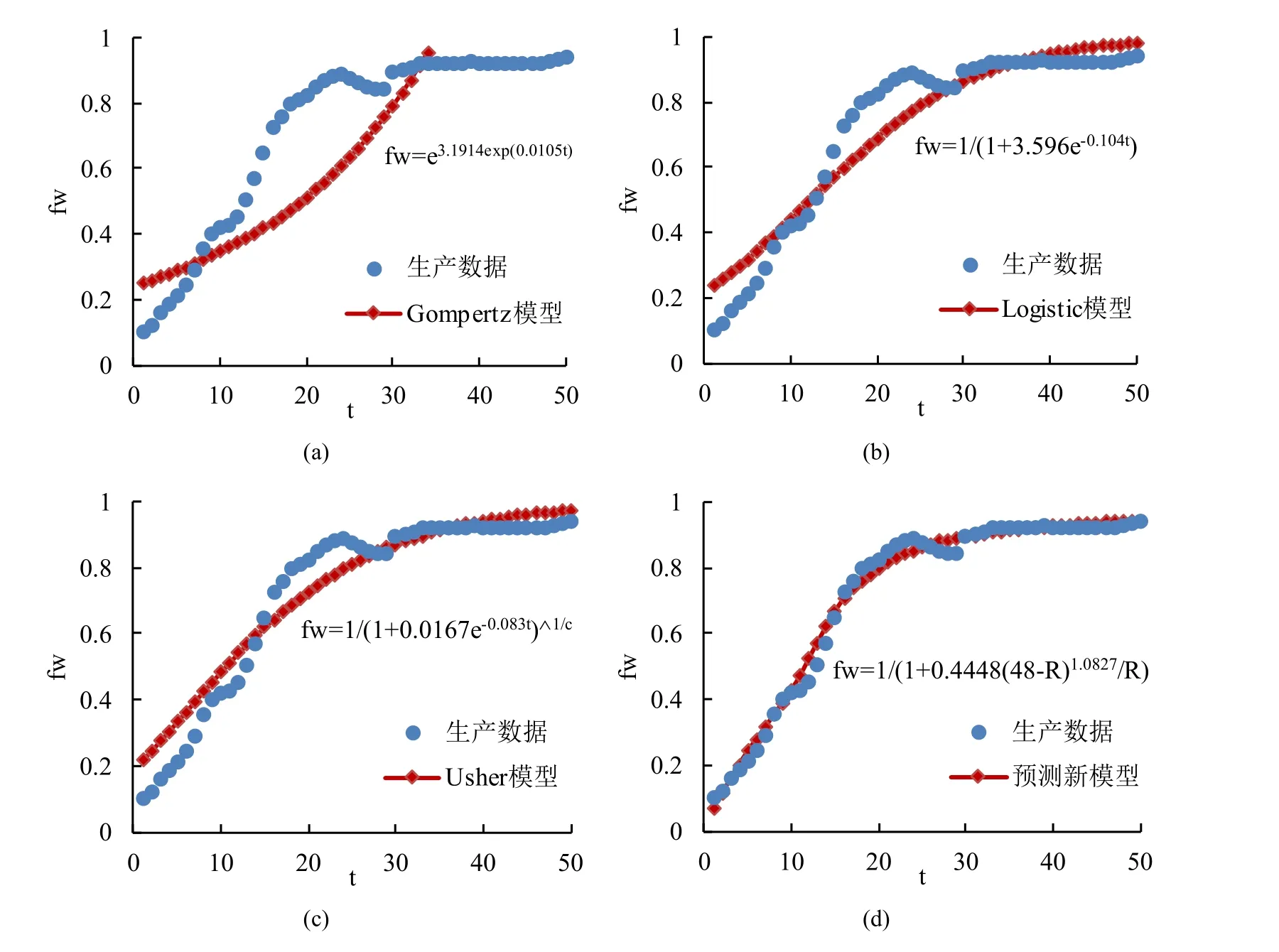
Figure 2. Water cut prediction results of each method. (a) Goempertz model; (b) Logistic model; (c) Usher model; (d) A new prediction model of water cut图2. 各方法含水率预测结果。(a) Goempertz 模型；(b) Logistic 模型；(c) Usher 模型；(d) 含水率预测新模型

Table 1. Water cut prediction results of each method表1. 各方法含水率预测结果

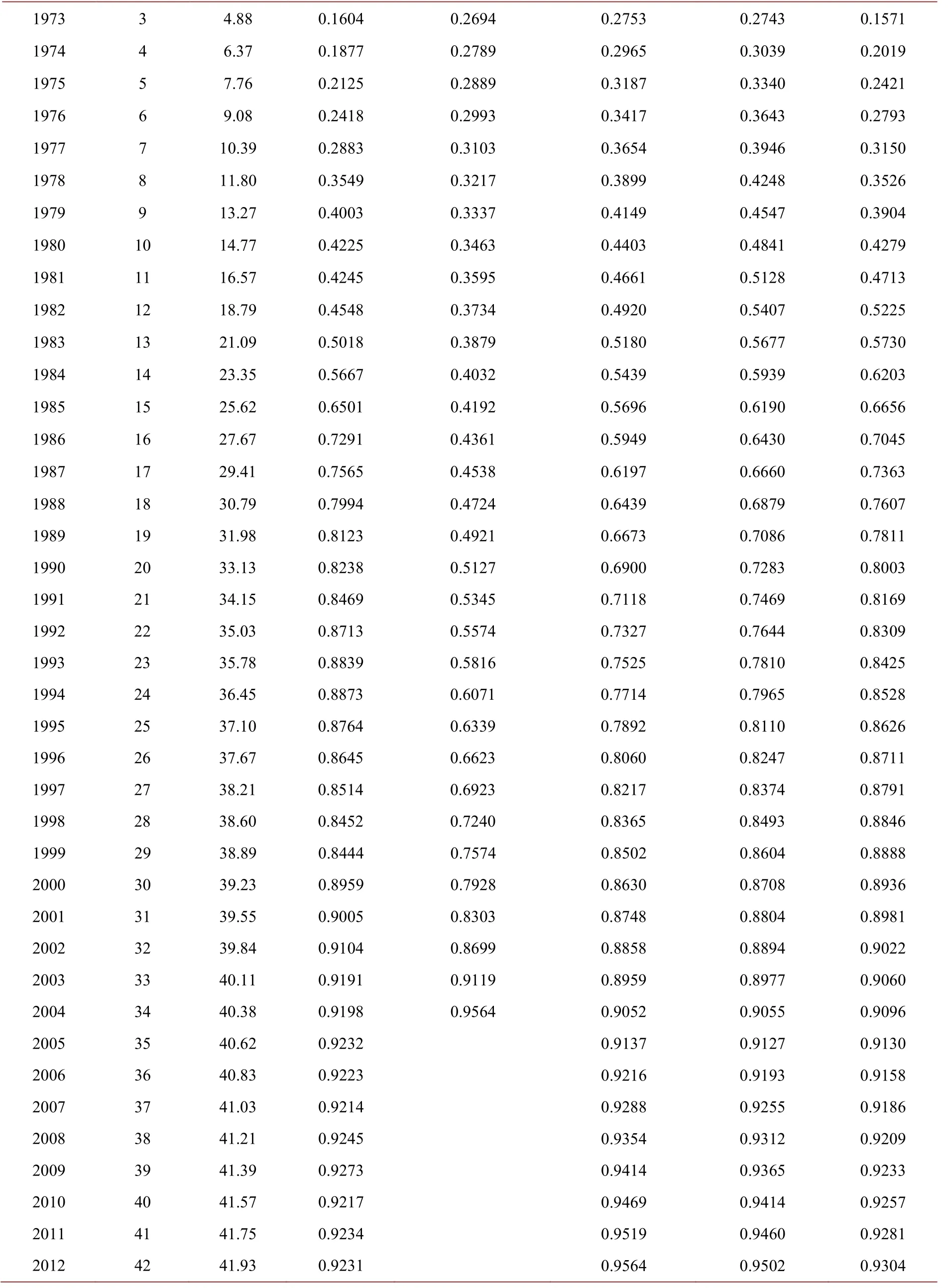
Continued

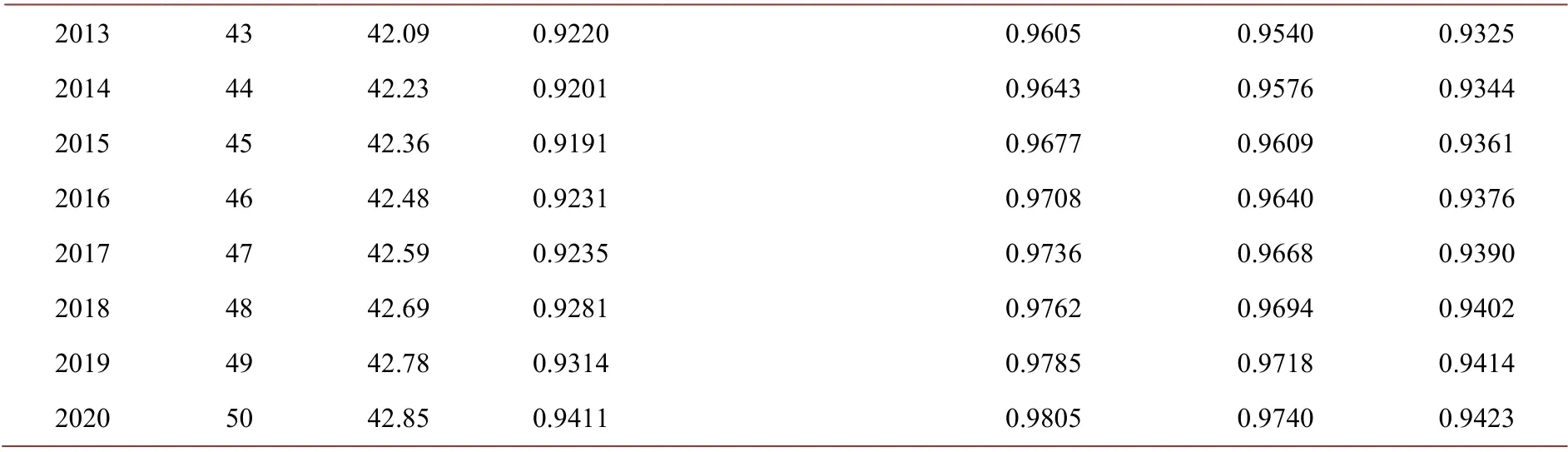
Continued

根据拟合系数，计算2005 年后Gompertz 模型预测含水率超过1；应用Logistic 模型、Usher 模型和含水率预测新模型计算2016～2020 年含水率预测误差分别为5.00%、4.28%和1.15%。通过对于拟合和预测结果可知，与Gompertz 模型、Logistic 模型和Usher 模型相比，含水率预测新模型拟合误差最小，预测精度最高，整体预测效果最好。在整个含水阶段，Gompertz 模型、Logistic 模型和Usher 模型预测含水率均呈逐年上升的趋势，但拟合精度并不高，尤其是进入特高含水期后，含水率预测值明显高于实际数值，与实际不符；而含水率预测新方法在低含水期预测含水率高、特高含水期预测含水率低，最接近于实际含水率数值，可靠性高。

6. 结论

1) 目前常用的含水率预测方法仅反映了含水率与时间的统计规律，缺乏油水渗流理论，而水驱规律曲线虽有理论职称，但特高含水期后油水相对渗透率比值与含水饱和度在半对数曲线上偏离直线关系，不能用于特高含水期含水率预测。

2) 基于特高含水期相渗渗流特征，建立了反映含水率和采出程度变化规律的含水率预测新模型，模型参数求取简单、可靠性高，研究表明与Logistic 模型、Usher 模型相比，含水率预测精度分别提高了3.85个百分点和3.13 个百分点。