一类非局部问题解的存在性

刘丽娟

(太原师范学院数学系，山西 晋中 030619)

1 引言和主要结果

近年来，如下非局部问题被广泛研究:

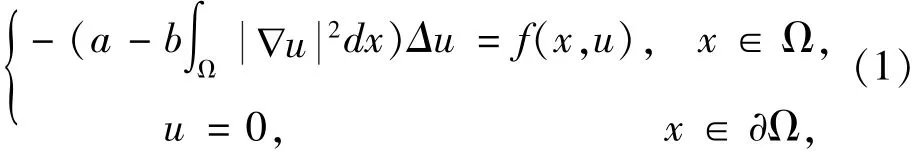
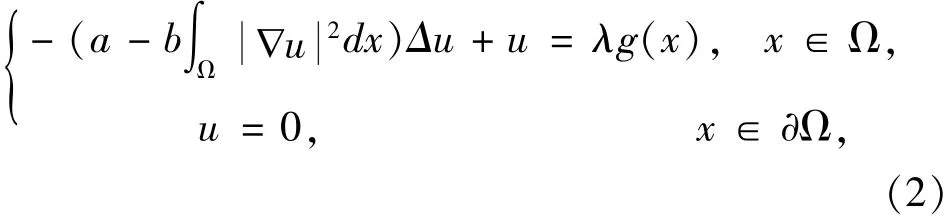
其中Ω⊂ℝ3是有界开集，a＞0，b＞0，λ＞0，g(x)＞0且并得到以下主要结果:

定理1 若a＞0，b＞0，λ＞0，g(x)＞0且则存在Λ＞0，使得任给λ∈(0，Λ)，则问题(2)至少存在一个解.

2 预备知识

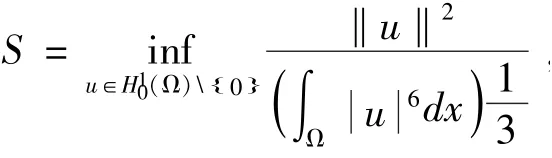
定义Iλ(u)为问题(2)对应的能量泛函，即

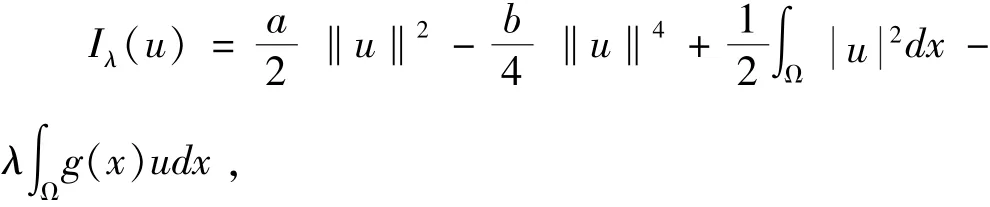
如果u满足

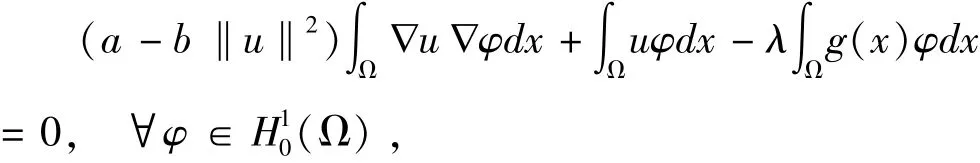
引理1 若常数a＞0，b＞0，λ＞0，g(x)＞0且则泛函Iλ(u)

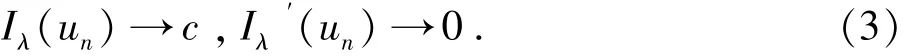
假设{un}无界，则存在{un}的子列，不失一般性仍记为{un}，使得‖un‖→∞，(n→∞)，

由于Iλ(un)→c，得矛盾.由此可知，{un}有界，因此存在满足

由式(4)、(8)可得‖un-u0‖→0，即un→u0，因此Iλ(u)在中满足(PS)条件.

3 定理1的主要证明

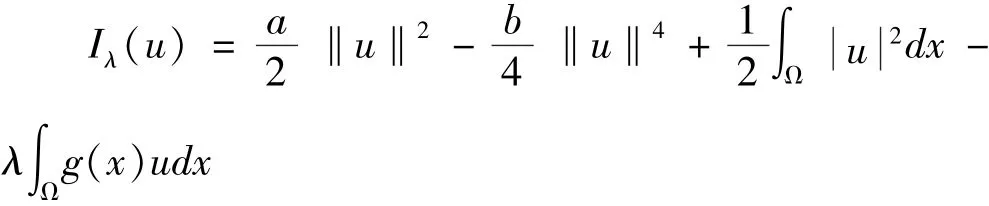
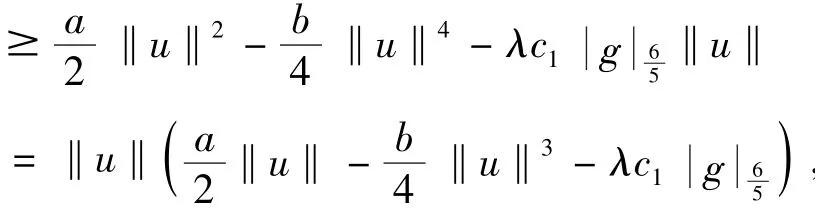
其中c1是与u无关的常数.

其中c2是与u无关的常数.因此当τ→＋∞，Iλ(u)→-∞，所以存在τ1＞0，

满足u1＝τ1u∈H10(Ω)， ‖u1‖＞r，Iλ(u1)＜0，根据山路引理[16]可知存在{un}⊂H10(Ω)，

满足

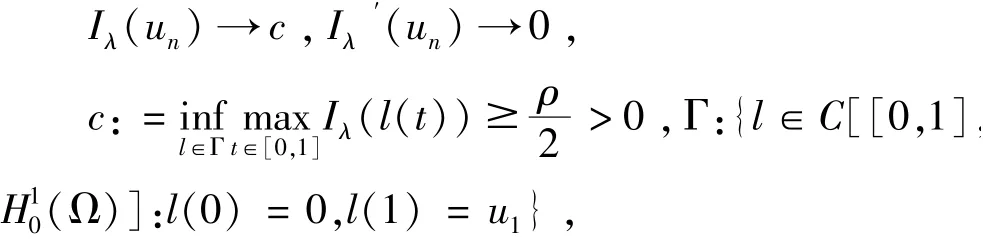
由引理1可知{un}有一个收敛的子列，因此存在使得在中，

un→uλ.由此可得问题(2)至少存在一个解uλ.

4 总结

本文主要考虑了一类形如(2)中带线性项u与参数λ的非局部问题，通过证得能量泛函Iλ(u)满足(PS)条件且当λ∈(0，Λ)时，Iλ(u)具有山路引理的几何结构，证明了问题(2)至少存在一个解，后续可以继续研究该问题解的多重性.