交换环上的n-w-余纯投射模
李 庆
(西南民族大学数学学院,四川 成都 610041)
1 引言及准备知识
本文恒设R为具有单位元的交换环.Enoch和Jenda在文献[1-2]中引入余纯内射模和余纯平坦模.所谓R-模M是余纯内射模[1],是指对任意内射R-模E,所谓R-模M是强余纯内射模[1],是指对任意内射R-模E和任意正整数=0.R-模N称为余纯平坦模[2],是指对任意内射R-模E,模N称为强余纯平坦模[2],是指对任意内射R-模E和任意正整数i≥1E)=0.我们知道平坦模的右正交类是余挠模,而余挠模在刻画环的结构等方面起着重要的作用.类似,平坦模的左正交类成为众多代数学者思考的研究对象,于是Fu等人在文献[3]中引入了n-余纯投射模和强余纯投射模.这里设fdR(F)表示R-模F的平坦维数.所谓M称为n-余纯投射R-模[3],是指对任意fdR(F)≤1的R-模F,称R-模M是强余纯投射模[3],是指对任意平坦R-模F和任意正整数F)=0.随后Gao在文献[4]中进一步刻画了n-余纯投射R-模.在文献[5]中Glaz和Vasconcelos引入了半v-模(semi-divisorial module),推广了v-模(divisorial module)和内射模,随后Vasconcelos修正了半v-模,引入了w-闭包,也就是所谓的w-算子,该算子在乘法理想理论和模论研究中起到了重要的作用,特别是在平坦模类中w-算子的引入产生了许多漂亮的结果,比如文献[6-10].
以下恒设n是非负整数,w-ζn表示w-平坦维数不超过n的所有R-模类.R的极大w-理想的集合记为w-Max(R).
本文研究的目的是在n-余纯投射R-模和强余纯投射模中引入w-算子,提出n-w-余纯投射模和(强)w-余纯投射模的概念以及相关性质刻画.本文讨论了n-w-余纯投射模和强w-余纯投射模在扩张之下的封闭性问题.证明了若R-模正合列0→A→B→C→0,其中A,C都是n-w-余纯投射模,则B也是n-w-余纯投射模.证明了若R-模正合列0→A→B→C→0,其中A,C都是强w-余纯投射模,则B也是强w-余纯投射模.最后分别给出了n-w-余纯投射模和w-余纯投射模的等价刻画.证明了M是n-w-余纯投射R-模当且仅当对任意R-模正合列0→K→K‘→M→0,其中K‘是n-w-余纯投射R-模,则对任意N∈w-ζn,诱导序列0→HomR(M,N)→HomR(K‘,N)→HomR(K,N)→0是w-正合列;当且仅当对任意R-模正合列0→A→B→C→0,其中A∈w-ζn,则诱导序列0→HomR(M,A)→HomR(M,B)→HomRM,C)→0是w-正合列.
下面回顾一些本文常用定义和结果.假设J是交换环R的理想,由文献[11],J称为GV-理想,是指J是R的有限生成理想,且自然同态中φ:R→HomR(J,R)是同构的.GV(R)代表R中所有GV-理想.设R-模M,记torGV(M)={x∈M|Jx=0对某J∈GV(R)}.若torGV(M)=M,称M为GV-挠模;若torGV(M)=0,称M为GV-无挠模.GV-无挠R-模M称为w-模,是指对任意J∈GV(R)有Ext1R(R/J,M)=0.设f:M→N是R-模同态,若对R的任意极大w-理想m,fm:Mm→Nm是单同态(满同态或同构),则称f为w-单同态(w-满同态或w-同构).R-模同态序列A→B→C称为w-正合列,是指对R的任意极大w-理想m诱导的R-模同态序列Am→Bm→Cm是正合列.由[12,命题1.1],R-模同态序列是w-正合列当且仅当f:A→B是w-单同态当且仅当ker(f)是GV-挠模;R-模同态序列是w-正合列当且仅当g:B→C是w-满同态当且仅当cok(g)=C/Im(g)是GV-挠模.由文献[13,定理2.7],R-模M是GV-挠模当且仅当对R的任意极大w-理想m,Mm=0.本文涉及的其他概念等,参见文献[14-16].
2 n-w-余纯投射模
定义2.1R-模M称为n-w-余纯投射,是指对任意是GV-挠模,若n=0,我们称M为w-余纯投射R-模.R-模M称为强w-余纯投射,是指对任意w-平坦模N和所有整数i≥1,是GV-挠模
命题2.2 设R为任意交换环,P是有限生成投射R-模.若R-模M是n-w-余纯投射,则HomR(P,M)和P⊗RM都是n-w-余纯投射的.
证明 设M是n-w-余纯投射R-模,P是有限生成投射R-模,R-模N∈w-ζn.下面考虑以下同构关系
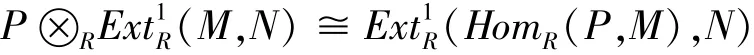
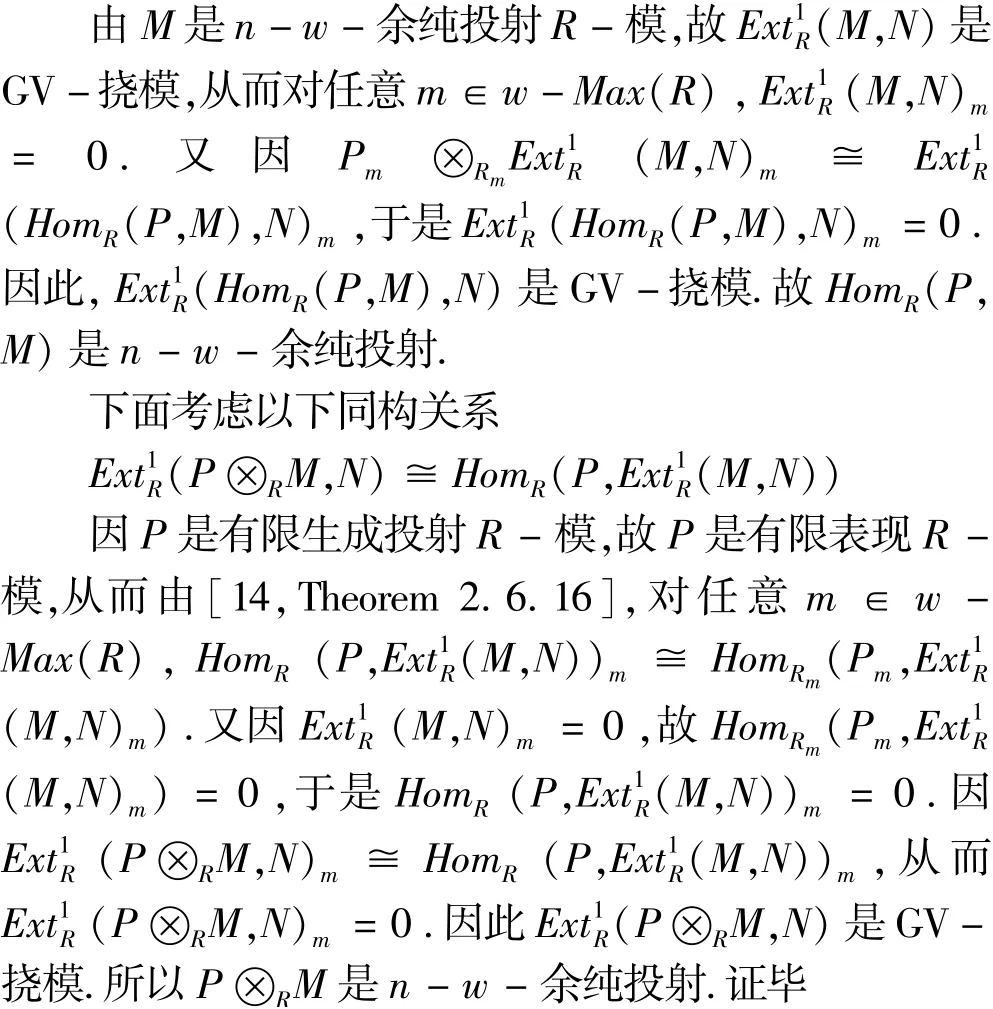
下面我们分别考虑n-w-余纯投射模和强w-余纯投射模在扩张之下的封闭性问题.
定理2.3 设R-模正合列0→A→B→C→0,其中A,C都是n-w-余纯投射模,则B也是n-w-余纯投射模.

定理2.4 设R-模正合列0→A→B→C→0,则
(1)若A,C都是强w-余纯投射模,则B也是强w-余纯投射模.
(2)若B,C都是强w-余纯投射模,则A也是强w-余纯投射模.

命题2.5 设M是w-余纯投射R-模,则M是强w-余纯投射模当且仅当M的第一次合冲(syzygy)是强w-余纯投射模.


定理2.6 设M是R-模,以下各条等价:
(1)M是n-w-余纯投射R模;
(2)对任意R-模正合列0→K→K‘→M→0,其中K‘是n-w-余纯投射R-模,则对任意N∈w-ζn,诱导序列0→HomR(M,N)→HomR(K‘,N)→HomR(K,N)→0是w-正合列;
(3)对任意R-模正合列0→A→B→C→0,其中A∈w-ζn,则诱导序列0→HomR(M,A)→HomR(M,B)→HomRM,C)→0是w-正合列.

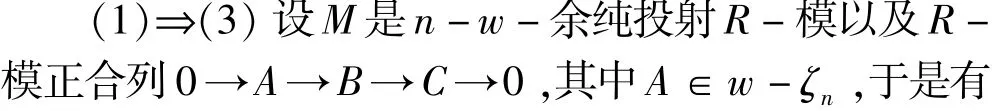

故0→HomR(M,A)→HomR(M,B)→HomRM,C)→0是w-正合列.
(3)⇒(1)设N∈w-ζn,R-模正合列0→N→E(N)→E(N)/N→0,这里E(N)表示R-模N的内射包.于是导出如下正合列

在上述定理中,当n=0时,容易得出如下推论.
推论2.7 设M是R-模,以下各条等价:
(1)M是w-余纯投射R-模;
(2)对任意R-模正合列0→K→K‘→M→0,其中K‘是w-余纯投射R-模,则对任意w-平坦R-模N,诱 导 序 列0→HomR(M,N)→HomR(K‘,N)→HomR(K,N)→0是w-正合列;
(3)对任意R-模正合列0→A→B→C→0,其中A为w-平坦模,则诱导序列0→HomR(M,A)→HomR(M,B)→HomRM,C)→0是w-正合列.

