关于肿瘤增长模型解的适定性研究
樊增欢 蒲志林
(四川师范大学数学科学学院 四川成都 610068)
Cahn-Hilliard 方程最早由Cahn 和Hilliard 于1958年引入[1]用于模拟二元合金相分离的过程。其后,该方程在物理、生物、工程等许多领域的扩散界面模型中得到广泛应用。例如,该方程可以用来描述固体表面上微滴的扩散、生物种群的竞争和排斥、河床迁移过程等[2]。
近年来,扩散界面模型被用于描述肿瘤的生长发展[3-11]。由于肿瘤的生长发展会受到一些生物机制的作用,例如,由营养物质的变化、趋化性以及某些特定的化学物质的作用,从而产生的细胞增殖、凋亡。因此,通常会用反应扩散方程与Cahn-Hilliard 方程耦合形成Cahn-Hilliard 反应扩散界面模型来描述肿瘤发展进程。
文献[12]提出了在考虑趋化性和某些化学物质影响下肿瘤增长的模型方程——Cahn-Hilliard 反应扩散方程:
(1)
该模型对生长核进行了线性稳定性分析,特别是分析了主动输运项的作用。通过数值计算,研究了主动输运项对特定生长情景的影响。
在忽略趋化性和某些化学物质影响下,结合文献[12],本文主要研究如下肿瘤增长模型[13]
φt-Δμ=(Pσ-A)h(φ),(x,t)∈Ω×(0,∞)
(2)
μ=-Δφ+Ψ'(φ),(x,t)∈Ω×(0,∞)
(3)
σt-Δσ=-Cσh(φ)+B(σs-σ),(x,t)∈Ω×(0,∞)
(4)
(5)
φ|t=0=φ0,σ|t=0=σ0,x∈Ω
(6)

与文献[12]相比,本文忽略趋化性和某些化学物质的影响,数学模型变得更加简单;与文献[13]一样,都考虑营养物质浓度对肿瘤相场的影响,但对非线性项Ψ′(s)=f(s)考虑更一般的情况下,研究该偏微分方程系统解存在的唯一性。
1 预备知识和主要结果

令R是带有Neumann边界的Δ算子的弱形式,即令
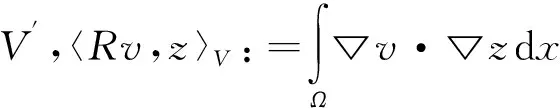
(7)
对于一类定义在Ω的函数(或泛函)v,记v的空间平均值为
(8)
现在,对于任意的ζ∈V′,令
(9)
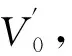
〈Ru,Nζ〉V0=〈RNζ,u〉V=〈ζ,u〉V
(10)
假设1 令系数满足:
P,A,B,C,σs∈(0,1)
(11)
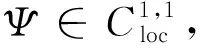
Ψ′(s)=f(s)
(12)

(13)

(14)
f(s)·s≥c1Ψ(s)-c2,Ψ(s)≥-c3,c1,c2,c3≥0
(15)

(16)

最后我们假设初值满足:
σ0∈L∞(Ω),0≤σ0≤1,a.e.x∈Ω
(17)
φ0∈V,Ψ(φ0)∈L1(Ω)
(18)

(a)对于每个T>0,以下正则性质成立:
φ∈H1(0,T;V′)∩C0([0,T];V)∩L2(0,T;H2(Ω))
(19)
f(φ)∈L2(0,T;H)
(20)
μ∈L2(0,T;V)
(21)
σ∈H1(0,T;V′)∩C0([0,T];H)∩L2(0,T;V)∩L∞(0,T;L∞(Ω))
(22)
(b)式(2)-式(6)的解满足以下方程:
φt+Rμ=(Pσ-A)h(φ),x∈V′,a.e.t∈(0,∞)
(23)
μ=Rφ+Ψ′(φ),x∈H,a.e.t∈(0,∞)
(24)
σt+Rσ=-Cσh(φ)+B(σs-σ),x∈V′,a.e.t∈(0,∞)
(25)
(c)以下条件成立:
φ|t=0=φ0,σ|t=0=σ0,a.e.x∈Ω
(26)
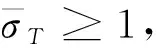
(27)
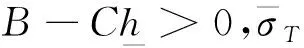
2 定理1的证明
第一步:寻找近似解的先验估计。
首先推理关于营养物质的基本有界性:
第一,对方程(4)用-σ-检验(其中-σ-表示σ的负部),使用h的一致有界性,由于σs>0,且σ≤0可以得到B(σs-σ)是正的。则有:
(28)
然后,由式(17)和Gronwall 引理可知,对每个t>0和x∈Ω,都有σ(t,x)≥0。
(29)
现在分两种情况进行讨论:


(30)
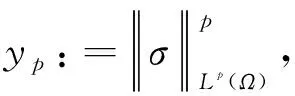
(1+yp)′≤cp(1+yp)
(31)
所以
(32)
因此,开p次方,并且令p→∞,有:
(33)
其中cT表示只与时间T有关的常数。

第二步:推导系统的能量估计。
首先,用μ来检验方程(2),用φt来检验方程(3),加起来有:
(34)
用方程(3)来代替μ,得到:
(35)

(36)
接下来,用σ来检验方程(4),有:
(37)
结合式(35)、式(36)、式(37) 可知:
(38)
用φ来检验方程(2),得到:
(39)
由式(38)、式(39)联立求解,可得:
(40)
因此,由Gronwall 引理,结合不等式(40),可以得到以下先验估计:
(41)
(42)
(43)
(44)

其次,对方程(3)在Ω上积分,得到:
(45)
再结合假设1中的式(16),得到:
(46)
结合式(43),有:
(47)
再结合式(42),可得:
(48)
用f(φ)来检验方程(3),由式(41)和式(47)得到:
(49)
然后,利用椭圆正则性条件等,可以得到:
(50)
第三步:推导关于φ,σ的偏导数的一些估计。
用非零函数v∈V来检验方程(2),得到:
(51)
由式(41),式(48)得:
(52)
用类似的方法检验方程(4),有:
(53)
下面用Faedo-Galerkin 方法[14]证明弱解的存在性及唯一性。
事实上,由式(33),式(41)-式(44),式(47)-式(50),式(52)-式(53) 以及标准的弱紧性理论,可以得到关于n的序列(φn,μn,σn)在Sobolev 空间中弱收敛或者弱*收敛于(φ,μ,σ)。另外,由式(52)、式(53)和Aubin-Lions 引理,可以得到(φn,σn)在Lp空间中强收敛于(φ,σ),因此是逐点收敛的。特别地,结合式(49)和φn是逐点收敛的,并且使用Lebesgue 控制收敛定理,可以得到:f(φn)→f(φ)在L2(0,T;H)中弱收敛,那么根据h和f的连续性可对非线性项取极限,从而得到弱解的存在性。
假设式(2)-式(6) 存在两个解(φ1,μ1,σ1)和(φ2,μ2,σ2),他们相对应的初值分别是(φ1,0,σ1,0)和(φ2,0,σ2,0)。然后令(φ,μ,σ):=(φ1-φ2,μ1-μ2,σ1-σ2)满足以下方程组:
φt+Rμ=Pσh(φ1)+(Pσ2-A)(h(φ1)-h(φ2)),x∈V′,a.e.t∈(0,∞)
(54)
μ=Rφ+Ψ′(φ1)-Ψ′(φ2),x∈H,a.e.t∈(0,∞)
(55)
σt+Rσ=-Cσh(φ1)-Cσ2(h(φ1)-h(φ2))-Bσ,x∈V′,a.e.t∈(0,∞)
(56)
φ|t=0=φ0,σ|t=0=σ0,x∈Ω
(57)
其中令φ0:=φ1,0-φ2,0,σ0:=σ1,0-σ2,0。
特别地,方程(54)在Ω上积分,有:
(58)
用φΩ来检验上面的方程,并利用h和σ2的有界性以及h的Lipschitz 连续条件,可以得到:
(59)
接下来,取式(54)和式(58)的差,并用N(φ-φΩ)来检验,得到:
(60)
用(φ-φΩ)来检验方程(55),得到:
(61)
用σ来检验方程(56),有:
(62)
结合式(59)-式(62),可得:
(63)
由Poincare-Wirtinger 不等式和Ehrling 引理,有:
(64)
对于式(63)项的最后一项
(65)
联立式(63)、式(64)和式(65)得:
(66)
然后,利用式(20),并应用Gronwall 引理
(67)
当(φ0,1,σ0,1)=(φ0,2,σ0,2)得到唯一性。证毕。
3 结论
利用Aubin-Lions 引理、Lebesgue 控制收敛定理、Gronwall 引理以及一些常用的基本不等式,证明了肿瘤增长扩散界面模型在更一般的假设条件下并且忽略趋化性和某些化学物质的影响下,可以得到该耦合方程组初边值问题解的存在唯一性,并且从数学角度解释了浓度σ(t,x)是有界的。

