空腹式拱桥承载力评定及有限元分析

游鹏升 YOU Peng-sheng；潘文超 PAN Wen-chao；袁胜涛 YUAN Sheng-tao；聂良鹏 NIE Liang-peng；许鹏 XU Peng；陈林 CHEN Lin；赵宗惟 ZHAO Zong-wei

（云南通衢工程检测有限公司，昆明650041）

0 引言

拱桥是我国最常用的一种结构承载形式，其样式多，形状美，数量大而成为各种桥型之冠[1]。空腹拱桥的优点是能节省石料，减轻桥的自重，加速洪水的排泄，并能美化桥体的造型[2]-[5]。随着时代的快速发展，我国的公路交通也得到迅猛发展，车辆超载已成为我国十分普遍的现象，桥梁超负荷的运营增加桥梁自身的损伤几率，降低桥梁的安全使用性能[6]。因此，为了明确拱桥的安全运营和承载力真实受力状况[7]。

本文以某座34m 空腹拱桥为依托背景，上承式超高性能混凝土无铰拱桥，主拱拱肋拱轴线为悬链线，计算跨径L=34m，计算失高f=7m，计算失跨比f/L=1/4.86，拱轴系数m=1.543。主拱截面为等截面双箱双室拱肋，每个箱截面高度为1.3m，截面宽度为1.5m。

1 工程概况

该桥位于云南省保山市隆阳区附近，上部结构为单跨空腹式拱桥，跨径为34m，主拱为两个等截面箱型拱肋，每箱截面高度为130cm，截面宽度为150cm；下部结构拱座横桥向长为500cm，纵桥向宽为350cm；桥面横向布置为0.5m（护栏）+7m（车行道）+0.5m（护栏），双向两车道，水泥混凝土路面。桥面铺装由15cm 厚C50 混凝土和无机防水层组成，桥面横坡为2%，设计荷载为公路-II 级。

利用桥梁软件MIDAS/Civil 建立该桥梁格模型并进行分析，通过基本荷载进行试验，在静力荷载下测试上部结构每个截面测点的应力和位移值，比较和分析各截面测点的应力和位移值是否符合设计规范，空腹式拱桥有限元模型如图1 所示，模型共有972 个节点和1090 个单元。

图1 有限元模型

2 桥梁静载试验

2.1 静载试验原则

静载试验主要测试桥梁上部主体结构各控制截面测点的应变、位移、卸载完的残余应变和残余变形[7]，综合评价桥梁主体结构性能。采用载重汽车模拟设计荷载，通过拱肋的影响线并确定加载位置、加载吨位，使其试验荷载效率系数满足规范要求。根据计算分析确定该桥静载试验需载重车的重量，其载重车轴距如图2 所示。

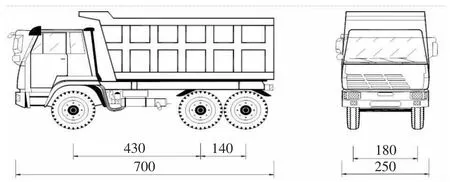
图2 试验车

应变测试：应变片布置于相应测试截面拱肋底部和拱肋顶部，其电阻为120Ω，灵敏度系数为2.08，标距为10cm，并用DH3819 无线静态应变测试仪回收数据。

挠度测试：在各控制截面顶部布设挠度测点，用徕卡全站仪对桥梁挠度进行测量。

2.2 测试截面及测点布置

根据受力最不利的原理，选该桥主拱圈跨作为测试跨，0#拱脚截面J1、L/4 截面J2 和L/2 截面的应力以及变形情况；在每个控制面拱肋顶部及底部布设相应的应变点，沿大里程方向，从左往右，J1、J2 和 J3 断面布设 8 个应变点。

2.3 荷载布置与测试工况

在主拱圈拱肋的J1、J2 和J3 三个截面依次进行加载，每一截面加载车沿横向布置2 辆车，加载方式分为中载和偏载，每一截面加载车沿纵向以相同的方式布置。结构计算按公路-II 级在最不利位置布载，取控制截面最大正弯矩加载截面的控制值，荷载流程详见表1。

表1 荷载试验流程

2.4 静载试验效率

为了满足公路-II 级荷载效应的要求，测试车的数量和轴重是根据控制内力等效原则来选择，使得静载效率ηq介于 0.85~1.05，测试前对加载车进行称重。按式（1）[8]计算：

本次加载以公路-II 级为准，通过布置车位置、加载车辆的重量等调整控制静载效率ηq介于0.85～1.05，该桥静载效率值详见表2。

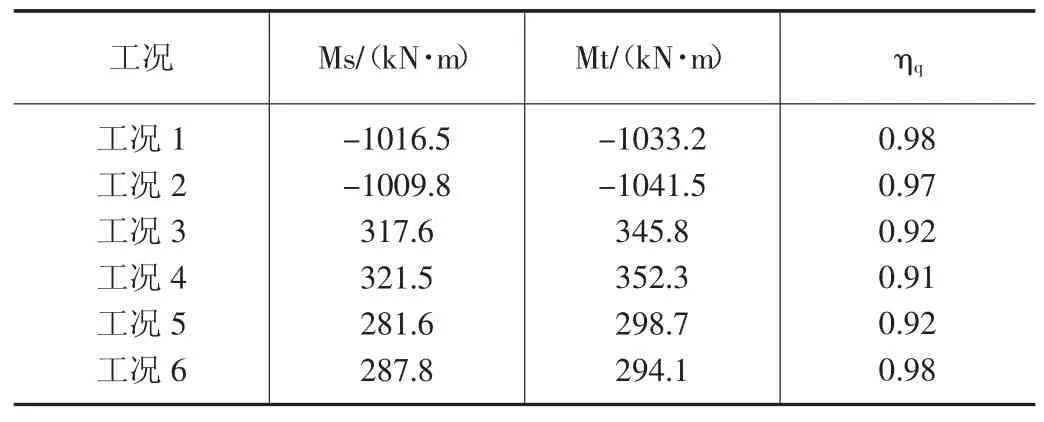
表2 静载荷载效率系数

2.5 试验结果分析

2.5.1 应变测试结果分析

在各工况下，拱肋各测点的应变测试值Se、计算值Ss、残余值 Sp和相对残余值 Sp′如表 3 所示。

从表3 可知，在各工况下，应变校验系数范围为0.36~0.89，说明桥梁结构和材料均符合设计要求，结构整体工作性能良好；相对残余应变值小于14.33%，小于文献[8]规定的允许值20%，说明该桥整体刚度有一定余量，桥梁上部结构处于弹性变形阶段；在受力作用下各测试截面无异常，桥梁整体处于正常受力状况。

表3 实测应变与理论应变的比较

在不同荷载下，各截面的测试应变值沿桥横向变化规律与计算值一致，且测试值均小于理论值，说明该桥横向力传递正常，桥梁整体刚度分布相对均匀。

2.5.2 挠度测试结果分析

在各工况下，拱肋截面测点的挠度实测值fe、理论值fs、残余值 fP和相对残余变形值 fp′如表4 所示。

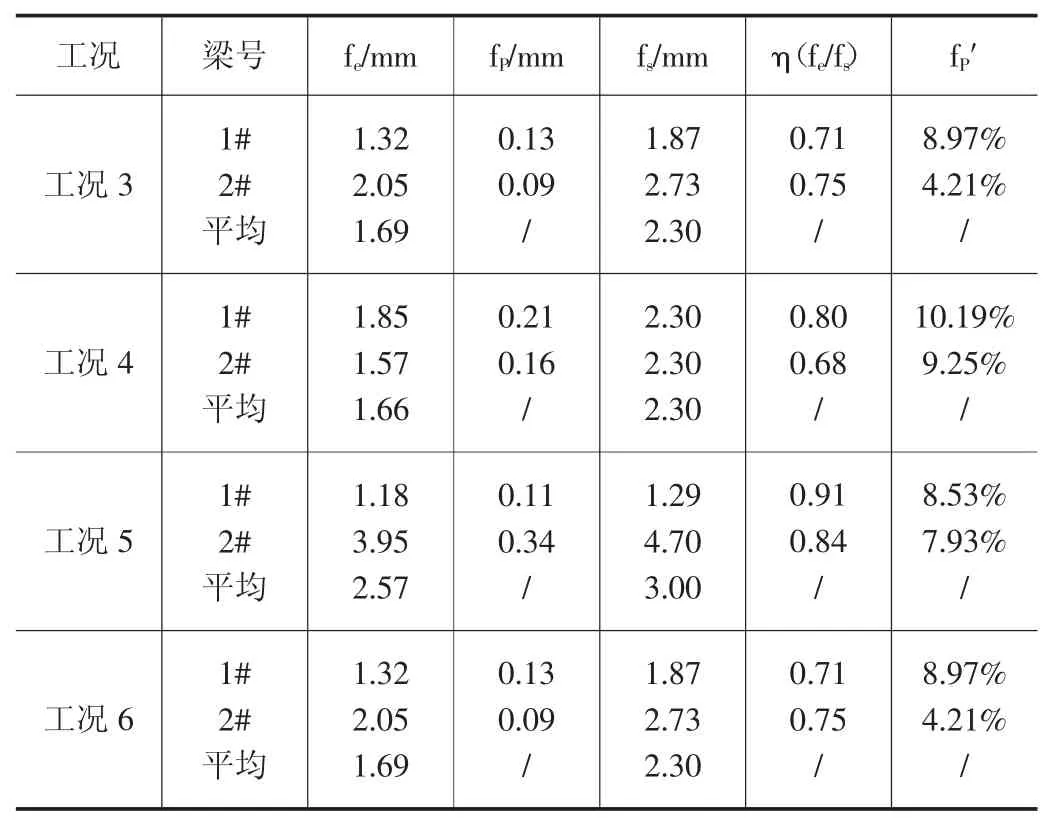
表4 实测挠度与理论挠度的比较

由表4 可见，在每个工况下，挠度校验系数的范围为0.68~0.91，挠度测试值的最大增量为2.57mm 小于规范要求L/600[9]，表明结构的刚度有一定富余度；大部分测量点的残余变形值都为0，表明该桥变形恢复较好，整体结构处于弹性阶段和正常受力状况。

3 桥梁动载试验

3.1 试验内容

本次动力荷载试验主要包括是脉动试验和跑车试验[10]。脉动测试是用DH5907N 无线模态测试仪来测试桥梁自振特性；跑车试验是用DH5908 动态信号测试仪来收集和分析动应变；用1 辆450kN 的特重汽车以10~30km/h速度沿行车道中心线匀速过桥，在移动荷载下测试桥梁上部结构的动应变。

3.2 自振特性结果和分析

根据环境激振下桥梁的动态响应信号和跑车试验的余振信号，可以得出该桥自振特性和阻尼比，其结构自振基本频率测试值与有限元软件计算的理论值见表5。

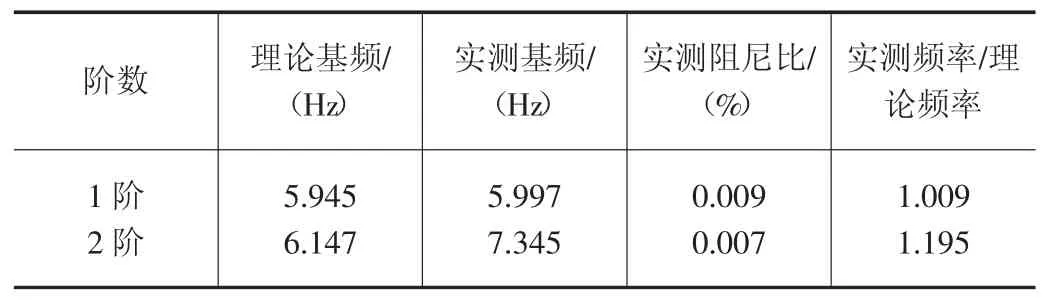
表5 脉动试验结果

实测得到基频高于理论固有基频，表明测得的结构刚度高于理论刚度；一、二阶竖弯实测基频与理论基频比值分别为1.009 和1.195，满足文献[8]≧0.9 要求，表明该桥整体结构刚度较强；一、二阶测试的竖弯振型与理论振型吻合较好，测得前二阶阻尼比分别为0.009%和0.007%，阻尼比很小，表明桥梁整体性能良好，结构具有较强的抗衰减力。

3.3 冲击系数结果和分析

跑车试验选拱肋J1 截面和J2 截面的主拱圈，在行驶车辆荷载作用下测试桥梁上部结构的动态应变。根据跑车试验中动态应变的峰值和谷值来计算应变冲击系数，如表6 所示。根据理论计算基频，试验桥梁理论计算冲击系数μ=0.339。

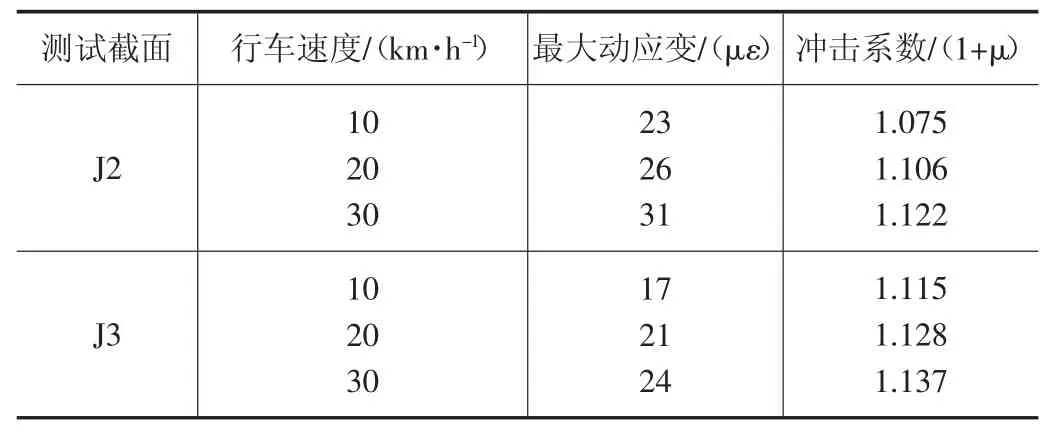
表6 冲击系数测试值

由表6 可知，随着车速的提高，冲击系数呈明显递增的趋势且变化很小，动应变随时间的变化曲线较好，试验测得最大动力系数为1.137，相应的动应变增值为0.137，小于理论计算值0.339，表明桥面行车舒适。

4 结论

①在各工况下，静载效率介于0.91~0.98，在规范允许值0.85~1.05 范围内，说明静载试验成立。②在不同工况下，挠度校验系数介于0.68~0.91，应变校验系数介于0.36~0.89，表明桥梁整体刚度较大且具有一定富余量。③在各工况下，各测点相对残余变形和残余应变值均为0，其中相对残余应变和残余变形最大值分别为14.33%和9.25%，都未超出20%的规范极限值，表明该桥整体处在弹性状况，整体刚度较大。④动力测试结果表明，竖向一阶、二阶振动实测频率与理论频率比值分别为1.009 和1.195，满足规范中≧0.9 的要求；在跑车试验中，动态应变增值为0.137，小于理论计算值0.339，表明桥面行车舒适，桥梁结构满足承载力要求。