基于深度极限学习机的柴油机尾气排放预测
吐尔逊·买买提,赵梦佳,宁成博,孔庆好
(1.新疆农业大学交通与物流工程学院,乌鲁木齐 830052;2.新疆农业科学研究院综合试验场,乌鲁木齐 830012)
近年来,较大的尾气排放总量使得非道路移动源污染物排放问题成为关注的热点。2019年非道路移动源排放NOx、HC、PM等污染物分别达到了493.3×104、43.5×104、24×104t,农业机械等柴油机械排放占非道路移动排放总量的34.3%[1]。可见,农业机械在内的非道路移动源污染气体排放对环境的影响不容忽视。
准确测度排放因子、建立排放清单是大气污染物排放治理以及排放控制的基础。基于各类传感器测量污染物排放因子是常用的方法,但其受到成本、测量精度以及作业状态的限制[2],因此通常采用模型预测方法。目前移动源排放预测方面主要有基于MAP映射、物理模型和数据驱动的污染物排放预测等方法[3]。近年来随着算法框架理论、方法和技术的持续发展,各类预测算法的精度和鲁棒性进一步提高,进而基于数据驱动的预测模型法成为测度污染物排放时间序列的重要途径。Anand等[4]建立反向传播(back propagation,BP)神经网络模型预测柴油机在稳态工况下NOx排放,并验证其模型预测的精度。许金良等[5]基于曲线回归法建立了载重柴油车小半径圆曲线排放量与曲线半径、长度和车辆驶入速度之间的关系模型,并在此基础上建立了累积碳排放模型,并获得了较高的预测精度。
文献[6]基于主成分分析法对数据进行规约,通过网络搜索和遗传算法(genetic algorithm,GA)优化支持向量机(support vector machine,SVM)预测模型参数,并对柴油机不同运行状态NOx排放进行预测,发现和其他方法相比,预测精度较高。左付山等[7]提出了以汽油机排放数据流信息为输入,以汽油机CO、HC和NOx排放水平为输出的BP神经网络的预测。文献[8]提出将最小二乘法和神经网络相结合的预测模型在柴油机NOx排放预测分析方面具有较好的鲁棒性,在较少数据量和非线性拟合方面也有较大优势。分析可知,目前在移动源排放时间序列预测方面,主要针对工程柴油机械排放NOx进行分析,但在农业机械等非道路移动源实际工况排放预测方面的研究尚未见报道。BP神经网络可以作为一种较好的排放预测工具,但BP等神经网络训练速度慢,且容易陷入局部最小化。极限学习机(extreme learning machine,ELM)具有训练时间短、精度高等优点[9],近年来被广泛应用到各个领域[10-12],但目前ELM方法激活函数较单一,模型学习能力较弱,因此需对ELM算法进行优化。
深度极限学习机是一种衍生极限学习机模型,该模型具有训练速度快,泛化能力强等特点。鉴于此,基于实验数据和深度极限学习机(deep extreme learning machine,DELM)方法建立了拖拉机不同运行状态排放预测模型,并于SVM和BP神经网络预测方法进行对比,进而结合实例分析不同模型在排放预测方面的适应性。
1 排放试验及数据预处理
1.1 柴油机排放试验
考虑到新疆拖拉机排放阶段和功率分段等基础数据的可获得性因素,以新疆农机局统计数据和2004年开始实施的农机购置补贴统计数据作为基本依据,结合专家咨询法选取洛阳路通、常州东风、雷沃重工和上海纽荷兰等厂家生产的40~85 kW功率段的5台拖拉机,排放标准均为国Ⅱ,拖拉机具体情况如表1所示。

表1 试验农用拖拉机信息Table 1 Test information of farm tractors
为便于后续分析,选取常州东风拖拉机实地排放数据。田间排放试验研究采用SEMTECH-DS气态污染物分析仪,可以实时采集污染物浓度数据、质量排放量和基于燃油消耗和时间的排放单位,能够应用于车载尾气的测量[13]。通过SEMTECH-DS和GPS模块实时读取GPS移动轨迹、速度、发动机转速、功率、CO、HC、NOx和PM等数据。通过数据接口将数据发送到计算机供后续处理和分析。试验场地选取待犁地的农田,将车载排放测试仪安装到将进行实际作业的拖拉机上。
首先启动测试柴油机进行预热,再安装尾气分析仪,接着校准清零后将其探头放到柴油机的排气管中。尾气分析仪的另一端口可连接到计算机读取数据。将柴油机稳定在怠速状态下运行,被测试的柴油机平稳运行一段时间后,记录此时利用尾气分析仪检测的数据,怠速状态采样时长为600 s。
柴油机在怠速状态下试验结束后,启动设备开关,使柴油机在行走状态下工作一段时间后达到匀速稳定状态,记录尾气分析仪检测到的数据,行走状态采样时长为600 s。
柴油机在行走状态工作结束后,让其于田间边走边旋耕,柴油机处于旋耕状态,记录此时尾气分析仪检测到的数据,行走状态采样时长为1 500 s。
试验前设定采样频率1 s/次,总采样时长为 2 700 s,共采集2 700条排放数据,排放试验周期从拖拉机引擎启动开始到结束为一次。试验测试并记录共有7个参数,分别为转速、油耗流量、燃烧比、CO、HC、NOx和PM。试验获取的部分数据如表2所示。
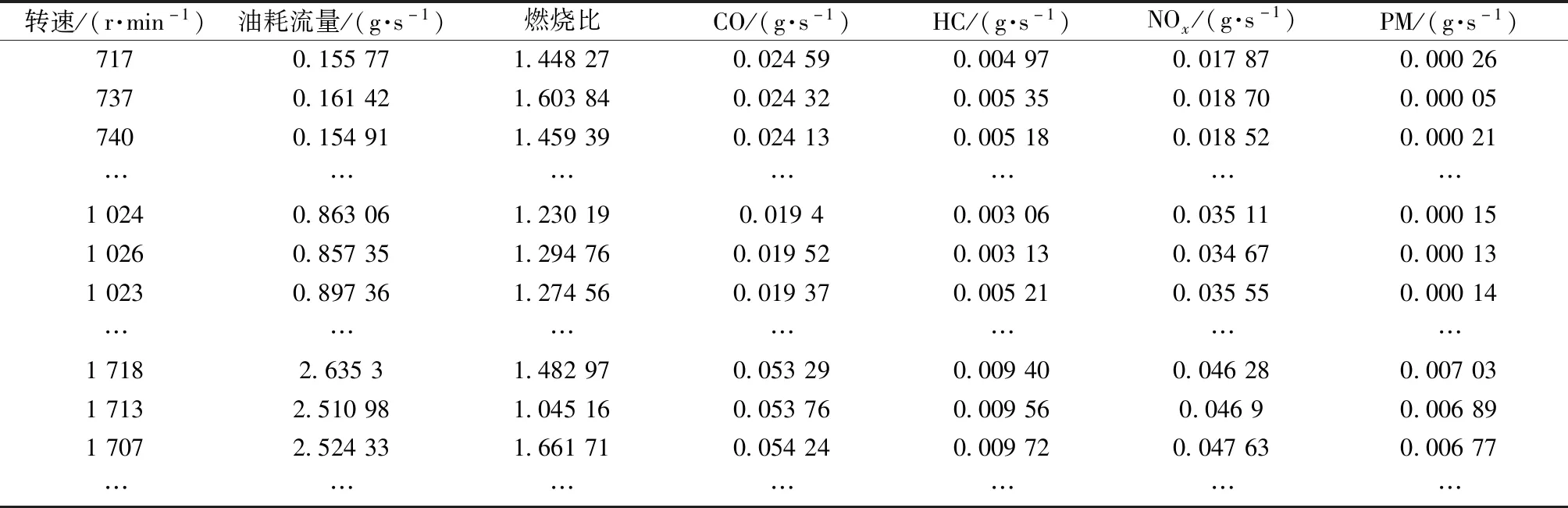
表2 部分试验数据Table 2 Part of the test data
1.2 数据预处理
基于机器学习、神经网络和统计学的预测模型中数据集的属性量纲及值域对模型的预测精度和时间复杂度的影响较大[14]。依据排放试验数据值域分布以及初步建模分析发现,直接进行神经网络训练会降低预测精度,并且增加训练迭代次数。因此在建立排放时间序列深度极限学习机预测模型训练之前对试验数据进行标准化,进而提升模型的预测精度收敛速度。标准化公式为
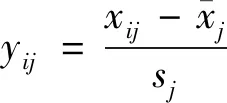
(1)
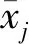
对数据进行标准化后,输出数据每列均值都聚集在0附近,方差为1,可减少神经网络训练的计算量,进而提高模型训练的效率。
2 研究方法
2.1 深度极限学习机方法
ELM是求解单隐含层前馈神经网络的一种算法[15-17],通过随机输入权重和隐含层偏置,计算得到输出层权重[18],从而学习速率快。但因为ELM是单隐含层结构,针对数据较多,数据维度过高等情况,不能捕捉到数据的有效特征,因此更多学者采用ELM的衍生算法DELM。基于此,提出采用深度极限学习机算法对尾气排放量进行预测。
深度极限学习机利用极限学习机与自动编码器相结合[19],形成极限学习机-自动编码器(extreme learning machine-automatic encoder,ELM-AE),再将ELM-AE作为无监督学习的基础单元对输入数据进行训练与学习,并保存ELM-AE由最小二乘法获得的输出权值矩阵用于堆栈深度极限学习机[20-21]。ELM-AE的结构如图1所示。
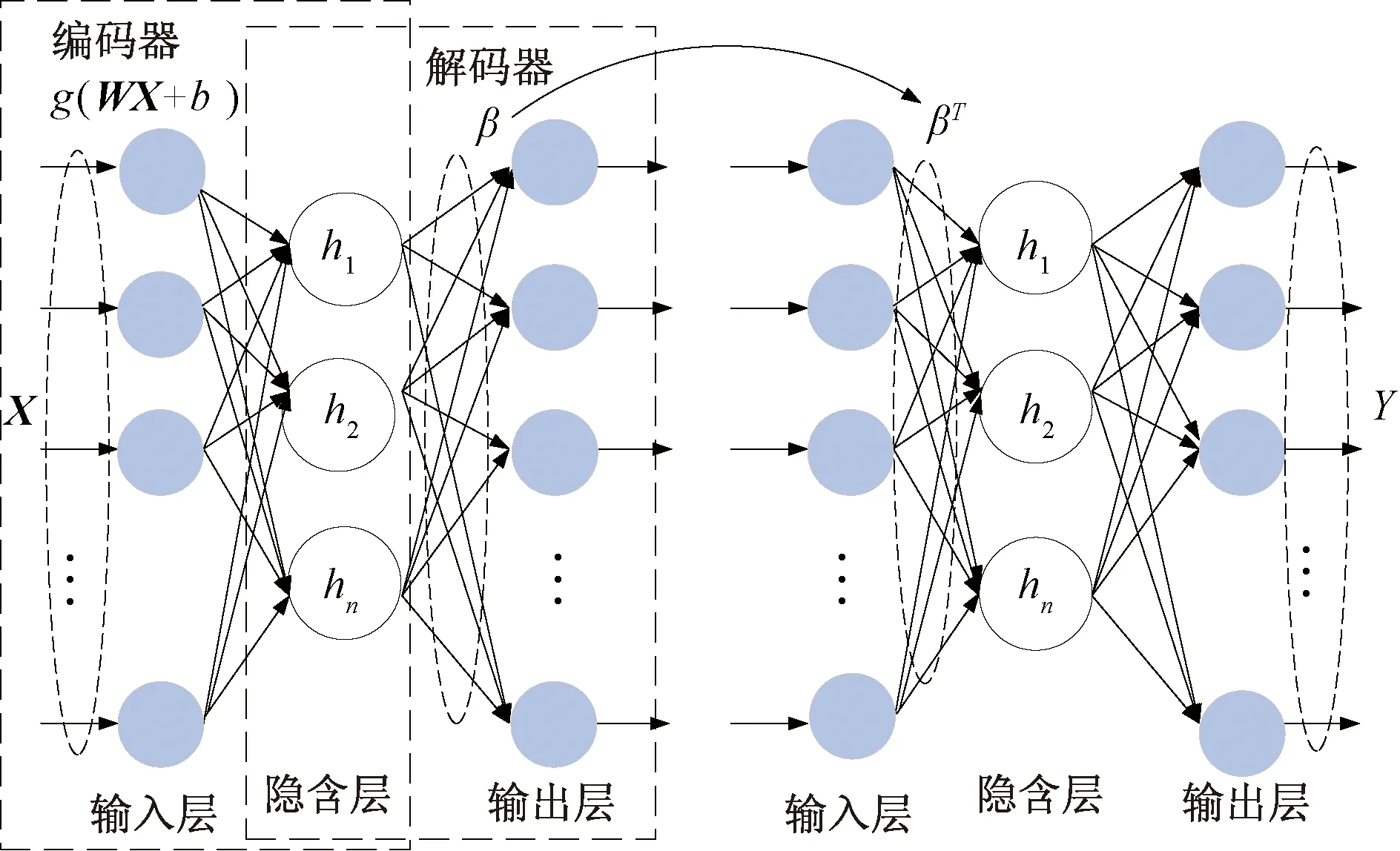
g(WX+b)为隐含层神经元的输出矩阵计算公式;g为激活函数;W为输出层与隐含层之间的权值矩阵;X为输入层矩阵;b为偏移量图1 ELM-AE结构Fig.1 ELM-AE structure
假设给定n个不同的样本集合,xn=[x1,x2,…,xn]T为输入数据;ym=[y1,y2,…,yn]T为输出数据;hx为隐含层的函数;β为连接隐含层和输出层的权重;βT为隐含层和输出层的权重的转置矩阵。
ELM-AE是由输入层、隐含层和输出层构成[22]。输出层权重β可表示为
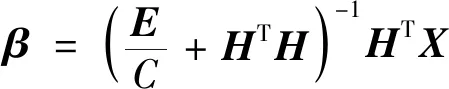
(2)
式(2)中:E为单位矩阵;C为正则化系数;H为隐含层输出矩阵;X为输入和输出。
DELM相当于多个ELM连接在一起,相较于ELM更能全面捕获数据之间的映射关系,从而提高其精确度。且DELM没有反向调优的过程,这样训练网络的时间就会大大减少[23-24],DELM网络结构如图2所示。在训练的过程中,若给定N个样本,输入样本数据为X,DELM模型的隐含层为M,然后依据ELM-AE网络结构得到第一个权重矩阵β1,隐含层特征向量为h1,并作为下一层网络结构的输入。以此类推,最终可得M层输入权重矩阵βM和隐含层特征向量hM,也就完成了深度极限学习机的训练过程。

x为输入数据;β1为连接第一层隐含层和输出层的权重;(β1)T为β1的转置矩阵;hi为隐含层的特征向量;ym=[y1,y2,…,yn]T为输出数据;βi+1为第i+1层隐含层和输出层的权重;(βi+1)T为第i+1层隐含层和输出层的权重的转置矩阵图2 DELM结构Fig.2 DELM structure
2.2 模型数据集划分
数据挖掘中,为提高预测模型的拟合能力和泛化性能,需采用尽可能多的高精度数据对模型进行训练[25]。训练模型时,数据集中训练集和测试集的比例划分对最终的模型精度的影响较大,常用的数据划分方法有留出法、交叉验证法和自助法等。排放试验数据集的划分根据排放时间序列的数据量和值域分布现状应用留出法确定训练集和测试集比例,即取80%的数据作为训练集用于模型的训练,20%作为测试集用于验证预测模型的预测性能。
2.3 模型性能评价指标
所提出的DELM预测模型是使用MATLAB2019a软件编程设计完成。模型性能评价以平均绝对百分误差(mean absolute percent error,MAPE)作为衡量预测模型的精确度的一个重要指标,应用均方根误差(root mean squared error,RMSE)和平均绝对误差(mean absolute error,MAE)指标评价实际输出和预测输出之间的偏差,可较好地评价模型的预测能力。RMSE表示模型的回归精度和学习能力,数值越小,表明该模型的回归能力和学习能力及稳定性越好,MAE和MAPE指标值越小,表明模型预测精确度越高。指标的具体公式为

(3)
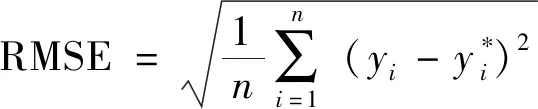
(4)
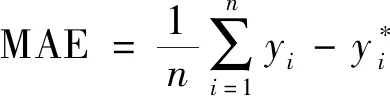
(5)
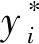
2.4 建模流程
基于DELM的拖拉机排放时间序列预测流程主要包括以下步骤。
步骤1基于SEMTECH-DS平台采集2 700 s获得的发动机转速、油耗流量、燃烧比、CO、HC、NOx和PM等构成原始样本数据集{M1,M2,…,M2 700},其中每个样本包含7个属性,前3个属性为模型输入,后4个为模型输出。
步骤2对原始样本数据集进行标准化处理,得到处理后的样本{D1,D2,…,D2 700}。
步骤3将预处理后的样本数据{D1,D2,…,D2 700}根据拖拉机不同运行状态试验时长分为3个子集{subset1,subset2,subset3},然后将每个子集安1.2.1节中比例划分为训练集和测试集。
步骤4以训练集的发动机转速、油耗流量、燃烧比作为DELM算法输入,CO、HC、NOx和PM作为输出训练拖拉机污染物排放模型。
步骤5基于训练得到的DELM预测模型,将测试集的转速、油耗流量、燃烧比作为输入预测其输出,并通过2.3节模型性能评价指标对其进行分析。
3 结果与分析
基于DELM模型在柴油机3种工况下预测其尾气排放水平。实验过程中,采用气态污染物分析仪实时监测柴油机污染物排放情况,并根据试验数据研究柴油机在怠速、行走及旋耕3种工况下的排放实验结果与预测结果的差异。
3.1 DELM柴油机排放预测
3.1.1 怠速状态排放预测分析
准确预测拖拉机等柴油机械实际工况污染物排放在排放清单建立和区域污染物排放控制方面具有重要意义。首先以怠速状态600个样本为数据源,取其480个样本(即80%)为训练集,并基于深度极限学习机方法和2.4建模流程建立拖拉机怠速状态CO、HC、NOx、PM污染物排放预测模型。然后用训练好的模型和测试集的输入进行预测。最后结合模型性能评价指标分析预测模型。结果如图3所示。
观察图3可知,DELM模型在对拖拉机怠速状态下的CO、HC、NOx、PM预测方面有较好的优势,数据拟合程度较高,为了进一步定量分析其预测精度,应用MAPE、RMSE和MAE 3个评价指标进行分析,结果如表3所示。

图3 怠速状态CO、HC、NOx和PM预测结果Fig.3 CO,HC,NOx and PM prediction result in idling state
由表3结果可以看出,DELM模型在柴油机怠速状态下拟合CO的MAPE为1.547×10-2,RMSE为7.192×10-5,MAE为5.874×10-5,均小于HC、NOx、PM的MAPE、RMSE和MAE值,说明在怠速状态下,CO预测效果较好。PM的MAPE为4.745×10-2,RMSE为2.189×10-4,可以看出,PM的预测误差相较于CO较大,但PM预测值与实际值误差平均值为1.786×10-4,由此可见,预测模型输出结果与实际结果很接近,差值很小,表明DELM模型在柴油机排放预测方面具有较好的拟合学习能力。

表3 怠速状态模型预测误差Table 3 Prediction error of idling state model
3.1.2 行走状态排放预测分析
按照模型数据划分方法确定行走状态600个样本的训练集和测试集。结合建模流程建立拖拉机行走状态CO、HC、NOx、PM污染物排放预测模型。然后用训练好的模型和行走状态测试集的输入进行预测,最后分析其误差,结果如图4所示。
由图4可以发现,行走状态下柴油机排放污染物CO和PM预测值相较于真实值结果偏低,HC和NOx较真实值结果偏高。这可能是因为拖拉机在行走过程中转速不稳定,油耗流量相较于怠速状态下增加,燃烧比增大,进而导致模型训练的数据值有波动,模型预测结果存在偏差;其次在试验过程中,试验采集数据存在干扰异常值,对模型的预测精度有影响。为了进一步分析上述预测偏差的大小,应用MAPE、RMSE和MAE 3个指标对建立的柴油机耕作状态下预测模型的性能进行评估分析,结果如表4所示。
通过表4结果可以看出,虽然在图4中DELM模型预测精度存在一些偏差,但其误差较小。其中,PM预测值的MAPE为1.713×10-2,RMSE为8.031×10-5,MAE为6.496×10-5,均小于CO、HC和NOx的MAPE、RMSE和MAE值,说明在行走状态下,PM预测效果较好。NOx预测值的MAPE为1.806×10-2,RMSE为8.419×10-5,可以看出,NOx的预测误差相较于PM预测误差大,但NOx预测值与实际值误差平均值为6.846×10-5,总体上差值很小,由此可见预测模型输出结果与实际结果很接近,模型具有较高的预测精度,进而表明DELM模型在柴油机行走状态下同样具有较好的预测能力。

表4 行走状态模型预测误差Table 4 Prediction error of walking state model
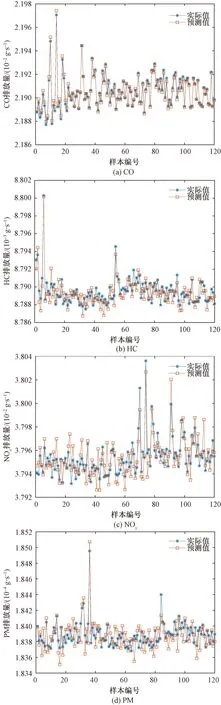
图4 行走状态CO、HC、NOx和PM预测结果Fig.4 CO,HC,NOx and PM prediction result for walking state
3.1.3 旋耕状态排放预测分析
拖拉机结束怠速和行走状态的排放试验后,进入田间进行旋耕作业,此状态具有发动机转速高、燃油消耗和前两种状态相比猛增的特点,同时是排放预测中的重点工况。本阶段首先将取1 500个样本的80%,并训练DELM排放预测模型。然后,基于测试集输入进行预测分析。最后分析其预测性能。为了直观地与其他两个状态下的预测结果进行对比,选取120个预测值制图,如图5所示。
由图5可知,旋耕状态下污染物预测值与真实值趋势大致相同,但存在较大波动,可能是因为拖拉机在旋耕过程中转速上下波动范围相差较大,油耗流量相较于怠速和行走状态过大,柴油燃烧不完全,燃烧比有波动,进而导致数据波动较大,为了进一步解析图中呈现出的趋势,应用MAPE、RMSE和MAE 3个指标对建立的柴油机耕作状态下预测模型的性能进行评估分析,结果如表5所示。

图5 旋耕状态CO、HC、NOx和PM预测结果Fig.5 CO,HC,NOx and PM prediction result for rotary tillage state
旋耕状态下模型的预测结果表明,DELM模型在柴油机旋耕状态预测HC的MAPE为2.320×10-2,RMSE为1.097×10-5,MAE为8.796×10-5。通过表5分析可知,旋耕状态下HC的预测性能均优于CO、NOx和PM,表明旋耕状态下,DELM模型预测HC效果最佳。PM的MAPE为2.847×10-3,RMSE为1.342×10-4,可以看出,PM的预测结果相较于CO预测误差较大,但PM预测值与实际值误差平均值为1.079×10-4,差值较小,且CO、HC、NOx和PM的预测值和实测值的平均绝对百分误差分别为:2.474%、2.32%、2.392%和2.847%,误差值都在5%之内,可以满足较准确地预测拖拉机等柴油机械尾气排放的需要。

表5 旋耕状态模型预测误差Table 5 Prediction error of rotary tillage state model
3.2 不同模型预测性能对比
3.2.1 不同模型预测
为了进一步评估DELM模型的适应性,以CO为例,分别用BP和SVM模型对拖拉机怠速、行走和旋耕工况下CO排放进行预测,并与DELM模型进行对比分析。DELM、BP神经网络和SVM模型不同工况下CO的预测结果如表6所示。
3.2.2 不同模型预测结果对比分析
由表6可以看出,怠速状态下DELM模型预测CO的RMSE、MAPE和MAE均小于BP和SVM模型的预测误差,DELM模型用于柴油机尾气排放预测时,排放预测值与试验实际值之间的平均绝对百分误差仅为1.547×10-2,比BP神经网络和SVM预测模型低98.18%、91.40%,由此可见该DELM模型预测怠速状态下的污染物排放方面和其他2种方法相比优势较明显。
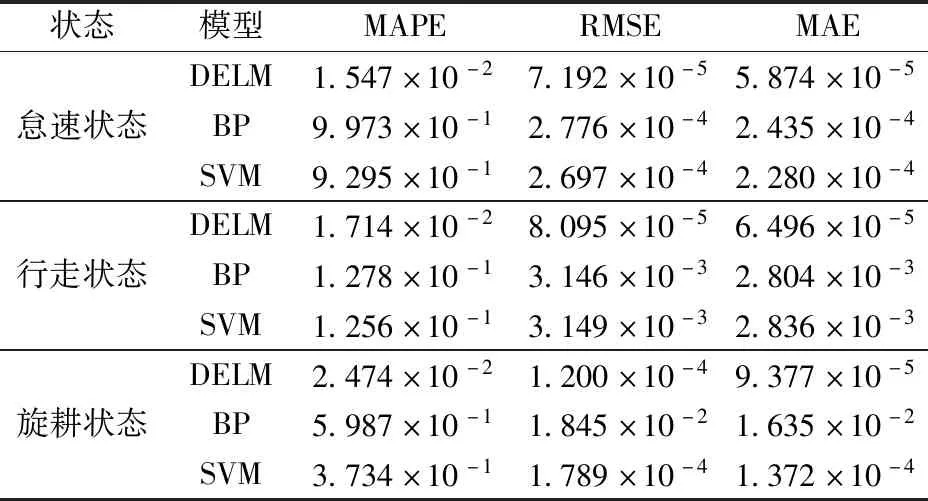
表6 不同状态下不同模型的预测误差对比Table 6 Comparison of prediction errors of different models under different states
不同模型的预测结果对比可知,行走状态下DELM模型在RMSE和MAE误差指标方面比BP神经网络和SVM模型均有所减少,并且DELM模型比BP神经网络和SVM模型的平均绝对百分误差低11.06%、10.85%,表明DELM模型预测精度优于BP神经网络和SVM预测模型。
旋耕状态下DELM模型比BP和SVM模型预测CO的平均绝对百分误差低57.40%、34.87%,对比各项评价指标,DELM模型比其他2种模型的误差值更小,其预测效果也最佳。
综上所述,拖拉机不同工况下DELM模型的预测性能优于BP和SVM模型。SVM预测性能优于BP,这可能是因为BP神经网络容易陷入局部最优而训练失败,从而也导致训练时间较长。然而,DELM模型在训练过程中无需迭代微调,耗时较短,准确率高,在学习速率和泛化能力上具有较强的优势,能快速准确地预测柴油机污染物排放。
4 结论
(1)建立了基于DELM算法的拖拉机尾气排放预测模型,并对怠速、行走和旋耕3种工况下的NOx、HC、CO和PM排放进行预测分析,结果发现,DELM模型预测4种污染物排放均方根误差均值分别为5.269×10-5、5.195×10-5、5.135×10-5和2.795×10-5。表明DELM算法在预测排放时间序列方面具有显著优势。
(2)对比3种模型的CO预测精度发现,DELM预测误差显著低于SVM和BP,表明DELM在预测污染物排放方面较好的泛化能力。
(3)不同运行状态下,DELM模型可为拖拉机等柴油机械的污染物排放时间序列预测提供新途径,进而建立为拖拉机不同工况排放模型提供方法。