面向上甑工艺的机器人作业系统研究
杨 艺,王宏彬,张栗寅,刘 超,,盛鑫军*
(1.上海交通大学机械与动力工程学院,上海 200240;2.海安上海交通大学智能装备研究院,海安 226601)
中国白酒源远流长,在千年的发展过程中,白酒酿造工艺不断开拓创新,形成了包含多种香型的酿酒理论[1-2]。上甑工艺作为酿酒过程核心工艺环节之一,直接决定了出酒率和白酒品质。在上甑过程中,工人师傅将原料分层、均匀、疏松地铺撒在甑锅内,使蒸汽从底部一层一层往上渗透将酒甑中的酒精蒸馏出来,并在铺撒过程中保证不跑汽、不压汽[3]。在现有的绝大部分白酒酒厂中,上甑过程仍需要大量人工完成,通常在上甑过程中,需要两名上甑工人配合通过一个小簸箕将容积接近3 m3的甑锅用甑料填满,其中一个工人负责用铁锨将料堆中的甑料铲入簸箕中,另一个工人将簸箕中的甑料分层均匀地铺洒到甑锅中,在35~40 min的工艺过程中工人们往往要重复成百上千次铲料、铺料的动作,搬运的甑料总质量超过2 t。近年来,随着高精度、高负载工业机器人的发展,工业机器人替代人工完成上甑过程成为了可能。
机器人在酿造行业的应用目前正处于起步阶段,相关研究成果较少,现有的部分酿造上甑机器人往往根据铺满每层甑料设计铺料结构,忽视了人工上甑工艺的传承。例如,文献[4-5]中研发的新型铺料机构以及专利[6]中的上甑机器人,上甑动作按照预定的轨迹执行,二者均能完成基本上甑功能,然而同人工上甑工艺区别较大,在部分区域由于姿态限制难以完成漏汽补料任务。
基于此,在上甑工艺环节,从传承人工工艺手法出发,通过对人工上甑过程进行动作数据采集,提出一种基于样条曲线-高斯概率模型的泛化方法,得到人工上甑工艺的标准轨迹。通过对轨迹和实际人工上甑过程的分析,规划更加贴近人工上甑过程的上甑轨迹,设计并制作甑料流速可控的末端料斗机构,选用埃夫特ER-210D六轴工业机器人作为执行器,实现仿人上甑轨迹的机器人自动上甑过程。在上甑过程中,利用工业机器人的动力学特性得到轨迹最大速度,配合末端料斗机构的甑料流速控制实现每层的给定厚度铺洒,在保证“轻撒匀铺”工艺要求的同时,尽可能提高上甑效率。
1 人工上甑工艺泛化与提取
1.1 基于动态时间规整算法的时间对齐
在人工上甑的过程中(图1),将三颗红外反射小球固定在簸箕边缘上,利用如图2所示的Nokov红外动作捕捉系统采集上甑过程中簸箕的空间运动轨迹。

图1 上甑动作数据采集Fig.1 Motion data acquisition of the caldron

图2 Nokov红外动作捕捉系统Fig.2 The Nokov infrared motion capture system
对于人工来说,同一上甑手法的铺洒动作无法做到每次的轨迹和速度一致,在同样采样频率下采集得到的簸箕数据往往存在一定的随机性和变形。对于空间上的变形,定义为在空间约束下允许的变形满足某种概率分布,因此属于示教学习系统模型需要泛化的一部分。对于时间上的变形,其会导致各次示教数据的时间序列非完全同步,若不经预处理,直接将时间显性作为训练数据进行模型提取,会严重影响模型的精确性。故而,在进行空间上的轨迹泛化前,需要对同一手法的多次簸箕轨迹进行时序规整,其本质是寻找若干组时序映射使多次示教数据中的点对建立对应关系。
令Q={q1,q2,…,qn}为长度为n的参考数据,其中qi对应参考轨迹某时刻的采样数据,总时长为TQ;令P={p1,p2,…,pm}为长度为m的待规整数据,其中pi对应待规整轨迹某时刻的采样数据,总时长为TP。qi与pj的维数应保持一致,两者在采样过程中保持采样频率恒定。时序统一规整方法即是寻找限制下的某时序映射关系:
TP=f(TQ)
(1)
使待规整轨迹映射后,所有对应点的数据差在某度量下最小:
(2)
对于三维空间的位置点,采用位置误差作为度量标准,则函数g(x,y)的表达为
(3)
动态事件规整算法(dynamic time warping,DTW)[7]是一种建立时序映射关系的算法,其算法原理如图3所示。

图3 DTW算法原理示意图Fig.3 The schematic diagram of DTW algorithm
对于两条长度分别为m和n的轨迹数据q1和q2,可构建m×n阶矩阵M,矩阵中各元素含义为
M(i,j)=g[q1(i),q2(j)]
(4)
即M(i,j)表示q1中第i个数据与q2中第j个数据在三维空间中距离,而时序规整的目的是从M(1,1)起,找出一条最短的连续路径s。
s=[M(i1,j1),M(i2,j2),…,M(ik,jk)]
(5)
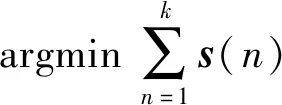
(6)
对于路径中的任一点M(i,j),为防止数据丢失即保证路径连续且方向递增,则下一组对应点有三种可能:M(i+1,j)、M(i,j+1)和M(i+1,j+1),从i=j=1开始,每次选择移动到路径增长量最小的下一个点,一直到i=j=max(m,n)。图中经过的点对代表最后得到的新的配对序列s(k)。动态时间规整的物理意义是对于两条路径上的点,从第一个点依次开始找出三维空间上距离最短的下一组相邻点作为新的序列在该时刻的对齐点,其依据是对于同一种上甑手法的多次动作数据,在消除工人上甑速度不一致导致的时序变形后,新的对齐序列在空间上的变形应尽量小。
DTW使用的简单度量函数g仅假设距离较近的点有配对关系,忽视了速度、加速度等信息,在应用于振荡严重的动作数据时,容易产生点对错误匹配导致奇点问题[8],还会造成连续性问题。如图4所示,A曲线为原始示教轨迹对,B为基于动态时间归整算法的轨迹匹配结果。图中可知,简单度量函数g在振荡严重的轨迹上引起点对错误匹配,而错误匹配又引起某轨迹单点对应其他轨迹多点,带来不连续性问题影响后续模型提取过程。
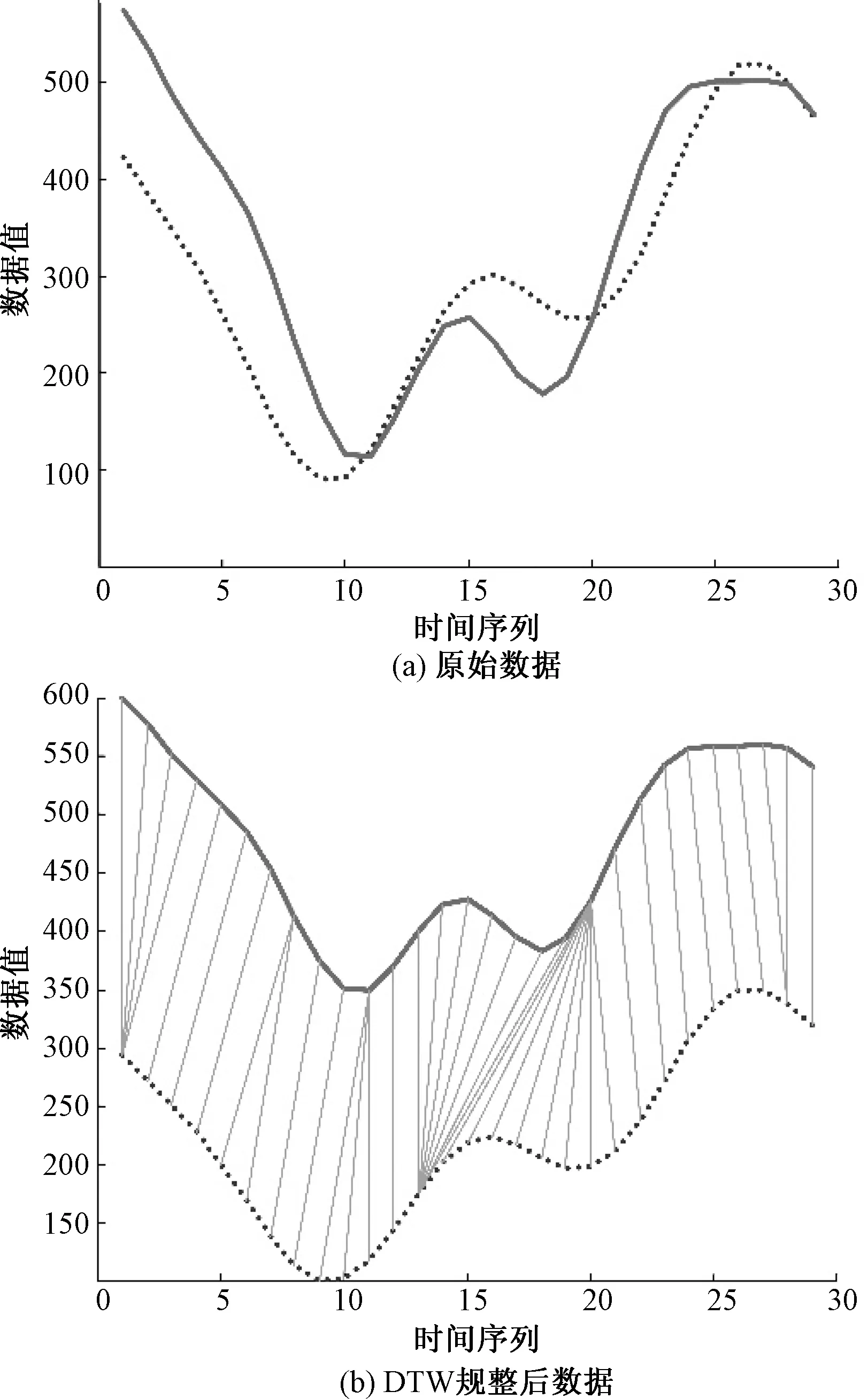
图4 DTW算法缺陷Fig.4 The defects of DTW algorithm
为增加规整算法对形状的感知,采用一阶导数替代簸箕轨迹的空间位置数据,利用形状上特征与特征的对应来寻找时间规整轨迹(derivative dynamic time warping,DDTW)[9]。对于长度为nq的动作数据序列q,其导数序列Cq为

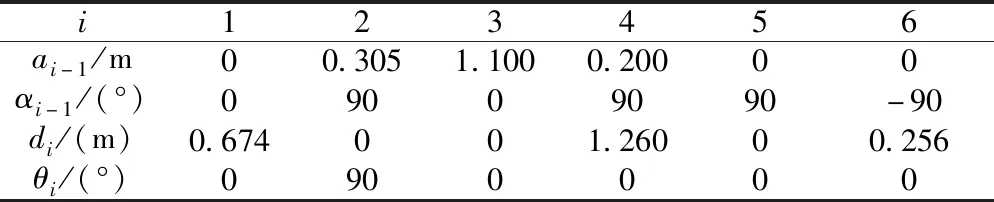
2 (7) Cq(0)=Cq(1),Cq(m)=Cq(m-1) (8) 为测试算法性能,使用式(9)生成仿真数据: (9) 图5 第三维噪声下时序规整效果Fig.5 The result of time warping under the influence of noise in the 3rd dimension 对于时序规整后的簸箕轨迹数据,假设每个时序对应的数据组在空间中符合高斯概率模型,多维高斯概率模型表达式为 (10) 式(10)中:d为变量维度;μ为n维向量,代表各维变量的均值;Σ为协方差矩阵,描述各维变量之间的相关度。假设泛化提取后的簸箕轨迹为X=F(t),其中X为6维向量,前三维为每时刻高斯概率模型的均值,其物理意义为泛化后轨迹曲线的空间坐标,后三维表示每时刻高斯概率模型的方差,对于k组对齐后的动作数据,同一时刻的数据组yt为同一高斯概率模型,高斯概率模型的似然概率为 g{yt|u[X1∶3(t)],σ[X4∶9(t)]}= (11) 假设对齐后的数据序列长度为N,若存在轨迹X使得各时刻高斯概率模型的似然概率和达到最大,则定义该轨迹为上甑工艺的标准轨迹,泛化的最优化问题可表述为 (12) 为使拟合的泛化轨迹光滑柔顺,以三次B样条曲线替代轨迹X进行优化。B样条曲线的表达式为 (13) 式(13)中:Ni,k(u)为基函数;Pi为第i个控制点。Ni,k(u)利用递推公式定义为 (14) (15) 式(15)中:ti为节点值;T=[t0,ti,…,tL+2k+1]为节点矢量;L=n-k且节点是非减数列。均匀B样条曲线指节点沿参数轴均匀分布,即 用权重矩阵和控制点矩阵简化B样条模型可得 本文提出的脆弱性评估的思想和方法,有一定的创新意义,但在实际操作中还有很多需要改进和完善的地方,更重要的是,它还需要与其它方法结合使用,进一步的扩展到整个国家受气候变化影响的脆弱性评估中。由于干预原因具有不确定性,我们采取的模型单一,可能对结果造成误差。 x(t)=A(t)·θ (16) 式(16)中:x∈RN×d,N表示示教轨迹的点数,d表示B样条曲线维度,x表示任意时刻高斯模型参数的拟合值;A∈RN×p,p表示控制点数量,A(i,j)表示控制点j在i时刻的权重,即 A(i,j)=Nj,3(i) (17) 优化问题转化为 (18) 函数σ(x)将向量转为对称矩阵,定义为 (19) 优化函数代入式(11)取自然对数后可等效为 (20) 求偏导: σT[A(t)·θ4∶9] (21) (22) 式(22)中:σ*[A(t)·θ4∶9]表示矩阵σ[A(t)·θ4∶9]的伴随矩阵,根据偏导数求出下降方向,利用最速下降法求解loss函数最小值,即原优化函数最大值,最终得到泛化轨迹如图6所示。 图6 人工上甑轨迹泛化结果Fig.6 The generalization results of the artificial caldron-feeding trajectories 从图6可知,人工上甑时由于工人臂展限制,在进行远端铺料时,工人往往通过抛洒的方式以离心力将甑料洒到远端。各条上甑轨迹泛化结果在形状上相似,均为以工人站立点为圆心的类圆弧型轨迹,各条轨迹距离人工站立点的距离不同,距离越远代表铺洒距离越远。 采用机器人上甑时,末端料斗机构容积、质量与人工上甑时使用的簸箕差距大,机器人的抛洒的结果与人工相差很大,故本文采用垂直铺洒的方式实现机器人上甑,甑料从机器人末端料斗机构垂直下落铺洒,并带动末端料斗机构覆盖整个上甑平面。从图7中近端轨迹特征结合工人实际上甑流程可以看出,外层溜边铺洒为以甑锅中心为圆心的圆弧形轨迹铺洒,内层按距工人的远近分为近、中、远三层,每次铺洒的甑料都是以工人站立点为圆心的圆环区域,由此,本文将甑锅内任意上甑平面分为如图7所示8个区域。机器人末端料斗机构如图8所示。 区域①和⑤为甑锅外侧铺洒,区域②~④和区域⑥~⑧为内层铺洒。区域②~④和⑥~⑧的铺洒方向不同,②~④为逆时针铺洒,⑥~⑧为顺时针铺洒图7 甑锅内上甑平面分割Fig.7 The area separation result of the working plane in caldron 图8 末端料斗机构Fig.8 The hopper mechanism 装置外侧框架有方形管焊接组成,内侧由不锈钢板包围形成包围盒容纳甑料,底部为电机控制的主动传送带,料仓内安装电动滚筒焊接形成的钉耙滚筒。甑料密度约为1 000 kg/m3,整体物理性状为粘稠泥沙状物料,料斗机构底部与水平方向呈30°,此时甑料与传送带间的黏性摩擦力与重力接近抵消,整个机构通过底部主动传送带控制甑料的下料速度,滚筒钉耙的作用是打散被压实的甑料,保证下料顺畅、均匀、松散。末端料斗机构总质量76 kg,满载能容纳甑料质量为35 kg,上甑系统采用埃夫特ER-210D机器人(最大负载为210 kg),末端总质量符合机器人负载要求。 末端料斗机构的下料情况由传送带转速ω1和滚筒钉耙转速ω2控制。根据料斗机构的工作原理,末端料斗机构流出的甑料完全由底部传送带从料仓中送出,因此单位时间内下料总量由ω1控制。甑料从出料口流出时,甑料脱离传送带后在重力作用下在近端坠落。滚筒钉耙的主要作用是将压实的甑料打散。设料斗机构的下料速度控制函数为f(ω1),并通过实验测定。 进行实验时,控制机器人将末端装置以上甑姿态移动到称重传感器和亚克力板组成的测量平台上方,改变传送带电机转速ω1,记录不同转速下装置单位时间内下料质量如图9所示。 图9 下料质量流速与传送带电机转速关系Fig.9 The relationship between the mass flow rate of the hopper mechanism and the speed of the conveyor motor 由实验结果可知,料斗机构的下料质量流速与传送带电机转速的关系可拟合为一条直线,直线表达式为 vm=f(ω1)=1.19ω1+0.29 (23) 为得到每条铺洒路径的笛卡尔姿态轨迹,以区域①的铺洒为例,工作空间的俯视图及各坐标系位置关系如图10所示。 图10 工作空间各坐标系相对关系示意图Fig.10 Schematic diagram of the relative relationship of each coordinate system in the workspace 坐标系{xOy}、{x1O1y1}、{x2O2y2}、{x3O3y3}分别为机器人基座坐标系、机器人末端法兰坐标系、固结于末端料斗机构出料口中点的物体坐标系和固结于甑锅底面圆心的物体坐标系。末端料斗机构通过螺钉固定于机器人末端法兰盘,坐标系{x1O1y1}、{x2O2y2}的相对位姿始终保持不变,三个坐标系间的转换关系为 (24) (25) 在上甑工作时,末端料斗机构在竖直方向投影为图10中左图所示长h宽d的矩形,在进行区域①铺洒时,末端料斗机构出料口中点O2的运行轨迹为与甑锅同圆心半径为r的左半圆。为防止碰撞,以末端料斗机构长度h为弦长的圆弧半径R应略小于当前甑料面半径。甑锅形状为上直径2 m、下直径1.8 m、高度1.2 m的圆锥台,设当前铺料面在甑锅内高度为H,甑锅底面圆心O3在机器人基座标系{xOy}下位置为[XYZ]。从坐标系{xOy}到坐标系{x2O2y2}的坐标变换分为三步,第一步将坐标系{xOy}平移到运动路径的圆弧r上,第二步坐标系{xOy}绕x轴旋转180°使z轴向下,第三步坐标系{xOy}绕z轴旋转α使料斗不与甑锅碰撞,则坐标转换矩阵可表示为 θ∈[0,π] (26) (27) (28) (29) 上甑机器人末端料斗机构由滚筒和底部传送带配合送料,铺料的定厚控制有两种策略,第一种是在铺料过程中充分发挥机器人性能,使机器人在铺料轨迹中达到时间最优,通过不断调节末端料斗机构下料速度配合机器人实现定厚铺洒。第二种是机器人在执行各条铺料轨迹时采用固定的笛卡尔速度匀速铺洒,对该过程进行动力学分析,在满足机器人载荷的条件下找出最大的笛卡尔速度,然后依据该笛卡尔速度结合末端料斗机构的出料控制函数找到合适的出料速度,在不需要频繁改变末端机构的电机转速也可在较短时间内实现给定轨迹给定厚度的甑料铺洒。在实际上甑使用中,第一种策略中,虽然传送带和滚筒速度可调,但由于加减速过程的存在无法做到及时矫正下料速度,难以配合机器人不断变化的笛卡尔速度实现给定厚度的铺洒,因此本文采用第二种策略进行作业研究。 基于2.3节计算的机器人笛卡尔铺洒轨迹,现首先建立机器人的运动学模型,通过机器人逆运动学将笛卡尔轨迹转化为关节空间轨迹,然后参照机器人物理参数建立机器人的动力学模型,从各关节的轨迹导出各关节的力矩曲线,通过与各关节最大力矩限制对比,计算出符合各关节力矩限制条件的最大笛卡尔速度。 机器人上甑系统采用埃夫特ER-210D机器人作业,其尺寸参数如图11所示。 图11 埃夫特ER-210D机器人尺寸参数Fig.11 The parameters of EFORT ER-210D robot 该机器人为六轴工业机器人,末端三传动轴轴线相交形成球腕。采用改进的D-H参数法[10]建立机器人各连杆坐标系,完成机器人的运动学建模。坐标系建立方法如图12所示,在此参数法中使用扭转角αi-1描述关节i-1的轴线zi-1到关节i的轴线zi绕坐标轴xi-1的转角;连杆长度αi-1描述沿着坐标轴xi-1将zi-1移动到zi的距离;关节偏距di表示沿着轴线zi-1使得xi-1与xi重合的移动距离;关节转角θi表示关节i绕着zi轴将xi-1旋转到xi的转角。 图12 改进的D-H参数法Fig.12 The improved D-H parameter method 相邻连杆坐标的齐次转换矩阵可表示为 (30) (31) 图13 埃夫特ER-210D机器人D-H坐标模型Fig.13 The D-H coordinate model of EFORT ER-210D robot 表1 埃夫特ER-210D机器人D-H参数Table 1 The D-H parameters of ER-210D robot 埃夫特ER-210D机器人后三轴为轴线相交的球腕模型,图13中点P4-6为轴线交点,其在空间中的位置完全由机器人前三轴角度确定。若某时刻机器人末端在空间中的位置为[xt,yt,zt],机械臂末端坐标系相对于基座坐标系的旋转矩阵为Rt,则后三轴轴线通过的同一点P4-6的位置,可知: (32) (33) (34) 式中:si=sinθ1,ci=cosθ1,sij=sin(θ1+θ1),cij=cos(θ1+θ1)。由式(32)和式(34)前两项可求出: (35) 若sinθ1非0,将θ1代入至y4-6方程两边同除sinθ1,若sinθ1为0,则将θ1代入至x4-6方程两边同除cosθ1,与z4-6方程组成方程组后可化简为 Asinθ2+Bcosθ2=C (36) (37) B=2.2z4-7-1.482 8 (38) 0.417 6 (39) 式中: 由辅助角公式可得 (40) 式(40)中:θ2∈[-80°,60°]。将θ2代入式(32)和式(34)中z4-6方程,同理,由辅助角公式可得 (41) 式(41)中:θ3∈[-83°,90°]。该机器人后三轴旋转矩阵为 (42) 对应项连立为9个方程组,参考文献[11-12]的求解方法,其解为 θ4=atan2[R4-6(1,3),-R4-6(2,3)] (43) (44) θ6=atan2[R4-6(3,1),-R4-6(3,2)] (45) 式中:R4-6(i,j)表示取R4-6矩阵的i行j列。函数atan2的定义如下: (46) 由式(35)~式(46)可知,当机器人末端位姿可知时,可反解出机器人各关节角度,实现机器人运动学逆解。 机器人牛顿-欧拉动力学状态方程[13]为 (47) 在SolidWorks中,通过对机器人三维模型的质量仿真,得到机器人的各连杆参数如表2所示。 表2中,mi为连杆i的质量其中连杆6为末端法兰盘和满载的料斗机构固定形成的等效连杆,[rx,i,ry,i,rz,i]表示连杆i的质心在连杆坐标系{i}中的向量,[Ix,I,Iy,I,Iz,i]表示连杆i在质心坐标系中的惯性矩。牛顿-欧拉动力学逆解的过程[14]为先从基座到末端工具坐标系推导各连杆质心的角速度/角加速度、速度/线加速度,根据牛顿第二定律建立各连杆的受力方程,然后从末端工具坐标系向基座逆推,依次求解各关节向下一连杆所需提供的力矩。借助MATLAB中的Robotics Toolbox工具箱[15]完成机器人的动力学逆解问题。 表2 埃夫特ER-210D工业机器人连杆物理参数Table 2 The physical parameters of each link in ER-210D robot 基于2.3节中求出的上甑机器人在不同区域铺洒作业时机器人末端工具坐标系的笛卡尔位姿轨迹,根据位姿轨迹和机器人的运动学逆解模型求解出各轨迹对应的关节空间轨迹。以铺洒区域①为例,机器人的末端的位姿轨迹方程可由式(24)~式(29)表述,对该轨迹中的各位姿进行反解,各关节的角度变化曲线如图14(d)所示。设定末端料斗机构铺洒时的速度恒定为0.14 m/s,通过动力学反解模型解出该轨迹上甑过程中各关节的力矩曲线如图14(b)和图14(c)所示。 图14 速度0.14 m/s动力学逆解结果Fig.14 The inverse solution of robot dynamics at the speed of 0.14 m/s 机器人各关节轴线,即各连杆坐标系的z轴,从图13的D-H模型中可以看出,机器人1轴轴线为竖直方向,主要承受后续结构的重力弯矩,在上甑工作时其力矩在前三轴中属于较低水平。机器人的2轴提供机器人在竖直平面内运动的大部分扭矩,通常在前三轴中为最大。而3轴提供了后续结构在竖直平面的部分扭矩,其扭矩位于二者之间。机器人4~6轴的主要作用是调节末端姿态,力臂较小,因此在姿态变化并不剧烈的作业中所提供的扭矩往往远小于前3轴。图14中曲线与实际情况相符,说明了机器人动力学反解模型的合理性。 从埃夫特ER-210D机器人手册可知,各轴的最大可提供力矩(N·m)为 (48) 针对不同的末端铺料速度,计算出每个轴的最大负载比,即过程中所需最大力矩与最大可提供力矩的比值,各轴的最大负载比与末端速度的关系如图15所示。 图15 区域1铺洒速度与各轴最大负载比关系图Fig.15 The relationship between the maximum load ratio of each axis and spreading speed in area 1 以最大负载比不超过80%为安全限制条件,可以得到区域一上甑轨迹的最大速度为0.4 m/s。按照上述过程对其余7个区域的上甑轨迹进行计算,得到所有轨迹末端料斗机构的最大速度(m/s)为 (49) 对于轨迹i,设末端料斗机构的速度为v,末端出料口宽度为l=0.4 m,甑料密度ρ≈1 000 kg/m3,则在时间dt内,由出料平衡可得 vdtlhρ=f(ω1)dt (50) (51) 铺料厚度h的控制函数如式(23)所示,每条铺料轨迹的最大末端料斗机构速度v由式(49)可知。两式联立,即可解出每个区域实现任意铺料厚度所需的末端料斗机构传送带电机转速。 以所需厚度25 mm为例,计算各轨迹所需传送带电机转速(rad/s)分别为 (52) 机器人按照给定轨迹和速度,末端料斗机构按照给定转速进行铺洒,完成完整一层甑料铺洒之后,通过固定在末端料斗机构上的红外测距传感器测量该层甑料的铺洒厚度,结果如图16所示。 图16 定厚25 mm实际铺洒效果Fig.16 The actual paving effects with a fixed thickness of 25 mm 由于末端料斗的流速控制关系为拟合函数、料斗的泥沙状物理特性影响,从图中可以看出铺洒出的甑料厚度波动较大,但从整体来看,波动范围未超过5 mm,厚度平均值为24 mm,厚度控制策略效果显著。 经过15次机器人单机上甑实验,每次上甑时间分布如图17所示。 图17 上甑实验时间数据记录图Fig.17 The record chart of time cost in all caldron feeding experiments 从实验数据可以看出,机器人单机完整上甑时间(min)分布在[26.2,31.7]区间内,平均上甑时间为29.04 min,相比与人工上甑时间35 min缩短了18%,证明了机器人自动上甑效率相对人工上甑效率更高。 以下层甑料铺洒前锅内甑料高度测量值减去上层甑料铺洒前锅内甑料高度,可测量每层甑料厚度,取当次上甑过程中每层厚度的平均值作为当次实验每层甑料厚度,15次实验内每层甑料厚度变化如图18所示。 图18 上甑实验每层厚度记录图Fig.18 The record chart of the thickness of each layer in all caldron feeding experiments 从实验数据可以看出,在15次上甑实验中平均每层上甑厚度为23.94 mm,与期望厚度25 mm误差很小。同时,每次实验的每层甑料厚度也均在人工上甑工艺所要求的20~30 mm范围内。综上所述,15次上甑实验证明了该机器人上甑系统不仅在符合人工上甑工艺要求的条件下提高了上甑效率,而且每层上甑厚度也具有良好的稳定性。 面向白酒酿造过程中的上甑环节,通过分析上甑师傅典型作业手法,设计开发了一套面向上甑工艺的机器人作业系统,并对其关键技术进行了重点研究分析。首先,提出了一种基于样条曲线-高斯模型的上甑轨迹泛化编码算法,该算法假设上甑过程中的重复动作在任意时刻的数据点符合高斯分布,利用三次均匀B样条曲线表征所有时刻的高斯分布参数,使用最大似然估计构造优化得到最终的样条曲线参数.并通过采集人工上甑的动作数据,结合泛化模型得到人工上甑工艺在空间中的轨迹信息。其次,重点分析人工上甑的工艺特性,不仅对机器人上甑区域进行了分割,而且设计了甑料流速可控的末端料斗机构,结合现场布局对每个区域的铺洒轨迹进行计算。之后,通过建立机器人动力学逆解模型,根据机器人各关节负载限制得到每个区域的最大速度,结合末端料斗机构的伺服控制制定上甑作业时铺洒厚度的控制策略。最后,通过15次上甑实验数据验证了本文所设计的机器人上甑作业系统的有效性,在保证每层上甑厚度符合工艺的前提下,将每次的上甑时间相比人工缩短了18%。
1.2 基于高斯概率模型的轨迹泛化方法
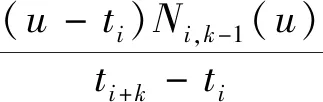

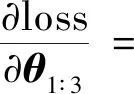

2 末端料斗机构与上甑轨迹规划
2.1 末端料斗机构设计

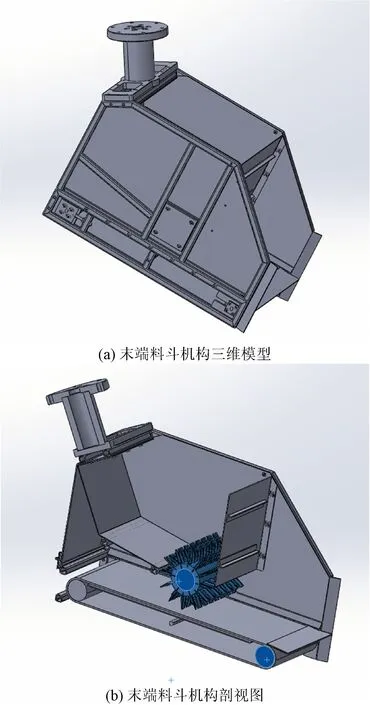
2.2 末端料斗机构流速控制

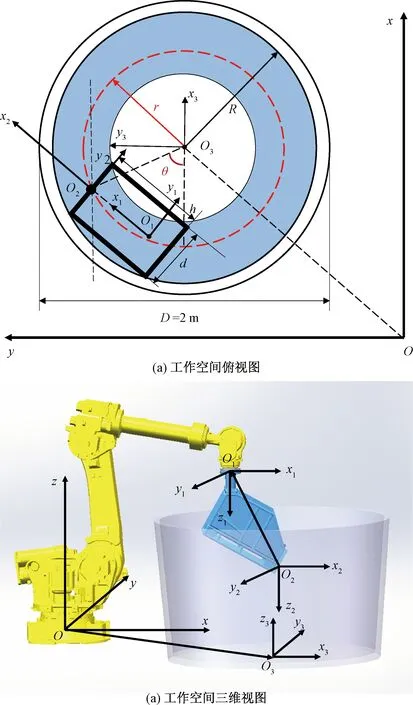
2.3 上甑轨迹规划



3 机器人上甑厚度控制策略
3.1 上甑机器人正逆运动学模型


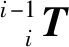



3.2 基于机器人动力学的机器人最大速度求解




3.3 给定厚度铺料控制策略


4 机器人上甑实验及数据分析


5 总结