高等教育与中国女性生育数量
朱 州,赵国昌
(西南财经大学 经济与管理研究院,四川 成都 610074)
一、引言
生育水平过低是当前和未来长时间内我国经济社会发展所面临的重大挑战。郭志刚和田思钰通过《中国人口与就业统计年鉴》的数据发现:我国育龄女性的总和生育率已经从1990年的2.3下降到了2015年的1.05,远远低于2.1的人口更替水平。[1]虽然Notestein 发现工业化和城市化发展会自然伴随着生育水平的下降,[2]但我国目前存在的最大问题是未富先老①实际上,世界银行数据显示我国老年抚养比(64岁以上人口与15-64岁人口之比)也超过了中高收入国家的平均水平。:在未完成工业化和现代化的条件下,生育水平的大幅下降导致我国提前步入老龄化社会。如图1 所示:从20 世纪90 年代中后期开始,我国的总和生育率不仅低于同收入类别的中高等收入国家(地区),而且还远低于高收入国家(地区)。2018 年中高等收入国家(地区)的平均生育水平在1.90,高收入国家(地区)的平均生育水平在1.60。2016 年全面放开二胎政策后,我国的总和生育率有了短暂上升,但2017 年、2018年的总和生育率也只有1.58、1.50。第七次人口普查数据显示2020年我国总和生育率只有1.3。由于新出生婴儿长成劳动力人口需要一定的时间,因此低生育率的当期和短期影响还会让劳动力人口占比上升,但其中、长期影响会导致人口老龄化。范硕和李俊江及蔡昉等人研究发现低生育水平会带来人口的老龄化,对经济社会的消费和储蓄、社会负担、人力资本投资、创新活力等方面都产生影响。引发人口红利消失、年轻人养老负担重、政府财政压力大、国内消费市场增长停滞等一系列的经济社会问题。[3-4]
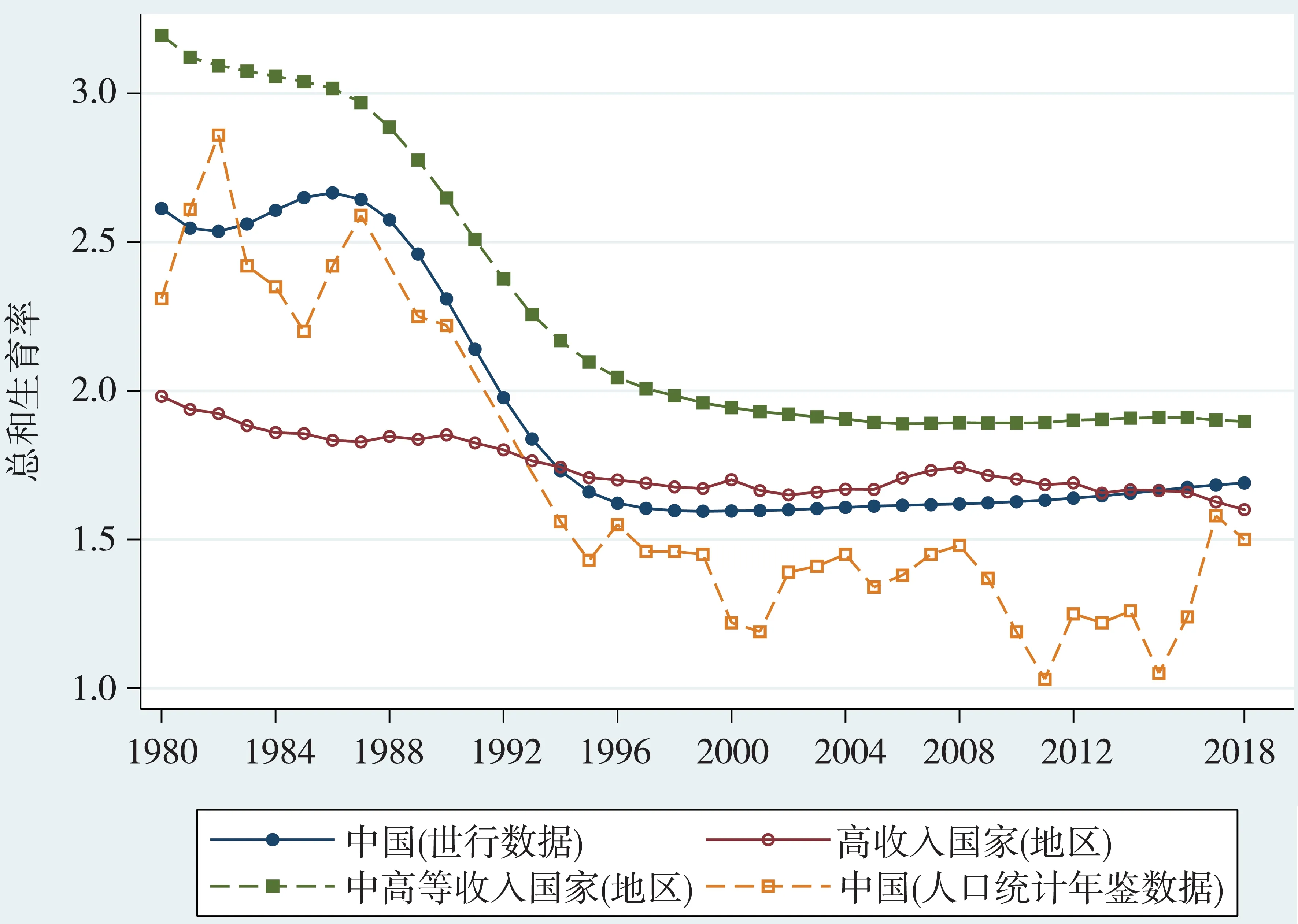
图1 中国与其他国家(地区)的生育水平比较
另一方面,20世纪90年代以来我国育龄女性中接受过高等教育的数量和比例持续大幅度上升。1990 年人口普查和2015 年1%人口抽样调查的数据显示:我国育龄妇女(20-49 岁)中大专及以上学历总人数由1990 年的397 万上升到2015 年的6 782 万,大专及以上学历占比从1990 年的2%上升到了2015 年的20.7%。《2019 年全国教育事业发展统计公报》显示2019 年我国女性的高等教育毛入学率已经达到了51%。实际上我国女性的大学毛入学率已高于男性。虽然目前社会和学术界有一些关于我国高等教育比例是否过高的讨论,但与同档次的中高收入国家(地区)相比,我国的高等教育人力资本积累并不占优势,只是近两年才达到平均水平,还远远低于高收入国家(地区)的平均水平(见图2)。为了让我国在未来全球竞争中拥有人力资本红利,最近公布的“十四五规划和2035 年远景目标纲要”就明确提出要将我国的高等教育毛入学率提高到60%。可以预期未来我国接近乃至超过一半的育龄女性将会接受高等教育。当前我国社会正处于婚育行为急剧变迁的阶段,生育水平的持续下降引起政府和社会的担忧:未来我国还会继续向着西方的少子化乃至丁克家庭模式变迁吗?高等教育女性作为西方婚育观念的率先接触者,她们的婚育行为是判断未来我国女性婚育行为模式变迁的风向标。那么,上大学是否会影响我国女性的生育数量?我国育龄女性中受过高等教育比例的不断提高是不是近年来我国生育水平下降的重要原因?在人口老龄化不断加剧的背景下,这两个问题的答案意义重大。要回答这些问题,需要准确估计出高等教育对于女性生育数量的影响。
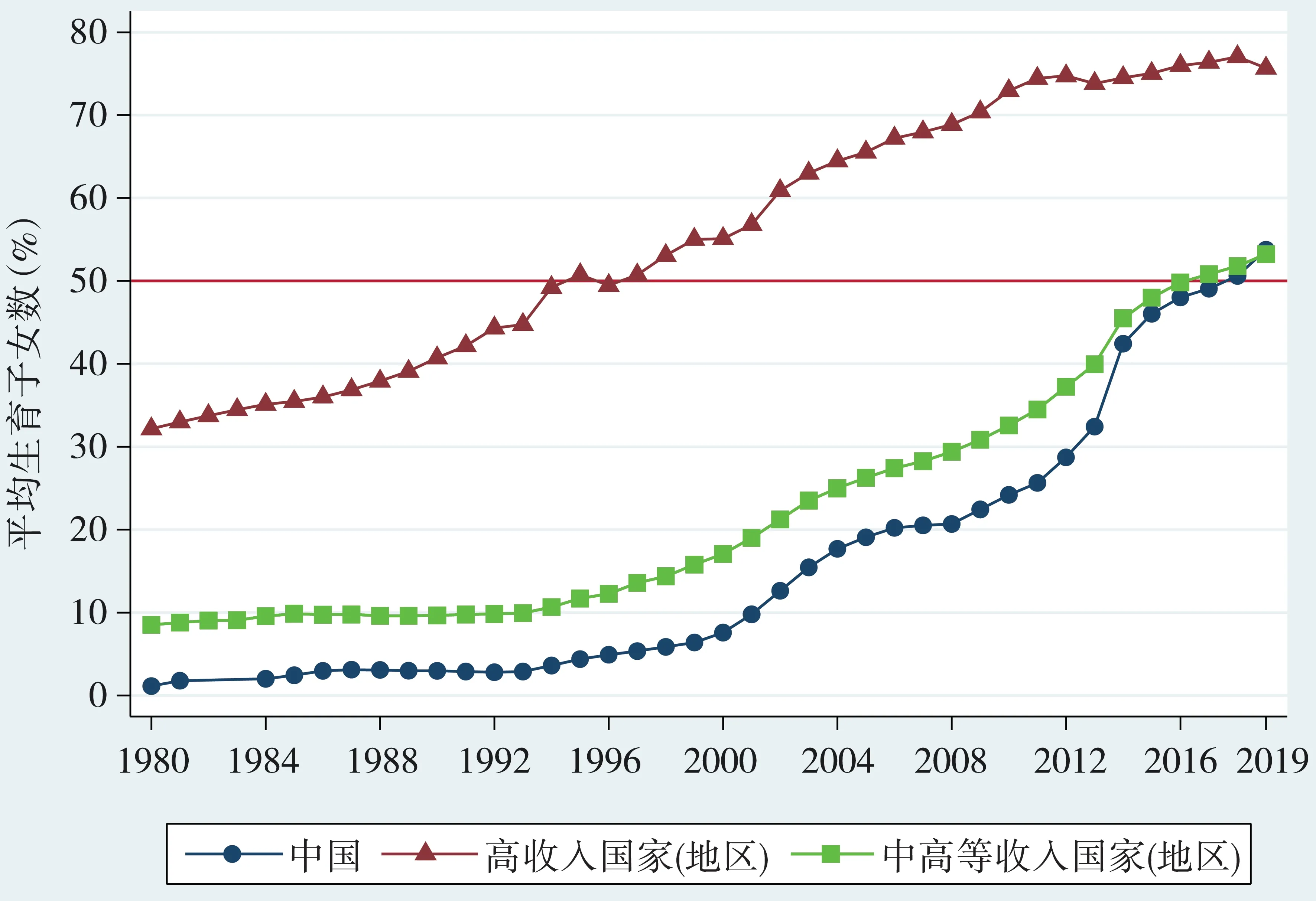
图2 中国与其他国家(地区)的高等教育总入学率比较
1990年以来我国女性总和生育率下降到更替水平以下,已经出现了很多关于女性生育水平下降原因的研究。梁同贵及薛君从人口流动、周长洪及陶涛等从经济社会发展、葛玉好和张雪梅从房价、郭志刚和田思钰从婚姻推迟等多种角度对我国生育水平下降进行了解释。[1][5-9]却少有文献实证分析教育因素在生育水平下降过程中的作用。作为重要的社会经济变量,Becker、Blossfeld 和Huinink 发现教育会通过劳动市场的(潜在的)收入效应和替代效应[10-11]或者通过禁闭效应等多种机制影响女性的生育数量。[12]从理论上来说,上大学会降低还是提高女性的生育水平并没有一致结论,因此相应的实证分析就非常必要。
虽然量化分析高等教育对我国女性生育水平的影响意义重大,但相关的实证文献还很少①近年来有少量学者开始关注教育对生育数量的影响,与本文类似的有杨振宇和张程的研究,他们用1986年义务教育法作为工具变量,发现因义务教育法而上初中的女性群体的生育水平下降了。[13]。一个可能的原因在于估计高等教育对女性生育数量的影响会同时面临内生性问题和生存数据结构问题。由于个人能力、事业心等不可观察的变量既影响女性的教育获得,也影响女性的生育数量,所以女性的受教育水平是内生的。本文既参照Duflo、Ou 和Zhao 及侯玉娜和邓宁莎等人的思路②Ou 和Zhao 在估计大学扩招政策的影响时,除了利用1999 年作为政策处理时间点,也用了各省高等教育扩张强度作为政策处理的地区差异。[15],[14-16]借助1999 年高校扩招政策强度在个人出生队列和户籍所在省份的双重外生差异,还利用各个省份本身的高等资源禀赋导致的高等教育入学机会差异来构造个人高等教育的工具变量。生存数据结构问题是指对于较为年轻的样本,调查截止时点观测到的生育数量不能代表该女性最终的生育数量。虽然可以通过把年轻女性样本删除的方式减弱这个问题,但这样做会让国内常见的微观数据库都面临样本量不足的问题。因为初步筛选的分析样本就只能是高中及以上学历③高中学历才适合做大学的参照组,这里的高中是指高中阶段,包括普通高中、中专、职业高中,下文同。,再排除较为年轻的女性样本,往往样本量非常小,很难保证在出生队列层面上的代表性。本文利用2015 年1%人口抽样调查的大样本数据,能够较为准确地描述高中和大学学历女性平均生育水平在不同年龄队列上的变动趋势。2015 年1%人口抽样调查的大样本能够帮助我们确定合理的起始分析年龄从而一定程度上克服生存分析问题。另外,结合翟振武和刘雯莉、朱州和赵国昌的发现,近年来我国各学历女性婚姻推迟明显而最终结婚率仍然很高。[17-18]将样本限定为已婚来消除因为婚姻推迟导致的暂时未生育的情况,可以进一步克服生存分析问题对估计结果的影响。
借助1999年高校扩招政策和各省高等教育资源禀赋所带来的高等教育机会在个人出生队列和户籍所在省份的双重外生差异,我们给女性能否上大学构造了一个工具变量来解决内生性问题,并使用IV-Poisson 模型估计了上大学对我国女性生育数量的影响。结果表明与高中学历的女性相比,上大学会使得女性生育数量平均下降30%左右。这种影响主要体现为上大学让女性生育二孩及多孩的概率大幅度下降,而并非不生。进一步分析发现上大学会通过提高女性的劳动市场参与率影响女性的生育数量,换言之高等教育提高了女性生育的机会成本。另外,本文还通过采用不同的样本起始年龄、用其他的工具变量以及用已育样本进行估计值下界(Lower bound)分析,结果都很稳健。根据本文的估计结果,育龄女性中高等教育比例的提高是20 世纪90 年代以来我国生育水平下降的重要原因。本文主要有三点贡献:第一,本文的研究结果有助于从高等教育发展的角度对1990年以来我国育龄女性生育水平的变动进行解释,并对我国未来的生育水平变动趋势进行展望。第二,上大学作为一种人力资本投资行为,传统文献多关注其对收入的影响。近些年以Oreopoulos和Salvanes为代表的一些文献开始关注教育带来的非货币化效应(Non-pecuniary effect)。[19]生育作为个体生命周期的重要节点,对家庭和社会的发展都具有极其重要的意义。本文发现上大学会显著地降低女性的生育数量,丰富了相关的文献。第三,在估计高等教育对生育数量的影响时,本文设计的识别策略对解决同类问题具有借鉴意义。比如用2015年1%人口抽样调查数据,通过描述我国高中和大学学历女性在不同年龄队列上的生育变动趋势,合理确定生育分析的起始分析年龄以克服所面临的生存数据结构问题。另外,本文用已育样本作为估计值下界(Lower bound)的稳健性分析思路也值得借鉴。
二、文献综述
作为重要的经济社会变量,教育可能会通过多种机制影响女性的生育数量。但从理论层面来说,教育到底会增加还是减少生育孩子数量是不确定的。首先,教育会通过提高女性在劳动市场上的(潜在)收入来影响生育数量:总效应取决于替代效应与收入效应的大小。替代效应是指教育水平更高的女性在劳动市场上的潜在收入更高,生育孩子所面临的机会成本更高。[10-11]因此,替代效应会使教育对女性生育数量产生负向影响。收入效应是指高等教育水平女性在劳动市场上的收入提高,使其更容易负担起养育小孩的费用,如果孩子是正常商品的话,会增加生育孩子的数量。另外,Behrman 和Rosenzweig 以及McCrary 和Royer 指出这种收入效应会因为婚姻的同质性匹配而增强,从而产生女性教育水平对家庭收入的乘数效应。[20-21]而Becker和Lewis则认为收入效应也会因为偏好孩子的质量而不是数量(Quantity-Quality tradeoff)而被削弱。[22]
其次,Grossman、Rosenzweig 等发现教育可能还会通过学习效应影响女性的生育数量:教育水平更高的女性往往掌握更多的避孕和生育健康方面的知识,或者是获取相关知识的能力更强,从而会更有效控制生育,因此主要是负向影响。[23-24]
再次,还有一些研究从婚姻机制和个人价值观念方面进行了分析。婚姻机制的影响是指在不存在非婚生子的情况下,教育水平通过影响结婚的可能性进而影响生育数量。一方面,Becker 发现教育可能降低女性的最终结婚率,[10][25-26]而Oppenheimer则发现教育也可能增加女性的结婚率。[27-29]还有一些研究比如Rindfuss 等认为教育水平会更多地给女性灌输一种非家庭角色的个人价值观,比如鼓励女性去追求个人的职业发展,在个人职业中实现自我价值等,从而影响女性的生育数量。[30]
最后,Black 认为由于现代教育都是在学校内集中进行的,因此教育会通过禁闭效应(Incarcera‑tion effect)推迟初育年龄、压缩可供生育的生理周期,从而降低生育数量。[12]而Monstad等研究这种负向影响后期可能会消失,高教育水平女性在毕业以后会进行生育追赶。[31]
翟振武、刘雯莉及朱州、赵国昌发现:在我国,相对于高中学历女性,接受过大学教育的女性虽然结婚要推迟,但仍然维持着非常高的终身结婚率。因此,婚姻机制的途径是不存在或者影响极小。[17-18]学习效应也应该不大,本文的对照组(高中学历的女性)基本的避孕和生育健康知识应该不会与接受过高等教育的女性有显著差异。因此在我国高等教育应该主要是通过收入或者价值观影响女性的生育数量。
近年来,陆续也有一些国外学者开始实证分析教育对生育数量的影响。但已有的实证研究也没有给出一致的结论。总的来说,在生育转型较慢、生育水平较高的发展中国家(地区)多发现负面影响,[32-33]在欧美等发达国家(地区)多发现没有影响甚至是正面影响。[21][34-35]但也有例外,比如Fort等发现教育水平的提高对英国女性的生育数量是负向影响,而在欧洲大陆国家则无负面影响。作者给出的解释是相对于欧洲大陆,英国的生育转型进行的更慢,而且市场提供的孩子照料服务和相关的政府政策并不太友好,从而降低了生育数量。[36]总的来说,教育对生育的影响受到生育转型水平、政府和市场对女性生育的友好程度等因素的影响。
就中国而言,目前我国并没有像北欧等国家一样提供让女性兼顾家庭和事业的环境,过去40多年的计划生育政策使我国大部分地区的育龄妇女已经提早完成了生育行为的转型,生育数量下降到极低水平。另外一方面我国目前仍然保有比较传统的婚育观念,我国女性的结婚率依然非常高,对于绝大多数家庭来说,至少生育一个孩子是普遍的观念,不育主义者所占比例还是非常小。在这样一个女性不容易平衡家庭与事业、又保有一定传统生育观念的发展中国家,研究高等教育对女性生育数量的影响就显得尤为必要。另外,20 世纪90 年代以来我国育龄女性中接受高等教育的比例快速上升,这一巨大的变化对我国的生育水平产生了怎样的影响,都需要相应的量化分析。[13][37]
虽然近年来也有少量学者开始关注教育对生育数量的影响,但要么仅限于简单的描述统计分析,要么研究集中于低学历群体,比如杨振宇、梁秋生等人的研究。[13][37]本文将借助于2015 年1%人口抽样调查的大样本数据,通过提高女性的起始分析年龄到30 岁以上的已婚样本来消除面临的生存数据结构问题;用1999 年高校扩招政策和各省高等教育资源禀赋所带来的高等教育入学机会在出生队列和省份上的双重外生差异构造高等教育的工具变量,用IV-Poisson 模型估计高等教育对我国女性生育数量的影响。
三、计量模型和识别策略
如前所述,在估计高等教育对女性生育数量的影响时会同时面临内生性问题与生存数据结构问题。职业理想、能力等遗漏变量会同时影响女性的教育和生育数量。本文参照Duflo、Ou以及侯玉娜和邓宁莎等人的思路①侯玉娜和邓宁莎也采用了Duflo的思想来构造各省高校扩招政策强度变量。与本文略有差异的是,其计算方式是1999年及以后各年该省当年普通高等教育招生人数与1998 年该省普通高等教育招生人数之差与当年该省高中毕业生人数之比。本文是直接计算的高等教育入学机会相比于1998年的增加值。,[14-16]借助1999 年高校扩招政策强度在个人出生队列和户籍所在省份的双重外生差异,同时还利用各个省份本身的高等资源禀赋导致的高等教育入学机会差异来构造个人高等教育的工具变量。其中各省历年的高等教育入学机会用各省当年普通高等学校招生人数与普通高中毕业生人数之比来衡量。在各省高考录取率数据缺失的情况下,这也是文献中的常用办法。个体受到的扩招政策强度是本文构造工具变量的关键。这既取决于个体参加高考的年份,还取决于参加高考时的户籍所在省份的扩招强度。本文用1999 年及以后各省历年高等教育入学机会减去该省1998年的对应数值,得到该年该省的高校扩招强度,并将1998年之前的扩招强度认定为0,构造出高校扩招政策强度变量。实际上,虽然1999年全国各省份都施行了大学扩招,但各省份在高等教育入学机会的扩招强度上存在较大的差异。根据本文的计算,扩招强度较小的西藏、宁夏、青海等省区,1999-2003 年高等教育入学机会年平均增加值在0.06~0.26 之间,而扩招强度较大的北京、天津等地则在0.35~0.67。因此,即便是同一队列的高中毕业生,因为户籍所在省份的差异,也可能会出现巨大的政策处理强度差异。在具体估计的时候,我们将构造出来的高校扩招政策强度变量及高考对应年份对应户籍省份的高等教育入学机会作为高等教育的工具变量解决面临的内生性问题②我们没有直接用扩招政策强度变量作为IV是因为目前还没有文献能够准确测量国内各省的高等教育入学机会。本文所用的各省当年高等院校入学人数与普通高中毕业生人数之比只是一个替代变量,会在一定程度上影响其作为工具变量的相关性。因此,在工具变量中还加入了各省当年高等院校入学人数与普通高中毕业生人数之比,作为各省存在的高等教育资源禀赋差异,有助于防止出现弱工具变量问题。。由于2015年1%人口抽样调查数据中并没有参加高考的年份信息,本文用其19岁时年份作为对应高考年份,这也符合我们的学制和前面的相关研究③本文用CFPS、CGSS中具有高考年龄信息的数据库都一致发现将高考年龄确定为19岁是更为合理的。。来自2015年1%人口抽样调查数据显示:从1980年出生队列开始,女性中大学占比出现跳跃性上升,说明将19岁时对应年份作为高考年份是合理的。另外,由于该数据中并没有给出参加高考时的户籍省份,本文用当前户籍所在省份进行代替④当然会有户口跨省份迁移的情况,但相对于全国的样本,占比较小,后面稳健性检验中有专门针对此问题的讨论。。
生存问题是指在观测时点,一些女性还比较年轻,这个时候即便观测到该女性没有生育孩子或者只有一个孩子,不代表以后终身都不会生育孩子或只有一个孩子。这也是当前国内生育相关的实证文献比较少的主要原因。除非样本中的所有女性都已度过生育窗口期,否则这个问题不能完全解决,但是通过对年龄进行一定的限制可以缓解这个问题。图3给出了2015年时20-40岁女性分年龄队列的平均生育变动情况。如图3所示,在假设各个相邻年龄队列的生育水平趋势具有一定可比性情况下,在30 岁及以前,随着年龄队列的上升,平均生育水平有较大幅度上升。而在年龄队列到达30 岁以后,这种上升幅度大大减小。到了33 岁时基本就稳定下来,随着年龄增加的幅度极小。因此,在实证分析中将只选用30 岁以上的样本,有助于克服生存分析问题。在稳健性分析中,我们还将起始年龄从31 岁上升到32 岁、33 岁,以尽量降低生存分析问题带来的影响。当然,我们也不能引入年龄太大的样本,这样会降低不同年龄出生队列所受政策差异的影响。因此最终本文将分析样本确定为31-40岁。
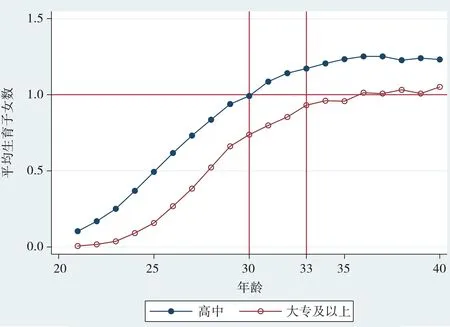
图3 高中和大学学历女性分年龄队列平均生育水平变动趋势
另外,本文还将分析样本进一步限定为已婚状态。主要是近年来我国婚姻推迟现象十分明显。另外一方面我国各学历女性的最终结婚率仍然很高。上大学只是延迟了女性的婚姻,并没有显著降低其最终结婚率。[17-18]婚姻机制在我国不存在或者影响极小。实际上,31-40岁的大学与高中学历女性在已婚状态上非常接近。31-40 岁大学学历女性目前处于已婚状态(排除未婚、离异和丧偶)的女性占比为90.04%,高中学历女性的对应占比为92.17%。两者差异仅在2%左右。在稳健性分析部分,我们将样本限定为33-40岁,该样本中,高中与大学学历女性的结婚率仅有1.44%的差异。而且本文也对全样本进行了分析,在控制住婚姻状态以后,估计系数基本一致。而婚姻推迟会导致暂时未生育情况,也会带来生存分析问题,[1]因此在基准样本中我们仅包括已婚女性。
传统上关于生育数量或者说生育率的研究多采用汇总数据,[38-40]但是这种方法不能控制个体微观特征上的差异。由于本文的被解释变量是生育数量,这是一个非负整数,普通的线性模型可能会存在一定的问题。而Poisson 回归作为一种计数模型,就是为了分析因变量是非负整数而出现的统计模型。[41]本文中的因变量(已生育小孩数量)恰恰属于这种类型,因此特别适合微观层面上对生育率的研究。[41]具体地,假设生育数量(N)i服从Poisson分布:

进一步地,Poisson回归假设:

由于在Poisson 分布中,E(Ni|λi)=λi,这意味着E(Ni|λi)=exp(γ'xi+πEdui)。如果教育程度采用受教育年限度量,则:

即100×π是如果教育程度增加1 年生育数量增加的百分比。如果教育程度用是否上大学的类别变量度量,则:
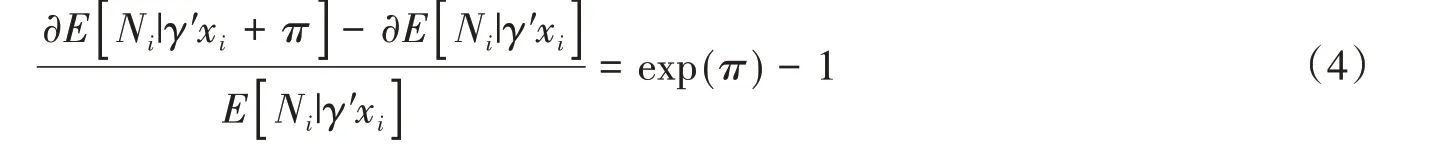
基于泰勒近似可知上式近似等于π,即相比于高中毕业生,大学毕业的女性的生育数量大约会增加100×π个百分比。
当我们在方程(2)中引入误差项ui,模型进一步扩展为:

如果ui与个人的教育程度相关,即E[ui|Edui]≠0,比如事业心强、能力强的女性的受教育程度会更高,同时也会选择生更少的孩子,此时E(Ni|λi) ≠exp(γ'xi+πEdui),并且Poisson 回归的估计是有偏的。与线性模型类似,这种情况下我们也需要为自变量寻找工具变量(记为zi),采用IV-Poisson模型来估计参数。此时工具变量需要满足的条件为:E(ui|zi)=0,该条件可以进一步写为:
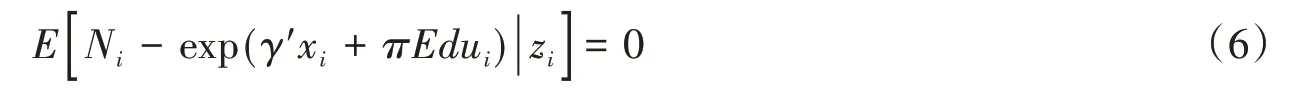
上述条件可以推导出如下的矩条件:[42-44]
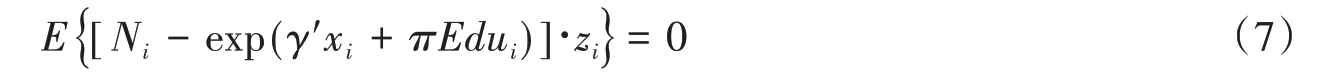
在本研究中,我们用高校扩招、各省高等教育资源差异以及二者交互项作为IV-Poisson 模型中教育程度的工具变量。
四、数据和变量
本文所用数据是2015年全国1%人口抽样调查个人微观样本数据。2015年全国1%人口抽样调查实际完成2 131 万样本,占全国总人口的1.55%。随机抽样了10%的个人微观样本提供给研究者使用。本文所用数据样本量为2 003 563①清华大学数据中心公开的是在总人口的1%样本基础上随机抽取10%形成的。本文所用的样本量更大。。接下来本文对样本进行了筛选。首先剔除了男性样本(剔除1 027 075 个,占总样本51.26%)。其次,为了解决面临的生存分析问题,我们只保留31-40 岁之间的女性样本(剔除832 610 个,占总样本41.6%)。这里剔除40 岁以上的样本是为了降低不同出生队列对生育行为的影响。另外,我们剔除了初中及以下学历样本(剔除93 598 个,占总样本的4.7%),是因为只有高中学历适合做大学学历的对照组。根据前面分析,本文还删除了婚姻状况缺失样本(占比0.1%)、户口登记地址缺失样本(占比0.003%),保留已婚样本(占比0.2%),最终剩下43 835个样本。
表1报告了主要变量的描述性统计结果。相对于高中样本,大专及以上女性平均生育子女数量要少0.24 个,约减少19%。如果只考虑已育样本的话,大专及以上女性的平均生育子女数比高中样本少0.22 个。说明样本中平均生育子女数量的差异主要不是来自大专及以上女性更多存在未生育情况。大专及以上样本的年龄要略低于高中及以上样本,这主要是因为1999 年扩招以来我国大学生的比例迅速增加。因此,越年轻的队列中大学生的比例越高。另外,在非农劳动比例上,上过大学的女性要显著高10个百分点,这说明上大学可能会通过劳动市场参与影响生育水平。
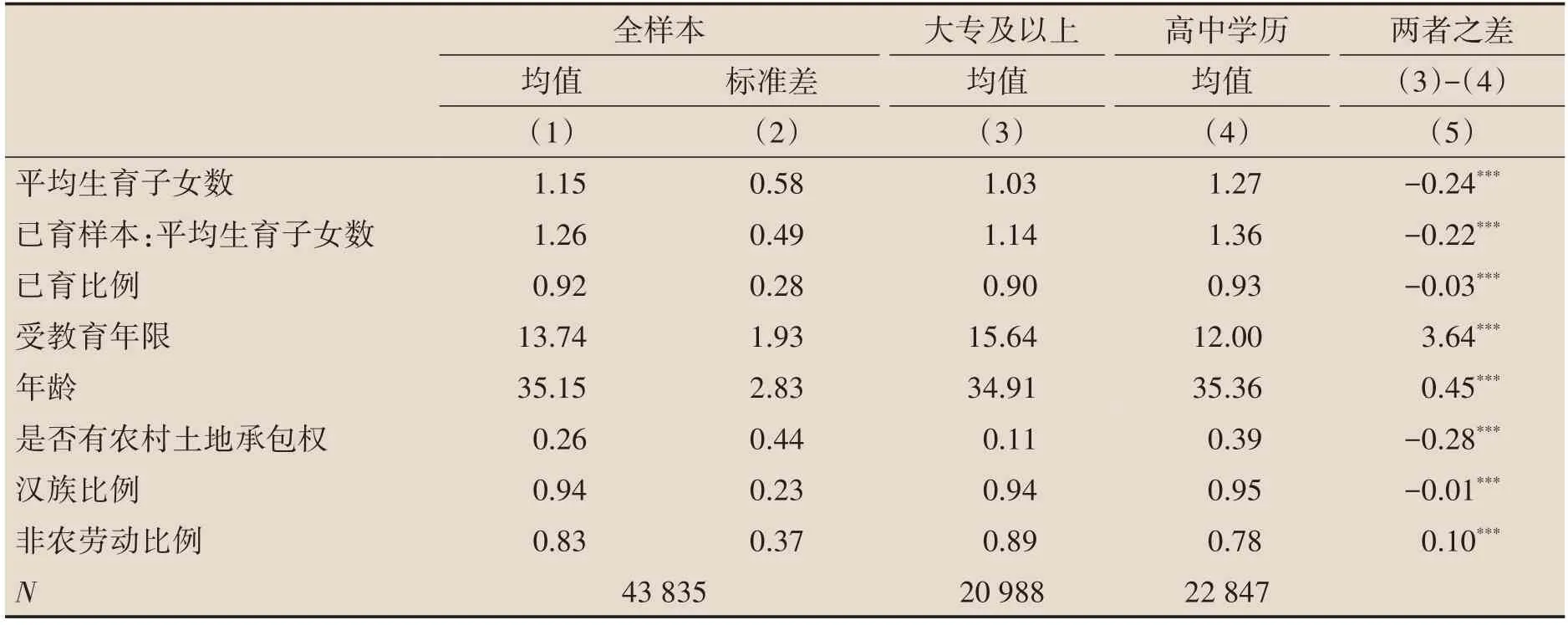
表1 主要变量的描述性统计
表2报告了生育数量分布的比较。在全样本中,仅有8%的女性还没有生育,可见本文通过将样本年龄控制在31-40岁并限定为已婚样本,有助于减轻删失数据结构带来的影响。约70%的女性生过一个孩子,22%的女性生过2个及以上的孩子。从表2还可以看出:大专及以上和高中学历的女性在生育数量分布上的差异主要体现为在生育二孩及多孩的比例上。在大专及以上教育程度的样本中,只有12%的女性育有2个及以上子女,而高中学历女性这一数值为30%。截至调查时点,这两种学历女性在是否已经生育上仅仅略有差异:在大专及以上教育程度的样本中,大约10%的女性还没有生育;而高中学历女性这一数值为7%,仅仅相差3 个百分点。总的来说,从表2 可以看出,大专及以上和高中学历女性在生育数量上的差异主要表现为少生,不生的差异较小。
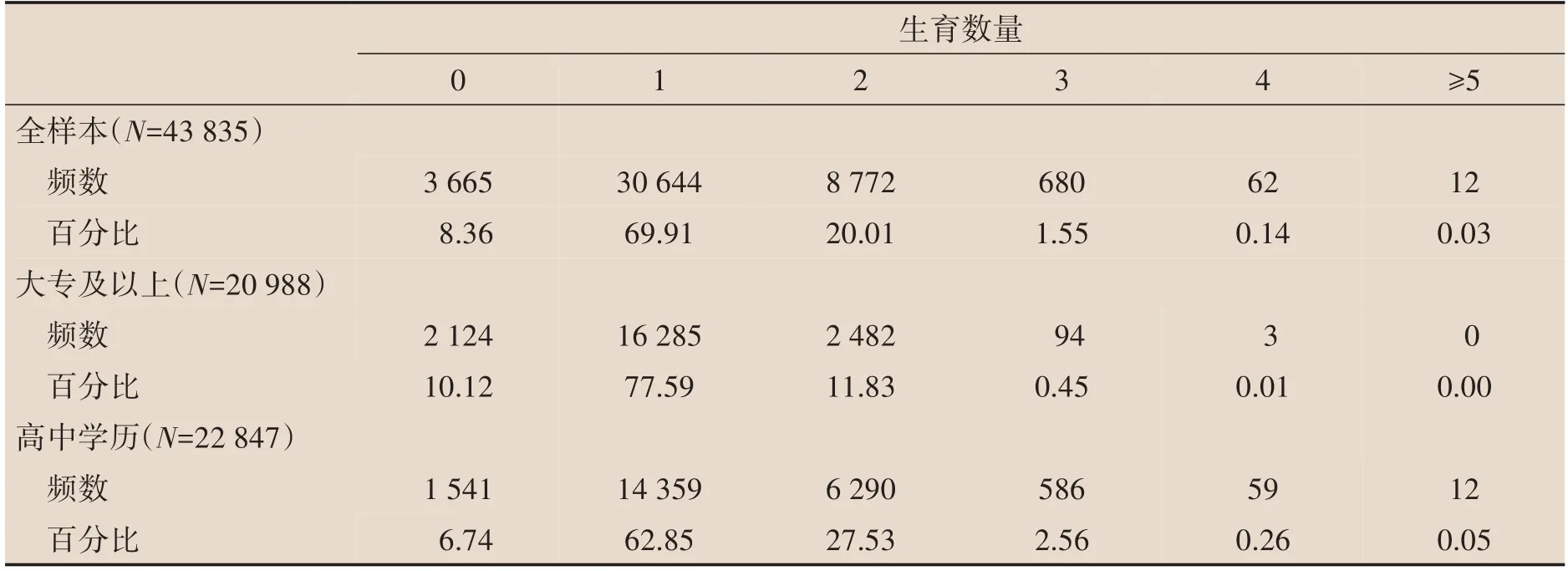
表2 生育数量分布比较
五、实证结果
1.高等教育对生育数量的影响
表3 给出了高等教育对生育数量的影响。其中第1、3 列分别是Poisson、IV-Poisson 模型的估计结果,第2、4列分别是OLS、2SLS模型的估计结果。由于OLS模型不适合本文的数据结构,其回归结果是不可信的。因此本文的所有分析都以Poisson 和IV-Poisson 模型为准。放入OLS和2SLS回归结果是为了与Poisson 和IV-Poisson 模型回归结果进行对比。正如前面所讨论的,这里将样本控制在31岁到40岁,共10个出生队列。既有助于减弱删失数据结构带来的影响,也能保证分析样本不掺杂过多队列,减少队列差异带来的影响。
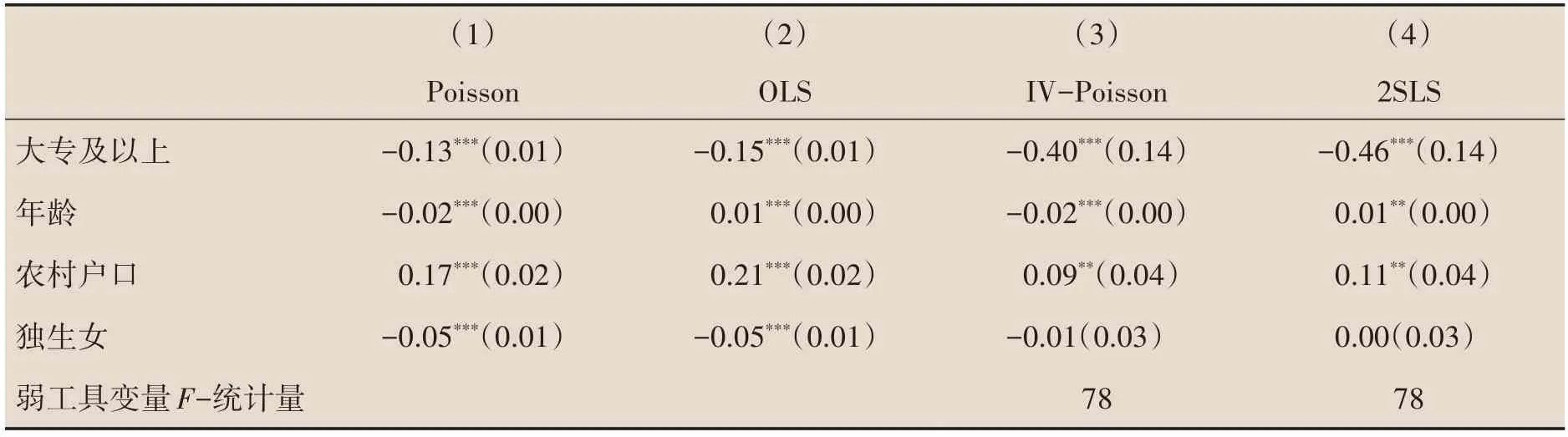
表3 上大学对女性生育数量的影响
从估计结果可以看到上大学确实显著降低了女性的生育数量。第1 列Poisson 模型的回归结果表明在不考虑内生性的情况下,相对于高中学历女性,上大学使得女性的生育数量显著降低13%。在考虑内生性问题后,第3 列IV-Poisson 模型的估计结果表明上大学使得女性的生育数量显著下降40%。本文的一阶段回归F值为78,说明我们的工具变量构造是有效的。通过对比第1 列与第2 列的结果,我们发现OLS模型比Poisson 模型估计出来的上大学对女性生育数量的负面影响要大,2SLS估计出来的负面影响也比IV-Poisson要大。回归结果也证实用OLS模型是不合适的。
2.稳健性分析
由于我们的估计系数对于解释和预测未来我国的生育变动趋势非常重要,有必要对系数进行更为准确的估计,为此我们进行了稳健性分析。进行稳健性分析的思路有三个方面:
第一,进一步提高样本起始分析年龄,降低生存数据结构问题对估计结果的影响。正如前面对图3 的分析:如果将分析样本的起始年龄从31 岁提高到32 岁、33 岁,有助于进一步降低生存数据结构问题对估计值的影响,有助于准确估计。第二,采用其他的工具变量进行稳健性分析。采用侯玉娜和邓宁莎构建高校扩招政策强度的方法。[16]在构建各省历年高等教育扩招强度变量时,不是计算高等教育入学机会的增加值,而是计算高中毕业生所获得的生均扩张名额。即将1999 年及以后该省高等教育招生名额减去1998年的名额,然后除以当年高中毕业生人数,并将1998年及以前的数值设定为0。从而构造出个体受到的高校扩招政策强度变量。在具体回归中将按照侯玉娜和邓宁莎的方法[16]计算出来的政策强度变量与高考对应省份当年高等教育入学机会作为高等教育的新工具变量(称为IV2,以前的称为IV1)。
两种稳健性分析的结果如表4 所示:其中第1、2、3 列是原来的工具变量(IV1)的估计结果,所分析样本是31-40 岁、32-40 岁、33-40 岁,而第4、5、6 列则是新的工具变量(IV2)的估计结果。所用模型都是IV-Poisson。从表4 的结果可以看出在将起始年龄提高和采用不同的工具变量后,估计结果仍然是稳健的。而且在将起始年龄提高到33 岁以后,我们最终的估计系数稳定在-0.3 左右。由于起始年龄设定为33岁,能进一步降低生存分析问题对估计系数的影响,因此本文把-0.3作为准确的估计值:即相对于高中毕业生,上大学让女性生育数量下降了30%左右。
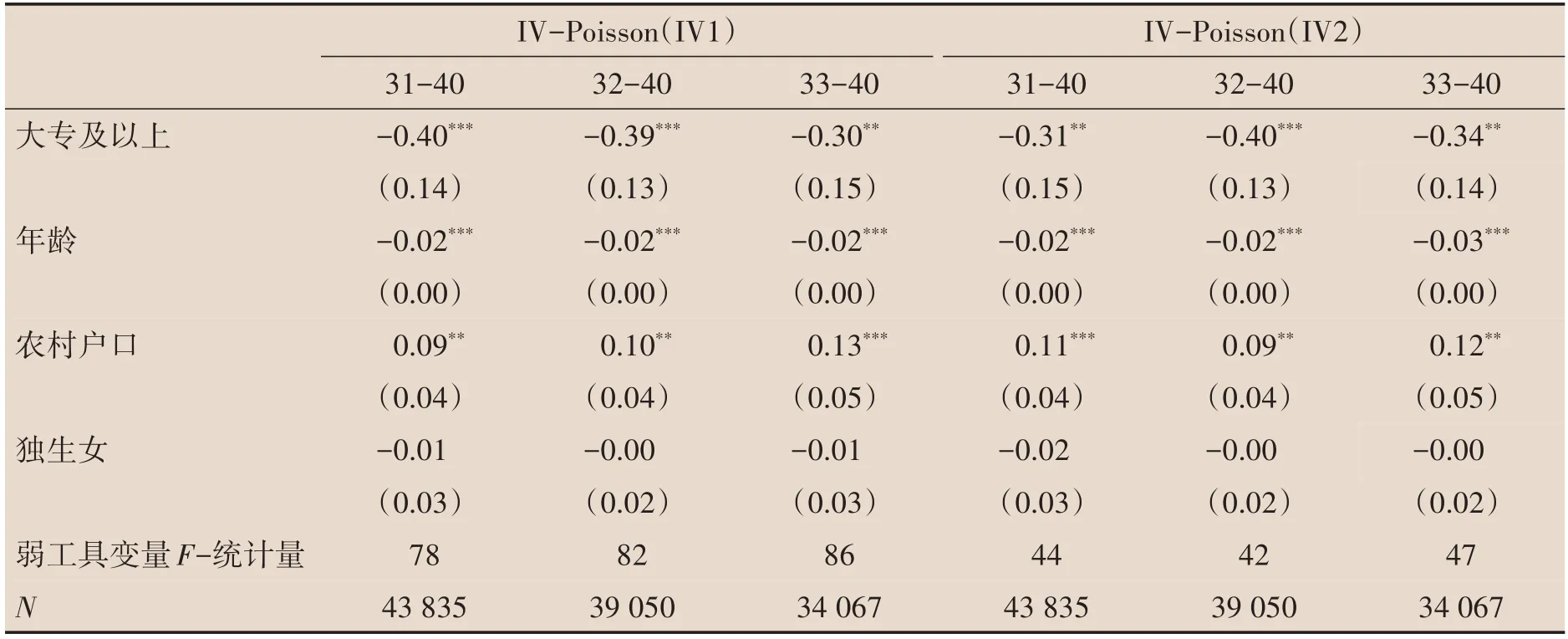
表4 上大学对女性生育数量影响的稳健性分析
虽然以上两种方式已经在保证工具变量有效性的前提下,受到扩招政策影响的第一代女性在2015年人口普查时最大年龄才35岁,尽可能地降低了生存分析问题带来的影响(起始分析年龄提高到33 岁),但很难说生存分析问题已经被完全消除。为了尽力排除这种担忧,本文还借助于另外一种稳健性分析的思路:采用下界(Lower bound)稳健性分析思路。具体做法是将分析样本限定为已育女性。根据基本理论和经验事实可以知道:大专及以上女性出于生育机会成本以及生育观念的原因,有更大的概率出现暂时或者终身生育为0 的情况,因此,当分析样本限定为已育样本时,对大专及以上女性的平均生育水平会有相对更大的提升效果,两种学历之间的生育差距会有所缩小。这点可以从前面表1 中得到证实:当采用已育样本时,大学与高中学历女性的平均生育数量差距从0.24下降到0.22。因此,采用已育女性样本所估计出来的效应应该要比前面的估计值要小,即相当于前面估计值的下界。如果估计值的下界是显著的,可以证明估计值本身是稳健的。
表5给出了用已育样本估计出的上大学对女性生育数量影响。表5的结果证实了我们前面的猜测。在将样本限定为已育女性后,估计系数绝对值为0.2左右,确实比前面对应的估计结果要小。从表5 的估计结果可以看到,即便估计出来的结果是影响效应(绝对值)的下界,这个效应也是显著为负的。从而证明我们前面的估计结果是稳健的:上大学确实显著地降低了我国女性的生育数量。
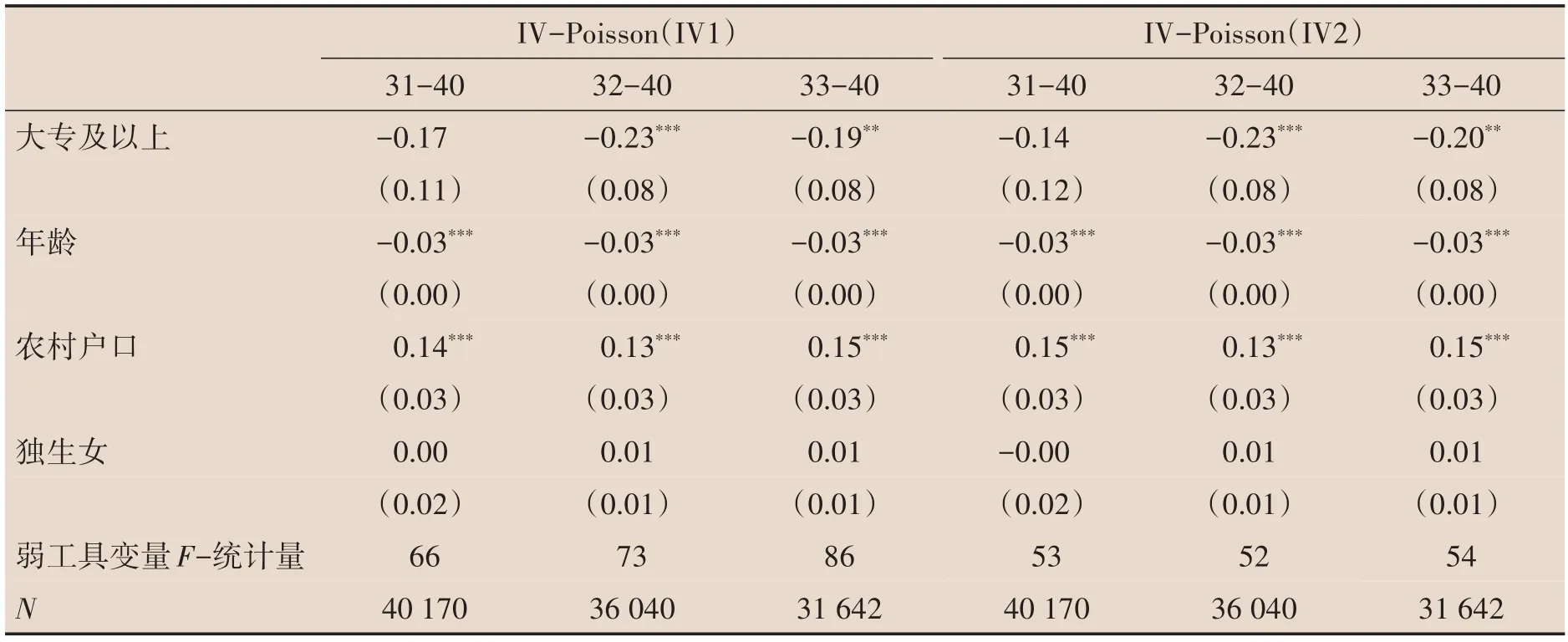
表5 上大学对女性生育数量影响的稳健性分析(已生育样本)
另外,本文用女性当前的户口所在省份作为其高考时的户口所在省份,可能会存在读完大学以后户口迁出的情况。也是就说要排除那些跨省流动概率较高的样本。为此,我们只保留在本地住满5 年的本地户籍人口或者在本地住满5 年的本省流动人口,这样来排除那些跨省流动概率较高的样本。在排除那些跨省流动概率相对较大的样本后,本文的估计结果仍然是稳健的(限于篇幅,此处未展示)。
3.上大学让女性不生还是少生?
前面的实证分析结果表明上大学确实能显著降低我国女性的生育数量。那么这种差异主要表现为不生还是少生?具体来说上大学对生育数量的负面影响是表现为不生育概率更高?还是会进入生育但生育二孩及多孩的概率更低?为此,表6 给出了上大学对女性不生育子女以及生育二孩及多孩概率(限定为已进入生育样本)的影响。由于Stata 中IV-Probit 命令不适合离散内生变量,而OLS 和2SLS 同样可以获得系数的一致估计。因此,表6 给出了OLS 和2SLS 的估计结果。从估计系数来看,上大学让女性不生育的概率增加了15%,但不显著。而上大学让已育女性选择生育二孩及多孩的概率显著下降23%。即上大学会显著降低步入生育女性选择生育二孩及多孩的概率。在我们将样本的起始年龄提高到32 岁、33 岁后,上大学对不生育概率的估计系数下降到0.05 且依然不显著;上大学对生育二孩及多孩的概率的影响系数仍为20%左右,而且在1%水平上显著(限于篇幅,此处未展示)。可以说,上大学对女性生育的负面影响主要体现为少生,而并非不生。这也与前面表2的描述统计结果相符。
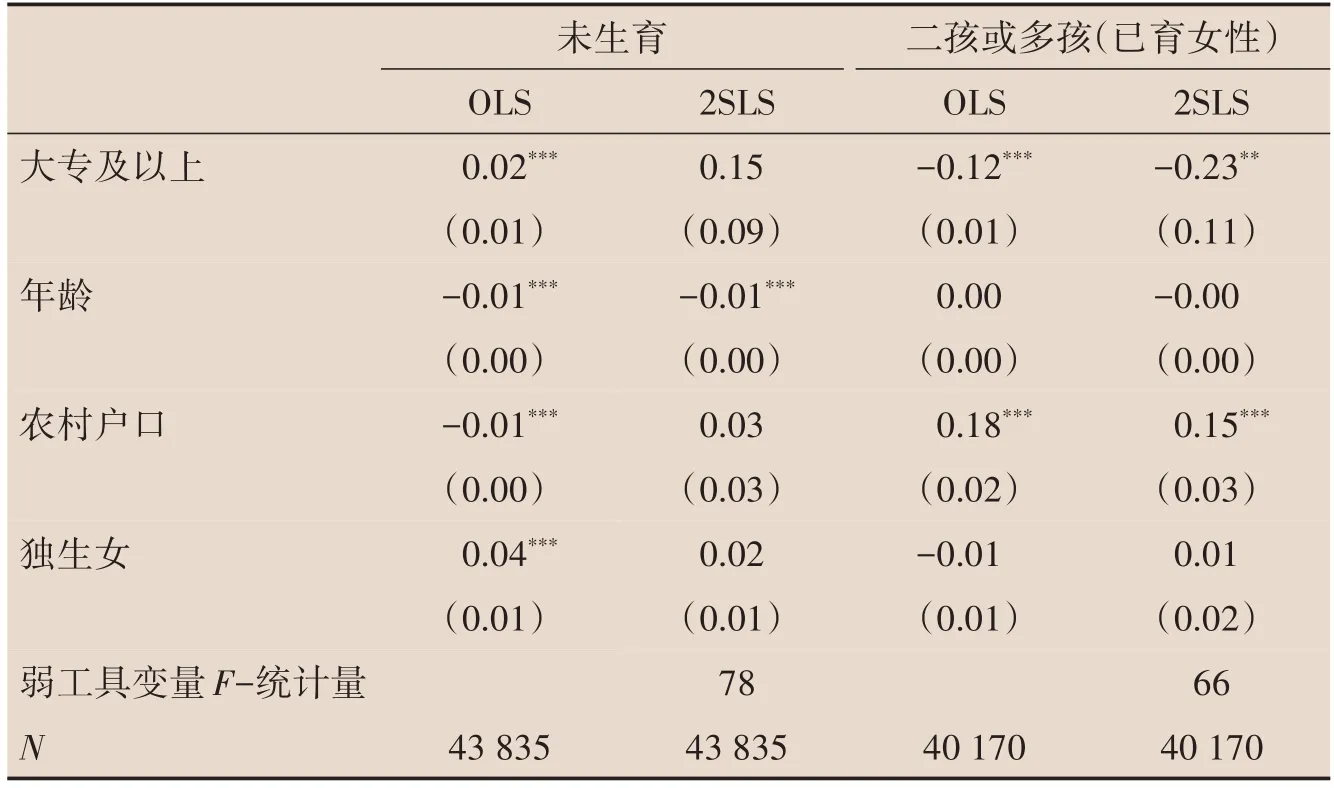
表6 上大学对女性不生和少生概率的影响
4.机制分析
根据前面的分析,在我国上大学主要会通过机会成本、改变女性价值观念等机制影响女性的生育数量。2015年人口小普查数据询问了女性劳动市场参与情况。与以往研究的结果类似,本文也发现上大学显著提高了女性的劳动参与率(限于篇幅,此处未展示)。更高的劳动参与率意味着高等教育女性生育小孩的机会成本更高。在当下的中国劳动市场,缺乏足够的让职场女性更好地平衡事业发展与家庭照料的政策支持。构建生育友好型社会可能有助于缩小高等教育女性与高中学历女性的生育水平差异。
5.小结
总的来说,前面的分析发现女性接受高等教育确实会显著降低生育数量。背后的机制包括上大学会提高女性的劳动参与的概率,这主要体现为生育的机会成本机制。当然还可能存在价值观念等机制,比如上大学对女性生育数量的负面影响主要体现为少生,这与传统的多子多福的观念是不同的,但基于现有数据我们无法进一步探讨其他可能的影响机制。
六、结论
1990年以来我国育龄女性的总和生育率持续下降,目前我国生育数量已远低于更替水平。与此同时,我国育龄女性中接受过高等教育的比例持续提高。本文尝试从高等教育角度对20 世纪90 年代以来我国生育数量的转变进行解释。借助于1999年高校扩招政策和各省高等教育资源禀赋带来的高等教育机会在出生队列和区域上的双重外生差异,构造了高等教育的工具变量,并通过将分析样本限定为30岁以上的已婚女性来克服面临的生存数据结构问题,并使用IV-Poisson模型量化分析了高等教育对生育小孩数量的影响。估计结果显示女性上大学对生育数量有显著的负面影响。相对于高中学历女性,上大学使得女性的生育数量平均下降30%左右。而且这种负面影响主要体现为让女性生育二孩及多孩的概率大幅下降,即让女性少生而非不生。本文发现上大学会通过提高女性劳动市场参与率这种机制影响女性的生育数量。
那么,如何看待我们的估计结果?首先,高校扩招导致的我国育龄女性队列中的高等教育比例提高是近年来我国生育水平下降的重要原因。根据IV-Poisson 模型的估计结果,上大学使得女性的生育数量平均下降30%左右。在全面二孩政策已经全面实施,计划生育政策已经不再是阻碍我国生育水平的重要因素的条件下,育龄女性中接受高等教育比例的大幅上升会成为导致我国生育水平下降的最重要因素之一。其次,要准确量化分析上大学对生育数量的影响,需要同时考虑内生性问题和生存数据结构问题。要解决这两个问题,需要使用个人微观大样本数据。对于内生性问题,现有文献多用1999年开始的高校扩招来解决,但这要求分析样本中有一定比例扩招后参加高考的样本,但并非所有受到扩招影响的样本都可以包括进来。在分析的时候,要根据我国不同年龄队列女性的平均生育变动趋势合理确定样本起始分析年龄,既保证有足够多的受到扩招政策影响的样本(工具变量的有效性),又能尽量降低生存数据结构问题对估计结果的影响。
本文的贡献有三点:第一,本文对高等教育影响女性生育率的量化分析,有助于从高等教育发展的角度理解20 世纪90 年代以来我国生育水平的变动趋势。第二,以往传统的关于高等教育的文献多关注教育带来的货币收益,近年来有少量文献开始关注教育产生的非货币收益,本文通过探究上大学对生育数量的影响丰富了这类文献。第三,本文用2015年人口小普查个人样本数据的大样本,通过控制所用年龄队列,大大降低生存数据结构问题带来的影响。当然本文还存在着一些不足之处,比如由于没有被访者关于婚育价值观念、个人收入等方面的信息,无法对影响机制做全面的分析。
总的来说,在女性生育行为模式上,我国与发达国家(地区)既有相同点也有不同点:相同点是都完成了初育推迟、生育数量低于更替水平的生育转型。不同点在于:在我国传统生育观念依然发挥着比较大的影响,已婚家庭对生育一个孩子的需求依然很高,终身不婚不育的女性比例很低,这可能是我国相对于欧美国家存在的生育潜力。本文发现高等教育确实是造成生育数量下降的重要原因。女性教育水平的提高绝对是社会进步的推动因素,而且我们也会预期到中国女性的教育水平会进一步提高。因此,进一步研究高教育程度的女性生育时面对哪些成本和顾虑,只有了解她们对孩子的需求,才能推出更有针对性地缓解我国生育率下降的政策。

