基于非结构化网格的复杂构造建模方法研究——以四川双鱼石地区为例

兰雪梅，张连进，徐 伟，蒲柏宇，王俊杰，王天琪

(西南油气田公司勘探开发研究院，四川 成都 610041)

0 引 言

我国西部地区位于印度板块与欧亚板块交界处，地质构造极其发育。区域上大型断裂与伴生断层发育，断层之间相互截断、相交等空间组合关系复杂，利用常规勘探方法准确断面组合难度大，交切关系计算困难[1-3]。同时，大断距、高幅度、窄条幅及复杂的断层组合样式，对网格剖分造成极大难度，导致网格形变严重、正交性差，影响后续数值模拟的速度和精度[4-7]。随着地质建模技术不断发展，构造建模和裂缝建模技术也不断向复杂化、精细化与大规模化推进[8-10]。

常规数值软件对复杂地质条件下的建模结果通常存在地层网格非常扭曲，导致层面模型不准确；出现大量的负网格、体积异常大网格；Petrel IJ网格编号不准确；针对有凹凸起伏、断面形态变化比较大的断层，很难完全拟合断层面[11-12]，即使是经过平滑处理的断层面都很难拟合；若通过增加控制点的个数来拟合断层面，又会大幅增加人工交互的工作量[13-16]；针对复杂的断层交切关系，通过编辑得到的断层交线与实际的断层交线差别较大。常规方法在构建地质模型时存在的问题会影响后续的属性建模、储量计算和数值模拟工作[17-19]。基于此，选择非结构化网格，利用petrel软件建立地质模型，根据地震数据基于属性插值方法，加载井口数据及地层参数，对双鱼石地区复杂构造进行建模，有效获取地质岩体及构造发育特征。

1 Petrel建模方法

1.1 弱化相交网格剖分方法

双鱼石区块主要位于四川省广元市剑阁县昭化区及利州区境内，构造单元上隶属上扬子克拉通北缘龙门山山前褶皱带，西邻龙门山逆掩推覆带，东接川北古中坳陷低缓区。由于受逆冲推覆挤压作用，整体褶皱变形、断裂发育，形成一系列呈北东南西向展布、近平行的褶皱断高构造群。工区内断块宽度为1～3 km、构造幅度50～550 m、断层断距80～300 m、断层搭配样式复杂(图1)，对区域上大断距、高幅度、窄条带的构造建模难度大，需通过petrel构造建模技术更好地刻画双鱼石地区构造特征。

图1 双鱼石地区地质构造地震剖面

采用非结构化网格对复杂构造进行精细表征，首先需要提取复杂构造的几何信息，以这些几何体为约束进行非结构化网格剖分。若断层等构造几何体十分复杂，采用结构化网格剖分，会造成网格数量巨大，且容易产生大量“病态三角形”[13,18-21]，导致网格整体质量变差，计算不稳定，甚至不收敛，这也是目前制约非结构化网格技术大规模商业应用的主要原因之一。

为了处理双鱼石地区广泛存在的高角度复杂缝网，同时保留薄层分层信息，发展了三棱柱层状非结构化网格，其同样基于Delaunay三角形剖分，通过空间仿射变换进行三维网格重构，并还原三维离散裂缝(图2)。基于“复杂曲面弱化求交”算法，距离和夹角简化断层等构造几何体的复杂度，消除病态三角形，形成高性能非结构化网格剖分方法，实现了任意复杂缝网条件下的非结构化网格剖分(图3)。

图2 三棱柱网格剖分流程

图3 复杂曲面弱化求交法[3]

1.2 非结构化网格下的属性插值方法

非结构化网格中，性质最优的、最适合用于油藏数值模拟的有三棱柱网格和四面体网格(图4和图5)，这2种网格在网格灵活度、复杂断层、裂缝表征精确度、地层信息描述以及数值计算收敛型等方面各有所长。主要通过2个技术来实现：优化搜索策略，仿照非结构化网格传导率连通表技术，提前形成网格节点距离连通表，与传导率联通表不同的是，距离联通表的连通系数为2个网格中心点距离；发展并行算法，每个网格的属性插值计算过程是独立实现，提高非结构化网格插值效率数十倍，建模时间与结构化网格相近。

图4 三棱柱网格化模型

图5 四面体网格化模型

非结构化网格针对高角度构造主要通过三棱柱网格及四面体网格进行划分。三棱柱网格在进行非结构化网格时能有效保留构造层信息、构造正交性良好，适合处理高角度裂缝、断层、薄层模型；四面体网格具有网格化灵活、断层、裂缝精细表征，适合处理复杂断层、裂缝网络。

1.3 非结构化网格的传导率处理与连通表征技术

网格的传导率与渗透率类似，通常认为是与流体性质无关的属性，为简单起见，笔者所有讨论均假设为单相流动问题且忽略重力影响。对任意控制体，流量公式可以表示如下：

Qi,j=Ti,jλ(pi-pj)

(1)

式中：Qi,j为单位时间中从网格块i到网格块j的流量；pi、pj为网格块压力；Ti,j为传导率，只与网格和多孔介质属性有关；λ为流度，和流体属性有关。

利用petrel对地质体数据网格剖分完毕之后，最重要的问题就是解决裂缝基质网格之间的传导率。离散裂缝模型的传导率计算可分为基质-基质(M-M)传导率、基质-裂缝(M-F)传导率和裂缝-裂缝(F-F)传导率，如图6所示。

图6 三维离散裂缝模三种传导率示意[5]

1)基质-基质(M-M)传导率。假设在每个网格内部，压力梯度方向沿着网格控制点与公共边(或公共面)形心连线的方向[13-14]，则由流量守恒得：

(2)

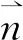
于是得到任意形状的基质网格间传导率的T1，2可通过下式进行计算：

(3)

2)基质-裂缝(M-F)传导率。在计算传导率的时候，裂缝会被还原成原来的形态，因此基质-裂缝的传导率计算与基质-基质的传导率计算是完全一致的，只是式(3)中的αf变为

αf=Afkf/Di

(4)

3)裂缝-裂缝(F-F)传导率。通常针对裂缝-裂缝模型构建过程中，地质体中2个裂缝网格之间不存在公共面，无法直接使用式(2)进行计算[11,17-18]。为解决公共面不存在的问题，引入体积无穷小的虚拟网格“0网格”进行计算。“0网格”的特点是与相连两条裂缝都是“正交”连接的，即网格中心点连线0-1和0-2分别与其公共面正交。我们的假设是裂缝网格1到裂缝网格2发生的所有流动都是通过“0网格”传导的。因此有：

(5)

式中：Bi为网格i与网格0交面面积，即裂缝网格i的宽度；mi为裂缝网格渗透率。

由于“0网格”为设定为无穷小，即有：

(6)

因此：

(7)

当裂缝出现相交(包括分支、汇合等)情况的时候，会出现3条及以上相交裂缝网格间的传导率计算。与i类似，也在交点处加入“0网格”。

由于在网格中裂缝用线段表示，而在计算模型中考虑了裂缝的宽度，因此会引起总体积不守恒。当裂缝较多的情况下，这种误差就不能忽略。处理的方法是对和裂缝相邻的基质网格做体积修正，即计算基质网格体积时(计算传导率时只用到了中心点和交面的信息，无须修正)要从中减去与之相邻的裂缝网格体积的一半(图7)。

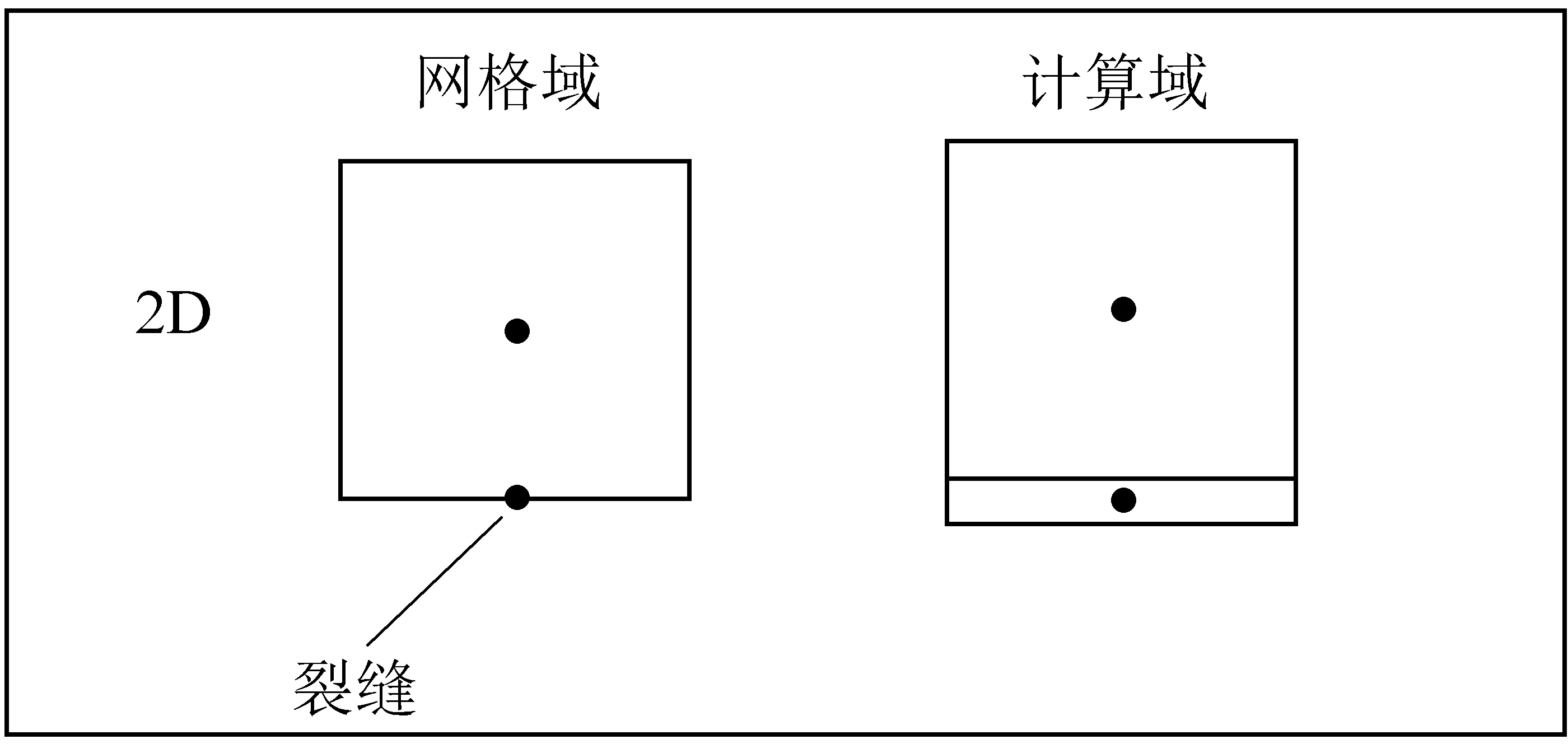
图7 计算模型与网格模型中裂缝网格的区别[9]

2 复杂构造的三维地质网格模型特征

2.1 建模区域

基于非结构化网格，选择双鱼石地区东北部区域(图8)，建立三维地质网络模型，构建地层特征。

建模区域面积533 km2，该区域囊括了区块最复杂的断层样式及接触关系；建模层位：茅口组、栖霞组断层，区域共有大小断层52条，分别采用常规pillar和自由断面组合2种方法建模；选取3种网格进行三维地质建模，常规角点网格、三棱柱网格、四面体网格；网格设置中角点网格大小为100×100×10，总网格量160万；三棱柱网格大小为平面约50 m，垂向10 m，剖分困难；四面体网格大小为约50 m，总网格量约148万。

沉积相及属性建模过程中由于角点网格剖分质量太差，所以选择在四面体网格的基础上进行沉积相及属性建模，基于沉积相平面图进行确定性沉积相建模，基于井上的测井数据及平面图，进行约束性的序贯高斯属性模拟。

2.2 三角剖分的复杂断层模型

进行三角剖分时，对双鱼石地区使用Delaunay三角剖分表征断层面的几何形态，建立不依赖于pillar的断层面描述方法，能精确的表征弯曲的断层面；复杂断面自动求交，操作简单，提高效率，不受断面形态的影响，精确度高(图9)。

图9 三角剖分断层结构

基于复杂断层模型进行非结构化四面体网格剖分；剖分的网格质量高，体积均匀，不会有大量扭曲。结果表明，双鱼石地区断层主要以大角度逆冲断层形式产出，断裂延伸长度大，区域大断层伴生有大量的小型断裂(图10)。通过三角剖分技术，可以清楚的显示出双鱼石地区的断裂形态。

在剖分的非结构化网格基础上，基于井上的孔隙度、渗透率曲线，利用序贯高斯模拟方法，建立孔隙度、渗透率模型；由于工区的井比较少，所以利用储层厚度图对模型做平面趋势约束；进行渗透率建模时，把孔隙度模型作为约束体，进行协同建模，建立渗透率模型(图11)。

图11 双鱼石地区地层渗透率分布特征

通过建立孔隙度、渗透率模型，双鱼石地区总体渗透率为0.11%～7.49%，平均渗透率为2.09%。茅口组渗透率为0.11%～7.49%，平均渗透率为2.39%；栖霞组渗透率为0.16%～3.20%，平均渗透率为1.49%。双鱼石地区总体孔隙度为0.01～1.052，平均孔隙度为0.26。茅口组孔隙度为0.01～1.069，平均孔隙度为0.32；栖霞组孔隙度为0.020 0～1.183 7，平均孔隙度为0.139 9。总体上双鱼石地区茅口组与栖霞组渗透率与孔隙度较小，属于致密岩层，不同区域上岩层孔隙度与渗透率有一定程度的变化，西南部渗透率略微高于东北部区域。

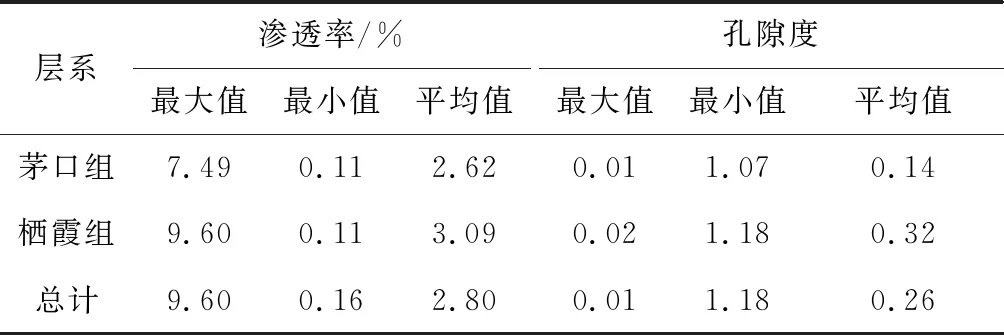
表1 双鱼石地区渗透率及孔隙度特征分布

3 结 论

1)基于petrel建模软件，优化地质构造建模方法，针对获取的地球物理数据提出弱化相交网格剖分方法与非结构化网格法，对复杂构造区高陡构造的地质建模有较好的效果，将该方法运用于四川盆地双鱼石地区，直观有效解释了双鱼石地区断裂构造空间展布特征。

2)利用非结构网格法下的属性插值，建立三角剖分的复杂断层模型，恢复了双鱼石地区主要目标岩层茅口组与栖霞组的地层特征，对断裂切割地层的方式与组合特征有效恢复，区域上结合渗透率和孔隙度模型，得到双鱼石地区渗透率与孔隙度平面分布特征。

3)孔隙度与渗透率模型计算结果表明，双鱼石地区总体渗透率为0.11%～7.49%，平均渗透率为2.09%；孔隙度为0.01～1.052，平均孔隙度为0.26。总体上双鱼石地区茅口组与栖霞组渗透率与孔隙度较小，属于致密岩层，不同区域上岩层孔隙度与渗透率有一定程度的变化，西南部渗透率略微高于东北部区域。