多轴并联机器正运动分析与视觉伺服研究

孙 娜，王 强，赖淑惠

（1.宁夏理工学院，宁夏 石嘴山 753000；2.陕西科技大学，陕西 西安 710021）

1 引言

在工业生产中，快速抓取和精准装配等任务需要消耗大量的人力和物力。为了完成工作，并联机器人必须将一些特定的工具装配在手臂上，以实现小范围内的快速任务操作。与其他类型的机器人相比，并行机器人是一种非常简单且易于制造的机构，其重量轻，功耗低，自治性也是值得考虑的有趣因素[1-3]。六轴并联机器人是一种具有高载荷自重比的封闭式运动结构，其适用于制造、飞行仿真系统和医疗机器人等领域。机械手是一组运动连杆或链条的集合，这些连杆或链条连接在一起形成一个能够完成特定任务的机构[4]。机器人具有串联和并联两种基本设计，在运动学上有明显不同。虽然串行机械手的运动结构是开环且更易于理解，但不适用于快速分拣、小范围搬运等场合。六轴并联机器人是一种闭环运动结构，逆运动学求解容易，但正运动学相对较难。1947年，并行机器人的设计思想被首次提出，Stewart基于他的并行模型建造了飞行模拟器。Clavel于1989年提出了Delta结构，这是一种专用于高速应用环境的并行机器人，其并联操纵器具有高精度定位和定向的特点，使其成为许多应用的理想解决方案，目前已在工业中得到广泛使用。

研究了6轴并行机器人的机械结构和运动特性，其工作空间是一组点集。首先，介绍了并联机器人的设计和运动学建模，利用牛顿修正优化算法求解了正向运动学。再次，根据图像学形态特征开发了从图像信息中确定待抓取目标的图形特征，然后设计分拣抓取的功能模块。最后利用实验验证了六轴并联机器人运动学和视觉抓取模型的正确性，为后续六轴并联机器人快速分拣提供了保障。

2 机器人结构与系统

2.1 机械臂结构

并行机器人已成为机器人领域的一大热点，与串行机器人相比，并行机器人在其整个工作空间中具有更大的负载能力，运动更快更准确，刚度也更大的特点，因此并行机器人的并行操纵器能够执行高精度的定位任务。六轴并联机器人机械结构，平行结构固有地通过致动器分配扭矩，使机器人具有高带宽动态特性，如图1所示。机器人本体采用六联杆并联驱动结构，主要包括用于机器人及电机固定的安装固定座，带有绝对编码器和制动器的六个伺服直驱电机，用于传递电机驱动力六组连杆驱动机构。

图1 六轴并联机器人机械结构Fig.1 Mechanical Structure of Six-Axis Parallel Robot

与串行机器人相比，并行机器人可提供更高的动态能力，更高的刚度、承载能力和定位重复性。这些与并行机器人相关联的属性使它们在实际应用中具有很大的吸引力。六轴并联机器人如何实现在自动装配、快速分拣、高自重比和高精密机械加工中发挥作用就显得尤为重要。

2.2 机器人系统

本研究使用了LabVIEW ver.7.1作为控制软件[14]。以Vision Assistant 7.1 作为前端图像处理软件，将Vision Assistant 生成的图像处理程序构建在LabVIEW上进行集成应用[15-16]。控制系统由末端执行器控制、图像处理、机器人载体控制和中央控制单元四部分组成，并联机器人系统程序架构，如图2所示。

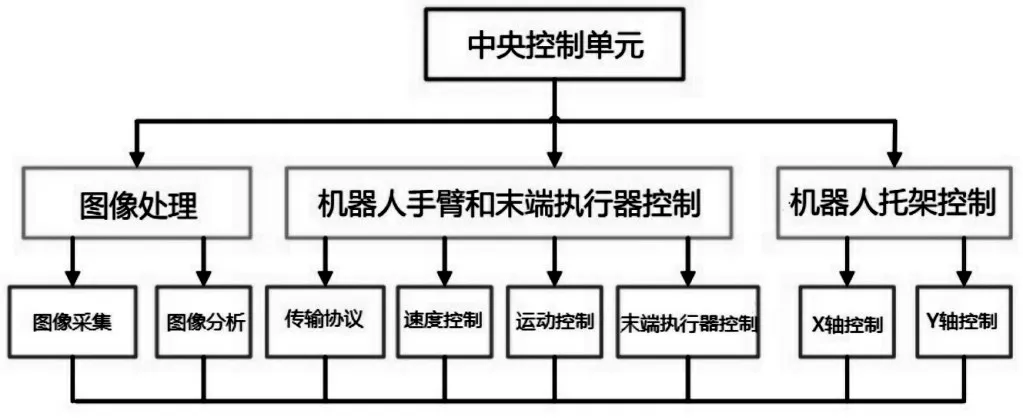
图2 并联机器人系统程序架构Fig.2 Parallel Robot System Program Architecture

机器人载体控制指令读写采用LabVIEW VISA（虚拟仪器软件架构）模块进行串口通信，首先读取操作员的命令，判断机器人载体是向前移动还是垂直移动。如果向前移动，机器人载体执行向前动作，判断是否到达设定位置。如果没有，它将继续前进如果向前动作已经到达位置，则该动作流程就完成了。如果垂直移动，判断运行系统是上升还是下降。这个动作流程将在它到达位置时结束。

3 机械臂运动学分析

六轴并联机器人正解解决的是从机器人关节到机器人末端姿态的传递关系，反解解决的是从机器人末端姿态到机器人关节角的传递关系。正反解是解决机器人在空间运动的关节角和空间位姿的传递关系。求解运动学逆问题的两种主要方法是解析法和数值法。

在第一类中，根据给定的位形数据对关节变量进行解析求解。在第二类解中，基于数值技术得到了关节变量。在数学上，虽然六轴并联机器人的运动学反解有一个封闭的数学解，但是运动学正解缺少一个封闭的解[9-10]。一般来说，方程的数量小于未知数的数量因此运动学正解表示一个待定问题。此外，运动学公式的高度非线性也增加了计算的复杂性。

3.1 机械臂运动学反解

通过逆运动学求解可以根据目标位置来控制机器人各个关节角度的相对运动。使用末端执行器的位置和方向满足待抓取目标位置和姿态。

3.1.1 坐标系建模

六轴并联机器人模型，如图3所示。

图3 六轴六轴并联机器人正面模型图Fig.3 Mechanism Diagram of Parallel Robot

图中：0-X0Y0Z0—基坐标系，位于基座上平面中心；P1-X1Y1Z1—中间坐标系，沿基坐标系Z0轴负方向平移H1距离；Pe-XeYeZe—末端坐标系；P2-X2Y2Z2—中间坐标系，沿末端坐标系Ze轴正向平移H2距离。小臂长度为LA，大臂长度为LB，六个电机驱动角分别为θi。假设1号电机驱动点位于A1点，Rb—中间坐标系P1-X1Y1Z1原点到A1的距离；αb1—X1轴与P1A1间夹角；γ1—X1轴与电机轴线夹角；Rm—末端坐标系Pe-XeYeZe原点到D1点在的距离；αm1—Xm轴与PeD1间夹角。

3.1.2 运动学反解

以第一连杆为例，B1点坐标为（B1x，B1y，B1z），可以写成如下形式：

把下角标“1”改为“i”即为六个连杆通用的方程，组成方程组即可求出正反解。

3.2 机械臂运动学正解

目前六轴并联机器人正解析解决办法有分析方法、迭代方法、使用额外的传感器和机器学习的方法等[11-13]。在并联机械手末端安装额外的传感器，以获得更多关于系统（机械手）状态的信息，有助于快速方便地求解运动学正解，但是传感器的额外成本让这种方法的应用受到限制。本节介绍的六轴并联机器人构型的神经网络和牛顿修正优化求解运动学正解方案。比较两个算法的优劣性，发现这里的方法具有减少计算资源使用、实时快速执行的优点。基于神经网络求解运动学正解的分析方法不仅限于六轴并联机器人的特殊结构，也可以推广到其他类型的六轴并联机器人。神经元处理单元对修改后的信号进行求和，并将该值应用于线性或非线性激活函数，其产生的信号或值被传送到输出单元，输入、权重、体系结构和阈值都是神经网络器可以控制的参数。

根据上面所述的非线性方程组，采用三层BP神经网络方法对六轴并联机器人运动学进行正向求解。根据六轴并联机器人的外观结构，建立基于神经网络的六轴并联机器人非线性方程。神经网络拓扑结构，如图4 所示。包括输入层，隐层和输出层。可经由下式将机器人正运动学的非线性映射转换为线性映射，设N个样本为(Pj，αj)，其中j=1，2，···，N。Pj为网络输入向量，作为第j个位置样本，αj作为第j个电机转角为网络输出向量。

图4 三层前向神经网络结构Fig.4 Three-Layer Feedforward Neural Network Structure

将六轴并联机器人运动控制过程中产生的位置和关节角度进行保存，作为大量样本输入测试后，可以获得机器人关节角度到机器人末端位置的运动学正描述，即可根据建立的非线性方程和权重得到六轴并联机器人正解。

3.3 牛顿修正（优化）法

在迭代方法中，运动学问题被公式化，因此可以使用任何可用的数值技术来求解。这些数值技术是计算密集型的，可以实时的进行正运动学的求解。牛顿修正法即把m步简化牛顿法合并，并作为基本牛顿法的一步来进行计算，文中取m=2。

式中：X—位置和姿态值。

其余矩阵元素将上面6个等式中的αm1、αb1、γ1、θ1、LA1替换为αmi、αbi、γi、θi、LAi即可得出。

计算过程不断循环下去，直到||ΔXk||＜ε或||F(Xk)||＜δ或计算周期大于N时（其中ε、δ为误差容限，N为最大迭代次数）输出Xk值。

在并联机器人运动学方程耦合、存在多解和奇异性的情况下，求解正运动学问题存在一定的困难。运动学正问题的数学解可能并不总是与物理解相对应，其求解方法取决于机器人的结构。从算法的实时性和计算效率来说，牛顿修正优化法是一个不错的选择。

4 视觉抓取

该系统可直接在真实的机器人平台上解决涉及不确定性的联合到达和抓取任务。即使具有最少的先验知识，系统也可以在短时间内学习且可靠地执行其任务。此外，该系统也描述了控制系统对变化和错误做出反应的能力。

4.1 视觉系统

以LabVIEW为开发环境，通过LabVIEW的图像处理工具包IMAQ（image AcQuisition）模块的图像采集卡对摄像头进行控制。在LabVIEW上开发了Vision Assistant 7.1的图像处理程序，并进行了集成应用。首先，相机获得良好的曝光图像并进行白平衡调整，从而获得良好的图像。该程序利用HSV的六棱锥模型，在图像处理算法中，通过HSV颜色规范的二值化来识别特征，对待抓取目标进行分级，然后在二维坐标上分别搜索待抓取目标的位置和外部特征。则从RGB到HSV的转换及实现公式如下：

视觉处理系统流程，该流程中最重要的是识别目标物体的特征，然后定位其中心位置以方便进行抓取，如图5所示。

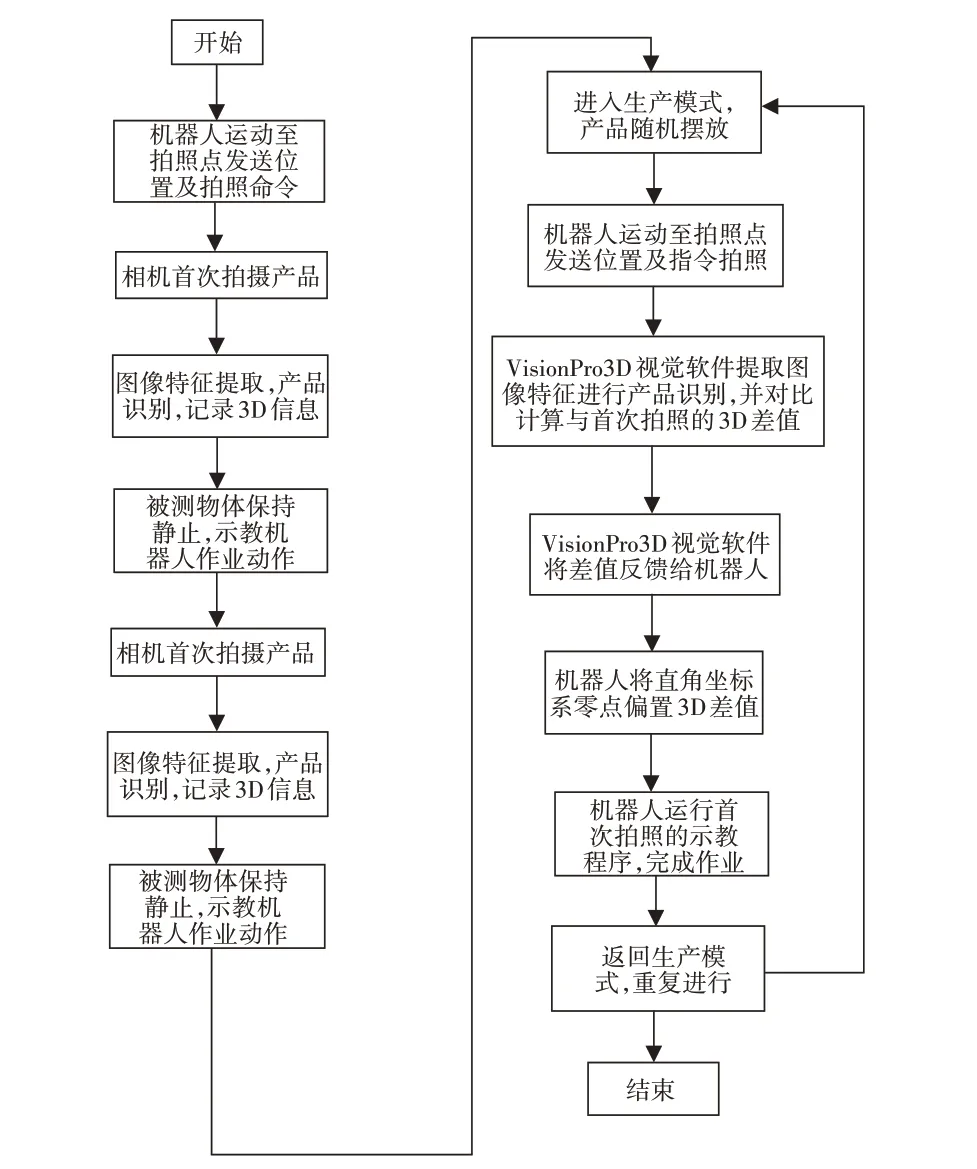
图5 视觉处理系统流程Fig.5 Visual Processing System Flow

4.2 视觉标定

为了获得高质量的目标物体的图像信息，正确地放置和安装摄像机是非常关键的。如图6所示，在该区域中所有棋盘的所有边角都应清晰可见，图像处理软件可直接检测棋盘的所有角点。该区域由（9×7）正方形的图案组成，由于外角不太可靠，可以有效地使用内部（7×5）的正方形，且图案的尺寸为（14×10）cm2，用高质量打印机打印，然后放在玻璃上。

图6 棋盘格Fig.6 The Checkerboard

在角点检测之后，根据张正友标定方法，工具箱用于执行摄像机校准，并基于棋盘角点检测提取相机的内外固参数，照相机捕获了不同位置和方向的几张棋盘图像，然后通过此工具箱将其加载到计算机中。通过四次鼠标单击手动定位每个棋盘方块的极角，然后工具箱使用其角检测算法找到角的位置。此时基于方程式（12）可以选择其他选项来改善校准结果，例如更改径向失真系数的值。

校准模型时，假设制造商提供了相机的某些参数，以减少估计的初步猜测。每个图像需要n个特征点（n＞8），并基于径向对齐约束通过一组n个线性方程组解决了校准问题。在不考虑偏心变形项的情况下，使用了二阶径向变形模型。两步法可以处理3D或平面校准网格的单个图像或多个图像。摄像机标定涉及的其坐标转换关系，如图7所示。

图7 坐标转换关系图Fig.7 Coordinate Transformation Diagram

式中：u—理想成像平面坐标；

d—实际的成像坐标系；

（O，u，v）—计算机图像坐标；

（cx，cy）—基准点；

f—摄像机的焦距；

k—径向畸变系数；

p—切向畸变系数；

相机标定校准一直是相机参数测量的必要组成部分。

4.3 图像处理

六轴并联机器人待抓取的目标是圆形彩色片，提取圆形样本，在直角坐标系中的图像空间中的圆对应着参数空间坐标系中的一个点，而直角坐标系中的图像空间中的一个点对应着参数空间中一个三维直立圆锥，因此在确定直角坐标系中的圆形，就可以在参数空间中求取各个圆相交的交点，该点约束了通过该点一族圆的参数（a，b，r）。

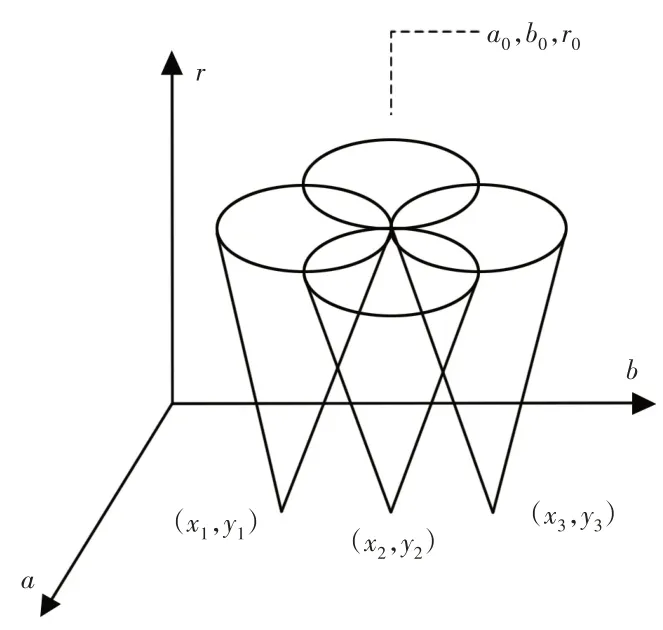
图8 点-线的对偶性Fig.8 The Duality of Point-Line

广义Hough变换将输入图像中圆边界上的点映射到三维的参数空间的锥面上去，最后这些圆锥就会相交于参数空间上某一点（a0，b0，r0），即可利用Hough变换检测圆形。最后用一阶矩M10和M01分别除以零阶矩M00得到的是物体的质心坐标。

5 实验

5.1 运动控制实验

机器人运动学是对机器人机械手运动的分析研究。机器人运动学建模主要有两种不同的空间，即笛卡尔空间和四元数空间。两个笛卡尔坐标系之间的变换可以分解为旋转和平移。

各个轴轨迹曲线，如图9所示。对机器人运动进行输入轨迹与输出轨迹进行验证，规划曲线和实际曲线一致。

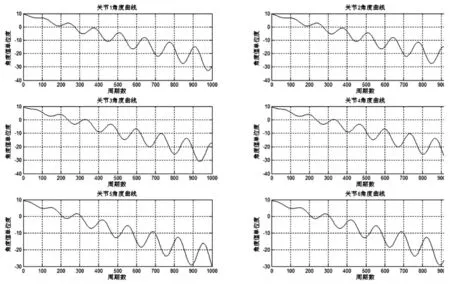
图9 各个轴轨迹曲线Fig.9 Trajectory Curve of Each Axis

5.2 视觉抓取实验

为了实际验证六轴并联机器人运动控制正确性，六轴并联机器人运动抓取示意图，如图10所示。六轴并联机器人为生产线系统提供了稳定运动控制功能，六轴并联机器人准确识别并同步跟踪传输线上高速运动的产品，在高速运动中连续抓取待抓取目标，然后整齐的摆放到指定目标。六轴并联机器人准确识别并同步跟踪传输线上高速运动的产品，在高速运动中连续抓取多包产品，然后整齐的摆放到包装箱中。

图10 运动抓取示意图Fig.10 Motion Grab Diagram

依靠千分表可以进行测试，得出六轴并联机器人重复定位精度为±0.05mm，运动速度快，拾放节拍为120次/分钟，其位置和方向参数的精度分别接近0.008mm和0.0012°。

6 结论

这里针对带有六个自由度的并联平台的机械结构的运动控制算法进行了深入的研究。六轴并联机器人致动器通过万向节连接到基座，并通过球形接头连接到上平台。六轴并联机器人运动学正解的求解是闭环控制系统的关键，缺乏一种封闭形式的数学解。鉴于此，在本文的模型中，将运动学关系方程作为切入点，提出了牛顿修正优化法正运动学控制方法，根据图像学形态特征开发了从图像信息中确定待抓取目标的图形特征，然后对其进行分拣抓取的功能模块。最后，这里对六轴并联机器人运动学和视觉抓取算法进行了验证，其位置和方向参数的精度分别接近0.008 mm 和0.0012°。结果表明该方法运动速度快，拾放节拍110次/分钟，验证了算法的有效性和正确性。