四驱电动轮汽车模糊逻辑控制的再生制动系统

刘晋霞，王 莉，刘宗锋

（山东科技大学交通学院，山东 青岛 266590）

1 引言

电动轮汽车相对传统电动汽车去掉了复杂的传动系统，具有结构简单，布置灵活等优点，进而成为电动汽车领域的重要发展方向。随着再生制动系统有效增加混合动力汽车的续驶里程的应用，其在电动轮汽车上的应用也成为了研究热点。

目前，关于电动轮汽车再生制动系统的研究主要侧重于控制策略及其与防抱死系统（Anti-lock Braking System，ABS）协同控制方面。文献[1]在重新设计电动轮汽车制动系统的基础上，采用以制动强度、电池荷电状态（State Of Charge，SOC）作为输入，电机制动力与总制动力之比作为输出的模糊控制器，对再生制动系统进行调控；文献[2]在对整车制动力分析的基础上，对比分析了并行制动力、理想制动力及最佳制动力控制策略对电动轮汽车再生制动系统的影响，在考虑制动强度的同时，对理想制动力控制策略进行了改进；文献[3]提出了一种理想制动力分配曲线，并计算轮毂电机在发电状态时输出特性的再生制动控制策略；文献[4]考虑了在紧急制动工况下再生制动系统的工作状态，并将ABS与再生制动系统协同控制使再生制动系统在紧急制动的工况下也参与制动。以上对于再生制动系统控制策略及其与ABS协同控制的仿真结果均表明，可有效的回收制动能量，提高电动轮汽车的续驶里程。

以上针对制动强度、电池SOC与轮毂电机输出特性中的一个或两个因素对电动轮汽车再生制动系统控制策略进行了研究。因此，综合分析制动强度、电池SOC与轮毂电机输出特性对电动轮汽车再生制动系统性能的影响，在根据制动强度对前、后轮同时抱死时，其制动力关系的理想制动力曲线、明确要求前、后轮制动力的ECE法规线进行计算的基础上，提出一种模糊逻辑控制的再生制动控制策略，将该控制策略用MATLAB/Simulink 进行建模，并嵌入到ADVISOR建立的整车模型中。在CYC_UDDS工况下，展开对四驱电动轮汽车模糊逻辑控制的再生制动系统性能的研究。

2 电动轮汽车再生制动系统

2.1 系统组成

这里以四驱电动轮汽车为研究对象，其再生制动系统[5]主要由包含轮毂电机与制动器的电动轮、电机与制动控制单元、电池、制动踏板及制动踏板、轮速与电池电流传感器等组成，如图1所示。制动踏板被踩下时，制动踏板传感器将检测到的制动踏板开度及位置等信号传送给整车控制器，整车控制器综合轮速与电池电流传感器等信息，计算整车总制动力FX，并为各电动轮确定电机制动力与制动器制动力的大小。电动轮汽车整车参数[6]，如表1所示。

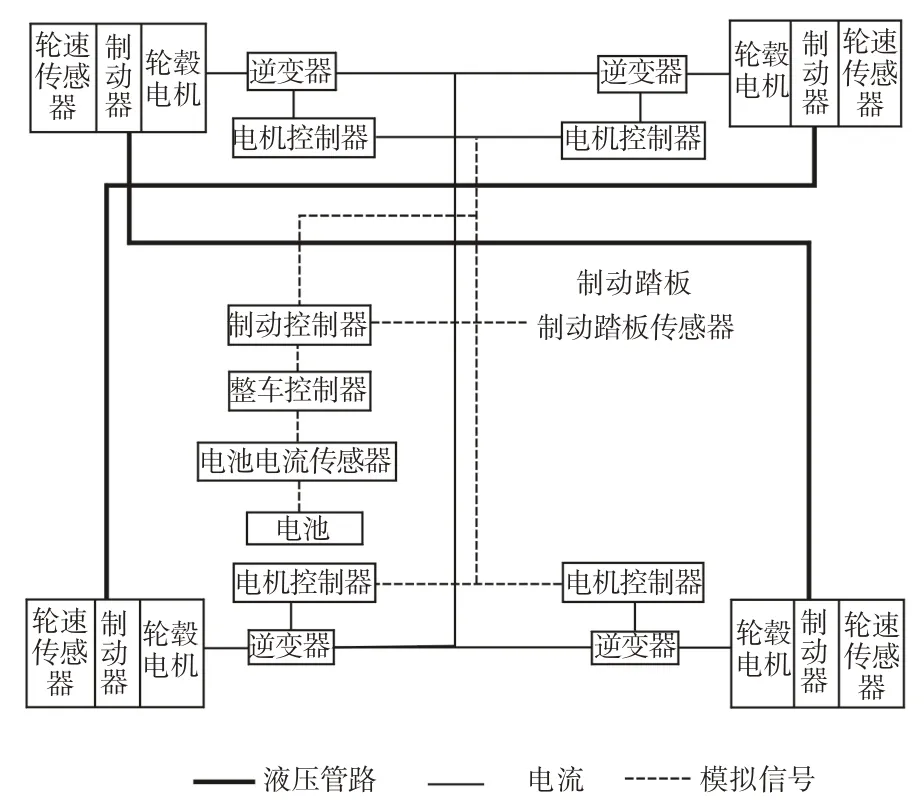
图1 电动轮汽车再生制动系统的组成Fig.1 Composition of Regenerative Braking System for Electric Wheel Vehicle

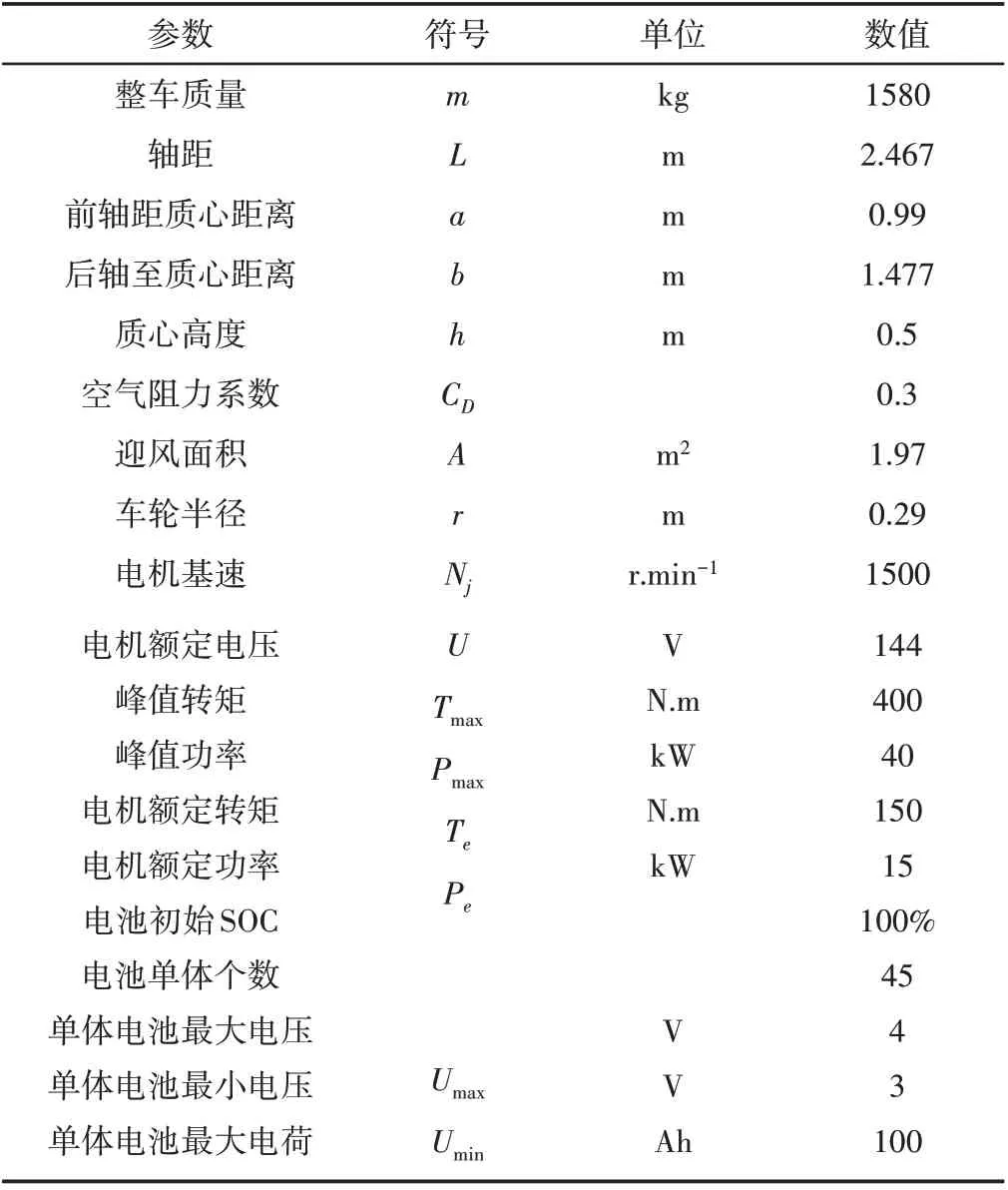
表1 电动轮整车参数Tab.1 Parameters of Electric Wheel Vehicle

2.2 工作原理

式中：r—车轮半径。

在制动过程中，电机制动力与制动器制动力之和的电动轮总制动力认为等于电动轮驱动力[8]。

当由电动轮汽车制动减速度与重力加速度比值决定的制动强度小于0.1时，所需整车总制动力较小，由电机制动力进行制动；当制动强度为（0.1～0.8）时，所需整车制动力较大，制动力优先由电机制动力提供，当电机制动力达到最大时，制动器则提供制动力且制动器制动力等于总制动力减去电机最大制动力；当制动强度大于0.8时，所需整车制动力骤然增大，为避免短时强电流充电影响电池使用寿命，只由制动器提供制动力。

当电池SOC 小于0.1、大于0.85时，为避免电池过放和电池过充而影响电池的使用寿命。

因此，这里设定当电池SOC小于0.1时，电动轮汽车停止工作；电池SOC大于0.85时，在任何制动工况下，再生制动系统不进行能量回收，从而不为电池充电。当电池SOC在（0.1～0.85）范围内且制动强度小于0.8时[1]，再生制动系统进行能量回收，同时为电池充电。

3 模糊控制器的设计

3.1 模糊控制策略制动力的分配

3.1.1 前、后轮制动力及电机与制动器制动力分配

理想制动力曲线可保证在制动过程中前、后轮同时抱死，即前、后轮制动力分别等于各自的附着力。

则前、后轮制动力满足[9]：

式中：m—整车质量；g—重力加速度；hg—质心高度；b—后轴至质心的距离；L—轴距；Fμ1—前轮制动力；Fμ2—后轮制动力。

为了保证电动轮汽车的制动稳定性及制动效率，ECE法规线有明确的要求：对于前、后轮制动力计算时，附着系数φ应满足：0.2＜φ≤0.8，且制动强度Z应满足：Z≥0.1+0.85（φ-0.2）。则前、后轮制动力应满足[10]：

在电动轮汽车电机制动力与制动器制动力分配时，优先采用电机制动。当整车总制动力较小时，完全由前轮电机制动力进行制动，则后轮制动力为零，通过式（4）可得前轮最大电机制动力Fmaxf为1608N。随着整车总制动力不断增大，当后轮电机制动力达到最大时，前轮制动力为其最大电机制动力与制动器制动力之和，通过式（2）～式（4）可得后轮最大电机制动力为1490N。

3.1.2 制动力分配曲线

由前、后轮最大电机制动力、理想制动力曲线及ECE法规线确定的制动力分配，如图2所示。图中：斜线—制动强度取值；A点—前轮最大电机制动力；B点—前轮电机制动力最大时与理想制动力曲线的交点，其制动力为FB；C点—制动强度为0.8的斜线与理想制动力曲线的交点，其制动力为FC。OA表示完全由前轮电机制动力进行制动；AB表示前轮电机制动力最大，剩余制动力由后轮电机提供；BC段表示前、后轮电机制动力与制动器制动力共同制动。

图2 制动力分配曲线图Fig.2 Brake Force Distribution Curve

当FX≤Fmaxf时，整车制动力由前轮电机制动力提供，按OA线进行分配。当Fmaxf＜FX≤FB时，整车制动力由前轮电机最大制动力提供外，FX-Fmaxf部分由后轮电机提供，按AB线进行分配。当FB＜FX≤FC时，整车制动力由前轮电机最大制动力提供外，FX-Fmaxf部分由后轮电机和前轮制动器制动力提供，直到后轮电机制动力达到最大；随着整车制动力的不断增大，便由前、后轮最大电机制动力与制动器制动力共同进行制动，按BC线进行分配。

当Z＞0.8时，完全由制动器制动力进行制动。

3.2 模糊控制策略结构的确定

采用应用广泛、响应快、无超调的Mamdani 型模糊推理模型。将整车总制动力与电机提供的最大制动力Fmax之差Fδ、电池SOC 和制动强度Z设为3 个输入变量，以及电机制动力与整车总制动力之比设为输出量K[11]。其模糊控制策略结构，如图3所示。

图3 模糊控制策略结构图Fig.3 Structure Diagram of Fuzzy Controller

3.3 输入、输出量的模糊子集与隶度函数的选取

制动时Fδ的论域为[-100，100]，将其所在论域的模糊子集分为5个，分别为{NB（负大），NS（负小），O（正好），PS（正小），PB（正大）}，其隶属度函数的选取，如图4所示。

图4 Fδ隶属度函数Fig.4 Membership Function for Fδ

电池SOC的论域为[0，1]，将其论域的模糊子集分为3个，分别为{L（小），M（中），B（大）}，其隶属度函数的选取，如图5所示。

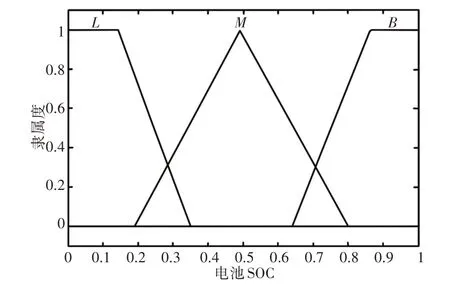
图5 电池SOC隶属度函数Fig.5 Membership Function for SOC of Battery

Z的论域为[0，1]，将其论域的模糊子集分为3个，分别为{L（小），M（中），B（大）}，其隶属度函数的选取，如图6所示。

图6 Z隶属度函数Fig.6 Membership Function for Z

输出量K的论域为[0，1]，将其论域的模糊子集分为3个，分别为{L（小），M（中），B（大）}。

3.4 模糊逻辑控制规则

由于Fδ中有5个模糊子集，电池SOC、Z分别有3个模糊子集，因此模糊逻辑控制规则共有45 条，采用的语言控制规则为“若......，则……”（if……，then……）句型。

根据制定的模糊控制规则，其输出变量K与输入变量Fδ、电池SOC关系，如图7所示。由图可知，当电池SOC（SOC＜0.65）为定值，且-50＜Fδ＜50时，K随Fδ的增大而减小；当Fδ（-50＜Fδ＜50）为定值，且电池SOC≥0.85时，K随电池SOC的增大而减小。

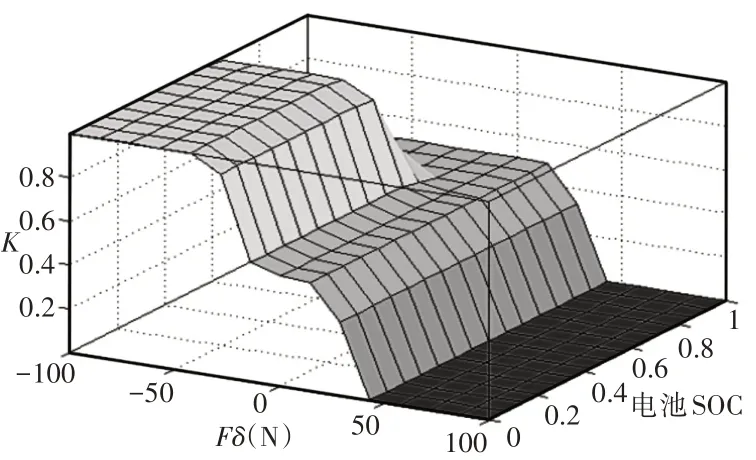
图7 输出量K随输入量Fδ、电池SOC变化的曲面Fig.7 The Surface of the Output Variable K Varies with the Input Variable Fδ and SOC of the Battery

输出变量K与输入变量Fδ、Z的关系，如图8所示。由图可知，当Z（Z＜0.65）为定值，且-50＜Fδ＜50时，K随Fδ的增大而减小；当Fδ（-50＜Fδ＜50）为定值，且Z＞0.8时，K随Z的增大而减小。

图8 输出量K随输入量Fδ、Z变化的曲面Fig.8 The Surface of the Output Variable K Varies with the Input Variable Fδ and Z

3.5 输出模糊量的清晰化

在模糊推理过程中，由于两个或多个输入量输出的隶属度函数逻辑的并集为分段、不规则形状，因此其输出是模糊量。输出模糊量清晰化的过程是将一个输出的模糊量转化成为一个确定的量，此处利用加权平均法去模糊化[12]。

4 仿真分析及结果比较

基于以上对模糊逻辑控制策略制动力的分配，结构图的确定及模糊规则的制定，这里在Matlab/Simulink中搭建其制动力分配模型，如图9所示。

图9 基于模糊控制的制动力分配模型Fig.9 The Braking Force Distribution Model Based on Fuzzy control

对ADVISOR进行二次开发，搭建电动轮汽车整车模型。将模糊逻辑控制的制动力分配模型嵌入到电动轮汽车整车模型中，选取美国公路循环工况（CYC_UDDS）[13]，将循环次数设置为5次进行仿真。将该模糊逻辑控制策略与ADVISOR自带查表法控制策略进行仿真对比，其电池SOC及实际车速与理论车速之差，如图10、图11所示。由图10可知，在模糊逻辑控制策略与查表法控制策略下，当电池SOC下降到0.1 时可行驶的时间分别为5205s和4570s，模糊逻辑控制策略使电动轮汽车行驶时间增加12.2%。

图10 两种控制策略的电池SOCFig.10 The Battery SOC for Two Control Strategies

图11 两种控制策略车速与理论车速之差Fig.11 The Difference Between Two Control Strategies and Theoretical Speed

由图11 可知，在模糊逻辑控制策略与查表法控制策略下，实际车速与理论车速出现车速差的时间分别为4308s和4270s。且模糊逻辑控制策略的车速差明显小于查表法控制策略的车速差。

5 结论

针对四驱电动轮汽车，在综合考虑制动强度、电池SOC及轮毂电机输出特性的基础上，提出一种再生制动系统的模糊逻辑控制策略，并与ADVISOR查表法控制策略进行对比分析得出，该控制策略下，电动轮汽车行驶时间增加12.2%，滞后38s出现车速度差，且车速差明显减小。因此，该模糊逻辑控制策略能够使电动轮汽车有效的回收制动能量，增加续驶里程，且具有良好的稳定性。