CAE优化驱动的某型号起落架结构设计方法研究
赵飞虎,罗卫东,2,钱庚建,樊战军
(1.贵州大学机械工程学院,贵州 贵阳 550025;2.贵州大学明德学院,贵州 贵阳 550025;3.贵州航天天马机电科技有限公司,贵州遵义 563000)
1 引言
结构设计是机械产品设计的主要部分[1]。而进行结构设计时,最主要考虑的要是性能、成本和研制周期。目前普遍的设计思路,如图1所示。依照设计要求、工艺可行性、结构可装配性再结合设计人员的工程经验来设计产品概念模型;然后进行性能验证,将不满足设计要求的结构返回CAD设计环节人工修改,重新验证,如此反复人工迭代。该设计方法对设计人员的工程经验有较高要求,且效率低、设计周期长,工程经验不足的设计人员很难掌握该设计方法,无法设计出最合理的结构。

图1 原起落架结构设计流程Fig.1 Design Process of Original Landing Gear Structure
随着CAE优化技术不断的发展和完善,设计人员将其引用到设计流程中来,如2018年,文献[2]以某型舰炮托架为对象进行拓扑优化设计,使托架质量减轻了16%,实现轻量化;2015 年,文献[3]以某机翼身对接加强框作为研究对象进行了拓扑优化和尺寸优化两级优化设计,使质量和性能都获得了一定程度的提高。
虽然CAE 优化技术在设计流程中的运用比例在逐渐的增加,取代人工的一部分工作。但使用较为单一,主要针设计过程中的校核以及成型产品后期的优化。不能从根本上解决现行方法中大部分工作依赖人工经验进行迭代设计,造成设计周期长、结果不合理的问题。针对目前结构设计中存在的不足,提出了一种CAE优化驱动的结构设计方法,根据不同设计阶段的需要,运用相应的技术支撑,形成一个完整的CAE优化驱动设计的流程,使CAE优化技术贯穿设计。最后,以某发射车起落架为研究对象,详细分析了其使用要求,采用新的设计方法对其进行了优化设计,验证了新方法的可行性。
2 结构设计策略
结构设计首先是构型设计,其本质是结构传力路径的选择,即根据产品的受力分析确定结构承载特点,寻求设计区域中最佳的传力路径。拓扑优化技术在寻找结构最佳承力路径的应用上使用的最广泛,其内容是在一个确定的连续区域内剔除不满足约束条件的材料获得最佳的承力路径,得到结构在设计区域内材料分布[4-5]。
尺寸优化技术是一种常用的局部优化方法[6],是在结构总体形状确定后设计人员用来进行详细设计和局部尺寸调节的工具。主要通过改变结构的几何尺寸(厚度、长度、宽度)以及两构件的相对位置,来达到提升结构性能的要求。尺寸优化涉及到参数化建模,即使用变量来驱动模型结构的调整。这样可以摈弃一般设计方法中采用人工进行模型修改的步骤,方便软件在优化过程中自动寻找给定约束条件下的最优解。在进行优化时,某些结构中具有多个变量,但部分变量对优化的目标影响较小甚至没有影响,若采用全部变量进行优化设计,则会耗费较多不必要的优化时间,需对参数进行灵敏度分析,挑选对优化结果影响较大的变量进行目标优化。
借助CAE优化技术在结构设计上具有快速便捷的优势,综合运用结构设计方法,提出一种CAE优化驱动的桁架式结构设计流程,首先,在结构可行设计空间运用拓扑优化寻找给定载荷与边界约束下的结构主要承力路径,对选出的承力路径利用桁架结构进行模型重构,仿真验证模型的力学性能,在此过程中反复的调整模型,直至获得满足使用性能最低要求的模型,完成结构的概念建模;其次,参数化概念模型,对所有参数进行灵敏度分析,确定对优化目标影响较大的参数,运用尺寸优化技术,进行单/多目标的结构性能优化,形成结构的基本构型方案;最后,基于尺寸优化的结果,考虑生产水平、装配条件、结构平顺性等确定参数最终尺寸,形成结构的详细设计方案。完整的流程,如图2所示。在静力学的运用中,结构优化建模主要分为两种:(1)在体积或质量约束下寻求结构刚度最大化(最小柔度);(2)在刚度约束条件下寻求结构最小体积或最小质量。
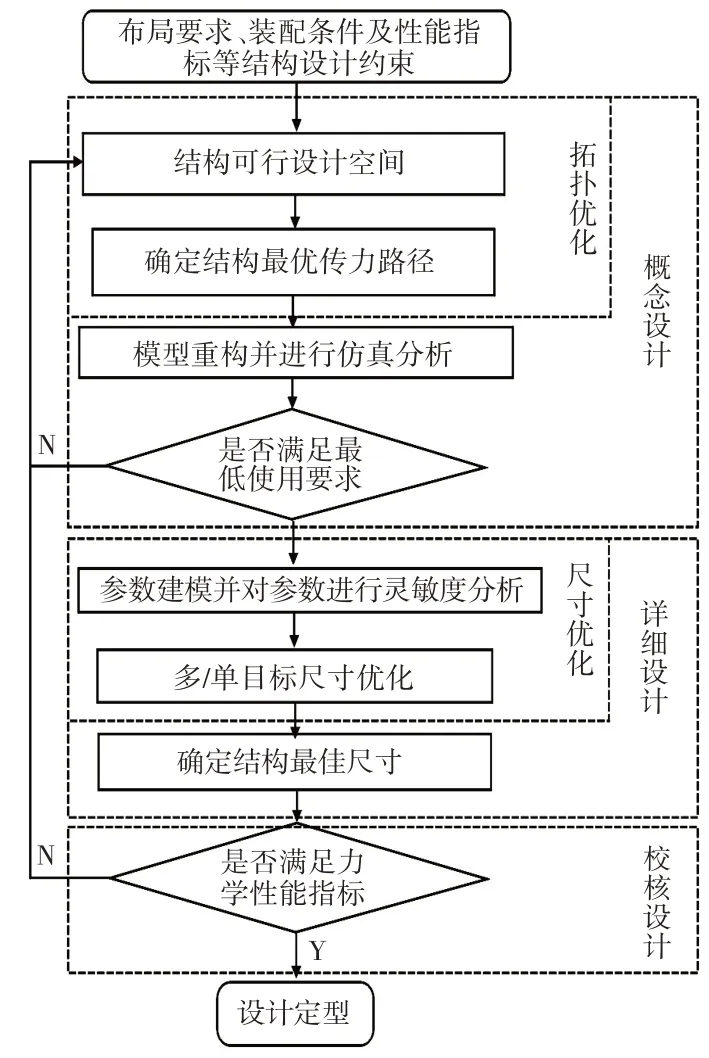
图2 新起落架结构设计流程Fig.2 New Landing Gear Structure Design Process
流程中拓扑优化属于第一种结构优化问题。数学模型可描述为:(1)起落架可行设计空间内的单元相对密度为设计变量;(2)设定结构体积分数作为约束条件;(3)目标为结构刚度最大化。理论数学模型可表示为:

式中:x—设计变量;xi—单元设计变量;C(x)—结构柔度;N—单元数量;P—惩罚因子;ui—单位矩阵;ki—单元刚度矩阵;K—结构整体刚度矩阵;U—结构位移矩阵;F—结构所受载荷矢量;V—设计变量状态下的结构有效体积;V0—设计变量取1 状态下的结构有效体积;f—材料用量的百分比;Gk(x)-G*≤0—尺寸约束;xmin和xmax—x的上下限[7],引入xmin—防止单元刚度矩阵出现奇异[8]
流程中尺寸优化主要用于在满足结构重量的约束条件下实现所受最大应力值的最小化。数学模型为:在给定边界条件下,以桁架式支架结构中危险截面的厚度为设计变量,以设定的起落架质量为约束条件,实现结构所受最大应力值得最小化。数学模型可表示为:

式中:x—设计变量,取值范围为[xa,xb];σmax(x)—起落架结构所承受的最大应力值;M*-MS(x)≤0—质量约束。
3 某型号起落架结构设计
起落架是导弹发射车上的重要组成部件,主要用来固定弹并调整发射时的角度[10],是保证安全运输、快速发射的关键。设计起落架时主要考虑承载力、抗变形能力以及稳定特性,在达到性能要求的同时尽可能使其轻量化。
根据原结构进行设计要求分析,原起落架剖视图所示,起落架为一种左右对称的结构,如图3所示。弹筒为斜推式装卸,与起落架采用易装夹的块压紧式连接,导弹为倾斜式发射。故上部设有耳轴孔1 与起竖电缸进行连接;端面有四个接触面用于弹筒的固定;下部设有耳轴孔2,与副车架上的固定耳轴进行连接,可绕其旋转,不可以移动。结构材料使用20#钢,许用应力可表示为:
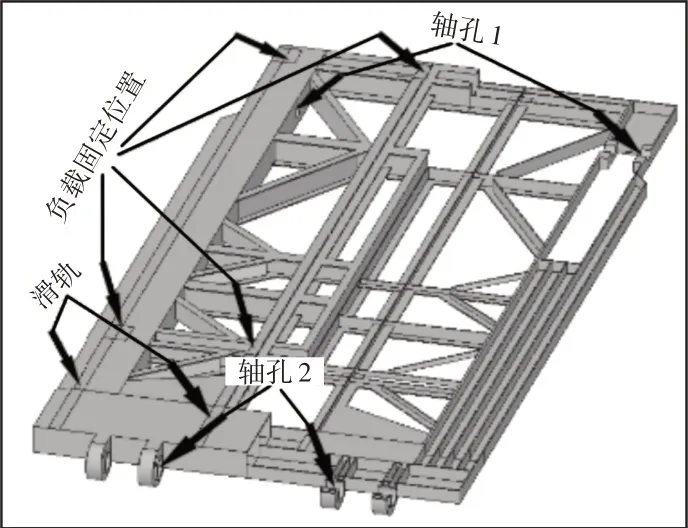
图3 原起落架结构剖视图Fig.3 Sectional View of the Original Landing Gear Structure

式中:στ—材料许用应力;σs—材料极限应力,其值为245MP;s—最小安全系数,一般取值范围为(1.5~3),新设计结构最小安全系数取值为2,故最大许用应力值为120MP。
3.1 概念构型设计
为得到最大限度的优化结构,保留必需的装配部位轴孔1和2、滑轨以及固定弹筒的4个接触面,其余皆设为设计区域。起落架为对称分布的桁架结构,为缩短拓扑优化的时间,将其简化为一个薄壁板进行分析。
选择最恶劣的临界起竖静力学工况来确定最优的传力路径。该过程的受力情况,如图4(a)所示,起落架受到弹筒质量产生的远端力A、电缸的起竖力C 和轴孔2对其约束力B的共同作用。
拓扑优化数学模型可抽象为:(1)设计变量为可行设计空间的单元虚拟密度;(2)约束条件为设计空间体积分数;(3)优化目标为静力工况条件下起落架柔度最小。
根据已建立的拓扑模型,应用Ansys软件中的Topology Optionization模块开展拓扑优化迭代。
如图4(a)所示,结构临界起竖静力学工况下的力加载情况,调整优化数学模型中保留的体积分数为70%、40%、30%、10%进行拓扑优化,得到优化后的结构,如图4(b)~图4(f)所示。
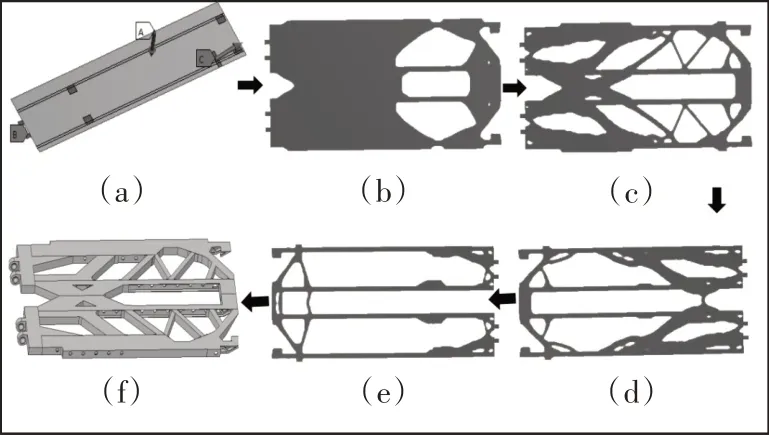
图4 起落架概念模型Fig.4 Conceptual Model of Landing Gear
观察可知,图4(e)材料过少难以满足结构力学性能要求,图4(b)保留材料过多,难以实现轻量化。综合考虑起落架实际工况多受力复杂,选择保留体积为40%的起落架概念模型图4(c)为传力路径。对图中材料分布部分用类似大小的平顺桁架结构代替,获得图4(f)重构后的起落架概念模型。
基于桁架结构设计策略,结合工程设计经验,将桁架概念模型所有截面的初始厚度设为6mm,对其进行静力学工况分析,如图5所示。可知起落架的整体应力低于85MP以下,可满足使用要求,但出现部分危险截面应力值较大的情况,最大为179MP,应对其进行优化处理。

图5 起落架概念模型应力云图Fig.5 Stress Cloud Diagram of Landing Gear Conceptual Model
3.2 详细模型设计
将概念模型中应力较大的地方进行增加板件或倒圆角处理,并设其厚度为优化变量,变量的初始值和设计区间如表1所示。表中:dv_1-dv_10—尺寸厚度;dr_11、dr_12—圆角半径。分别对应图中所表示的位置,如图6所示。

表1 尺寸优化设计变量的优化区间Tab.1 Optimization Interval of Dimension Optimization Design Variables
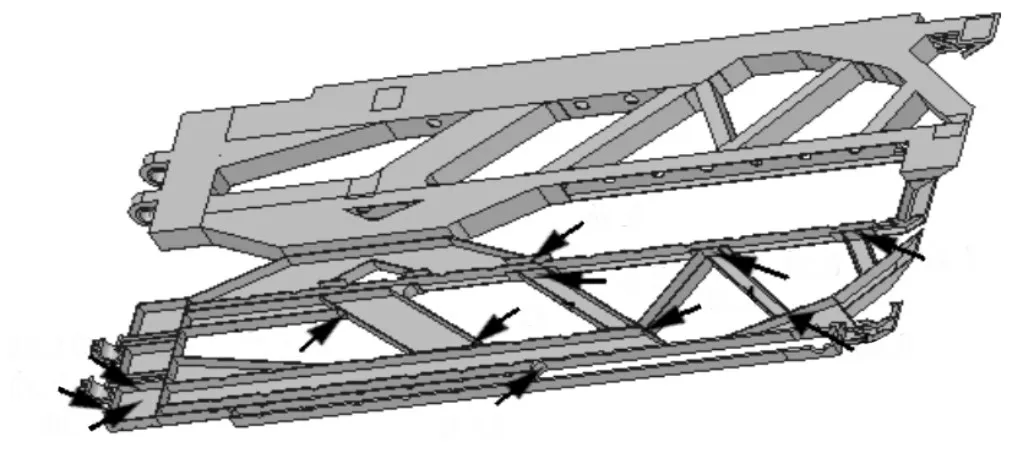
图6 尺寸优化设计变量示意图Fig.6 Schematic Diagram of Dimension Optimization Design Variables
以结构所受最大应力值为响应目标,应用workbench 软件中Response surface 模块分析变量对响应目标的灵敏度,如图7所示。

图7 设计变量灵敏度Fig.7 Sensitivity of Design Variables
分析可知dv_2、dv_4、dv_11对最大应力值有明显影响,其他变量影响较小,故选截面厚度dv_2、dv_4以及圆角半径dv_11作为尺寸优化的设计变量进行优化分析。
尺寸优化数学模型为:(1)设计变量为截面厚度dv_2、dv_4,圆角半径dv_11;(2)约束条件为起落架质量不超过993kg;(3)优化目标为起落架所受最大应力值最小。应用Ansys软件optimization模块展开尺寸优化迭代。优化过程中目标函数起落架所受最大应力值与约束限制起落架质量的迭代曲线,如图8、图9所示。
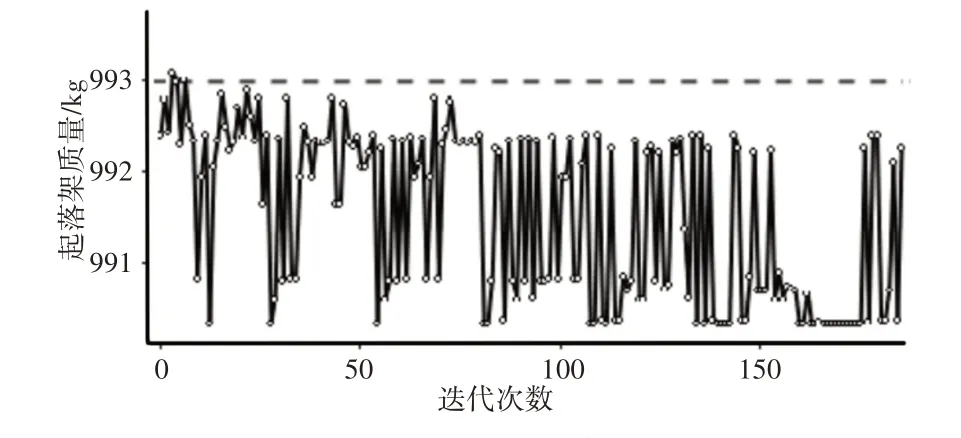
图8 起落架质量迭代曲线Fig.8 Iterative Curve of Landing Gear Mass
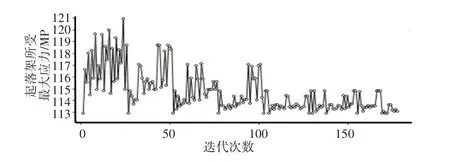
图9 起落架所受应力迭代曲线Fig.9 Iterative Stress Curve of Landing Gear
结构的最大应力值在(113~121)MP之间变化。随着迭代的进行,变化的幅值在逐渐的变小,经过180次迭代后,结构的最大应力值趋于113MP。而在迭代过程中,起落架的质量值小于993kg,随迭代的进行曲线呈不规则变化。该现象与设置的质量小于993kg下搜寻结构所受最大应力值最小化的目标一致。最终优化值,如表2 所示。优化后最大应力值由120MP 降低为113MP,质量由990kg升至993kg。
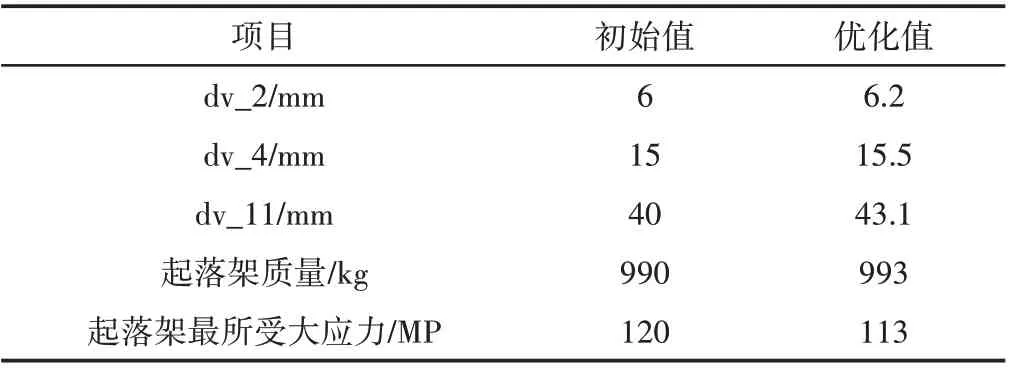
表2 尺寸优化设计变量与最优值Tab.2 Variables and Optimal Values of Size Optimization Design
由表2可知,危险截面处的尺寸对整个结构的最大应力值有较大的影响,通过改变危险截面出的尺寸能很大程度上降低结构所受的最大应力值,对整体的质量影响较小。
4 仿真校验
根据优化后的具体尺寸调整起落架模型,并对其进行仿真分析,验证结构在静态、模态和安全性方面的性能。为便于分析比较,原结构和新设计结构相对应的性能,如表3所示。原起落架静态应力云图,如图10所示。新设计起落架静态应力云图,如图11所示。
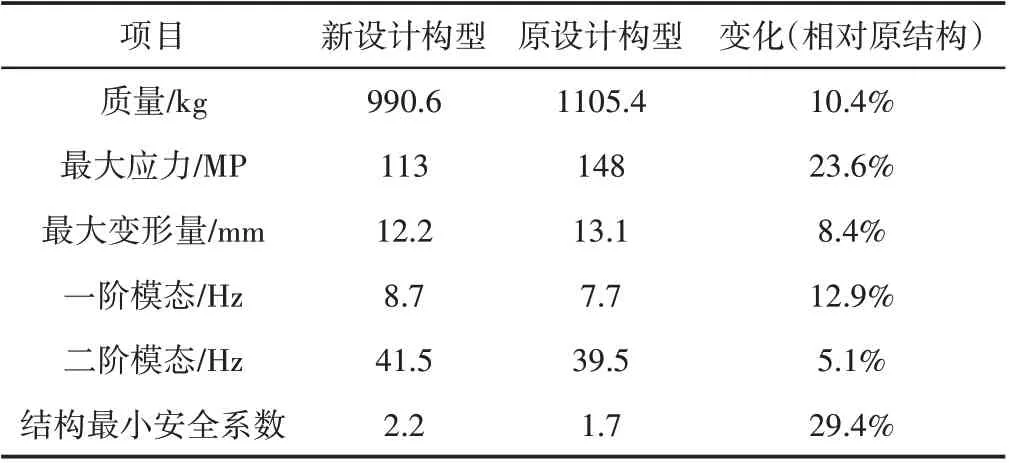
表3 两种结构质量与力学性能对比Tab.3 Comparison of Mass and Mechanical Properties of the Two Structures

图10 原起落架应力云图Fig.10 Stress Cloud Diagram of the Original Landing Gear

图11 新设计起落架应力云图Fig.11 Stress Cloud Diagram of the Newly Designed Landing Gear
5 结论
(1)提出一种CAE优化驱动的某型号起落架结构设计方法。在设计流程中先后应用拓扑优化、尺寸优化等技术,将CAE优化技术融合到设计的流程中来。实现了结构从概念构型设计到详细模型设计,形成一个完整的起落架结构设计流程。
(2)完成了设计后结构的力学性能验证,并与原设计结构进行对比分析。结果表明,相对于原设计结构,新型起落架结构质量减少10.4%,所受最大应力降低23.6%,最大变形下降8.4%,同时结构在稳定性、安全性等方面均有一定程度的提升,达到起落架的使用要求,验证了该设计方法在工程应用上具有可行性。
(3)新设计方法结合CAE技术和结构设计理论,采用软件迭代代替人工迭代,具有操作简单、设计速度快、对设计人员依赖少等优点。CAE优化驱动结构设计的方法能切实提高设计效率和性能,为同类结构设计提供一种新的设计思路。

