地铁换乘站基坑变形流固耦合数值分析研究

朱恒华，卫如春，贾超，唐俊平，李双

(1.山东省地质调查院，山东 济南 250014；2.山东大学海洋研究院，山东 青岛 266237；3.山东大学海洋地质与工程研究所，山东 青岛 266237；4.山东轨道交通工程咨询有限公司，山东 济南 250101)

0 引言

随着城市规模的扩大和城市人口的增加，人们出行需求急剧增长，而地铁因其具有运量大、有效利用地下空间等优势，现已作为大型城市的重要公共交通工具[1-2]。建设地下轨道交通体系是缓解城市交通压力的重要途径，不同地铁线路之间的交叉节点一般会设计成换乘车站，地铁换乘车站与一般车站形式的不同使得换乘车站基坑工程具有一定的特殊性[3]，而且换乘站往往处于城市人口集中，建筑密集的区域，在施工过程中要严格控制其变形及对周边环境产生的影响[4-5]，进行基坑开挖变形分析研究，掌握其变形规律尤显重要。

目前有限元单元法在基坑变形分析中被广泛采用，特别是三维有限元模型能够更好的反应基坑空间效应，模拟结果更加接近实际[6-7]。目前地铁换乘站基坑开挖数值模拟中较少考虑地下水渗流的应力耦合作用[8-9]，对于有降水的基坑工程，地下水渗流的影响更是不可忽视[10-12]，即使考虑渗流影响的基坑开挖，其数值模拟更多采用二维有限元模型[13-14]。针对这一问题，考虑济南水文地质特性[15]，本文针对济南长途汽车站地铁换乘站建立了考虑流固耦合的三维有限元模型，得到了基坑地连墙变形和周围地面沉降模拟结果，并对地铁换乘站基坑变形规律进行了总结和分析，可为类似地铁换乘站基坑变形的数值模拟和设计提供参考和借鉴。

1 工程概况

本文以济南长途汽车站地铁站基坑工程为研究背景，该工程位于济南市济泺路与北园大街交叉口，为R2线与M2线的L型换乘车站的节点工程，其中R2线东西向布置，M2线SN向布置，基坑平面布置图见图1。该站在R2线为地下两层岛式站台车站，开挖深度16.7～18.2m，M3线为地下三层岛式车站，开挖深度25.9m。基坑围护结构采用地下连续墙，地下连续墙厚度为800mm，在地下二层与地下三层相交位置，设置1排桩径为1000mm的钻孔灌注桩，坑内有五道钢筋混凝土支撑，尺寸为1000mm×1000mm(宽×高)。

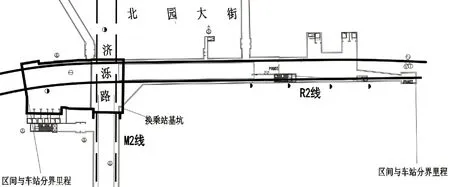
图1 基坑平面布置示意图

地下两层车站(非换乘区)开挖时，基坑竖向分4层开挖，其中开挖第2层时，分2步开挖，每步开挖3.75m，地下3层车站(换乘区)竖向分7层开挖，前4层开挖工序同地下2层，初始地下水水位位于地表面，每步开挖前先降水至开挖层层底以下，支撑布置原则为开挖至每道支撑设计标高以下0.5m位置时，布置支撑，之后再开挖下1层，开挖分层及地层剖面见图2。

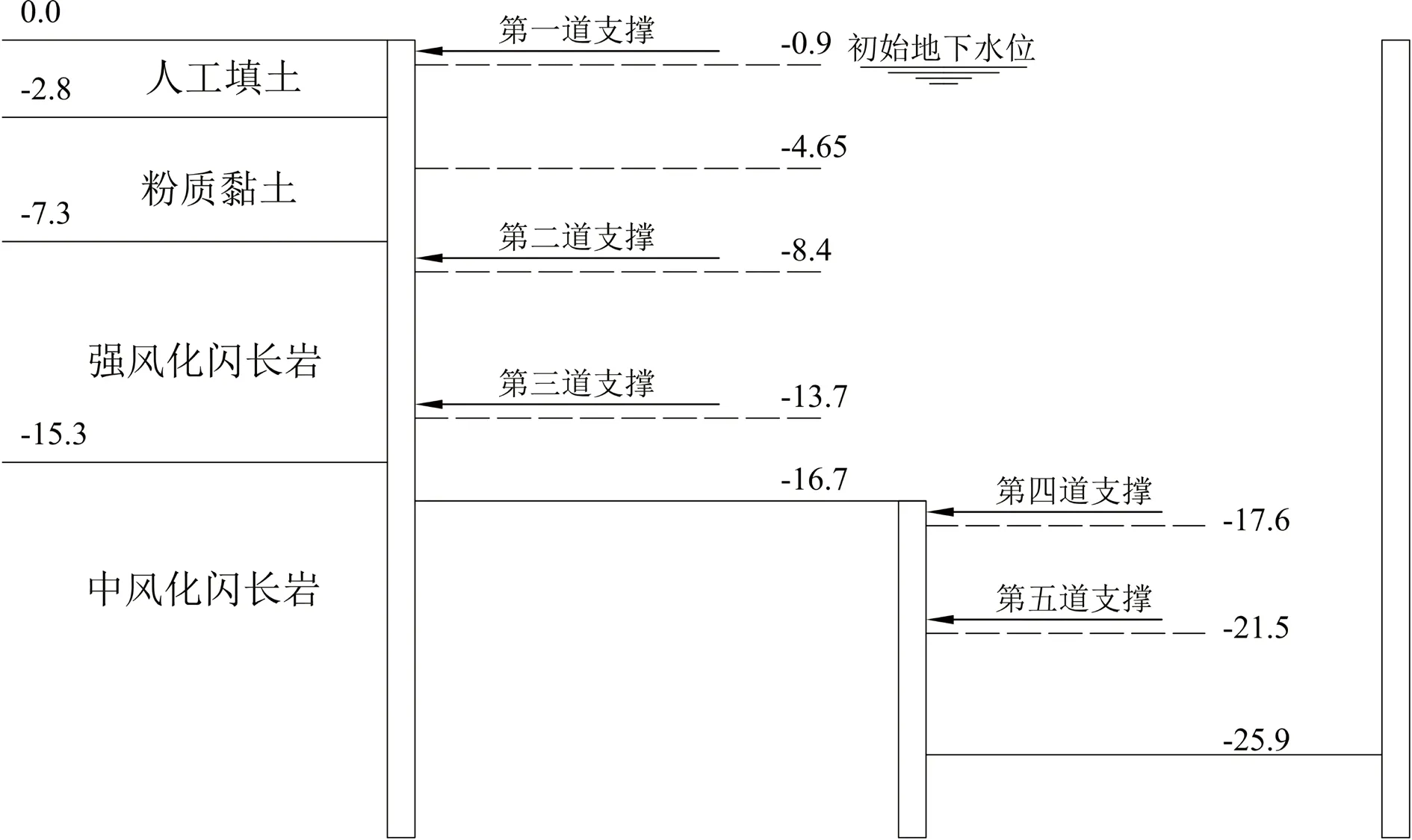
图2 基坑分层开挖剖面示意图(单位：m)

2 理论基础

2.1 本构模型

岩土体模拟使用的本构模型为Mohr-Coulomb模型，其表达式(式1)：

τ=c+σtanφ

(式1)

式中：τ—剪应力(kPa)；c—黏聚力(kPa)；σ—正应力(kPa)；φ—内摩擦角(°)。

2.2 渗流-应力耦合计算理论

渗流-应力耦合计算使用比奥固结理论，三维比奥固结方程见(式2)：

(式2)

式中：G—剪切模量(kPa)；ν—泊松比；wx，wy，wz—3个方向上的位移分量(m)；u—孔隙水压力(kPa)；γ—土的重度(kN·m-3)；k—3个方向上的渗透系数(k/cm/s)；γw—水的重度(kN·m-3)。

2.3 混凝土构件力学模型

与一般基坑相比，地铁换乘站基坑可分为换乘区和非换乘区两部分，当换乘区和非换乘区公共部分的土层开挖完成后，会在换乘区继续向下开挖一定深度，因此除了外部支护，在坑内换乘区和非换乘区的分界面会增加额外的内部支护(图3)。

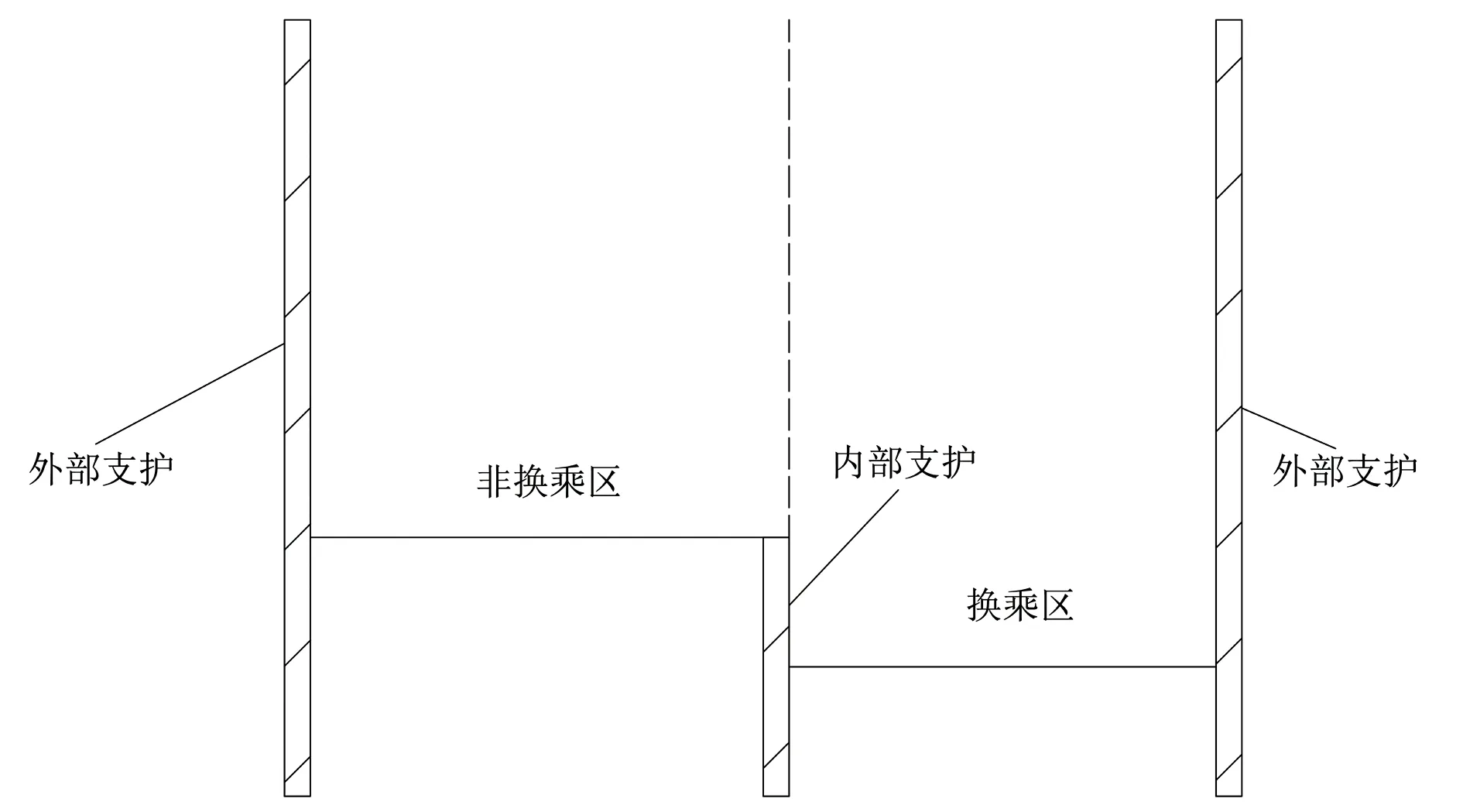
图3 换乘站基坑示意图

实际工程中，通常使用地下连续墙作为外部支护，而内部支护则使用钻孔灌注桩，在数值模拟中往往根据抗弯刚度等效原则将灌注桩折算成的连续墙进行模拟计算[9]，见(式3)：

E1I1=E2I2

(式3)

式中：E1和I1为灌注桩弹性模量(kPa)和惯性矩(m)；E2和I2为折算后连续墙的弹性模量(kPa)和惯性矩(m)，假设换算前后弹性模量相等，墙厚计算公式见(式4)：

(式4)

式中：D—桩径(m)，L—墙长(m)，H—墙厚(m)。

但是这种折算方法只考虑了灌注桩在垂直方向的连续性，没有考虑其在图4中x轴方向的不连续性，若计算得到H≠D，会改变灌注桩在图4中y轴方向的截面特性。因此，为了使折算结果更加合理，需要改变折算墙的弹性模量。

如图4所示，当D=H时，根据(式3)和(式4)，可得(式5)：

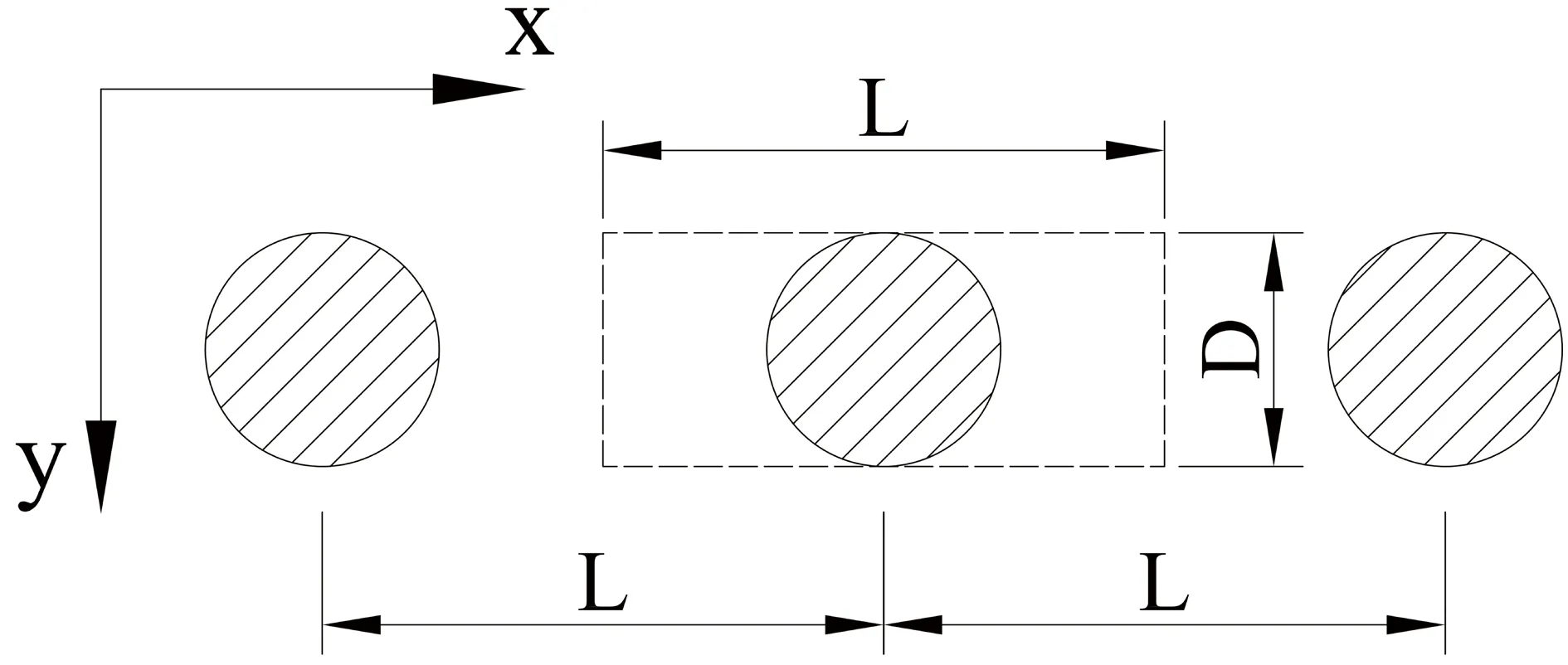
图4 等效抗弯刚度计算图

(式5)

3 数值分析计算

针对本文研究对象，采用Abaqus建立三维有限元模型进行分析计算[16]。

3.1 数值模型建立

3.1.1 模型范围

为探究一般规律，结合工程背景和模型的收敛要求，模型中基坑平面简化为长90m和宽50m的矩形，其中非换乘区长55m，最大开挖深度16.7m，换乘区长35m，最大开挖深度25.9m考虑对称性，取1/2建模(图5)。为了减小模型边界条件对基坑变形的影响，基坑边缘到土体模型外侧边界的距离应大于5倍的最大开挖深度，坑底到土体模型底部边界的距离大于2倍最大开挖深度，所以土体三维模型的尺寸为长350m×宽160m×深80m。

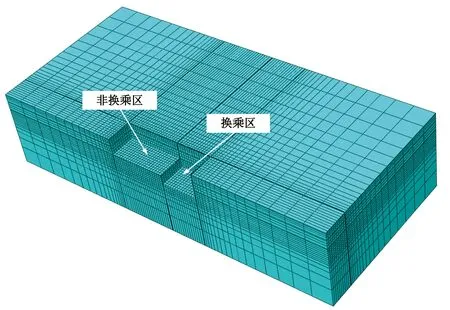
图5 土体三维模型图

3.1.2 网格及单元类型

岩土体单元类型为线性八节点六面体减缩积分渗流单元(C3D8RP)，单元数为61088，结点数为66528。

模型中基坑外围地连墙厚度0.8m，深度为28.9m，地连墙单元类型为C3D8R，单元数为34200，结点数为52338。

基坑内部支护结构为钻孔灌注桩，桩径1m，桩长12.9m，模型中根据(式5)将其折算为厚度1m，高度12.9m的连续墙体，折算墙将承受较大弯矩所以单元类型选择使用线性八节点六面体减缩积分非协调单元(C3D8I)，该单元能够更好的模拟与弯曲相关的变形，单元数为2500，结点数为3978。

本研究中支撑为次要结构，因此模型中所有支撑均选用梁单元，单元类型为B21。

3.1.3 模型参数

数值模拟采用弹性模型和Mohr-Coulomb模型2种本构模型，其中弹性模型用于墙体和支撑以及中风化闪长岩，Mohr-Coulomb模型用于其他岩土体，具体计算参数见表1(1)中国有色金属工业西安勘察设计研究院，济南市轨道交通R2线一期工程KC02标段长途汽车站详细勘察阶段岩土工程勘察报告(JNR2.KC02.C08-X-BG.ZS.01)，2016年。和表2。

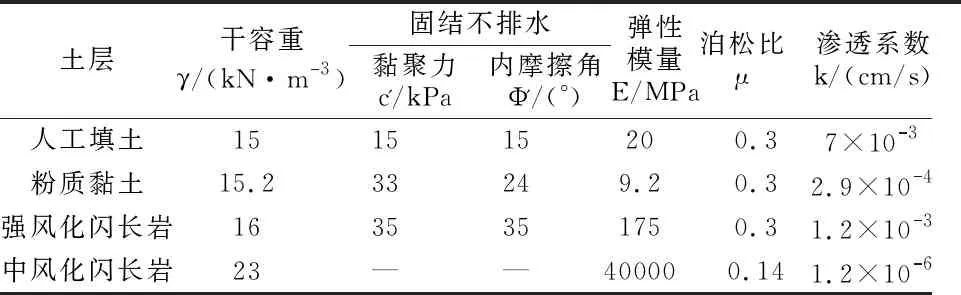
表1 土体材料

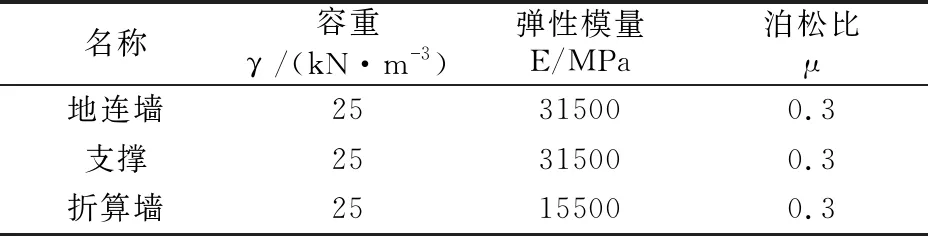
表2 弹性体材料

3.1.4 边界条件

在对称面上施加对称边界条件和对称水头条件，其余侧面约束水平方向位移和施加定水头边界，底面固定且不透水，上表面自由。

3.2 施工步序

按实际施工步骤概化的模型计算分析步见表3。

表3 计算分析步

3.3 计算结果分析

3.3.1 地连墙位移变形规律分析

场地水文地质条件独特，地下水效应显著，必须采用流固耦合方法对地连墙位移变形进行分析计算，地连墙各截面位置如图6所示，其中截面1、2、6的侧向位移是沿x轴方向的侧向变形，截面3、4、5是沿y轴方向的变形，截面3和5分别处于AO和OB的中点，向基坑坑内的变形的方向为正，计算结果如图7—图10所示。

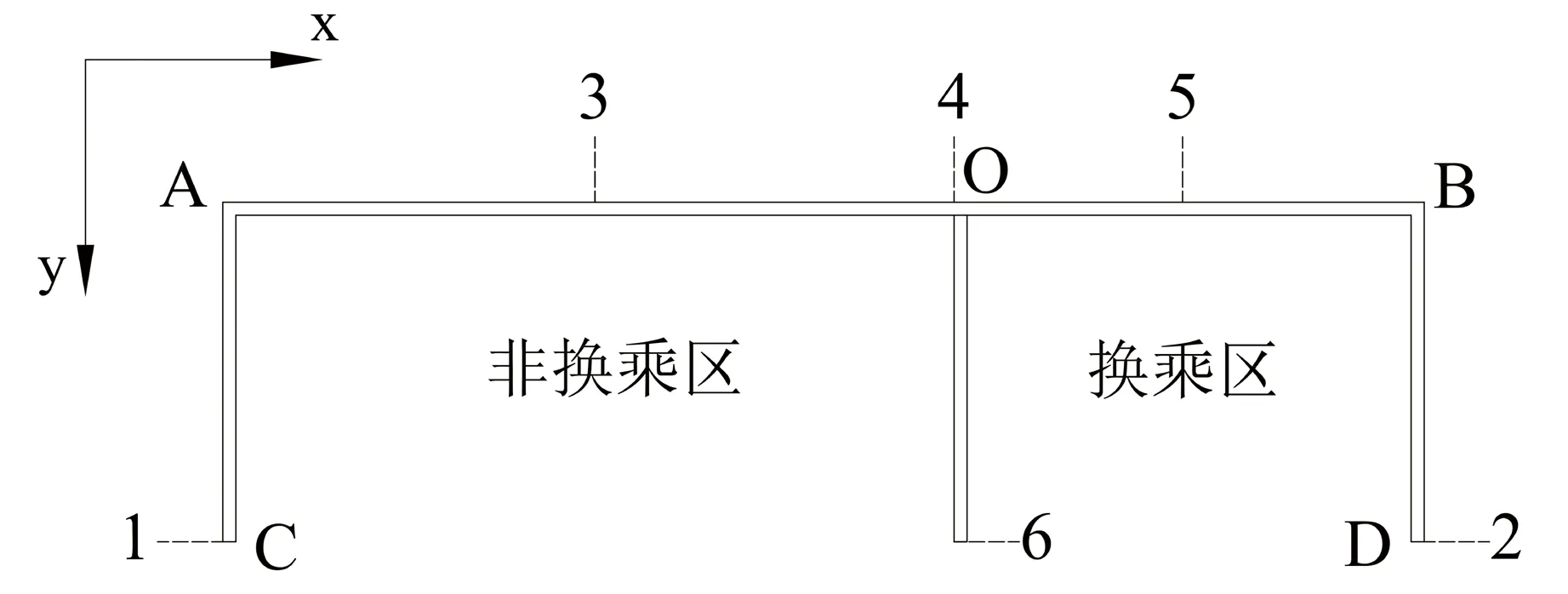
图6 截面位置示意图

(a)第5层开挖后；(b)第6层开挖后；(c)第7层开挖后；(d)第8层开挖后

图7为地连墙AB段内侧向位移云图，图8为截面3和5处地连墙侧向位移随开挖层数变化曲线。从图7中可以看出，在换乘区和非换乘区公共部分土层开挖完成后，墙体的侧向变形基本沿中心对称分布，中心点处变形最大，向两端逐渐减小。随着换乘区继续向下开挖，此时AO段的变形不再继续增加，如图8a所示；OB段的变形则继续增加，最大位移点位置不断下移，如图8b所示，当开挖完成后，整个AB段墙体的侧向变形不再对称分布，OB段墙体变形大于AB段，而在OB段，靠近O点的墙体变形大于靠近B点的，最大变形为17.6mm，在深度18m，长度65m的位置，该处变形随开挖层数变化曲线见图9。

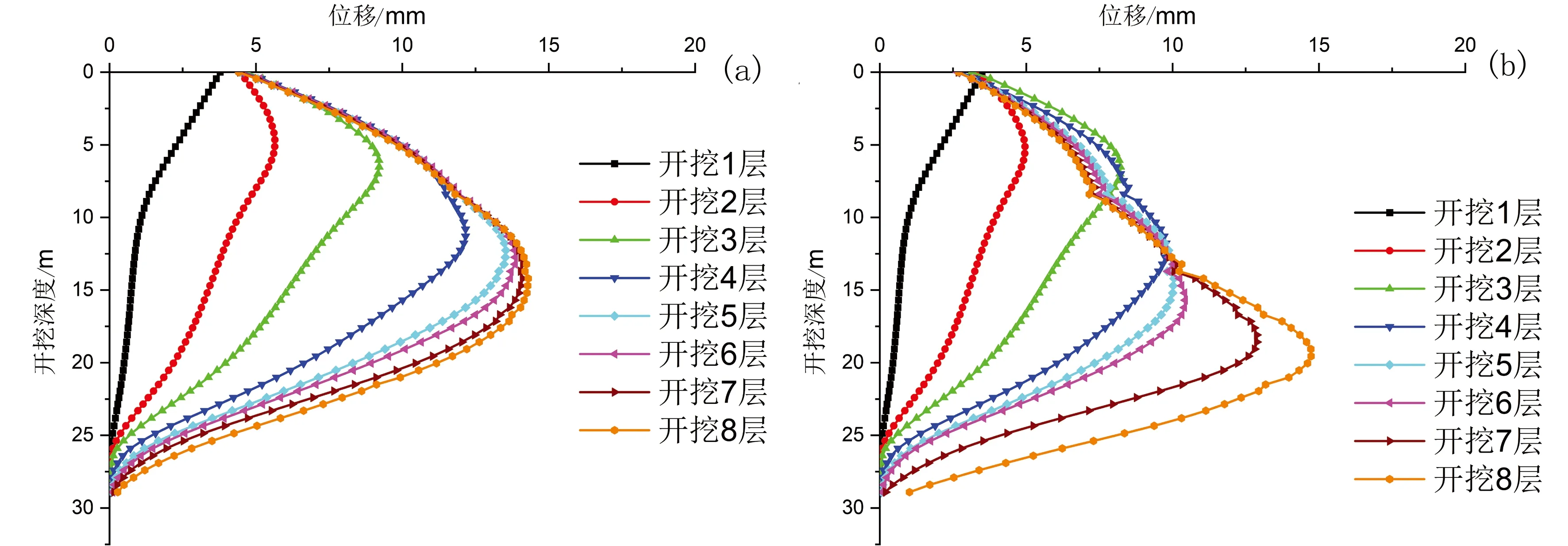
(a)截面3；(b)截面5

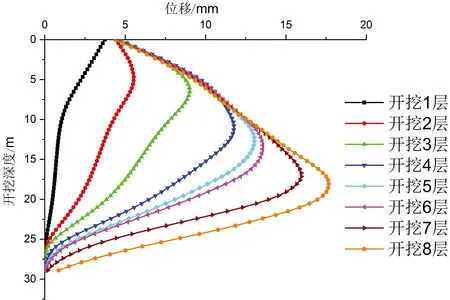
图9 地连墙AB段最大侧向变形

对于地连墙AC和BD段以及换乘区额外部分开挖前的AB段，其水平变形规律符合一般地连墙的变形规律，即边长中心处变形最大，向两边逐渐减小。由于模型的对称性，AC和BD段的最大侧向位移分别在截面1和2处，图10为截面1和2处地连墙侧向位移随开挖层数变化曲线。从图10可以看出，AC段处于非换乘区一侧，公共部分土层开挖完成后，墙体不再继续变形，最大侧向位移为18.3mm，在开挖深度11m处，而BD处于换乘区一侧，随着开挖深度的增加，变形继续增大，最大水平位移为22.9mm，在开挖深度18m处。

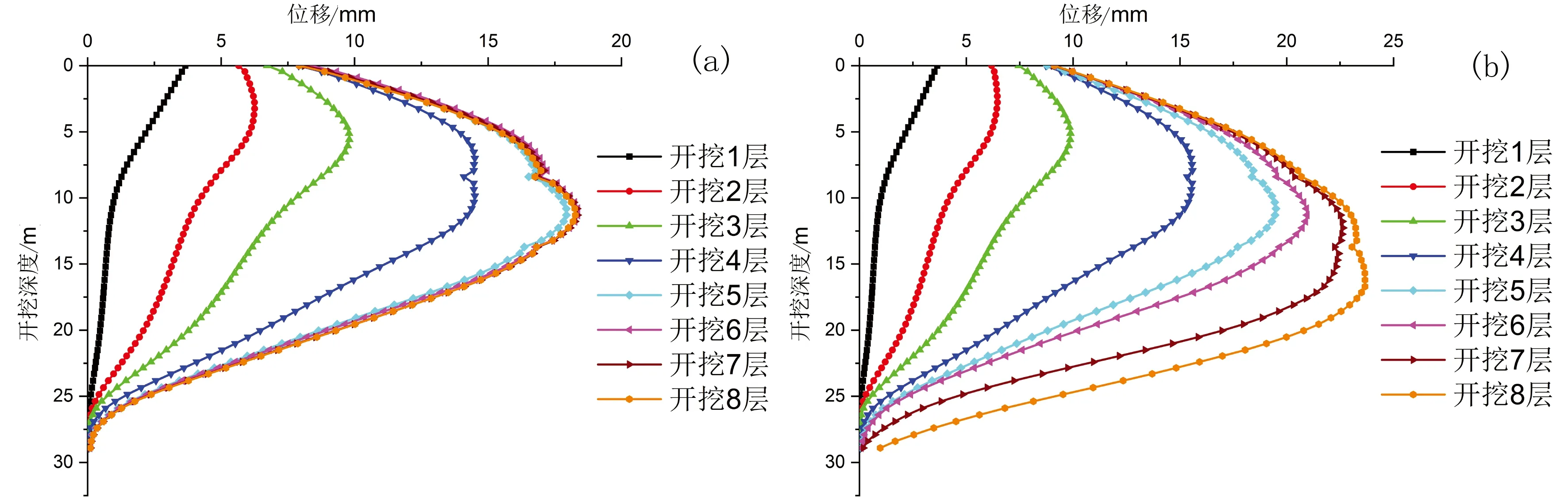
(a)截面1；(b)截面2

从图7—图10中可见，由于换乘站基坑开挖的特殊性，使得AB段地连墙的最大侧向变形不仅不在其对称轴，而且小于AC和BD段的最大侧向位移，这是由于换乘区和非换乘区中间的内部支护结构对AB段地连墙有支撑连墙作用，这种作用会减少与地连墙垂直相交处的地连墙位移变形，距离连墙越远，这种作用的效果越弱，因此AB段地连墙在换乘区的变形规律表现为变形从内部支护结构到地连墙短边先增大后减小，最大变形出现在内部支护与换乘区中点之间。同时在这种连墙支撑作用下，AC和BD段的地连墙最大侧向位移均大于AB段的最大侧向位移，表明地连墙最大侧向位移出现在短边而不是长边，这与一般基坑地连墙的变形规律相反[17-18]。

内部支护结构最大侧向变形在截面6处，随着开挖深度的增加，墙体侧向变形不断增大，最大为4.5mm，位于支护结构的顶端(图11)。

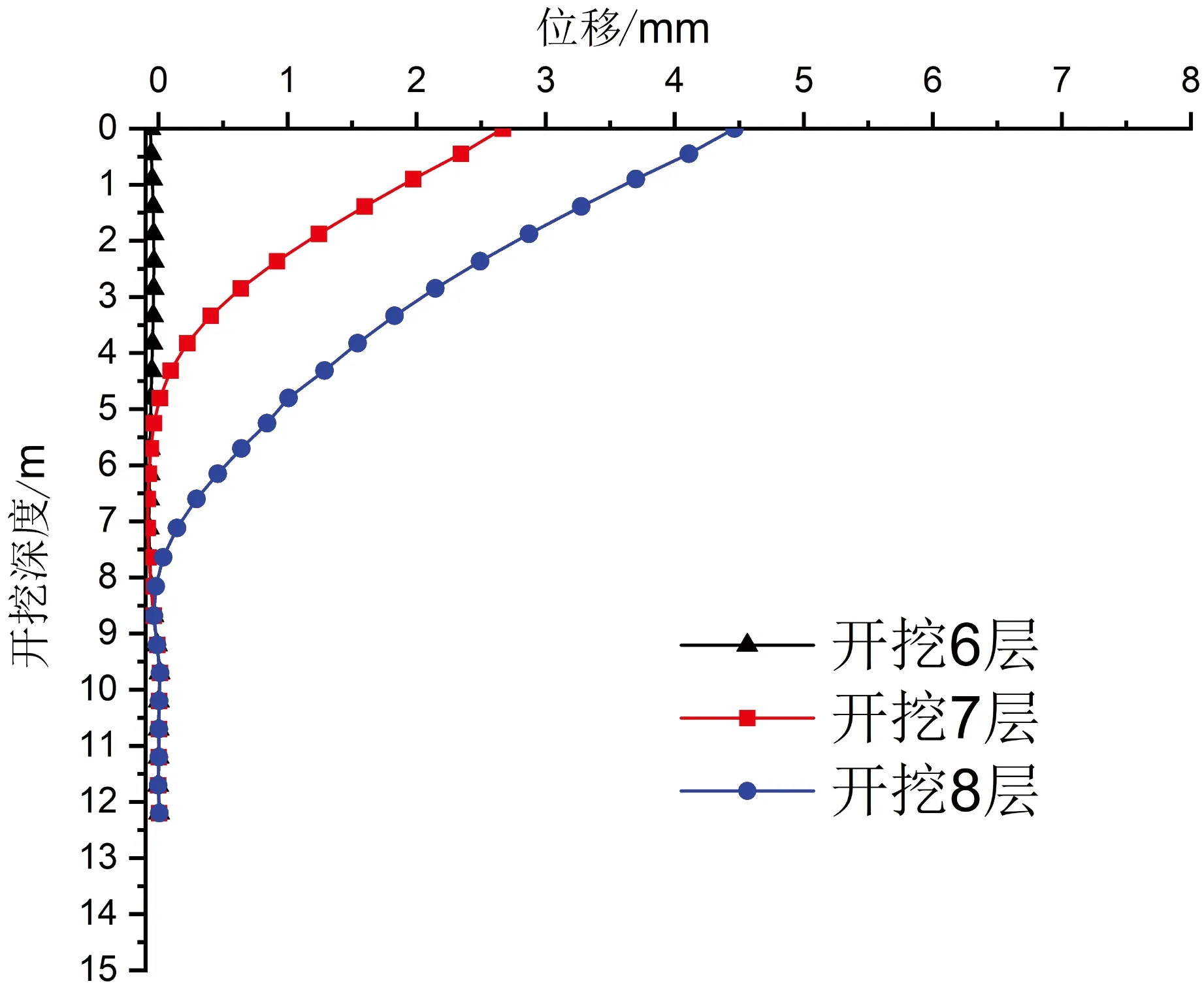
图11 内部支护侧向变形图

与外部地连墙的变形规律不同，折算墙的最大位移始终在顶端，墙体变形沿深度向下减少，这与桩支护结构变形规律相同[19-20]，表明(式5)的折算方法是合理的。

3.3.2 地面沉降发展规律

基坑开挖对地面的影响也是需要考虑的重要问题，图12为考虑流固耦合条件下基坑周围地面沉降计算结果。

图中地面沉降变化规律与地连墙变形规律类似，图12a表明在换乘区开挖前，基坑外围的地面沉降对称分布，图12b—图12d则表明换乘区开挖后，地连墙换乘区后的沉降量逐渐增大，整体不再对称分布，BD段墙后沉降大于AC段，OB段墙后的沉降大于AO段，墙后最大沉降出现在截面2处墙后7m的位置，约为15.9mm，墙后40m以内沉降曲线呈凹槽型，在40m以外沉降几乎不再变化。

4 结论

本文以济南长途汽车站地铁换乘站为研究对象，建立了考虑流固耦合的三维有限元模型，得到了基坑地连墙变形和周围地面沉降模拟结果。

(1)外部地连墙最大侧向位移出现在基坑换乘区一侧地连墙短边的中点，最大侧向位移为22.9mm，在开挖深度18m处；地连墙长边的变形规律表现为在换乘区和非换乘区公共部分的土层开挖阶段，墙体的侧向变形沿长边中心对称分布，中心点处变形最大，向两端逐渐减小，在换乘区继续开挖后，长边墙体在换乘区部分的变形从内部支护结构到短边先增大后减小，最大变形出现在内部支护与换乘区中点之间，为17.6mm，在深度18m位置。

(2)内部支护结构最大侧向变形在其长度方向的中心处，随着开挖深度的增加，墙体侧向变形不断增大，最大为4.5mm，位于支护结构的顶端；内部支护结构的最大位移始终在顶端，墙体变形沿深度向下减少。

(3)基坑周围地面最大沉降出现在换乘区一侧短边中心墙后7m的位置，为15.9mm；墙后40m以内沉降曲线呈凹槽型，在40m以外沉降几乎不再变化。