中国海域及邻区基于BP神经网络的矩震级转换模型

吴果 李建强 冉洪流 周庆 谢卓娟

1)中国地震局地质研究所，活动构造与火山重点实验室，北京 100029 2)中水北方勘测设计研究有限责任公司，天津 300222 3)应急管理部国家自然灾害防治研究院，北京 100085

0 引言

我国海域及邻区同时受到欧亚板块、西太平洋板块、印澳板块和菲律宾海板块的作用(图1)，构造活动强烈、地震频发(刘光鼎，1992；彭艳菊等，2008)。海域地震对我国沿海地区的经济建设和社会稳定以及我国的海洋资源开发构成了严重威胁(丁海平等，2011；谢卓娟等，2020)。因此，分析我国海域及邻区的地震活动特征并进行海域地震区划的重要性日益凸显(李小军等，2020)。区别于大陆地区，广大海域地区缺乏地震地质、地球物理等资料(林趾祥等，1999)，仪器地震记录成为分析我国海域地震活动性最重要的基础资料。

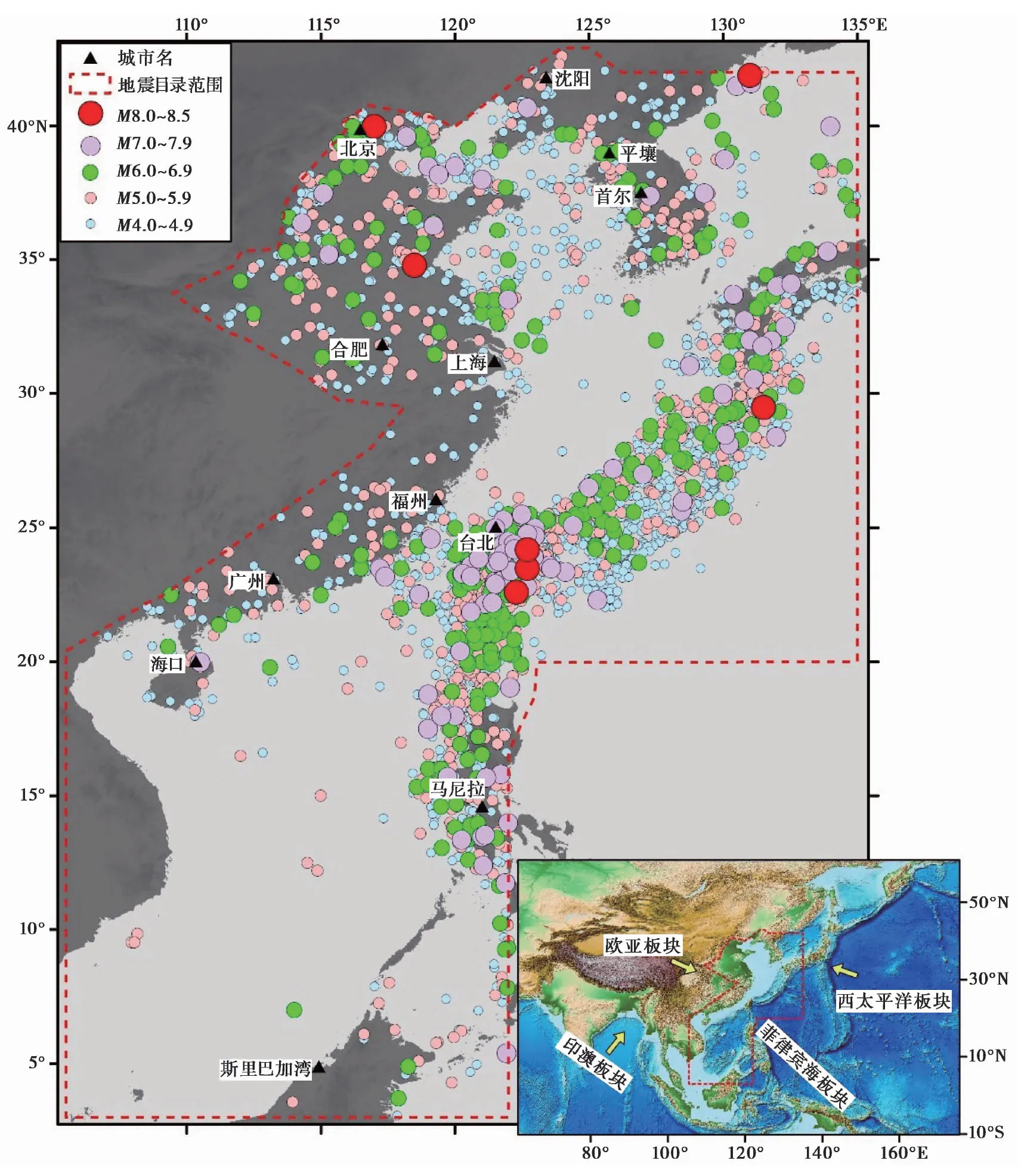
图1 中国海域及邻区震中分布(公元前1767—2020年9月)

地震震级是地震记录中最重要的参数之一，是通过测量地震波中的某个震相的振幅来衡量地震的相对大小的一个量(刘瑞丰等，2018)。由于不同类型震级基于的地震波类型和优势周期不同，使得不同震级标度之间存在一定差异。新的国家标准《地震震级的规定》(GB17740—2017)中规定了地方性震级(ML)、面波震级(MS)和矩震级(MW)等6种震级标度。由于矩震级具有与地震震源的物理过程直接关联、可以表征地震的绝对大小且不会产生震级饱和等优点，其已经成为国内外地震学界推荐优先使用的震级标度(陈运泰等，2004、2018)。

国际上最新的地震活动研究成果大都基于矩震级，例如适用于海域俯冲带的地震动衰减模型(Abrahamson et al，2016、2018；Kishida et al，2018a)。然而，由于矩震级的测定工作开展较晚、原理较复杂，历史地震和大量的早期仪器地震记录均缺乏矩震级记录。如果对其他类型的震级不加以处理，直接输入基于矩震级的模型，将会引起较大误差，影响计算结果的可靠性。因此，在地震活动分析和地震危险性评价领域经常需要开展震级转换的工作，与其相关的研究一直是国际上的研究热点(Pandey et al，2017；Kishida et al，2018b；Konstantinou et al，2018；Lolli et al，2018、2020；Wu et al，2019；Kumar et al，2020；Das et al，2021；Manzunzu et al，2021)。

已有学者拟合了国内不同震级标度之间的转换关系(刘瑞丰等，2007；汪素云等，2009；Wu et al，2019)以及中国地震台网震级标度与国际上相应测定震级之间的关系(刘瑞丰等，2005、2006；Bormann et al，2007、2009)。同时，由于面波震级是国内工程地震学界最常用的震级标度(肖亮，2011；潘华等，2013；Xu，2019；Xu et al，2021)，多位学者使用最小二乘回归或正交回归建立了MS到MW的转换关系，例如陈宏峰等(2014)基于2008年以来中国地震台网86个5.3级以上地震数据，采用正交回归拟合了MS与MW的转换关系；Cheng等(2017)采用正交回归拟合了中国大陆及邻区MS与MW的分段线性关系；沙海军等(2018)使用加权最小二乘回归建立了中国地震台网MS与MW的统计关系。这些研究成果在地震预测预报、工程抗震、防震减灾等领域发挥了重要的作用。

区别于中国大陆地区，海域地震具有分布范围广、震源深度变化大以及地震监测水平相对较差且空间差异大等特征。因此，海域地震的经纬度范围和震源深度等均可能影响到MS与MW的对应关系。然而，前人对于MS到MW的转换关系的研究大都围绕中国大陆地区进行，目前尚缺少以我国海域及邻区为研究区的针对性研究，仅谢卓娟等(2020)在编译我国海域及邻区的地震目录时拟合了MW到MS的线性关系。此外，目前国内外常用的拟合震级转换关系的方法主要为最小二乘回归和正交回归(Castellaro et al，2007；Wason et al，2012；吴果等，2014；Cheng et al，2017；Xie et al，2021)。这2种方法通常仅考虑单因子MS，未能考虑诸如震源深度等因素对结果的影响，且当数据点偏离线性规律时拟合效果受到影响。

近年来，BP神经网络已经被成功应用于地震滑坡预测、地震波震相识别等地震学相关领域(孙印等，2018；Tian et al，2019；张彭达等，2020)。相比于传统的线性拟合，BP神经网络可以建立多种影响因子与目标参数之间的非线性映射，这为建立震级转换模型提供了新的探索思路。本文以中国海域及邻区为研究区，收集了最新的MS与MW地震记录数据。从中提取年份、深度、MS等多个因子，进而训练BP神经网络建立以MW为目标震级的震级转换模型。同时，采用最小二乘回归和正交回归拟合了MS与MW的线性转换关系以作为参考。通过分析误差大小和残差分布，对3种算法进行了系统的对比分析。本研究可以用于建立新的同时考虑多种因素的震级转换模型，为编译我国大陆或海域统一震级标度的地震目录提供参考。

1 地震资料

谢卓娟等(2020)新编录了中国海域及邻区的地震目录，时间跨度从公元前1767年至2018年10月。该目录汇集了中国大陆、中国台湾以及日本、韩国、菲律宾等国家和地区的地震数据，是目前数据收集最为完整的中国海域及邻区的地震目录。由于编制海域地震区划图时需要考虑远场大震的影响，因此该目录的数据收集范围不仅包含渤海、黄海、东海和南海等主要海域，还囊括了中国大陆沿海的地震区带(图1 中红色虚线框)。

由于谢卓娟等(2020)的地震目录的截止日期为2018年10月，且近年来有大量新增的矩震级记录可供收集(Di Giacomo et al，2021)。因此，本文在上述地震目录的基础上，进一步收集中国地震台网(1)https://data.earthquake.cn/和国际地震中心(2)http://www.isc.ac.uk/iscbulletin/的地震数据，数据收集时间范围为公元前1767—2020年9月(图1)。国际地震中心的地震目录收录了全球主要国家的多种震级标度的仪器地震记录，其中包含全球矩心矩张量(Global Earthquake Moment Tensors project，GCMT)的矩震级记录。GCMT的矩震级记录是目前国际上最权威、数据量最大的矩震级数据来源(Di Giacomo et al，2021)，并且与中国地震台网中心测定的矩震级基本一致(陈宏峰等，2014)。因此，本文选择GCMT的矩震级作为震级转换的目标震级，下文的矩震级特指GCMT的矩震级。

从收集的地震数据中共提取到中国地震台网的面波震级和GCMT的矩震级同时存在的地震记录1480条。地震记录的时间跨度自1988年1月至2020年9月，地震数呈逐年递增趋势。面波震级的分布范围从MS4.0～7.9，矩震级的分布范围为MW4.6～7.7。以0.5个震级单位将矩震级分档，不同震级档对应的地震数如下：MW4.6～4.9地震292个、MW5.0～5.4地震751个、MW5.5～5.9地震304个、MW6.0～6.4地震105个、MW6.5～6.9地震18个、MW7.0～7.4地震9个、MW7.5～7.7地震1个。地震数据主要分布于琉球海沟俯冲带、中国台湾地区以及马尼拉海沟俯冲带，仅有10条数据位于中国大陆沿海或近海地区。

2 地震数据预分析

区别于MS到MW的线性关系模型，BP神经网络可以同时输入多个影响因子。因此，首先对地震目录做预分析以确定影响因子。借鉴前人的研究(Cheng et al，2017；林彬华等，2019)，同时考虑到海域地震分布区域广、深度范围大等特征，确定了年份、深度、经度、纬度、面波震级等5个影响因子。通过观察矩震级和面波震级的震级差(MW-MS)随这5种影响因子的变化(图2)，可以定性地认识这些影响因子的作用。

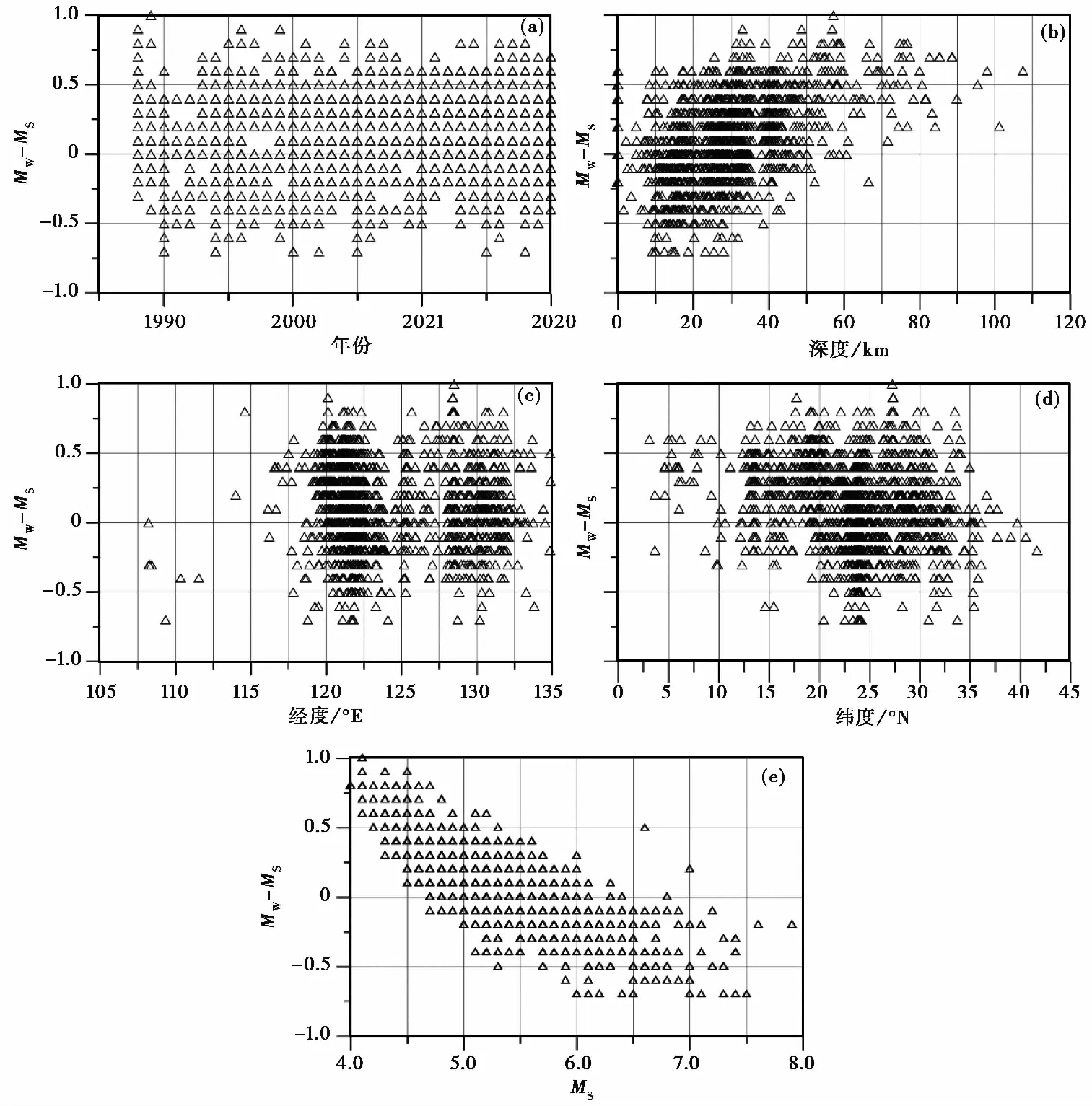
图2 不同影响因子与矩震级和面波震级震级差(MW-MS)关系图

图2显示，随着年份增大，震级差未呈现明显的分布规律，仅在少数年份时分布范围有所收缩(如2012年)，这说明该因素对震级差的影响较小。随着经度和纬度变化，震级差呈现较为复杂的分布趋势，经纬度对震级差的影响总体上比年份显著。随着深度增大，震级差总体上由负值过渡到正值，这说明深度因子的影响十分明显并具有一定的规律性。面波震级对震级差的影响最为直观和显著。当面波震级由MS4.0增加到MS6.5时，震级差由正值过渡到负值，样本点的中心线呈近似线状分布。当面波震级大于MS6.5时，震级差的绝对值不再线性增大，MS7.5以上的2个数据点的震级差甚至出现显著减小，这提示传统的二元线性模型很难兼顾震级差在大、小地震之间的变化趋势。以上分析说明5个因子均对面波震级与矩震级之间的对应关系有一定影响，但影响的显著程度和方式存在差异。将上述有影响的因子同时纳入考虑，有利于提高震级转换模型的精度。

3 BP神经网络

人工神经网络(Artificial Neural Network，ANN)是模拟和抽象人类大脑神经的思维活动的一种机器学习算法，其通过大量简单神经元广泛链接而形成复杂的神经网络(Kros et al，2006)。ANN具有非线性映射、自学习、自适应以及强泛化等优点，可以处理并存储不精确的和模糊的数据，近年来已在地震滑坡预测(Tian et al，2019)、地震波震相识别(孙印等，2018；王钰清等，2019；张彭达等，2020)、地震震源破裂面参数估算(Asim et al，2019)等地震学相关领域取得成熟的应用成果。

本文采用的BP神经网络为误差反向传播(Back Propagation，BP)神经网络，是一种经典的人工神经网络，被广泛应用于地震预测、地震震级修正等(蒋淳等，1994；王炜等，2000；项月文等，2015；蔡润等，2018；林彬华等，2019；袁爱璟等，2021)。BP神经网络结构一般由输入层、输出层和若干隐含层组成(图3)。对于本研究，基于前文对地震数据预分析的结果，输入层中包含年份、深度、经度、纬度、面波震级共5个影响因子，输出层中仅包含1个神经元，对应模型估算的矩震级值，隐含层的层数和每层包含的神经元个数则需要通过对比不同参数设置下模型的表现来确定。经过反复调试，发现当隐含层拥有2层神经网络、每层分别包含3个和4个神经元时(图3)，模型的表现达到最优。隐含层中各个神经元均有相应的权值，权值的优化通过输入数据对模型进行训练来实现。

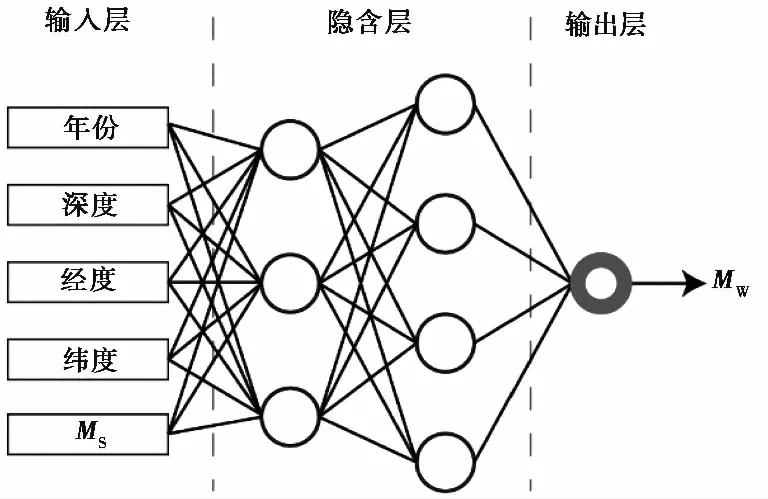
图3 本研究采用的BP神经网络结构示意图

每当选定一种BP神经网络结构，即可以对模型进行训练：首先从收集到的数据中选取部分数据作为训练样本，每个训练样本均包含年份、深度、经度、纬度、面波震级共5个影响因子和实际记录的矩震级值。BP神经网络的训练过程包含2个传播过程，分别为信号的正向传播和误差的反向传播(蔡润等，2018)。信号的正向传播是将训练样本中的5个影响因子输入到输入层(图3)，然后经过隐含层的逐层处理并最终到达输出层。将输出层中得到的矩震级估计值与实际记录的矩震级值进行对比，即得到拟合误差。将误差逆向输入隐含层并修正隐含层中神经元权值的过程即误差的反向传播过程。信号的正向传播和误差的反向传播可以通过更新训练样本循环往复进行，直到得到理想的误差最小值。在此过程中，隐含层的神经元权值被不断优化，最终使模型达到逼近输入和输出之间的非线性映射的目的(冯利华，2000)。

模型训练好后，需要进一步评估该参数设置下模型的表现。将收集的数据中未被划入训练样本的数据作为测试样本，每个测试样本中同样包含上述5个影响因子和实际记录的矩震级值。将测试样本的5个影响因子输入训练好的模型，直接计算出矩震级的估算值，将估算值与实际值进行对比即可评价模型的表现。上述过程为信号的一次性正向传播过程，不再涉及误差的反向传播和神经元权重的更新。

4 转换结果及误差分析

为了保证对模型结果评价的合理性，本文采用了机器学习领域常用的多重交叉验证的方法(Asim et al，2019)。以本文采用的10重交叉验证为例，将1480个样本随机划分为10等份，每次以其中9份作为训练样本建立模型，以剩余的1份作为测试样本检测模型的预测效果，从而保证每次训练样本和测试样本之间互不重叠，最终评价结果取10次测试的均值。

4.1 转换结果

为客观评价BP神经网络的震级转换表现，本文借鉴前人的做法，采用最小二乘回归和正交回归拟合了MS到MW的线性转换公式，以此作为参考。前人已详细介绍了最小二乘回归和正交回归的原理(Cheng et al，2017；沙海军等，2018；Xie et al，2021)，本文不再赘述。二者的拟合结果如下

最小二乘回归

MW=2.089+0.620×MS

(1)

正交回归

MW=1.853+0.666×MS

(2)

图4展示了BP神经网络、最小二乘回归和正交回归3种算法的转换结果。最小二乘回归和正交回归拟合的直线较为接近。在MS5.0～6.5区间，二者近似位于数据点中线；在该区间以外，二者均逐渐偏离数据点中线，尤其是在MS6.5以上的大震端，二者均明显低估。由于正交回归的斜率略大，因此其在大震端的表现要优于最小二乘回归，这与前人的研究一致(Castellaro et al，2006)。BP神经网络的转换结果总体上随着真实记录的数据点的变化而变化，在大震端的分布明显优于最小二乘回归和正交回归。

图4 不同算法的震级转换结果图

4.2 误差分析

采用平均绝对误差(Mean absolute error，MAE)和均方根误差(Root mean squared error，RMSE)对3种算法的表现作进一步定量评估。MAE和RMSE的定义分别如下

(3)

(4)

式中，MW，预测i为矩震级的预测值，MW，实际i为矩震级的实际记录值，n为样本量。表1 显示，最小二乘回归的MAE和RMSE略小于正交回归，但比BP神经网络的相应值高40%左右。因此，BP神经网络在MAE和RMSE上的表现明显优于最小二乘回归和正交回归。

表1 不同算法震级转换结果的误差对比(均采用10重交叉验证)

进一步分析3种算法的残差绝对值(|MW，实际-MW，预测|)的频度分布(表2 和图5)。在1480个样本中，BP神经网络的残差绝对值有一半以上在0～0.1之间，有2个样本位于0.5～0.6之间，没有样本落入更大的残差绝对值范围。最小二乘回归和正交回归的残差绝对值更多地位于较大的区间，分布更离散，同时最大值达到0.9或1.0。因此，3种算法中BP神经网络的残差绝对值更小，分布更集中。

表2 不同算法震级转换结果的残差绝对值频度分布

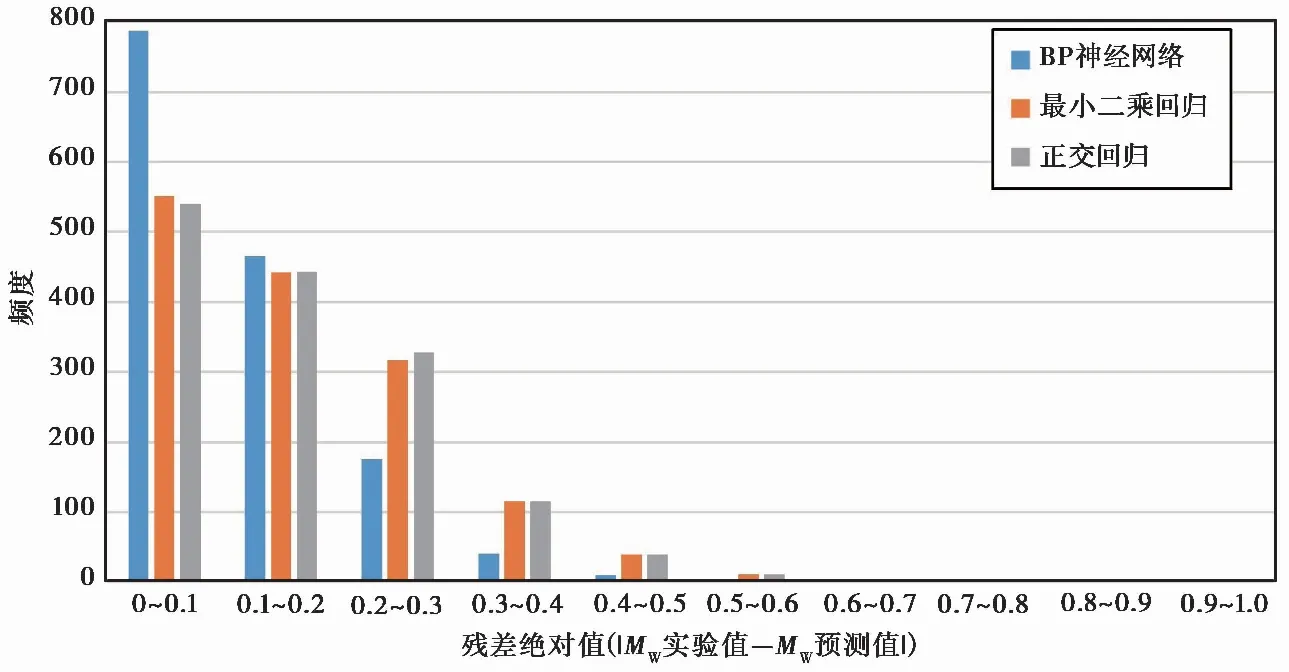
图5 不同算法震级转换结果的残差绝对值频度分布

最终观察3种算法下不同震级档的MW实际值对应的残差绝对值的均值分布(表3)。在所有震级档内，BP神经网络的残差绝对值的均值都更小，并且这种优势在MW6.5以上时更为显著。当震级MW≥7.0时，BP神经网络的残差绝对值的均值分别比正交回归法和最小二乘回归法小0.2和0.3左右。

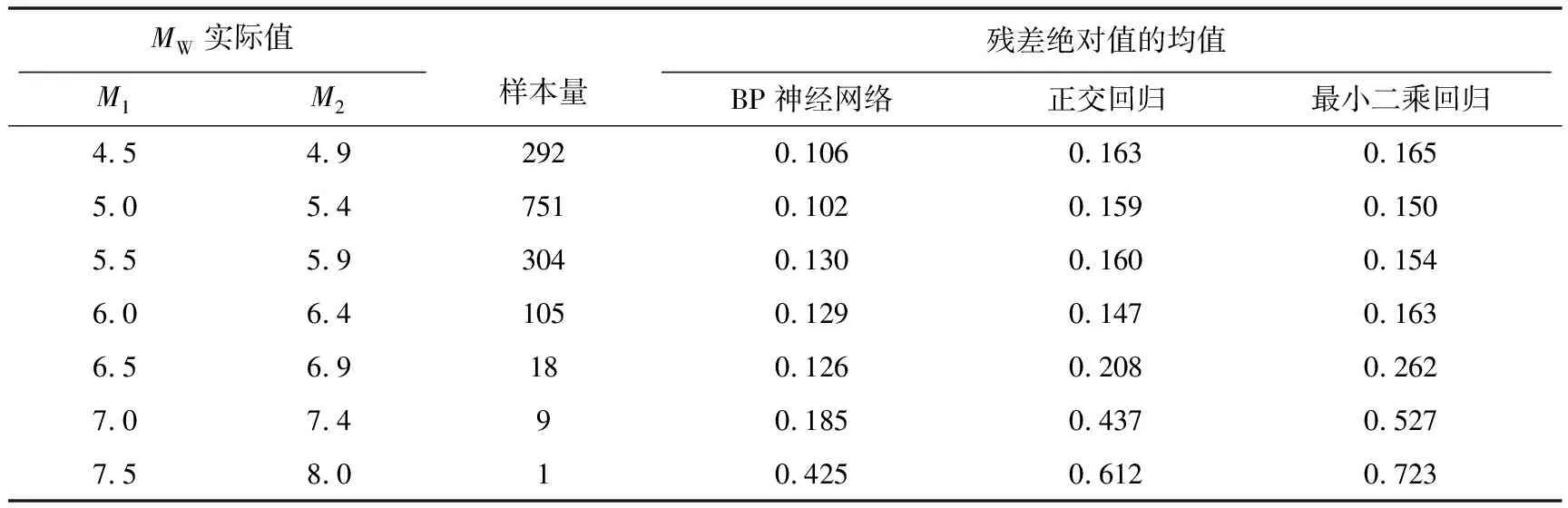
表3 不同震级档的MW实际值对应的残差绝对值的均值分布

5 结论

综合前文所述，本文主要结论如下：

(1)在谢卓娟等(2020)编译的中国海域及邻区的地震目录的基础上，进一步收集数据，共获得中国地震台网的面波震级和GCMT的矩震级同时存在的地震记录1480条。

(2)从收集的数据中提取年份、深度、经度、纬度、面波震级共5个影响因子，以实际的矩震级记录值为标记，训练BP神经网络建立了以GCMT的矩震级为目标震级的转换模型。

(3)通过将BP神经网络与最小二乘回归和正交回归的线性模型进行对比发现，BP神经网络的转换结果的总体分布趋势更接近真实地震记录。在不同震级档下BP神经网络的残差绝对值的均值都更小，当震级为6.5以上时优势增大。

(4)最小二乘回归和正交回归的转换结果较接近，在大震端，正交回归的结果稍优于最小二乘回归。当震级≥6.5时，二者均出现较明显的低估。

(5)相比于最小二乘回归和正交回归的线性模型，BP神经网络的平均绝对误差和均方根误差更小，且残差绝对值更集中地分布于小值范围。

(6)BP神经网络在震级转换上显示出良好的应用前景，有望为编制我国统一震级标度的地震目录提供参考。