圆角对压裂泵曲轴应力影响分析
◇长江大学机械工程学院 王江伟 韩玮栋 肖 昱
利用ANSYS Workbench对2800型压裂泵曲轴进行有限元分析,研究了实际工况下曲轴的应力分布。通过分析阶梯型圆角结构的尺寸与曲轴最大应力的关系,得出随着圆角尺寸r的增大,曲轴最大应力曲线呈现出先降低后增大的趋势;随着圆角尺寸h的增大,曲轴的最大应力呈现先降低后增高的趋势,且在h大于3.5mm以后应力值趋于平缓,从而得到阶梯型圆角的最优尺寸,对比普通圆角结构曲轴,阶梯型圆角结构明显地优化了曲轴的应力。
压裂泵是油田开采石油的重要压裂设备。由于压裂技术的广泛使用,不仅增加了油井的开采量,大大加快了油田开发的步伐,而且大幅度地提高了石油的产量。所谓压裂,就是将液体通过压裂泵产生高压。然后将压裂液体打入岩层,使岩层发生破裂,形成数条的油层裂缝,减少石油的流动阻力,从而方便石油向着套管流动,从而实现提高油井的生产能力和达到增产增量的目标。作为压裂泵动力端的关键部件,曲轴在整个压裂过程中起着将低压流体转化为高压流体的关键作用[1]。
本文通过以2800型压裂泵的曲轴为研究对象,对曲轴进行受力分析,借助有限元软件ANSYS Workbench对曲轴进行有限元分析,并且通过对其结构上的应力分布分析,对曲轴在尺寸上进行优化,使曲轴自身的应力分布上更加的合理,从而为合理设计曲轴提供依据,为油田研发高效泵提供了理论参考和技术支持。
1 压裂泵的工作载荷分析
2800型压裂泵的动力端传动形式为曲柄滑块机构,通过改变运动形式将圆弧齿轮的旋转运动转化为柱塞的直线往复运动。本压裂泵为为5缸单作用往复柱塞泵,整根曲轴上承受相位差为144°的五个连杆力、主轴承支座反力、自重和偏心质量力的作用。假设各作用力均为集中载荷,连杆对曲轴的力为主要的作用力,其他力相对较小可以忽略不计。所以在分析曲轴的作用力时,只分析连杆对曲柄的作用力。
在进行载荷分析时,可以对曲轴做出以下假设[2]:
(1)连杆力集中作用在曲柄销的轴线中点。
(2)在整个工作过程中,认为曲轴箱和轴承支座不发生弹性变形。
2 曲轴的有限元分析
2.1 材料参数
曲轴的材料为40CrNiMoA,其强度极限为1048MPa,屈服极限为836MPa,弹性模量E=206GPa,泊松比μ=0.3。
2.2 有限元模型及网格划分
利用三维建模软件solidworks建立曲轴三维模型,将曲轴模型完成后导入到ANSYS Workbench中,在划分网格时对连杆轴颈和主轴颈过渡圆角处进行网格加密,整体曲轴采用四面体单元solid186,共有121919个节点,75016个单元有限元,模型如图1所示。

图1 曲轴有限元模型
2.3 载荷处理与边界条件
(1)载荷处理。对于每个曲柄的载荷,假设其作用在轴径上的压力合力为Fc。根据有限宽度轴径油膜应力分布规律,并忽略有孔处压力峰值突变的影响,其分布规律为:压力qx沿 着曲轴轴颈按二次抛物线规律分布;沿着轴径圆周方向120°范围内按余弦规律分布。
建立如图2所示的空间直角坐标系,可以求得曲轴轴线方向上压力分布曲线方程为:
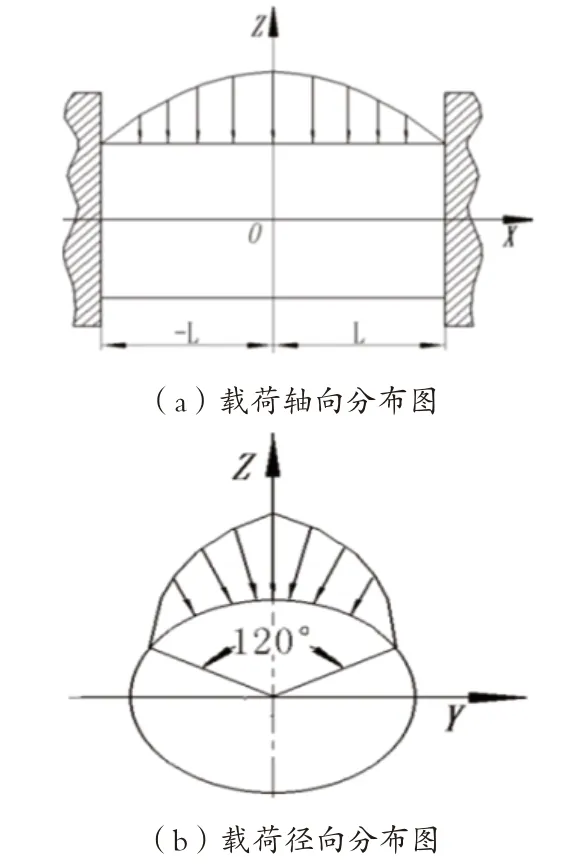
图2 曲轴的受力
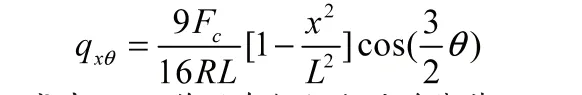
式中:Fc-作用在轴径上的总载荷,kN;R-曲轴的圆周半径,mm。
(2)边界条件处理。由于曲轴是通过圆弧齿轮从两端输入,并且通过轴承来进行轴向定位。则在每个曲柄端面施加径向约束,在连接轴的键槽的一个端面施加与曲轴旋转方向相反的周向约束,在两端面位置施加轴向约束[3]。
2.4 结果与分析
有限元分析的结果如图3所示,可知曲轴的最大应力位于曲轴轴颈部位,特别是曲轴轴颈与曲轴臂交界处,最大应力为558MPa。这是由于在曲轴的轴颈部位存在着周向的最大应力(处于余弦的峰值处)。由于几何尺寸的关系,在曲轴颈与曲轴臂连接处应力集中,因此曲轴的强度需要改进,且对强度的改进要从圆角的优化开始。

图3 普通圆角结构的曲轴应力分布
3 圆角对曲轴应力的影响
曲轴的结构优化如下所示。
对于有限元分析存在的应力集中问题,主要原因是由于曲轴臂和曲轴颈的几何尺寸相差较大,所以可以通过设置过渡段来避免过大的应力集中。为了保证曲轴设计的合理性,通过改进圆角结构是优化曲轴应力的一种行之有效的方式。由于应力集中往往出现在结构发生突变的位置[4],而如图4所示阶梯形圆角结构阶梯式的结构对轴颈位置的结构突变起到了一定的缓和作用。
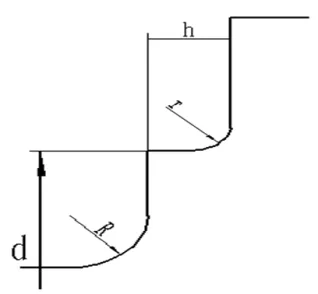
图4 阶梯型圆角
对于阶梯型圆角,除了R与普通圆角相同外,圆角尺寸r、h、d均不确定。为了研究阶梯型圆角参数对曲轴结构应力的影响,利用有限元方法对各参数定量分析得出应力变化情况。根据曲轴轴颈尺寸、机体尺寸以及两者之间的配合等得出圆角尺寸参数取值范围:r,2.5~9.5mm;h,1~5mm;d,184~202mm。当一个值变化时,其他参数取值为r=4.5mm,h=5mm,d=194mm。
(1)圆角尺寸r对曲轴应力的影响。如图5所示圆角尺寸r与曲轴应力的关系。随着圆角尺寸r的增大,曲轴最大应力曲线呈现出先降低后增大的趋势。各个变化过程中在r=2.5mm是取得最大值为547MPa,在r=6.5mm处取得最小值为430MPa。均小于结构为普通圆角时的最大等效应力558MPa。
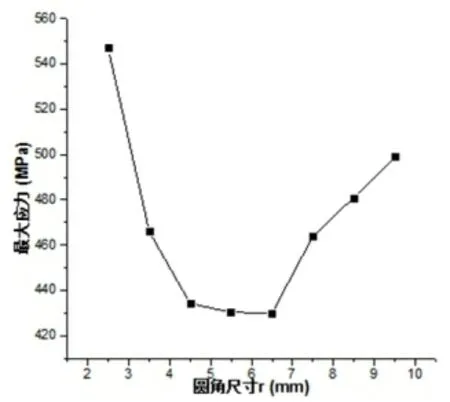
图5 圆角尺寸r与曲轴最大应力关系
(2)圆角尺寸h对曲轴的应力的影响。如图6所示圆角尺寸h与曲轴应力的关系。从图5得知,随着圆角尺寸h的增大,曲轴的最大应力呈现先降低后增高的趋势,且在h大于3.5mm以后应力值趋于平缓。在h=3.5mm处的应力值最低,大小为428MPa,在h=1处的应力值最大,大小为537MPa,由此可知,h无论取多大数值,最大应力都低于普通圆角结构的曲轴的最大应力。
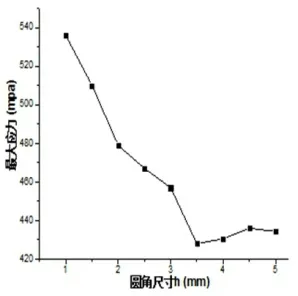
图6 圆角尺寸h与曲轴最大应力关系
(3)圆角尺寸d对曲轴的应力的影响。同样从图7得知,随着圆角尺寸d的增加,曲轴的最大应力先降低后增大,在d=194mm处取得最小值433MPa,在d=184mm处取得最大值522MPa,均小于普通圆角结构的曲轴的最大应力558MPa。
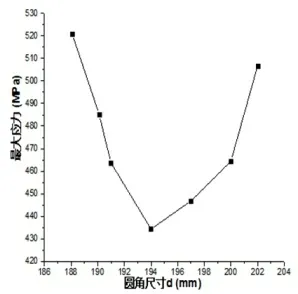
图7 圆角尺寸d与曲轴最大应力关系
由此可以确定阶梯型圆角结构的曲轴的最优尺寸为d=194mm,h=3.5mm,r=6.5mm。经过有限元分析计算得到的曲轴最大应力为424.4MPa。相对于普通圆角结构曲轴的最大应力下降了24%,优化效果比较显著。
4 结论
通过对2800型压裂泵曲轴有限元分析,得出以下结论。
(1)普通圆角结构的曲轴的应力最大的位置是曲轴臂和曲轴颈的交界处,即曲轴轴颈的圆角位置处,且最大应力值为558MPa,且远高于其他位置。所以在研究曲轴应力时主要考虑圆角位置的应力,在研究曲轴强度优化改进时主要从主轴颈圆角入手。
(2)对阶梯型圆角曲轴结构参数进行了定量分析,利用有限元方法分析阶梯型圆角各尺寸与曲轴最大应力的关系进行,得出最优的阶梯型圆角尺寸为d=194mm,h=3.5mm,r=6.5mm,优化后的曲轴最大应力为424.4MPa。
(3)对比普通圆角结构曲轴和阶梯型圆角结构曲轴,阶梯形圆角结构对曲轴应力的改进起到明显得的作用,显著降低了曲轴的应力。

