输电线路脱冰跳跃研究进展

蔡萌琦， 杜 洋， 周林抒， 陈小平， 郑鸣宇， 刘 静， 丁顺利

(1.成都大学建筑与土木工程学院， 成都 610106； 2.国网四川电力能源综合服务公司， 成都 610016；3.成都大学机械工程学院， 成都 610106)

输电线路在覆冰情况下具有复杂的受力状态，若技术方案采用不当，会导致导线、线夹和间隔棒甚至杆塔的破坏等恶性事故，威胁电网安全运行。中国许多地区处于山区，气象条件非常复杂，覆冰引起的电网事故时有发生，若由此引起电网系统性事故，将会对其社会生活产生极大影响，如表1所示。输电线路脱冰跳跃是指冰区输电线路的覆冰在温度等自然条件下脱落引起导线的上下振动，工程中称为“脱冰跳跃”。脱冰跳跃中各相导线之间及导地线之间的间隙可能小于相应的绝缘间隙，从而导致闪络、烧伤甚至烧断导线等电气事故[1-3]。目前，对于输电线路脱冰跳跃问题的研究主要采用实验、数值模拟和简化理论算法三种方法。

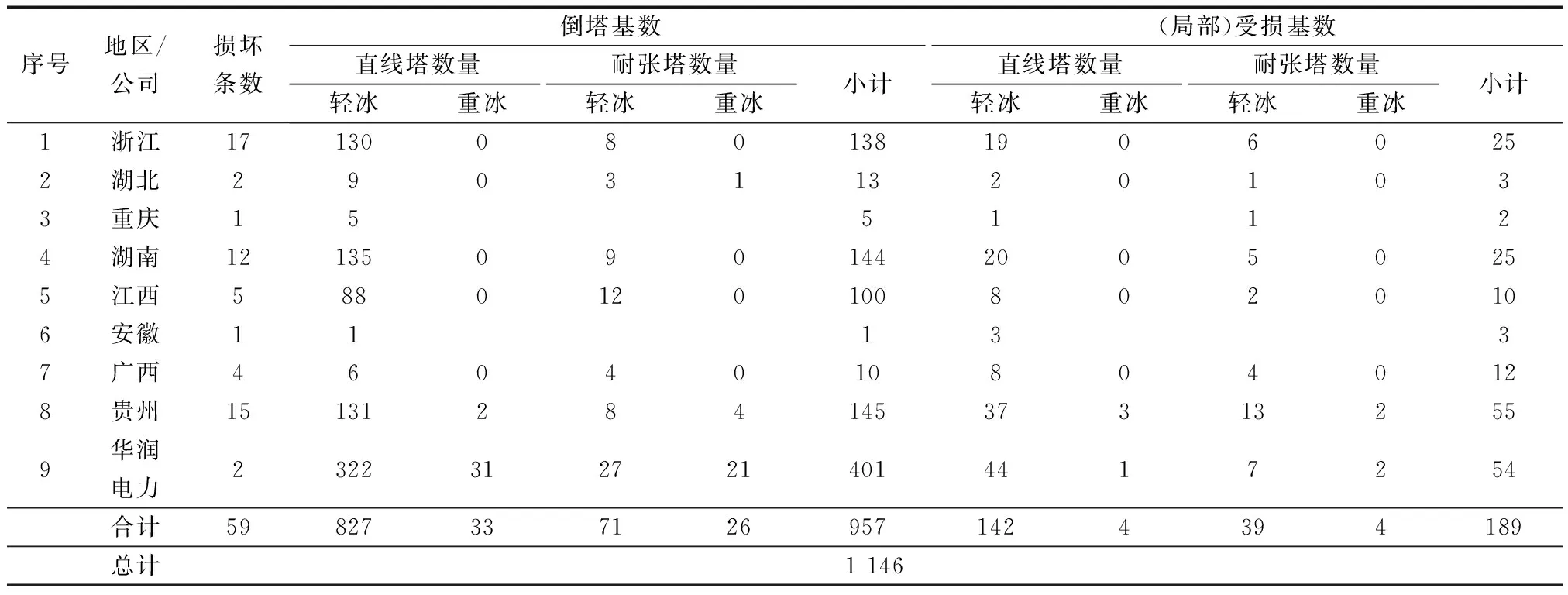
表1 2008年冰灾500 kV输电线路倒塔及受损情况Table 1 Tower collapse and damage of 500 kV transmission line during ice disaster in 2008

1 模拟试验

导线的覆冰脱落研究，其常用研究方法有三种：现场实测、模型试验、数值仿真模拟。其中现场实测的难度较大，因此该方法并不常见。中国有不少学者采用过模型试验的方法。最早在20世纪50年代就有学者利用静荷载模拟导线脱冰[4-5]，后来国际上也有许多学者基于此方法展开了深入研究。

这些学者的研究可推广到相同类型的输电导线，但当输电导线类型和分布在导线上的荷载发生变化时，这些研究结果的有效性还有待商榷。

Mogran等[6]早在1964年就对132 kV五档输电线路进行了在档距中点释放集中质量来模拟导线脱冰的试验，同时对冰跳高度进行了测量。Savadjiev等[7]在实验室里用3.22 m长的导线，对不同脱冰情况进行了模拟实验，同时测量了在导线脱冰时的最大上升高度、不同挂点间的张力变化情况及绝缘子串的偏转角度和位移等。中国首次开展对覆冰导线脱冰研究的是陈勇等[8]，其研究方法与Mogran等[6]类似，通过在导线上悬挂集中荷载代替导线覆冰，该研究同时还利用计算机仿真对脱冰工况进行了数值模拟，对比了试验结果和计算结果，对比结果表明两者的规律相同，数值也相近。

近年，学者们通过数值仿真模拟的方法对导线脱冰动力响应做了大量研究。谢献忠等[9]设计了缩尺比为1∶20的两档塔线体系实验模型。模拟了拉链式脱冰和同时脱冰、整档脱冰和局部脱冰等六种工况，并得到整档脱冰是最危险的一种工况、整档脱冰的最大跳跃高度可达跨度的2.02%等结论。此实验是在理论研究的基础上，以湖南220 kV的输电线路为原型而设计的，具有较好的实际工程参考价值。与谢献忠等[9]研究方案不同的是，李孟珠等[10]设计了1∶30的单跨覆冰输电线路的缩尺模型，开展了链式脱冰和瞬时脱冰的研究，试验结果表明：①与链式脱冰相比，瞬时脱冰跳跃高度更高；②脱冰跳跃最大高度随脱冰速度减小而减小，并最终高度趋于瞬时脱冰的0.5倍；③跳跃最大高度随高差倾角增大而增大。王璋奇等[11]利用了架空输电线路脱冰跳跃试验系统，通过模型试验研究架空非同期脱冰跳跃的动张力特性。其试验结果表明：在脱冰速度相同的情况下，从档中往两端的非同期脱冰方式将在导线中产生较大的张力波动。李孟珠等[10]和王璋奇等[11]都对链式脱冰展开了研究。李孟珠等[10]研究了不同参数和不同脱冰方式下，导线的脱冰振动，其对输电导线的防振设计提供了支撑；王璋奇等[11]则研究的是脱冰对导线的动张力特性的影响规律，在线路设计时应对此充分考虑，防止脱冰产生过大的动张力而破坏架空导线。李宏男等[12]通过悬挂吸附有铁块的电磁铁代替覆冰，建立孤立档冰跳试验，模拟导线覆冰脱落过程，同时利用ANSYS软件计算验证。结果得出导线脱冰跳跃高度与脱冰方向有关：若是从中间向两边脱冰，则跨中跳跃高度最大；若是从两边向中间脱冰，则跨中跳跃高度最小；覆冰脱落前导线的最大静张力和脱落后的最大动张力相差并不大。刘春城等[13]以某地1 000 kV特高压输变电工程为原型，针对脱冰响应进行了模型试验，并建立了有限元模型进行验证，其试验结果确定了输电脱冰动力响应时的最不利工况和最不利位置，为输电塔脱冰跳跃研究提供了依据。

2 数值分析

2.1 输电线脱冰数值方法

由于有限元模拟方法的广泛使用，非线性有限元数值模拟方法已经成了目前学者采用最多的研究方式。该研究方法很大程度上节约了试验经费成本和时间成本。最早利用商业有限元软件进行模拟的是Jamaleddlne等[14-15]，他们利用有限元软件ADINA对导线脱冰进行模拟，并将其所得数据与实验结果进行了比较。文献[16-18]在研究单导线的脱冰动力响应时，也采用了数值模拟的方法，通过此方法得到脱冰位置与覆冰厚度等因素对导线动力响应的影响规律。陈将等[19]利用有限元软件ABAQUS对三挡耐张段线路的脱冰动力响应问题展开了研究，得出脱冰后的导线位移与应力的变化关系和过程。Kollar等[20]也用有限元软件模拟了分裂导线中子导线的脱冰动力响应。李永平等[21]分析了数值模拟方法，构建了1 000 m的大档距架空导线有限元模型，以此分析某一节点导线张力和跳跃高度的变化规律，在线路设计时，对避免导线闪络有一定借鉴意义。侯镭等[22-24]建立了3自由度多档脱冰跳跃模型，对导线脱冰跳跃进行分析，并分析了脱冰量、档距组合等因素对导线脱冰的影响。鲁元兵等[25]用单根导线等效替代分裂导线，再对导线的不均匀脱冰进行了全过程模拟分析，发现脱冰时导线和绝缘子串的张力大幅度增加。鲁元兵等[25]在模拟覆冰的同时，得出一定条件下导线覆冰厚度与导线和绝缘子串所受张力的关系，此研究还对导线和绝缘子串的设计和导线的安全提供参考依据。李春等[26]通过ABAQUS软件建立了导线及耐张串连接金具的模型，以此来研究导线张力对导线连接金具的破坏作用。叶中飞等[27]也利用ABAQUS软件对输电杆塔仿真分析，建立了空间梁杆模型，并通过此方法分析了支撑杆对整体受力和稳定的影响，合理解释了某杆塔的破坏位置。鞠彦忠等[28]在研究导线张力对防振装置的效果影响时，利用ANSYS有限元软件模拟导线-防振器体系的振动，并将数值仿真结果与其进行的模拟实验相对比，两者都能较好地吻合。李嘉祥等[29]研究导线的覆冰脱落振动机理时，也采用了ANSYS软件建立线路模型。此研究结果对于研究线路参数和外部荷载的影响有较重要的实际意义。以上四位学者在研究时，都利用了有限元软件建立模型，从而得可以对不同参数条件下的复杂工况都进行较为精确的模拟。沈国辉等[30]提出了线路脱冰的有限元模拟方法，并对导线“拉链”型脱冰进行了分析，讨论了该类型脱冰对导线动力响应的影响，此研究对工程中“拉链”型脱冰的处理具有一定参考价值。王昕等[31]建立了多跨覆冰输电线路有限元模型，并对导线中跨脱冰和三跨脱冰两种情况进行模拟，研究了线路张拉力、档距等参数对导线脱冰的影响，这些模拟情况所得出的结论对线路安全运行有重要意义。

以上有限元模拟研究内容都是导线脱冰后的动力响应，主要分析了导线所受张拉力、档距等参数对动力响应的影响，并由此得出相关结论。对于输电杆塔与导地线的耦连作用、导线脱冰的脱冰跳跃高度、横向摆幅等方面有待深入研究。

2.2 输电塔线脱冰数值计算结果

对于输电塔线脱冰的数值模拟方法，也已被许多学者采用。尹鹏等[32]针对导线脱冰跳跃问题，以云南至广东某特高压输电工程为实际案例，采用非线性时程分析法和四种双层黏弹铅芯阻尼器布置方案对其进行了控制研究，试验表明黏弹铅芯阻尼器对脱冰导线有良好减震效果。McGlure等[33]利用了有限元软件ADINA对输电线路被破坏后的动力响应进行模拟，虽然其采用的是二维杆塔模型且与实际的差异较大，但其方法对导线脱冰模拟仍具有参考意义。李黎等[34]以非线性有限元方法建立了塔-线耦合模型，分析了某实际工程线路的脱冰动力响应，但其分析重点在于脱冰动力响应，未对多档连续脱冰及塔线体系的安全性进行研究。李雪等[35]按原工程资料建立了输电塔-线体系有限元模型，分析了湖南地区挂靖线220 kV输电线路覆冰倒塔事故的主要原因，考虑水平垂直档距、高差、不均匀覆冰和风荷载对线路的影响，结果表明过载、风载及不均匀覆冰是这次事故发生的主要原因。韩军科等[36-37]也通过实例，分析多种因素，得出输电线路倒塔是由于覆冰过载及纵向不平衡张力过大的原因导致的。杨风利等[38-39]建立ANSYS有限元模型，考虑塔线耦合效应、脱冰位置、覆冰厚度、档距等有关因素，完成了塔线体系脱冰跳跃分析。沈国辉等[40]用有限元数值模拟法建立了四塔五线模型，试验发现，导线覆冰脱落使导线产生低频舞动、绝缘子大幅摆动、部分杆塔出现较大峰值应力。晏致涛等[41]通过有限元理论构建了输电线路塔-线体系的脱冰振动分析模型，并以某实际工程为例进行分析，进行了对跳跃高度、支座反力、水平张力数据变化的分析，进而探讨塔线的多种参数对导线脱冰振动的影响。胡伟等[42]先开展了模拟单根导线覆冰脱落的过程，来比较不同情况下该导线的冰跳规律；再利用数值仿真技术模拟各种工况，其结果与实验结果的差距是在误差允许范围内，从而验证了仿真模拟的正确性；在此基础上，他们建立了3自由度多档导线的模型，分析档数、不同档距组合、档距大小等多种因素对特高压同塔输电线路脱冰跳跃的影响。易文渊[43]利用ABAQUS有限元软件建立了三档四塔精细有限元模型，针对覆冰荷载、风荷载及脱冰荷载因素，数值模拟塔线耦合体系导线的脱冰动力响应；基于该模拟结果，得出了连续档导线最大冰跳高度和横向摆幅的计算公式。程皓月[44]以连续的孤立档覆冰线路为研究对象，建立了有限元模型，分析了500 kV塔线体系在覆冰脱冰工况下的安全性，但因其有限元模型不包含直线杆塔，所以不能代表一般情况。

上述方法主要是围绕500 kV及其以下电压的线路脱冰进行计算。随着特高压输电线路的广泛应用，现有研究研究均缺乏对多分裂、大截面特高压输电导线脱冰跳跃形态及塔线受力特性的研究。

3 脱冰跳跃计算结果

3.1 跳跃动态特性

数值仿真模拟的方法主要是通过有限元软件建立模型，从而分析导线的脱冰跳跃动态特性，这是很多学者常采用的方法，也是近几年很热门的研究方式。有限元模拟中有几种常用方法：附加冰单元法、改变密度法和附加力模拟法。但是研究人员在使用以上方法时，其所取的力学参数并不一致，且未比较各种方法的适用性和等价性[45]。为此，沈国辉等[45]指出有限元分析中的附加冰单元法和改变密度法中冰参数选择的不合理之处，并对有限元模拟的三种方法分别给出了合理建议值。他们认为以往学者将冰的弹性模量取值为10 GPa是不合适的，并根据算例结果给出了不高于0.01 GPa的弹性模量建议取值。杜运兴等[46]用数值模拟方法建立耦合模型，采用附加单元法模拟覆冰，探究了导线两层覆冰不同脱落情况的动力响应，并得出结论：以往的脱冰荷载取值仍有优化空间。邱勇等[47]借助有限元软件建立输变电线路模型，同时再通过改密度法模拟脱冰，分析塔线体系对输电线路的动力响应，其研究结果对防止闪络事故具有指导意义。张宏雁等[48]建立了覆冰破坏的有限元模型，模拟了覆冰导线受冲击荷载作用后的脱冰过程，并得出以下结论：导线脱冰量随荷载冲击增大而增大，当冲击荷载大于一定值时，导线覆冰完全脱落；脱冰效果与荷载作用时间、荷载距导线中点的距离有关。王凌旭等[49]用ANSYS软件建立四塔三线的模型，分析不同工况下，导线脱冰时的受力规律和动力响应，并发现某工况下的导线脱冰振动可导致线路接触闪络。吴天宝等[50]通过有限元模拟的方法，探究了覆冰厚度、脱冰位置、输电线路长度、输电线档数对脱冰跳跃幅值的影响，得出了冰跳高度增加的规律。随着特高压输电线路的广泛应用，部分线路经过高寒地区，目前研究缺乏对特高压线路脱冰的研究。

3.2 跳跃高度

脱冰跳跃高度即是导线脱冰时竖直方向的振动幅度。导线冰跳高度的研究对于导线脱冰动力响应具有重要意义。赵煜哲等[51]采用有限元数值仿真方法，构建出了包含塔、线、绝缘子等的精细有限元模型，针对输电线路的脱冰跳跃现象，分析了多个参数对导线脱冰的影响，并最后得出脱冰跳跃高度的近似计算公式，为实际设计时确定竖向安全距离提供了参考。伍川等[52]基于冰跳过程中的能量关系、应力弧垂关系、变形关系和平衡关系，从而给出了导线最大冰跳高度的计算方法，并利用数值模拟方法和Morgan理论算法验证了该计算方法的正确性。李黎等[53]利用ANSYS及VC++编制互交界面软件来实现有限元分析，并验证了较高精度及实用性；最后在不同参数条件下进行了脱冰工况计算，并提出了冰跳高度简化公式，为线路设计和脱冰振动预防提供了参考依据。谢献忠等[54]基于功能原理和能量守恒定律，推导出了导线跳跃高度的理论计算公式，并利用有限元分析方法进行了验证。前面已有几位学者提出了跳跃高度的计算公式，但对于大档距大高差线路，这些方法并不合适。针对大档距大高差线路，王德千等[55]采用有限元模拟方法来研究脱冰动力响应，分析数值模拟得到的冰跳高度与弧垂差、档距、高差等参数的关系，最后得出冰跳高度的简化公式。该公式同前面已有公式相比，可用于大档距大高差线路，其适用范围更广。伍川等[56]在研究大截面导线脱冰动力响应特征时，利用数值模拟方法确定了 导线最大冰跳高度与导线静止状态下的弧垂差之间存在线性关系，并在此基础上给出了大截面导线的最大冰跳高度简化计算公式，可为工程设计提供指导。白天明等[57]建立三种实验系统、模拟了单导线的7种覆冰脱落工况，从而得到各工况的跳跃位移，并进行了有限元模拟；最后从试验中得出脱冰振动幅值与覆冰厚度呈正相关的结论；该实验对实际脱冰具有指导意义，同时，在此试验中也验证了模拟方法的正确性。文楠等[58]用数值模拟方法获得导线最大冰跳高度，并基于此模拟结果和BP(back propagation)神经网络建立了导线冰跳高度的预测模型；通过与中国规程给出的冰跳高度计算公式比较，其模型预测的计算精度大幅提高，可为覆冰区线路绝缘间隙的设计给出重要参考。

文献[51-56]都通过实验得出跳跃高度的计算公式或简化计算公式。但这些公式受限于多种工况和条件，对于高压、大跨度及受自然条件影响大的输电导线，其实用性有待考究。

3.3 横向摆幅

相比与导线冰跳高度，覆冰导线脱冰时产生的最大横向摆幅的研究并不多，这也可作为导线脱冰动力响应的一个深入研究方向。赵煜哲等[51]在利用有限元数值仿真方法时研究导线跳跃高度时，同时考虑脱冰风荷载作用与横向风荷载的在时间上的相关性，给出了在横向风作用下，导线最大横向摆幅差的计算公式。严波等[59]建立了塔线耦合体系的有限元模型，通过对不同风速、档距、高差、绝缘子串长度等参数条件下的数值结果分析，得出最大横向摆幅与静止状态风偏改变量的定量关系；并由此给出了导线脱冰后最大横向摆幅的简化计算公式，为输电线路绝缘配合设计提供了基础。李黎等[60]在利用有限元模拟研究导线脱冰及风偏问题时，得出了脱冰档最大横向摆幅发生在先风偏再脱冰的情况下的结论；最后研究横摆规律时，提出了横向摆幅的简化公式，为线路和杆塔的设计提供了依据。伍川等[56]采用数值模拟方法，分析各种参数下导线脱冰的动力响应特征，得出横向摆幅的变化规律，并说明了覆冰厚度、脱冰率、档距、档数、风速这些参数对于导线的最大横向摆幅皆有影响，为研究最大横向摆幅计算公式提供了参考。最后根据这些实验结论提出了横向摆幅工程简化计算公式。

以上对导线横向摆幅的研究，是基于不同体系不同条件下得出的计算方法或计算公式。赵煜哲等[51]主要是考虑了横向风荷载和脱冰共同作用的情况，并由此得出了计算导线最大横向摆幅差的公式。与赵煜哲等不同的是，严波等[59]研究耦合塔线体系不同参数下导线的动力响应特征，并由此得出导线最大横向摆幅的工程简化算法；其研究对于线路设计时绝缘间隙值的确定具有重要的实际意义。李黎等[60]是探究了在脉冲风荷载作用下不同参数的横摆规律，从而给出计算导线横向摆幅的简化公式，其对于杆塔和线路的设计有着重要参考价值。伍川等[56]与严波等[59]的研究思路类似，也是在研究了档距、高差等多种参数下导线的动力响应的基础上，获得导线横向摆幅的变化规律；但研究对象是特高压大截面导线，并考虑了温度对脱冰动力响应的影响。

要保证输电线路的安全运行，研究覆冰导线脱冰的动力响应必不可少；而探究导线的动力响应，其冰跳高度和横向摆幅又是动力响应的两个重要表征。导线冰跳高度和横向摆幅对于输电线路动力响应特征及线路杆塔的设计具有重要参考价值，而且目前在此方面的研究较少，需要进行深入研究。

4 结论和展望

总结了中外学者对覆冰导线脱冰动力响应的研究进展，包括各种模拟实验、数值模拟方法、脱冰跳跃计算结果分析等，并得出以下结论。

(1)目前中国研究导线脱冰方法中，利用有限元数值仿真模拟是学者最为广泛采用的方式，适用范围很广，其计算精度和准确度也比较高。

(2)对于导线脱冰跳跃高度的研究，已有研究通过试验给出了跳跃高度的计算方法和简化计算公式，并可适用于多种情况；其中计算精度更高的可为中国规程的改进提供参考。

(3)对于导线横向摆幅的研究，是导线脱冰动力响应研究方向里学者涉及较少的部分；横向摆幅对于输电线路动力响应特征及线路杆塔的设计具有重要参考价值，可在此方向进行深入研究。

(4)随着特高压输电线路的广泛应用，现有研究研究均缺乏对多分裂、大截面特高压输电导线脱冰跳跃形态及塔线受力特性的研究。

(5)在前期的研究基础上，可以综合利用多学科交叉，提出脱冰跳跃预测技术与智能除冰系统研究。