浅表走滑构造系统砂箱物理模拟研究进展

谢玉洪

浅表走滑构造系统砂箱物理模拟研究进展

谢玉洪

(中国海洋石油集团有限公司, 北京 100010)

地壳浅表走滑构造系统发育于多种类型的地球动力学背景, 不仅具有较强地震危害性、也富集油气矿产等资源。自20世纪初以来, 基于地质构造过程自相似性和“无理有效性”的砂箱物理模型为走滑构造系统演化特征与机制等研究提供了独立有效的手段。自然界走滑构造系统动力学上可分为板缘构造转换断层和板内走滑断层体制, 空间几何学上可分为走滑断层弯曲类和走滑断层叠置类。基于吕德尔剪切和弥散性剪切砂箱物理模型实验共同揭示出, 走滑剪切系统主走滑变形位移带发育五类断裂/破裂体系, 即R型破裂、R′型破裂、P型剪切、张破裂和Y型破裂, 尤其是在弥散性剪切变形过程中发育大量的RL和RL′型斜切剪破裂。浅表走滑剪切构造系统分段性及其走滑转换带差异变形特征受控于基底走滑断层应力‒应变条件沿走向差异变化的特性, 基底断层几何学(弯曲/叠置性、间隔性等)、砂箱动力学特性(纯走滑剪切、拉分走滑和挤压走滑剪切)、非均质性砂箱物质特征(黏土和膏岩等)、基底非均一性(塑性基底物质几何学等)等对走滑构造变形过程具有明显的控制作用。砂箱物理模拟实验能为走滑构造系统运动学、变形特征与机制等提供较好的解释模型, 能有效再现走滑构造形成演化的四维过程与机制, 在地震灾害机理、油气勘探等方面将发挥越来越重要的作用。

砂箱物理模型; 走滑变形; 吕德尔剪切; 弥散性剪切

0 引 言

走滑构造系统普遍发育于不同类型的地球动力学背景, 如: 板缘环境(新西兰Alpine断层带、美国San Andreas断层带和Dead Sea断层带等)、板内环境(阿尔金断裂带、郯庐断裂带和鲜水河‒小江断裂带等, 图1)等。走滑构造系统由动力学成因上相互联系的、次平行‒平行的走滑断层体系所组成, 断裂体系空间上普遍具有非线状或弧形特征、宽度可达数百公里(图1), 走滑断裂带发育复杂的拉张和/或挤压构造变形, 它们通常与走滑构造带主断层及其两侧块体运动矢量密切相关(Sylvester, 1988; Mann, 2007)。走滑构造变形系统是重要的地震活动带, 如: San Andreas走滑断层带其地震活动带宽大500 km、鲜水河‒小江走滑断层的地震活动宽度达200 km, 因而具有严重的地震危险性。同时, 走滑构造变形系统通常形成具有不同构造热体制、沉积建造特征的沉积盆地, 从而具有不同的油气矿产富集性(图1), 如: 莺歌海‒琼东南盆地(天然气资源量达1.5×1012m3)、渤海湾盆地(石油探明储量达140.52×108t)(国土资源部信息中心, 2014)等。

地质过程的自相似性(Self-similarity)和砂箱构造物理模型相互验证等揭示出实验模型与自然界原型等具有一定的相似性(无理的有效性“Unreasonable effectiveness”, Wigner(1960), 即不同尺度上几何学‒运动学‒动力学过程的相似性(Hubbert, 1937)), 构成砂箱物理模拟实验理论基础。自Cloos(1928)和Riedel(1929)开创性使用平直基底活动板片与上覆石英砂模拟走滑构造变形过程以来, 近百年走滑构造系统砂箱物理模拟实验装置和理论体系产生了极大的革新变化(Koyi, 1997; Dooley and Schreures, 2012)。从防震减灾人居环境、到油气矿产资源勘探预测等不同方面, 以自然界原型和实验模型对比研究(“From nature to models”)为科学思想的砂箱物理模拟手段受到了的广泛重视和应用(Dooley et al., 1999; McClay and Bonora, 2001; Wu et al., 2009; Leever et al., 2011; Zuza et al., 2017), 如: Zuza et al. (2017)基于砂箱物理模型和地震活动研究揭示出活动走滑断裂系统的活动强度与浅部脆性地壳厚度和力学条件等密切相关(图1b); 任健等(2017)和陈兴鹏等(2019)分别通过砂箱物理模拟和渤海湾走滑构造系统研究揭示辽东湾地区典型拉张走滑变形过程的含油气构造样式等。

(a) 中国及邻区主要陆内走滑断裂体系, 其中红色圆圈示青藏高原地区6级以上地震(据曾融生和孙为国, 1992; 邓起东等, 2014); (b) 走滑剪切带深度(即地震活动深度)与弥散性断层带间距(Zuza et al., 2017)。

因此, 本文主要基于自然走滑构造系统为研究对象的砂箱物理模拟研究结果, 系统阐述地壳浅表走滑构造系统“实验模型‒自然原型”间相似性机理, 揭示砂箱物理模拟实验能够有效再现走滑构造形成演化的四维过程特征与机制, 从而为走滑构造系统运动学、变形特征与机制等提供较好的解释模型, 并以维也纳盆地低角度拉分走滑盆地和青藏高原东缘红河弧形走滑构造实例对比为典型案例, 以期为研究同行提供参考与借鉴。

1 走滑构造系统形成过程机制与特征

瑞士地质学家Arnold Escher von der Linth基于近8 km的地表线状构造(即“the Sax Schwendi fault”)及其发育的水平擦痕和阶步特征, 在19世纪50年代最早记录和解释了左旋走滑断层活动、其断距约500～800 m(Sylvester, 1988)。1906年旧金山地震导致San Andreas断层活动形成最大达4.7 m右旋走滑活动, 断层走滑活动作用及其意义逐步开始受到地质学界的广泛关注。“走滑断层, Strike-slip fault”强调断层动力学含义, 主要指断层具有平行于其走向的运动矢量(Reid et al., 1929)。随后, 扭断层“wrench fault”、转换断层“transform fault”和横断层“transcurrent fault”等概念也广泛应用于走滑断层阐述。Woodcock (1986)和Sylvester (1988)将其主要归为两类走滑断层系统即: 板缘构造转换断层“Interplate transform fault”和板内走滑断层“Intraplate transcurrent fault” (图2)。前者主要位于板块边界的、切割岩石圈的区域性走滑断层系统, 如: 洋中脊转换断层、海沟机制走滑断层等; 后者主要为不同类型的、较小断层发育深度(局限于岩石圈内部)的走滑断层系统, 如: 构造结机制走滑断层、撕裂断层等。因此, 走滑构造系统具有多种成因机制, 包括: (1)不规则板块/块体碰撞, (2)力学属性条件侧向变化导致的岩石圈变形, (3)相邻板块/块体不均一运动, (4)板块/块体差异性旋转或碰撞等机制(Storti et al., 2003; Mann, 2007)。

由于自然界沿走滑构造变形带中地层通常具非均质性特征, 导致其带内主断裂和次级断裂连接、生长形成不规则的走滑断裂带/系统(Sylvester, 1988; Storti et al., 2003; Mann, 2007), 其走滑断裂系统不规则性可以大致分为两类: 走滑断层弯曲类“Bends”、走滑断层叠置类“Stepovers, jogs or offests”(Sylvester, 1988; Woodcock and Schubert, 1994)。前者为走滑断层走向相连、但发生弯曲, 否则为断层沿走向发生断离、不连续(图2)。陈发景等(2011)基于渤海湾盆地走滑拉张构造特征出发, 进一步归纳为: (聚敛型和背离型)共轭反向类和同向类走滑转换带/调节带。需要指出的是, 浅表发育的走滑断层叠置带通常伴随深度增加逐渐转化为走滑断层弯曲带, 即浅表相互断离的走滑断层在深部逐渐连接形成弯曲的走滑断层。基于我国东部地区独特复杂的板内走滑动力学过程, 我国地质学家进一步完善和发展了走滑断裂体系中走滑派生构造或走滑转换带(漆家福, 2007; 陈发景等, 2011; 童亨茂等, 2013; 黄雷等, 2019), 徐长贵(2016)系统总结归纳渤海海域存在(基于空间位置结构分类的)断边转换带、断间转换带和断梢转换带三大类型, 和(基于局部应力状态分类的)增压型和释压性走滑转换带两小类走滑转换带, 尤其是增压型转换带石油地质储量占郯庐断裂带81%总地质储量。吴智平等(2016)强调走滑与拉伸构造叠加导致走滑主断裂走滑侧接作用形成走滑双重构造, 其平面空间上具叠瓦状、剖面空间上具典型花状结构, 也可以基于应力‒应变特征分为挤压和拉张型走滑双重构造类型。由于断块层系相对于主走滑变形位移带(即The principal displacement zone (PDZ))不同运动矢量特征, 导致发育复杂的拉张和/或缩短构造变形过程, 逐渐形成汇聚型(即“Transpressional, 或Restraining”)、和离散型(即“Transtensional, 或Releasing”)走滑构造变形带, 从而形成汇聚挤压变形的隆起构造和离散拉张变形的拉分盆地, 它们垂直剖面切片上具有典型的正花状或负花状构造特征(图2b)。基于我国东部郯‒庐断裂带渤海湾地区复杂走滑构造特征研究, Huang et al. (2017)揭示张扭带内走滑相关挤压变形作用形成的“特殊花状构造”, 即正断层和背形组合构造样式(图2b), 而明显区别于典型的正花状或负花状构造样式(图2b)。

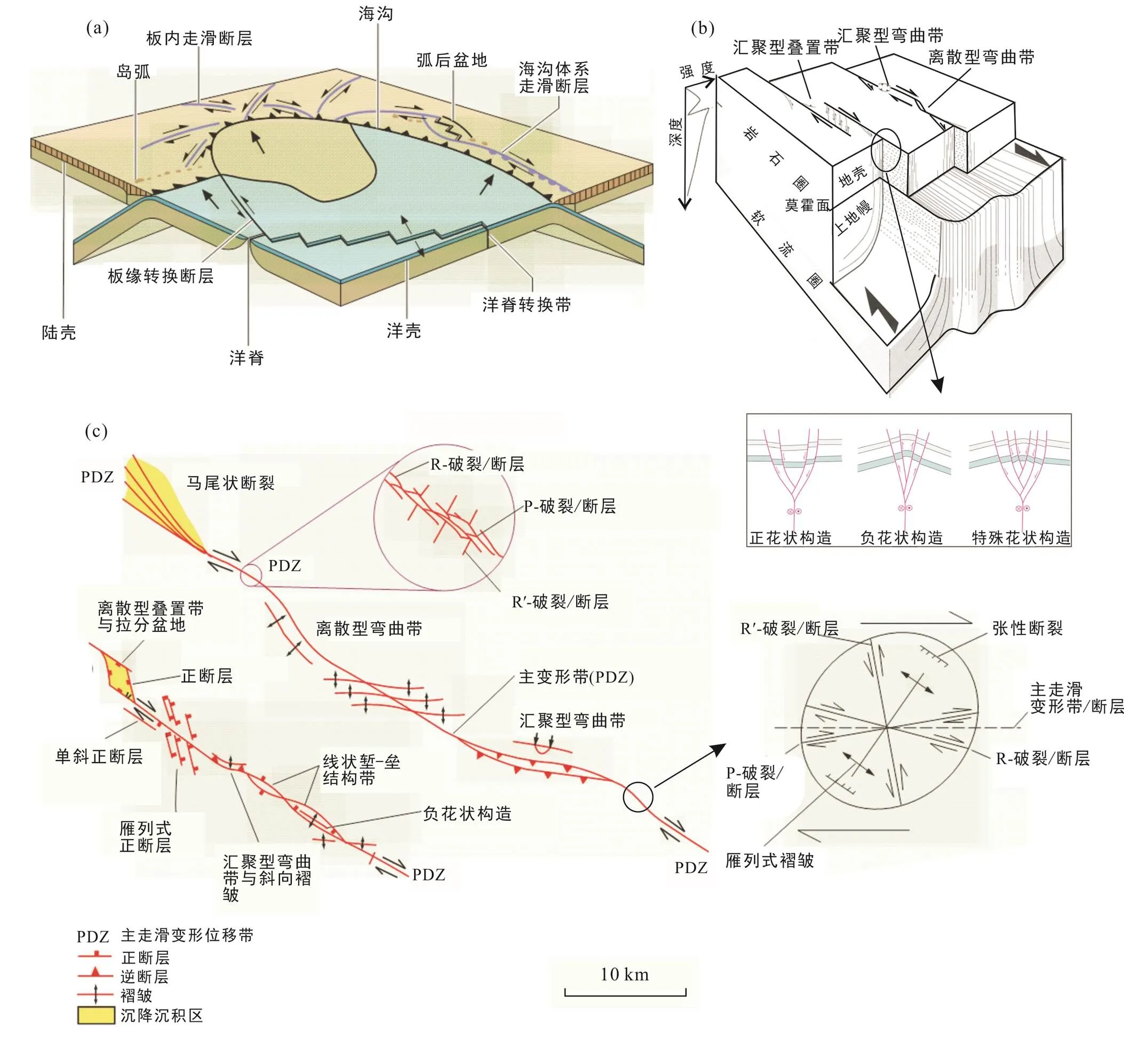
(a) 走滑构造系统的板块动力学机制及其板内和边缘走滑构造体系特征(Woodcock, 1986); (b) 板内走滑构造系统模式图与典型走滑断裂系统类型, 示伴随走滑剪切变形深度增加其走滑断裂带倾角和厚度持续变化特征(Storti et al., 2003), 其中插图示三类典型走滑花状构造样式: 负花状结构、正花状结构和特殊花状结构(正断层和背形组合构造样式)(Huang et al., 2017); (c) 右旋走滑构造系统典型构造特征综合图, 揭示右旋走滑构造主走滑变形位移带(PDZ)分段性与典型构造特征综合图、应力‒应变机制与伴生五类断裂特征图(Wilcox et al., 1973; Bartlett et al., 1981)。

2 砂箱物理模型与走滑构造“实验‒实例”互证分析

2.1 走滑构造砂箱物理模拟实验装置

基于板内和板缘普遍存在的线性走滑剪切变形带特征(图2a), Cloos(1928)初次进行走滑构造砂箱物理模拟实验(图3a), 即广为熟知的吕德尔剪切实验(“Riedel experiment”, Tchalenko, 1970), 其模型设备装置为两部分组成: (1)基于产状近直立的、平直的基底断层(由两块相邻刚性基底组成, 其中一块固定、另一块发生水平运动位移), (2)基底断层上覆未变形地层系统。吕德尔剪切物理模拟实验揭示基底断层上覆未变形物质的纯剪切走滑构造变形特征, 此后该模型实验装置得到广泛的改进与完善, 如: 转换挤压和转换拉张剪切物理模型(Naylor et al., 1986; Richard and Cobbold, 1990)和多走滑基底断层剪切物理模型(Richard et al., 1995; Schellart and Nieuwland, 2003)等。

20世纪50‒70年代, 不同的黏土材料、玻璃珠和石英砂等物质被广泛应用于吕德尔剪切实验模拟过程中, 揭示物质属性对走滑剪切变形过程的影响性(Cloos, 1955; Tcalenko, 1970; Wilcox et al., 1973; Harding, 1974)。伴随旋剪试验和环剪试验手段进步, 揭示出干颗粒材料(即石英砂、玻璃珠)、湿黏土材料普遍遵循Mohr-Coulomb破裂准则(Davies et al., 1983; Lohrmann et al., 2003; Withjack et al., 2007), 具有与上地壳岩石变形相似的流变学机制(Marone, 1998; Panien et al., 2006; Klinkmuller, 2012)。湿黏土材料通常具(较高)粘聚强度和含水性、且粘聚强度伴随密度增大而增大(可能主要受含水性控制)(Arch et al., 1988; Eisenstadt and Sims, 2005)等缺点, 但其对走滑构造相关裂缝发育特征具有更好的显示性(Eisenstadt and Sims, 2005; Withjack et al., 2007)。

20世纪中‒晚期以来, 地质学家们普遍认识到自然界走滑剪切变形过程并不局限于某一狭窄构造带, 而常常分布于数十至数百公里宽的构造带(图1b), 从而形成弥散性剪切变形带(“Distributed strike-slip”),如: San Andreas断裂系统、新西兰Alpine断裂系统和Dead Sea断裂系统等, 因而弥散性走滑剪切砂箱构造物理模拟实验也广受关注(Naylor et al., 1986; Richard et al., 1995; Schreurs, 2003)。弥散性剪切带变形物理模型主要由两块相互独立的基底板片与上覆平行排列的细板片(即5 mm宽有机玻璃棒, 图3c)装置组成, 它们分别发生水平剪切位移导致上覆砂箱物质由长方形(或正方形等)发生弥散性剪切逐渐转变为平行四边形。同时, 由于自然界变形过程中普遍具有多期叠加变形过程(即拉张走滑或挤压构造变形等), 因此走滑变形过程与挤压缩短、或拉张变形叠加过程也受到较广关注(Naylor et al., 1986; Sylvester, 1988; Richard et al., 1990; An and Sammis, 1996), 它们主要基于基底板片的叠加过程来实现自然原型实例的物理模拟(图3e-f), 通过基底板片之间不同夹角来模拟走滑拉张构造变形、纯走滑剪切变形和不同动力学变形过程的叠加构造变形过程(Sota, 2006; Rosas et al., 2012)。需要指出的是, 通过对基底断层的弯曲或相互叠置条件设置, 实现对不规则性走滑断裂系统(即走滑断层弯曲类和叠置类、或者走滑转换构造带等)构造变形过程模拟(图3d)。由于复杂大陆动力学背景导致我国东部地区普遍具多期走滑或拉张叠加构造特征, 因此更加侧重于对于先存构造或基底、多期走滑与拉张复合作用过程的物理模型实验装置(朱战军和周建勋, 2004; Tong et al., 2014; 李艳友等, 2017), 同时也暴露出简化物理模型装置与复杂地球动力学之间与生俱来的矛盾(图3)。

无论吕德尔和弥散性剪切实验模拟装置都普遍强调基底主边界断层在地壳变形过程中的重要性, 但自然界变形过程中地层力学机制条件, 如: 空间几何学、能干层、流变学和非均一性等, 流体水‒岩反应和流体超压作用等在地壳变形过程中都具有至关重要作用, 但受限于实验装置设计条件, 它们普遍未能够在实验模拟条件下实现。尤其伴随多期构造变形过程中, 地壳浅表变形作用普遍具有复杂动力学过程, 如: 多期走滑反转、多期旋转动力拉张走滑构造过程、稳态和非稳态浅表剥蚀‒沉积作用等, 它们如何在简化走滑砂箱模拟装置中实验实现是有待解决的难点之一(如: Sun et al., 2003; Yu and Koyi, 2016; 邓宾等, 2016, 2018; 陈兴鹏等, 2019), 如: 郯‒庐断裂带渤海湾盆地早期左旋走滑和晚期右旋走滑反转叠加(漆家福等, 1994; 张婧等, 2017)、青藏高原东缘红河走滑带早期右旋走滑和晚期左旋走滑反转叠加, 南海珠江口盆地新生代多期(顺时针旋转)拉张走滑动力学变形叠加过程(Ye et al., 2018)等。

新世纪以来, 深部岩石圈过程、浅表作用过程(如: 同构造沉积、构造剥蚀等)和浅表(走滑)构造变形之间的相互作用受到越来广泛的关注, 因而浅表构造作用过程普遍被作为典型走滑变形条件被应用于砂箱物理模拟实验中(Guerroue and Cobbold, 2006; Paola et al., 2009)。伴随计算机和数值CCD相机进步, 能更加高分辨率地获取砂箱模型中不同像素或点阵运动规律。粒子成像测速技术(PIV, Particle Imaging Velocimetry)是基于两个连续时间切片中应变标志体(如石英砂颗粒等)运动, 有效量化砂箱模型运动学。每个时间切片的照片被划分为不同的审讯窗口(Interrogation windows, IW), 下一个连续时间切片上的相同位置的审讯窗口颗粒位置取决于其增量运动或增量应变(时间间隔内分别沿X轴和Y轴), 通过计算这两个审讯窗口可以得到该处的运动矢量(V)(Hoth, 2005; Adam et al., 2005)。它们的绝对空间分辨率和位移矢量精度取决于审讯窗口大小、CCD成像精度和相关算法, 总体上都能够达到数0～0.5 cm精度。尤其是激光扫描技术、三维立体CCD技术和激光干涉仪等设备在砂箱物理模型中的使用, 使砂箱模型实验的空间分辨率达到小于1 mm的精度(Graveleau et al., 2008; Schrank and Cruden, 2010)。早期砂箱物理模拟实验受限于如何有效对砂箱内部变形特征进行检测, 但(螺旋)X射线计算机层系成像技术、CT扫描技术和地震反射技术等的应用, 使我们能够在不破坏砂箱模型条件下(任意时间切片和任意空间方向上)连续检测和获取砂箱模型内部变形运动学过程(Colletta et al., 1991; Schreurs et al., 2003; Adam et al., 2013)。近5～10年 4D X射线层系成像和DIC(Digital Image Correlation)粒子耦合数字图像系统的发展, 初步实现了全时域三维监测和(量化)揭示砂箱物理模拟实验过程中外部和内部变形特征(Colletta et al., 1991; Adam et al., 2013; Zwaan et al., 2018)。

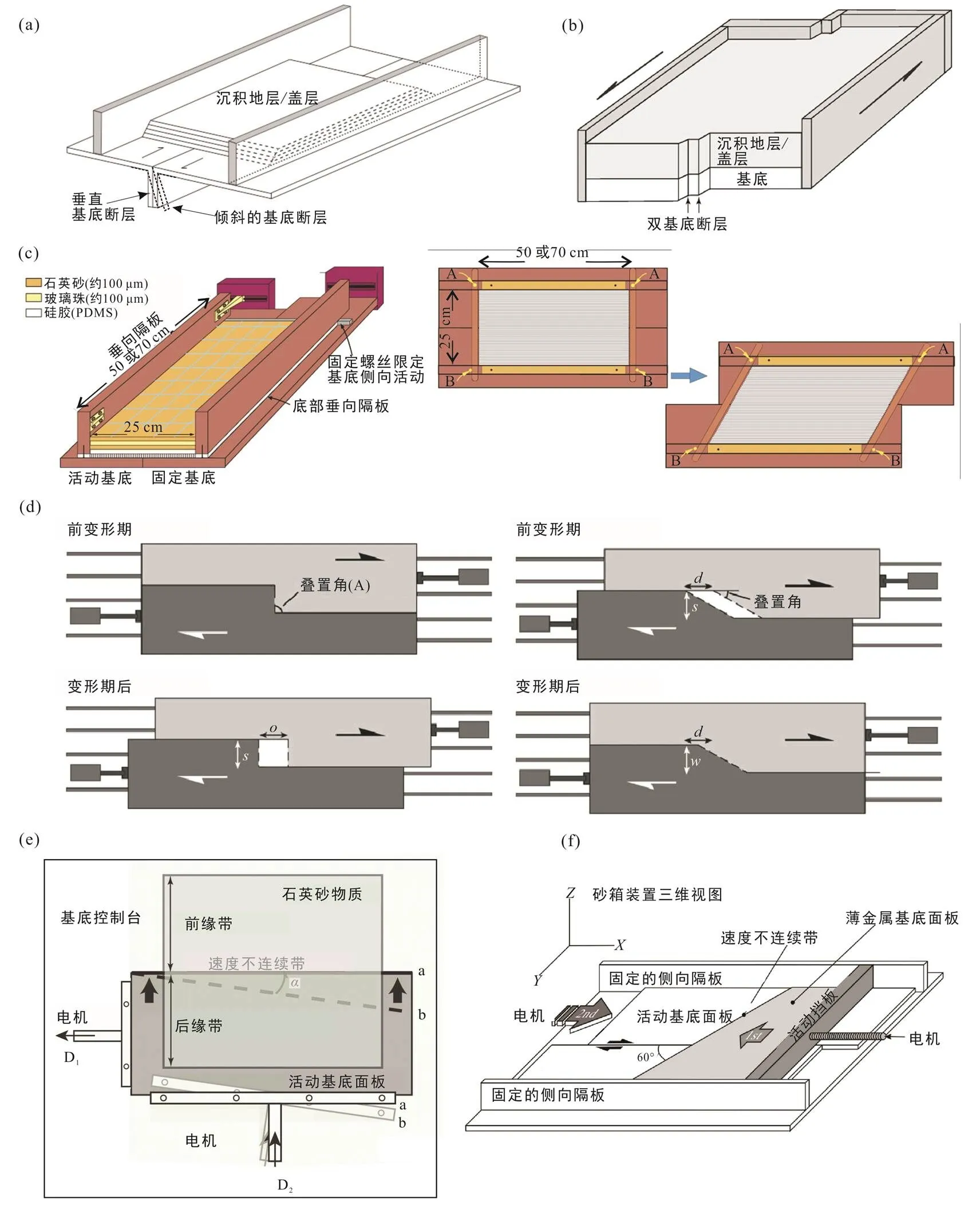
(a) 吕德尔剪切砂箱物理模型装置, 砂箱基底主断层具有垂直或倾斜等不同边界条件, 若垂直代表为典型吕德尔砂箱模型边界条件(Dooley and Schreures, 2012); (b) 多走滑基底断层剪切物理模型装置(Schellart and Nieuwland, 2003), 上覆砂箱物质变形特征受下覆两条垂直平行基底断层控制; (c) 弥散性剪切砂箱物理模型实验装置及其剪切变形示意图(Schreurs, 2003; Dooley and Schreures, 2012), 其中字母S、O分别表示主断层间距和叠置程度; (d) 走滑剪切带基底断层叠置或弯曲类砂箱物理模型装置(Dooley et al., 1999; McClay and Bonora, 2001); (e, f) 多期叠加走滑挤压变形砂箱物理模型装置, 可以通过进一步控制D1期走滑变形模型中基底活动板片与固定板片夹角来模拟走滑拉张变形过程(即a>0)或纯剪切走滑变形过程(即a=0)(Soto et al., 2006); 同时后期叠加挤压过程中通过控制基底活动板片速度不连续界限(Velocity discontinuity, VD)与早期走滑剪切主断层夹角, 来揭示斜向挤压叠加变形作用过程(Rosas et al., 2012)。

21世纪以来, 尤其伴随计算机运算模拟能力的进步使地壳物质变形过程能够被连续本体/介质、离散颗粒等计算机数值算法模拟, 数值模拟算法可大致归纳为两类: 连续介质算法(包括有限元法“finite element method”、有限差分法“finite difference method”和边界元法“boundary element technique”等)和颗粒动力学算法(包括离散元法“discrete element method”、接触动力学法“contact dynamics method”和晶格/颗粒流法“lattice-solid method”等)。一般而言, 连续介质算法强调通过不同本构关系/模型(Constitutive laws)来模拟地壳差异性物质条件, 而颗粒动力学算法则强调物质变形本身的应力‒应变行为机制(Li and Liu, 2004; Munjiza, 2004; Gray et al., 2014), 数值和物理模拟手段相辅相存、能够为自然界走滑断裂体系原型模拟及其构造特征研究等提供有效手段。

2.2 吕德尔剪切物理模型

早期吕德尔剪切物理模型实验普遍以均质性物质为主(如: 石英砂或黏土), 揭示走滑剪切构造变形过程的差异性(Tchalenko, 1970; Naylor et al., 1986)。典型黏土物质砂箱物理模拟实验中, 早期雁列式、正向吕德尔剪切破裂(即R剪切, 即“Synthetic shear”)走向与基底主断层夹角约12°(=12°), 伴随走滑位移量增加R剪切走向传播旋转、导致其走向与基底断层夹角减小或近平行(图4a)。随后, 进一步形成与基底主断层呈低角度夹角的正向剪切破裂(即P剪切, 即“Secondary synthetic shear”), 其与基底断层反向夹角约10°(=−10°); 伴随走滑位移量增加P剪切与R剪切相交形成呈菱形的正向位移变形带, 即Y剪切(Morgenstern and Tchalenko, 1967)。在较低含水量黏土砂箱模型中, 常常发育反向的吕德尔剪切破裂(R′剪切, 即“antithetic shear”), 它常与早期R剪切呈近80°夹角。R剪切和R′剪切相互共轭、它们夹角平分线分别平行于最大和最小主应力方向。均质石英砂构造物理模拟实验中, 早期雁列式、正向R剪切破裂=17°～20°, R剪切破裂伴随走滑位移量增加形成分支或扩散破裂(图4b), 随后R剪切破裂末端形成低角度正向剪切破裂、其夹角普遍小于17°, 且P剪切破裂形成、常具较低角度夹角特征(Naylor et al., 1986)。与黏土物质砂箱模型中剪切走滑变形同时形成R剪切和R′剪切相反, 石英砂模拟实验中R′剪切普遍形成于晚期, 且剪切破裂位移普遍大于黏土物质中剪切走滑破裂变形位移量。自然界实例和砂箱物理模拟实验中R剪切和高角度共轭R′剪切发育程度具有明显的主次性, 其成因可能归结于砂箱物质粒间孔发育程度、非线性应力‒应变物质特征、物质非均一性等(Schmocker et al., 2003; Katz et al., 2006; Misra et al., 2009), 尤其是砂箱物质中片状矿物的增加所导致的物质非均一性(图4e), 将会显著增加(与剪切带呈低角度夹角)R剪切破裂变形的集中发育程度(Misra et al., 2009; Cooke et al., 2013)。

一般而言, 较高的剪切变形强度普遍导致更宽的走滑剪切带、较发育的R′剪切(而R剪切较少), 但砂箱物质厚度增加通常也会导致R剪切破裂较少(Atmaoui et al., 2006); 砂箱物质浅部的雁列式破裂变形普遍向下逐渐归并入深部基底走滑断层、与自然界走滑剪切带逐渐归并于主剪切断层切割岩石圈深部特征相一致(图2b), 且相邻或叠置的走滑断裂间形成典型走滑隆起带(Naylor et al., 1986; Richard et al., 1995; Ueta et al., 2000), 剪切带宽度普遍与砂箱物质厚度及其内摩擦角相关(Le Guerroue and Cobbold, 2006)。不同走滑剪切动力学特性对砂箱物理模拟构造变形具有明显不同的控制作用(Naylor et al., 1986; Richard and Cobbold, 1990; Richard et al., 1995; Schellart and Nieuwland, 2003; Tong et al.,2014), 如: 走滑拉张、走滑挤压和倾斜基底断层等。倾斜的基底主断层物理模拟(挤压)走滑剪切构造变形过程中, 砂箱上盘常形成雁列式非对称性断层, 断层临近基底主断裂普遍具有较高的走滑分量、远离基底主断裂则具有较高逆冲分量; 而(拉张)走滑剪切构造变形过程中, 砂箱物质普遍具有较对称性破裂变形特征(图4d), 断层几何学特征与基底主断层位移量和上覆砂箱物质厚度之比密切相关(Richard et al., 1995)。当砂箱物理模型具有多条基底断层时, 砂箱物质断层发育特征主要受控于基底断层间隔与上覆砂箱物质厚度之比(Richard et al., 1995; Schellart and Nieuwland, 2003)。当其比率较低时(0.25～0.5)砂箱物质早期形成叠置的、较长的R剪切破裂带(图4e), 伴随走滑剪切位移增大低角度R剪切、R′剪切和P剪切逐渐形成相互叠置的破裂变形带; 当比率较大时砂箱物质形成两个相互独立的走滑剪切变形带。

5)支架被搬运到掘进工作面合适位置后，顶梁油缸、护帮油缸加压，油缸伸出，伸缩梁伸出，直至护帮板与两帮接触，完成支架的伸展动作，立柱油缸、护帮油缸加压，支架立柱升起，直至顶梁与顶板接触，完成支架的升架动作，支架支撑后在两帮位置打锚杆。

(a) 黏土物质砂箱物理模型剪切破裂发育过程及其特征 (Tchalenko, 1970); (b) 石英砂物理模型剪切破裂发育过程及其特征(Naylor et al., 1986), 相对于黏土物质模型其剪切破裂具有较高的初始R剪切破裂角; (c) 具45°倾角基底主断层砂箱物理模型剪切破裂与断裂等发育特征 (Richard et al., 1995), 其中SS/DS为走向滑动与倾向滑动比率, 注意挤压走滑变形与拉张走滑变形构造样式的差异性; (d) 双垂直基底主断层砂箱物理模型剪切走滑变形过程及其特征(Richard et al., 1995), 其中S/T为基底断层间隔与上覆砂箱物质厚度之比; (e) 物质非均一性(Sand: Talc, 即石英砂: 滑石)对R剪切和R′剪切集中发育程度影响(Misra et al., 2009)。

2.3 弥散性剪切带变形物理模型

弥散性走滑剪切砂箱物理模拟变形过程中早期走滑剪切破裂变形具有长演化周期、且控制着后期构造变形过程(Gapais et al., 1991; An and Sammis, 1996; An, 1998; Schreurs, 2003), 它通常形成两类不同剪切变形破裂或断裂(Schreurs, 2003), 一组为共轭R剪切和R′剪切、另一组为晚期应力场旋转形成的斜切破裂/断裂(RL或RL′), 主要发育于R剪切和R′剪切间(图5a)。伴随剪切应变量增加, 相邻断裂间常形成平行于剪切带走向的隆起带, 尤其是R剪切(或R′剪切)的“合并联合”现象, 即相邻剪切断裂沿走向传播、叠置与合并演化, 或者R剪切断裂(或R′剪切)之间的较短的、正向和反向剪切断裂的形成, 这些剪切断裂与R剪切(或R′剪切)断裂具有较低的夹角(RL或RL′)。

虽然砂箱物质弥散性剪切变形过程中早期变形阶段R剪切和R′剪切都普遍发育, 但由于砂箱模型边界条件的差异(如: 几何类型或砂箱物质成分等), 可能导致剪切变形过程中砂箱物质以R′剪切变形为主的(Gapais et al., 1991)。不同方向的斜向挤压剪切动力学条件对砂箱物质变形过程也具有重要的控制和影响作用(Schreurs and Colletta, 1998), 如: 斜向挤压汇聚角(挤压方向与走滑剪切边界夹角)较低时, 砂箱物质早期主要形成走滑剪切破裂变形, 但其角度超过18°时逐步形成走滑逆冲破裂变形(图5b)。弥散性剪切变形过程中砂箱物质能够发生侧向位移(砂箱横向边界即“transverse boundaries”不固定, 图5c), 这与我国东部渤海湾地区发育的凹陷边界断层“跃迁”特征具有相似性(童亨茂等, 2018); 晚期RL或RL′剪切破裂伴随剪切应变增加形成具弱倾向滑动的“S”型或“Z”型弯曲变形, 同时形成旋转构造和张性堑‒垒结构等(图5c), 它们与拉张走滑体系下大量弧型弯曲走滑断裂带特征相一致, 如: 渤海湾辽西构造带(徐长贵, 2016; 柳屿博等, 2018)。

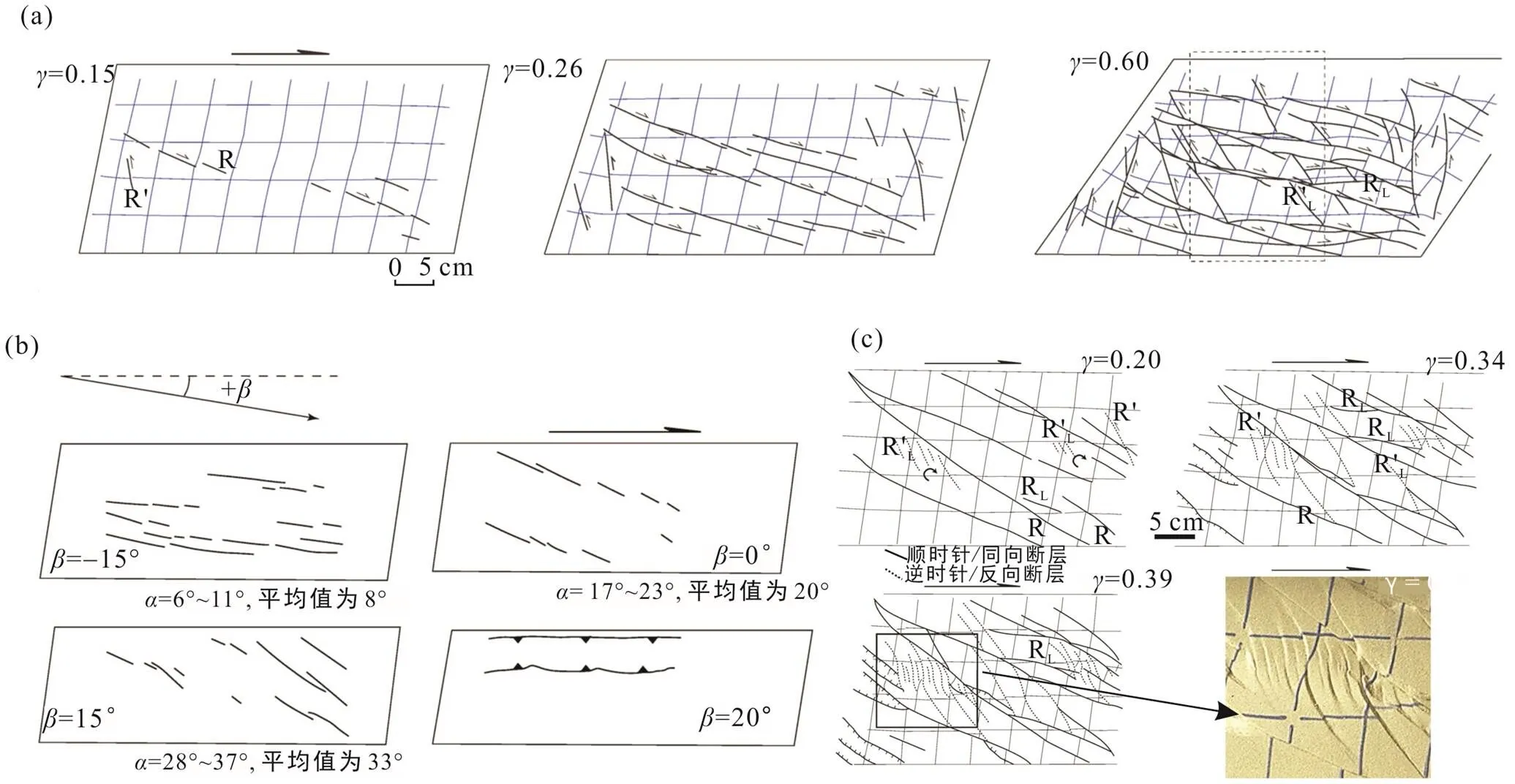
(a) 弥散性剪切砂箱物质走滑剪切变形过程及其特征(Schreurs, 2003); (b) 斜向弥散性剪切变形过程砂箱物质表面断裂发育特征对比图 (Schreurs and Colletta, 1998), 其中β为主应力方向与基底断裂或剪切主边界夹角, 负值为张性剪切、正值为挤压剪切, β=0为典型弥散性剪切变形模式; (c) 横向或侧向边界不固定条件下弥散性剪切砂箱物质变形过程(Schreurs, 2003), 其主走滑剪切断裂间形成旋转变形和张性堑垒结构。

吕德尔剪切砂箱物理模拟实验中主剪切应变带走向平行于基底主断裂, 伴随剪切变形增大该主剪切应变带变窄、形成典型的主走滑变形位移带(PDZ) (Naylor et al., 1986; Richard et al., 1995); 弥散性剪切物理模拟实验中复合的正向剪切带一般与砂箱模型基底主断裂具有10°～15°夹角, 伴随剪切变形增大该主剪切应变带变宽。由于吕德尔剪切物理模型实验中基底主断裂走向大致平行于潜在的低角度RL剪切破裂走向, 其不发育低角度RL剪切破裂变形, 因此R剪切破裂叠置合并常常形成Y型剪切; 相反在弥散性剪切变形模型中, 发育大量的RL和RL′剪切破裂变形。一般而言, 自然界中弥散性剪切带变形模型普遍具有如下特征(Schreurs, 2003): 数条分散的、叠置的主走滑断裂, 主走滑断裂间普遍发育年轻的、较短的和具(相对于主走滑断裂)较小走滑变形的走滑断裂(其剪切属性与主走滑断裂相反), 主走滑断裂和(直线型或弯曲的)RL或RL′剪切断裂间常发生物质旋转变形形成隆起带或凹陷带。吕德尔剪切和弥散性走滑剪切物理模拟实验中都普遍揭示出物质剖面结构上花状结构样式, 它们与自然界走滑断裂体系具一致性, 尤其是弥散性走滑剪切物理模拟实验中所揭示的大量物质旋转、断层侧向斜列叠置和传播生长等与自然界复杂走滑变形特征体现出较好的相似性(图2、图5)。

2.4 走滑剪切构造变形分段性及其主控因素

自然界中走滑剪切构造带普遍由连续的、具分段性断裂体系及其走滑转换带构成, 如: 断层带弯曲/叠置带(包括低叠置/过叠置(即“Underlapping or Overlappingt”)、断层间隔性(即“stepover distance/ width”))等。基底断层走向变化、叠置等几何学特征变化常常导致走滑剪切构造系统中应力‒应变条件沿走向差异变化, 它是走滑断裂分段及走滑转换带构造变形差异的重要控制因素之一(Dooley et al., 1994; Richard et al., 1995; McClay and Bonora, 2001; Mann, 2007; 马宝军等, 2009; Mitra and Paul, 2011)。弧形弯曲基底走滑主断层砂箱物理模拟揭示, 受控于弧形主走滑断层主应力场与基底断裂夹角沿两侧的差异性(即弧形主走滑断裂两侧明显不同走滑挤压剪切应力分量), 导致砂箱物质应变差异、相关断裂具不同发育序列和发育程度(Dufrechou et al., 2011)。一般而言, 弧形主走滑断层内凹侧较早形成吕德尔剪切断裂、且具有较高发育程度, 随后主断层凸出外侧形成较稀疏R断裂, 最终形成平行于主走滑断裂的弧形断裂体系(图6c)。基于走滑断裂叠置长度、横向间隔和走滑位移量等, 任健等(2017)揭示走滑构造带系统中走滑断层叠置长度增加和横向间隔距离减小都会导致走滑转换带内横向断层与斜向断层数量比增加, 且它们之间存在一定的比例函数关系。复杂拉张走滑构造变形作用下, 伸展与走滑作用的强弱配比关系控制影响着断裂发育特征(陈兴鹏等, 2019), 走滑作用与伸展拉张作用复合联合形成平面上具帚状或梳状组合断裂样式、发育R和P剪切断层等, 垂向剖面成多级“Y”字形、似花状构造或负花状断裂组合样式等(图6b)。走滑剪切带断层走向末端, 由于应力‒应变逐渐沿走向释放撒开、导致平面上呈马尾状断裂组合样式(即帚状断裂体系), 且伴随地层能干性减弱或软弱层厚度增加, 帚状断裂体系平面延伸长度和宽度显著增大、走向稳定性增强, 从而形成系列规模较大的断块, 而区别于走滑剪切转换带构造变形特征(McClay and Bonora, 2001; 李艳友等, 2017)。

一般而言, 压扭性断层弯曲或叠置带、走滑转换带等常常发育不同几何形态与构造特征的隆起带或冲起构造带, 未叠置断层带常常发育拉伸的菱形冲起构造、高叠置主断层带形成“S”型冲起构造, 压扭性走滑断层叠置带常发育平行四边形或箱状冲起构造, 伴随主断层间隔距离的增大冲起构造带几何形态逐渐转变为平行四边形且断层倾角显著增大(Richard et al., 1995; McClay and Bonora, 2001; Mitra and Paul, 2011)。基底走滑主断层间差异叠置性/弯曲性导致走滑冲起构造形成明显不同的旋转变形分量, 如: 从低叠置压扭性断阶(约30°叠置夹角)导致形成冲起构造带7°逆时针旋转变形到高叠置断阶(约150°叠置夹角)导致形成冲起构造带16°逆时针旋转变形(图6a; McClay and Bonora, 2001), 同时压扭性断阶/弯曲带冲起构造与逆断层由外向内的生长过程可能也具有差异性。

自然界复杂动力学作用通常导致沿走滑剪切构造带应力‒应变机制走向变化, 如: 纯走滑剪切、张性/挤压走滑剪切等变形, 砂箱物理模拟实验广泛揭示拉张或挤压方向(相对于主走滑断裂带)对走滑构造体系分段性及其走滑转换带构造变形具有重要控制作用, 尤其是主应力场方向与走滑断裂带相关性(Zwaan and Schreurs, 2016)。右旋走滑剪切作用条件下, (右阶)相叠置基底断层更加容易走向传播生长, 形成以离散性走滑断层为典型特征的走滑转换带(图6b); 与之相反, 左旋走滑剪切作用下相叠置基底断层更加容易相背生长。叠置基底断层间先存构造通常在晚期走滑剪切变形作用过程中再活化, 但它们普遍继承早期构造的几何学特征。尤其伴随拉张剪切主应力场与基底走滑断裂夹角减小, 导致走滑剪切构造带走向分段性减弱、且走滑转换带几何学规模明显减小(Zwaan et al., 2016)。

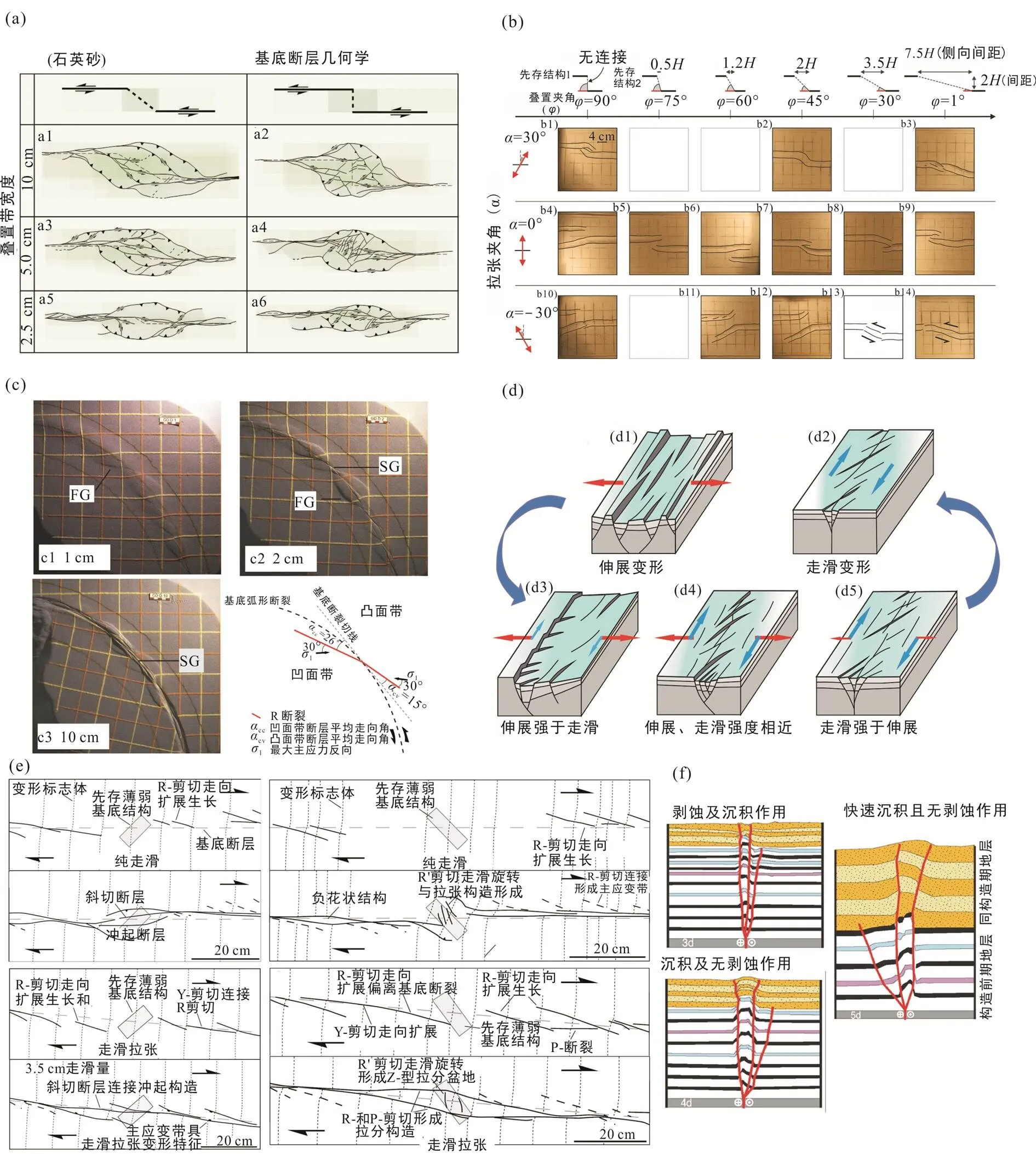
(a) 砂箱物理模拟实验中基底断裂几何学(即叠置性、断阶间距)与冲起构造特征, 伴随基底断裂间距(即断阶间距)增大冲起构造规模明显增大、且内部构造变形复杂化增强(McClay and Bonora, 2001); (b) 走滑剪切主应力场方向与基底断裂带相关性控制走滑转换带变形特征(Zwaan and Schreurs, 2016)。右旋走滑剪切作用条件下, (右阶)相叠置基底断层更加容易走向传播生长, 形成以离散性走滑断层为主的走滑转换带。(c) 受控于弧形主走滑断层两侧差异性应力‒应变机制, 基底走滑断裂内凹侧较早形成吕德尔剪切断裂、且具有较高发育程度(Dufrechou et al., 2011); (d) 伸展与走滑作用的强弱配比关系控制影响着断裂发育特征(陈兴鹏等, 2019), 走滑作用强于拉张伸展作用导致平面上张性断层、P和R剪切发育形成走滑剪切带。(e) 非均一性砂箱物质导致走滑剪切带应力‒应变走向变化, 线性软弱带不同展布方向对纯剪或张剪性构造变形作用过程的影响(Dooley and Schreures, 2012)。(f) 浅表构造剥蚀与沉积作用过程对走滑剪切变形作用的控制影响作用(Guerroue and Cobbold, 2006), 同构造剥蚀和沉积作用导致走滑构造带断层倾角普遍增大、走滑隆起“花状”结构带宽度显著减小。

砂箱物质非均一性特征, 如: (与走滑剪切带斜交)先存构造变形带或软弱带等, 常常导致走滑剪切带沿该非均一结构带发生应力‒应变集中(Mann et al., 2007; Holohan et al., 2008; Dooley and Schreures, 2012), 伴随走滑剪切位移逐渐增大形成典型的成对弯曲断层系统。沿走滑剪切带展布的非均一性砂箱物质分布特征(如: 双圆柱软弱带、线性软弱岩带等)对剪切带构造变形分带性具有重要的控制和影响作用(图6e)。当线性软弱岩带与砂箱基底断裂带具逆时针或顺时针45°斜向夹角时, 沿软弱岩带普遍会形成“S”型或平行四边形冲起带, 砂箱走滑剪切破裂沿该带周围传播、合并形成主走滑变形带, 但后者通常还会形成较高角度的R′剪切破裂。当走滑剪切变为张性走滑剪切时, 其相关冲起构造带具有相对较小的隆起程度和变形范围、同时受晚期斜切断裂(以RL型为主)切割, 主走滑变形带(PDZ)末端普遍形成不同形态的拉分盆地。当砂箱物质包含多个非均一结构带(如: 膏盐体或膏盐带)时, 由于非均一软弱结构带未直接就位于基底断裂带上方导致通常形成贯通断层带切割砂箱物质, 低角度R剪切破裂逐渐形成、叠置与合并形成主走滑变形带(PDZ) 和相对较窄的张性位错与张性弯曲断层带, 尤其是形成典型的张性拉分盆地。浅表作用过程(如: 剥蚀与沉积)通过控制浅部物质负载作用过程控制影响走滑剪切构造带应力‒应变条件, 从而对其变形作用过程具有重要影响性(Guerroue and Cobbold, 2006; Moustat and Khalil, 2017)。浅表剥蚀和沉积作用通常导致走滑断层埋深停止活动生长、部分断层持续走滑切割同沉积地层或剥蚀暴露, 总体上断层倾角普遍增大、走滑隆起“花状”结构带宽度显著减小(图6f)。

总体而言, 走滑剪切构造系统分段性及其走滑转换带差异变形特征受控于基底走滑断层应力‒应变条件沿走向差异变化的特性, 其走向差异变化特性主要控制因素包括: 基底断层几何学(如: 弯曲/叠置性、间隔性、弧形断层等)、砂箱动力学特性(如: 纯走滑剪切、张性/挤压走滑剪切等)、(非)均质性砂箱物质特征(如: 黏土和膏岩等)、基底非均一性(如: 塑性基底物质几何学等)等。

3 典型走滑构造实例砂箱物理模拟实验

3.1 维也纳盆地低角度拉分走滑剪切构造砂箱物理模拟实验

维也纳盆地是位于中欧东部、东阿尔卑斯与西喀尔巴阡褶皱带之间的左旋走滑拉分盆地, 具有波希米亚和古生界至中生界双重基底, 其基底埋藏最大达到9000～10000 m; 盆地拉张走滑快速沉降开始于中新世, 上新世盆地发生部分构造反转(Horvath and Clotingh, 1996)。区域地质填图揭示空间上维也纳盆地周缘主要以雁列式、斜向拉张正断层系统为主(Hinsch et al., 2005; Arzmuller et al., 2006), 这与拉分走滑剪切砂箱物理模拟实验所揭示盆地边缘变形区域发育典型的雁列式、斜向拉张正断层系统相一致(图7), 而区别于纯走滑剪切砂箱物理模型实验结果(Dooley and McClay, 1997; Wu et al., 2009)。

剖面结构上, 维也纳盆地边缘带断裂系统具有明显的负花状结构特征, 同时由于后期叠加反转挤压变形导致部分断层具有逆断层特征, 揭示出剖面结构上的非对称性(图7d)。伴随盆地内持续的同沉积充填, 维也纳盆地具有非对称性地堑结构(Arzmuller et al., 2006), 同时形成典型的北西和南东地区的双沉积中心, 其最大沉积中心厚度达到4～6 km(图7d); 双沉积中心被中央高地及其发育的断层系统切割分离, 这与砂箱物理模拟实验中双沉积中心一致性。伴随持续的拉分走滑剪切构造变形, 砂箱物理模拟实验中物质发生非对称性拉张变形, 盆地边缘率先形成系列雁列式、斜向拉张正断层系统; 同时在基底断裂弯曲带分别形成方向相反的两个沉积中心, 沉积中心在拉张走滑中后期快速形成, 而区别于纯走滑剪切物理模型的单一沉积中心特征(Dooley et al, 2004; Wu et al., 2009)。早期走滑剪切沿中央主走滑变形位移带(PDZ)形成的雁列式断裂/破裂, 受后期持续拉张走滑剪切控制逐渐形成相对较窄的中央地堑系统, 分割双沉积中心, 同时由于双沉积中心的发育导致拉分走滑剪切盆地具有明显较宽的盆地几何学特征。需要指出的是, 维也纳盆地中双沉积中心形成演化可能伴随大规模物质的旋转变形, 这与盆地中央大量走滑断层侧向叠置和斜列旋转生长等特征相一致(图7c), 但在拉分走滑剪切物理模拟实验中模型中央主走滑变形位移带缺少相应变形特征, 其差异性可能受控于物理模型的单一基底断层模式(即吕德尔剪切模式)。

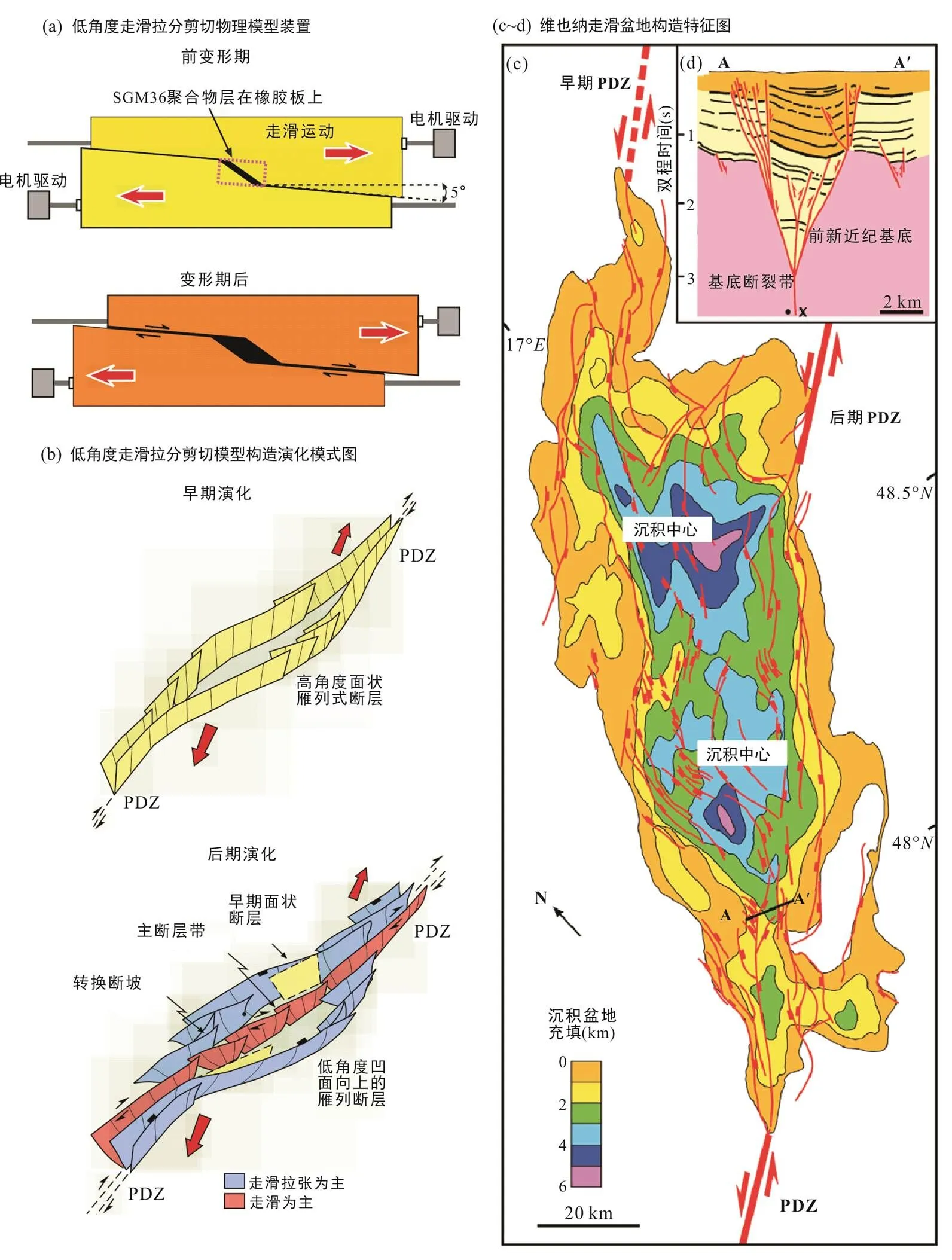
(a) 低角度(5°)拉分走滑剪切物理模型装置图(Wu et al., 2009); (b) 低角度走滑拉分剪切模型构造演化模式图(Wu et al., 2009), 揭示早期阶段形成较窄的面状高角度倾角的、雁列式斜向拉张正断层特征, 后期发育典型的沿中央主位移带走滑断层体系分割盆地沉积中心; (c, d) 维也纳盆地典型构造特征图(Arzmuller et al., 2006), 空间上揭示维也纳盆地边缘雁列式、斜向拉张正断层特征, 同沉积充填厚度进一步揭示拉分走滑剪切的双沉积中心特征。

3.2 莺歌海盆地弧形走滑构造砂箱物理模拟实验

莺歌海盆地位于古特提斯和环太平洋构造域的交接转换地带, 新生代印‒藏陆陆碰撞和太平洋板块俯冲所导致的印支地块和华南地块之间的多期次相对运动, 控制着莺歌海盆地形成演化(孙向阳和任建业, 2003; Zhu et al., 2009; 谢玉洪等, 2015; 宫伟等, 2017), 尤其印支地块旋转挤出过程所引起的延伸长度超过1000 km的、红河韧性走滑剪切带(Leloup et al., 1995)。红河断裂带在莺歌海盆地内分支为两条盆地边界断层和多条盆地内部断层带、具弥散性变形特征, 如: 马江断裂带、斋河断裂等; 同时断裂入海后由北西走向转变为近南北向、平面上具弧形弯曲特征(图1)。

莺歌海盆地地层可大致分为(1)古生界‒中生界前裂谷期基底层系、(2)始新世‒中中新世裂谷同期湖相、河流相和部分海相层系和(3)中新世以来的裂谷后期海相碎屑岩。新生代早期红河断裂左旋走滑挤出过程, 导致莺歌海盆地发育大量走滑断层系统, 在莺歌海盆地西侧走滑相关断层系统普遍具有面状断层结构、倾角约40°～60°, 如: 红河断层(图8f)。相对比的是, 在莺歌海盆地东侧普遍发育高角度‒垂直倾角的走滑断裂体系, 且常见凸面向上断层组成的“棕榈树状”花状构造。莺歌海盆地东西两侧发育走滑断裂特征的差异性与弧形走滑砂箱物理模型变形特征相一致, 即弧形构造变形内弧带断层倾角较缓、逆冲特征较突出, 外弧带断层倾角高陡、走滑剪切特征明显(图8b)。

区域哀牢山‒红河韧性走滑断裂的向南延伸进入莺歌海盆地, 在盆地西北部地区断层具有明显的右阶雁列式展布特征, 这与弧形弥散性走滑物理模型顶面结构一致。伴随持续走滑挤出与盆地演化过程, 基底走滑断裂体系普遍未切割上覆(裂谷后期)层系, 如: 红河断裂和Song Lo断层普遍未切割上新统黄流组(5.3 Ma)(图8e-f)。砂箱物理模型中通过硅胶层系模拟自然界高塑性层系, 如: 膏盐层系、超压泥质岩层系等, 它们明显限制着深部走滑断层的垂向生长过程, 导致深部断层终止于高塑性层系, 仅部分强走滑变形断层在物理模型表面出露。物理模拟实验结果与莺歌海盆地对比, 揭示出区域裂谷后期快速沉积的黄流组‒莺歌海组对于早期走滑断裂垂向生长过程具有一定的限制性。由于上新统(即5.5 Ma以来)红河断裂带仍然具有较强烈的走滑剪切变形作用, 其走滑量约为60～100 km(Rangin et al., 1995; Zhu et al., 2009), 因此受到上覆裂谷后期塑性层系限制、莺歌海盆地走滑断裂变形仅切割中新统三亚组(图8d-f)。需要指出的是, 物理模型中未考虑同裂谷期积期快速沉积充填(即同构造沉积作用), 在区域地震剖面中能够识别出三亚组‒黄流组典型楔状地层特征, 这与物理模型剖面结构具有一定的差异性。综上所述, 莺歌海盆地新生代构造演化过程及其特征受控于以哀牢山‒红河弧形断裂系统的弥散性左旋走滑挤出作用过程。

4 讨论与结论

自20世纪初以来, 砂箱物理模拟手段方法学的兴起与发展为我们解译走滑构造系统演化过程及其动力学机制等提供了独立有效的手段。基于吕德尔剪切和弥散性剪切物理模型实验揭示, 走滑变形位移带普遍发育五类断裂/破裂体系, 即R型破裂、R′型破裂、P剪切、张破裂和Y型破裂, 尤其是在弥散性剪切变形过程中发育大量的RL和RL′型斜切剪破裂, 伴随走滑剪切作用物质发生大规模走滑旋转、产生断层侧向斜列叠置和传播生长。浅表走滑构造系统变形过程中, 基底断层几何学(弯曲/叠置性、间隔性等)、砂箱动力学特性(纯走滑剪切、拉分走滑和挤压走滑剪切)、非均质性砂箱物质特征(黏土和膏岩等)、基底非均一性(塑性基底物质几何学等)等对走滑构造变形过程具有明显控制作用。弥散性弧形走滑剪切物理模拟揭示莺歌海盆地新生代构造演化过程及其特征主要受控于以哀牢山‒红河弧形断裂系统的弥散性左旋走滑挤出作用过程。

砂箱物理模拟实验对于浅表走滑构造系统解译具有独特优势的同时, 它也具有与生俱来的缺点, 如: 简化的砂箱模型装置、地层力学机制和动力学条件等。尤其是, 由于含水特殊性问题导致走滑剪切物理模拟过程中广泛使用的湿黏土材料粘聚强度变化、可重复性等仍需完善, 但这些缺陷性并不意味着砂箱物理模拟的不可靠性和非科学性。近百年来, 大量砂箱物理模拟实验研究揭示走滑构造系统变形过程中多因素耦合的控制性, 但迄今为止许多走滑变形细节过程仍然缺少有效的机制模型研究, 如: 温‒压相关属性、流体超压与充注过程等。我国复杂板内‒板缘动力学背景中, 多期走滑构造反转与构造叠加、多期旋转动力拉张走滑构造过程等物理模拟实验的开展, 是当前构造物理模拟学界急需开展的前缘科学问题之一, 尤其是我国东部海域走滑构造盆地群普遍发育同构造沉积地层, 针对它们的地壳浅表剥蚀‒沉积互馈机制如何应用于实际自然界原型和砂箱物理模型的研究有待更加深入开展, 如: 源‒汇体系物质搬运方式与机制、稳态/非稳态浅表剥蚀‒沉积作用等。伴随砂箱物理模拟手段在走滑构造系统变形过程研究的广泛使用, 其挑战性在于如何把创新性砂箱装置、全时三维监测和应变量化等手段融入砂箱物理模型中有效解译地壳浅表走滑构造系统变形的实际问题, 从而使其在地震灾害机理、油气勘探等方面发挥越来越重要的作用。

(a) 莺歌海盆地弧形弥散性走滑模型装置图; (b) 弧形走滑最终阶段顶面和切片特征图, 沿弧形剪切带物质顶面走滑断裂雁列式展布、垂直剖面上内弧带与外弧带断层倾角和走滑逆冲变形强度具有明显差别; (c, d, e, f) 莺歌海盆地典型构造特征图, 揭示莺歌海盆地东西两侧走滑断裂具有几何学和运动学差异性, 同时走滑断裂系统受控于走滑作用和泥质岩层系等控制普遍未切割裂谷后期层系。

感谢中国石油大学(华东)李伟博士和另一位匿名审稿专家对文章提出宝贵的修改意见。

陈发景, 汪新文, 陈昭年. 2011. 伸展断陷中的变换构造分析. 现代地质, 25(4): 617–625.

陈兴鹏, 李伟, 吴智平, 徐长贵, 任健. 2019. “伸展‒走滑”复合作用下构造变形的物理模拟. 大地构造与成矿学, 43(6): 1106–1116.

邓宾, 黄瑞, 马华灵, 何宇, 赖东, 姜磊, 刘树根. 2018. “从源到汇”: 褶皱冲断带前陆盆地系统砂箱物理模型浅表作用研究. 大地构造与成矿学, 42(3): 431–444.

邓宾, 赵高平, 万元博, 黄瑞, 王兴建, 刘树根. 2016. 褶皱冲断带构造砂箱物理模型研究进展. 大地构造与成矿学, 40(3): 446–464.

邓起东, 程绍平, 马翼, 杜鹏. 2014. 青藏高原地震活动特征及当前地震活动形势. 地球物理学报, 57(7): 2025–2042.

宫伟, 李朝阳, 姜效典. 2017. 青藏高原隆升与南海开启: 南海西北部盆‒山耦合体系. 地学前缘, 24(4): 268–283.

国土资源部矿产资源储量司. 2013 年全国油气矿产储量通报. 北京: 国土资源部信息中心.

李艳友, 漆家福, 周赏. 2017. 走滑构造差异变形特征及其主控因素分析——基于砂箱模拟实验. 石油实验地质, 39(5): 711–715.

马宝军, 漆家福, 牛树银, 孙爱群, 曹爱峰, 孙志信. 2009. 统一应力场中基底断裂对盖层复杂断块变形的影响——来自砂箱实验的启示. 地学前缘, 16(4): 105–116.

漆家福. 2007. 裂陷盆地中的构造变换带及其石油地质意义. 海相油气地质, 12(4): 43–52.

任健, 官大, 陈兴鹏, 刘朋波. 2017. 走滑断裂叠置拉张区构造变形的物理模拟及启示. 大地构造与成矿学, 41(3): 455–465.

孙向阳, 任建业. 2003. 莺歌海盆地形成与演化的动力学机制. 海洋地质与第四纪地质, 23(4): 45–50.

童亨茂, 龚发雄, 孟令箭, 赵宝银. 2018. 渤海湾盆地南堡凹陷边界断层的“跃迁”特征及其成因机制. 大地构造与成矿学, 42(3): 421–430.

童亨茂, 赵宝银, 曹哲, 刘国玺, 顿小妹, 赵丹. 2013. 渤海湾盆地南堡凹陷断裂系统成因的构造解析. 地质学报, 87(11): 1647–1661.

吴智平, 薛雁, 颜世永, 宿雯, 王昕, 徐长贵, 周心怀. 2013. 渤海海域渤东地区断裂体系与盆地结构. 高校地质学报, 19(3): 463–471.

肖阳, 邬光辉, 雷永良, 陈婷婷. 2017. 走滑断裂带贯穿过程与发育模式的物理模拟. 石油勘探与开发, 44(3): 340–349.

谢玉洪, 李绪深, 童传新, 刘平, 吴红烛, 黄志龙. 2015. 莺歌海盆地中央底辟带高温高压天然气富集条件、分布规律和成藏模式. 中国海上油气, 27(4): 1–12.

徐长贵. 2016. 渤海走滑转换带及其对大中型油气田形成的控制作用. 地球科学, 41(9): 1548–1560.

曾融生, 孙为国. 1992. 青藏高原及其邻区的地震活动性和震源机制以及高原物质东流的讨论. 地震学报, 14: 531–563.

Adam J, Klinkmuller M, Schreurs G and Wieneke B. 2013. Quantitative 3D strain analysis in analogue experiments simulating tectonic deformation: Integration of X-ray computed tomopgraphy and digital volume correlation techniques., 55: 127–149.

An L J. 1998. Development of fault discontinuities in shear experiments., 293: 45–59.

An L J and Sammis C G. 1996. Development of strike-slip faults: Shear experiments in granular materials and clay using a new technique., 18: 1061–1077.

Arch J, Maltman A J and Knipe R J. 1988. Shear zone geometries in experimentally deformed clays: The influence of water content, strain rate and primary fabric., 10: 91–99.

Arzmuller G, Buchta S, Ralbovsky E and Wessely G. 2006. The Vienna Basin // Golonka J and Picha FJ. The Carpa­thians and Their Foreland: Geology and Hydrocarbon Resources., 84: 191–204.

Atmaoui N, Kukowski N, Stockhert B and Konig D. 2006. Initiation and development of pull-apart basins with Riedel shear mechanism: Insights from scaled clay experiments., 95: 225–238.

Bartlett W L, Friedman M and Logan J M. 1981. Experimental folding and faulting of rocks under confining pressure, Part IX. Wrench faults in limestone layers., 79: 255–277

Cloos H. 1928. Experimente zur inneren Tektonik.,B, 12: 609–621.

Colletta B, Letouzey J, Ballard J F and Balle P. 1991. Computerized X-ray tomography analysis of sandbox models: examples of thin-skinned thrust systems., 19(11): 1063–1067.

Davis D, Suppe J and Dahlen F A. 1983. Mechanics of fold-and-thrust belts and accretionary wedges., 88(B12): 1153–1172.

Dooley T and McClay K R. 1997. Analog modeling of pull-apart basins., 81: 1804–1826.

Dooley T, Monastero F, Hall B, McClay K R and Whitehouse P. 2004. Scaled sandbox modelling of transtensional pull-apart basins: Applications to the Cosogeothermal system., 28: 637–641.

Dooley T and Schreurs G. 2012. Analogue modelling of intraplate strike-slip tectonics: A review and new experimental results., 574–575: 1–71.

Dufrechou G, Odonne F and Viola G. 2011. Analogue models of second-order faults genetically linked to a circular strike-slip system., 33: 1193–1205.

Eisenstadt G and Sims D. 2005. Evaluating sand and clay models: Do rheological differences matter., 27: 1399–1412.

Gapais D, Fiquet G and Cobbold P R. 1991. Slip system domains, 3. New insights in fault kinematics from plane-strain sandbox experiments., 188: 143–157.

Guerroue E L and Cobbold P R. 2006. Influence of erosion and sedimentation on strike-slip fault systems: Insights from analogue models., 28: 421–430.

Harding T P. 1974. Petroleum traps associated with wrench faults., 58: 1290–1304.

Hinsch R, Decker K and Peresson H. 2005. 3-D seismic interpretation and structural modeling in the Vienna Basin: Implications for Miocene to recent kinematics., 97: 38–50.

Holohan E P, van Wyk de Vries B and Troll V R. 2008. Analogue models of caldera collapse in strike-slip tectonic regimes., 70(7): 773–796.

Horvath F and Clotingh S. 1996. Stress-induced late-stage subsidence anomalies in the Pannonian Basin., 266: 287–300.

Hubbert M K. 1937. Theory of scale models as applied to the study of geologic structures., 48: 1459–1520.

Koyi H. 1997. Analogue modelling: From a qualitative to a quantitative technique—A historical outline., 20(2): 223–238.

Leever K A, Cabrielsen R H, Sokoutis D and Willingshofer E. 2011. The effect of convergence angle on the kinematic evolution of strain partitioning in transpressional brittle wedges: Insight from analog modeling and high-resolution digital image analysis., 30, TC2013, doi: 10.1029/2010TC002823.

Leloup P H, Lacassin R, Tapponnier P, Scharer U, Zhong D L, Liu X H, Zhang L S, Ji S C and Trinh P T. 1995. The Ailao Shan-Red River shear zone (Yunnan, China), Tertiary transform boundary of Indochina., 251: 3–84.

Lohrmann J, Kukowski N, Adam J and Oncken O. 2003. The impact of analogue material properties on the geometry, kinematics, and dynamics of convergent sand wedges., 25(10): 1691–1711.

Mann P, Demets C and Wiggins-Grandison M. 2007. Toward a better understanding of the Late Neogene strike-slip restraining bend in Jamaica: Geodetic, geological and seismic constraints // Cunningham W D and Mann P. Tectonics of Strike-slip Restraining and Releasing Bends.,,, 290: 239–253.

Marone C. 1998. Laboratory-derived friction laws and their application to seismic faulting., 26: 643–696.

McClay K R and Bonora M. 2001. Analog models of restraining stepovers in strike-slip fault systems., 85: 233–260.

Misra S, Mandal N and Chakraborty C. 2009. Formation of Riedel shear fractures in granular materials: Findings from analogueshear experiments and theoretical analyses., 471: 253–259.

Mitra S and Paul D. 2011. Structural geometry and evolution of releasing and restraining bends: Insights from laser-scanned experimental models., 95(7): 1147–1180.

Morgenstern N R and Tchalenko J S. 1967. Microscopic structures in kaolin subjected to direct shear., 17: 309–328.

Moustafa A R and Khalil S M. 2017. Control of compressionaltransfer zones on syntectonic and post-tectonic sedimen­tation: Implications for hydrocarbon exploration., 174: 336–352.

Naylor M, Mandl G and Sijpesteijn C K. 1986. Fault geometries in basement-induced wrench faulting under different initial stress states., 8: 737–752.

Panien N, Schreurs G and Pfiffner A. 2006. Mechanical behaviour of granular materials used in analogue modelling: Insights from grain characterisation, ring-shear tests and analogue experiments., 28: 1710–1724.

Rangin C, Klein M, Roques D, Le Pichon X and Trong L V. 1995. The Red River Fault system in the Tonkin Gulf, Vietnam., 243: 209–222.

Richard P and Cobbold P R. 1990. Experimental insights into partitioning of fault motions in continental convergent wrench zones., 4(2): 35–44.

Richard P, Naylor M A and Koopman A. 1995. Experimental models of strike-slip tectonics., 1: 71–80.

Riedel W. 1929. Zur Mechanik geologischer Brucherscheinungen.,B: 354–368.

Rosas F M, Duarte J C, Schellart W P, Tomas R, Grigorova V and Terrinha P. 2012. Thrust-wrench interference between major active faults in the Gulf of Cadiz (Africa-Eurasia plate boundary, offshore SW Iberia): Tectonic implicationsfrom coupled analog and numerical modeling., 548–549: 1–21.

Schellart W P and Nieuwland D A. 2003. 3-D evolution of a pop-up structure above a double basement strike-slip fault: Some insights from analogue modeling // Nieuwland D A. New insights into Structural Interpretation and Modelling.,,: 169–179.

Schreurs G. 2003. Fault development and interaction in distributed strike-slip shear zones: An experimental approach // Storti F, Holdsworth R E and Salvini F. Intraplate Strike-slip Deformation Belts.,,, 210: 35–52.

Schreurs G and Colletta B. 1998. Analogue modelling of faulting in zones of continental transpression and transtension // Holdsworth R E, Strachan R A and Dewey J F. Continental Transpressional and Transtensional Tectonics., 135: 59–79.

Soto R, Martinod J and Odonne F. 2006. Influence of early strike-slip deformation on subsequent perpendicular shortening: An experimental approach., 29: 59–72.

Storti F, Holdsworth R E and Salvini F. 2003. Intraplate strike-slip deformation belts.,,, 210: 1–14.

SyLvester A G. 1988. Strike-slip faults., 100: 1666–1703.

Tchalenko J S. 1970. Similarities between shear zones of different magnitudes., 81: 1625–640.

Tong H M, Koyi H, Huang S and Zhao H T. 2014. The effect of multiple pre-exiting weaknesses on formation and evolution of faults in extended sandbox models., 626: 197–212.

Ueta K, Tani K and Kato T. 2000. Computerized X-ray tomography analysis of three-dimensional fault geometriesin basement-induced wrench faulting., 56: 197–210.

Wigner E P. 1960. The unreasonable effectiveness of mathematics in the natural sciences., 13(I): 1–14.

Wilcox R E, Harding T P and Seely D R. 1973. Basic wrench tectonics., 57: 74–96.

Withjack M O, Schlische R and Henza A A. 2007. Scaled experimental models of extension: Dry sand vs. wet clay., 49(8): 31–49.

Woodcock N H. 1986. The role of strike-slip fault systems at plate boundaries., ser. A. 317: 13–29.

Woodcock N H and Schubert C. 1994. Continental strike- slip tectonics // Hancock P L. Continental Tectonics. Pergamon Press, Oxford: 251–263.

Wu J E, McClay K, Whitehouse P and Dooley T. 2009. 4D analogue modelling of transtensional pull-apart basins., 26: 1608–1623.

Zhu M Z, Graham S and McHargue T. 2009. The Red River Fault zone in the Yinggehai Basin, South China Sea., 476: 397–417.

Zuza A V, Yin A, Lin J and Sun M. 2017. Spacing and strength of active continental strike-slip faults., 457: 49–62.

Zwaan F and Schreurs G. 2016. How oblique extension and structural inheritance influence rift segment interaction: Insights from 4D analog models., 5(1): 119–138.

Zwaan F, Schreurs G and Adam J. 2018. Effects of sedimentationon rift segment evolution and rift interaction in orthogonaland oblique extensional settings: Insights from analogue models analysed with 4D X-ray computed tomography and digital volume correlation techniques., 171: 110–133.

Zwaan F, Schreurs G, Naliboff J and Buiter S. 2016. Insights into the effects of oblique extension on continental rift interaction from 3D analogue and numerical models., 693: 239–260.

A Review on Analogue Modelling of Strike-slip Tectonics

XIE Yuhong

(100010,)

Strike-slip deformation in the shallow crust occurs in diverse geodynamics and exhibits complex geological features, such as earthquakes, hydrocarbon accumulation, etc. Since the 1900s, analogue modelling has become a powerful and indispensable tool which can provide an integrated picture of strike-slip deformation based on self-organization and unreasonable effectiveness of tectonics. In nature, the strike-slip system can be divided into the boundary transform and intraplate strike-slip shears in geodynamics, and divided into bend-type and stepover-type strike-slip shears in geometry. Based on the analogue modelling of Riedel and distributed strike-slip deformation, five type shears or strike-slip faults across the principal displacement zone (PDZ) can further be recognized which include R-shears, R′-shears, P-shears, tensile shear and Y-shear. RL- and RL′-shears are common in distributed strike-slip deformation. Previous analogue modeling researches have explored the role of main parameters governing strike-slip deformation, including the properties of basement fault (bend and stepover), kinematics (pure strike-slip, transpression and transtension), surface processes (erosion and sedimentation), the properties of material (wet-clay, silicone), and inhomogeneous basement etc. Nowadays, analogue modelling has become a critical gateway in researches of mechanical and structural evolution of strike-slip system in the shallow crust, as well as in the earthquake and hydrocarbon exploration.

Analogue modelling; strike-slip deformation; Riedel strike-slip shear; distributed strike-slip shear

P542

A

1001-1552(2021)06-1127-019

10.16539/j.ddgzyckx.2021.02.015

2020-05-26;

2020-11-01;

2021-04-27

国家科技重大专项(2016ZX05024)资助。

谢玉洪(1961–), 男, 教授级高级工程师, 从事海洋油气勘探、开发生产科研与工程管理工作。Email: xieyh@cnooc.com.cn