基于奇异值分解的激光超声晶粒尺寸检测研究

彭 昊,朱振格,宋学勇,徐亚诚,殷安民,束学道,王 英,左锦荣,谢重阳,谯自健

(1.宁波大学机械工程与力学学院,浙江 宁波 315211;2.浙江省零件轧制成形技术研究重点实验室,浙江 宁波 315211;3.宁波市数字化制造技术重点实验室,浙江 宁波 315211)

1 引 言

金属材料的晶粒尺寸对其力学性能有着直接的影响[1]。目前传统的晶粒尺寸检查方式为金相法、扫描电镜和EBSD(Electron Backscatter Diffraction),虽然检查精度高但其繁琐的检查过程无法满足快速在线检测需要[2-3]。金属材料生产过程中的晶粒尺寸在线无损检测技术是目前企业实现数字化制造和质量在线监控急需且不可或缺的技术之一[4]。

激光超声是一种基于传统接触式超声检测传感器的延伸[5],其具有非接触、远距离检测、频带宽、可检性和可达性好等许多传统测试方法不可比拟的优点,弥补了常规超声需要耦合剂、电磁超声检测距离短而很难实现在线检测的缺点,为晶粒尺寸在线无损检测提供了一种切实可行的方法。

目前,国内外学者在金属材料激光超声晶粒尺寸检测方面已经做了大量的工作,如Sundin S[6]等人研究了激光超声技术用于检测工业低碳钢的晶粒尺寸。采用散射理论的分析方法,直接从超声信号中计算出了衰减量与晶粒尺寸的绝对值,不需要在衰减量与晶粒尺寸之间进行任意参数拟合或校准曲线。C.S.Lim[7]等人使用激光超声检测技术,在实验室对热轧钢板的晶粒尺寸与超声衰减系数之间的关系进行了评估,并对Fabry-Perot干涉仪进行了优化以提高信噪比,已经确定了在线测量生产线中热轧钢板晶粒尺寸的可能性。李雄兵[8]等人研究了不考虑厚度的超声方法评价核电站结构材料的晶粒尺寸,提出了一种利用透射系数和反射系数来计算超声衰减率系数的新方法。但是,在提高激光超声晶粒尺寸检测精度方面,尤其是在平均晶粒尺寸相近时,如何进行精确检测方面的研究还较少。

本文采用激光超声无损检测技术,选用各向异性较小的冷轧低碳钢为研究对象,首先通过激光超声二次回波、三次回波的幅值衰减来计算冷轧低碳钢试样的平均晶粒尺寸,并采用扫描电镜(Scanning Electron Microscope,SEM)对平均晶粒尺寸的计算准确性进行验证。然后通过奇异值分解降噪方法对激光超声的频域信号进行降噪分析,对激光超声检测平均晶粒尺寸的计算方法进行了优化,提高了平均晶粒尺寸的检测精度,并分析了晶粒尺寸分布对激光超声晶粒尺寸检测的影响。

2 试验材料与方法

2.1 试验材料

实验材料为国产商用冷轧低碳钢轧制板材,实验材料直接从工业生产的卷材上直接切取得到,试样板材厚度为2 mm。其化学成分如表1所示。

表1 冷轧低碳钢成分/%Tab.1 Cold rolled low carbon steel composition/%

为了消除化学成分、第二相、热轧工艺、析出、各向异性和位错等因素对激光超声实验结果的影响,并得到对同种样品的不同的晶粒尺寸,将试样切割成长和宽分别为 75 mm×65 mm 的 25份实验样品在电阻马弗炉中分别进行热处理,热处理温度初始温度为800 ℃,温度梯度为20 ℃,保温时间以2 min开始,每2 min递增,冷却方式统一采用空冷,其详热处理工艺如表2所示。实验材料热处理后,经镶样、磨样、抛光、腐蚀制备成金相试样,金相样品腐蚀剂为4 %硝酸酒精,腐蚀时间为10 s,清洗样品后采用日立SU 5000热场发射型扫描电子显微镜(SEM)观察试样显微组织。

表2 热处理工艺Tab.2 Heat treatment process

本文使用Image J软件测量所划横线长度并计算横线穿过晶粒尺寸个数,得到试样平均晶粒尺寸,为避免一条横线随机性过大和过多横线对同一晶粒重复测量,本实验在SEM所测得的显微组织图上共划10条等距离横线,相邻横线距离大于两倍平均晶粒尺寸[10]。

2.2 激光超声检测系统

本实验采用如图1所示的激光超声实验室检测系统,实验所采用的脉冲激光器为调Q的Nd∶YAG激光器,激发激光器的脉冲时间宽度为12 ns,脉冲能量为200 mJ,波长为532 nm。激光超声接收系统为TWM-532双波干涉仪,功率200 mW,波长为532 nm,检测带宽为200 MHz。为了消除超声信号采集误差,每块样品分别进行3次激光超声检测,每次检测信号进行128次平均。

图1 激光超声实验室检测系统Fig.1 Schematic diagram of laser ultrasonic laboratory testing

3 试验结果与讨论

3.1 晶粒尺寸检测结果

由扫描电镜测得的典型样品微观组织如图2所示,可见,所有样品的微观组织为等轴晶,晶粒尺寸分布较为类似,且未发现明显异常大的晶粒,肉眼很难区分样品平均晶粒尺寸的大小。

图2 典型样品微观组织图Fig.2 Microstructure of typical samples

使用Image J软件基于割线法(割线方向为水平方向,与激光超声检测接收方向一致)测得试样晶粒尺寸,并依照测得的平均晶粒尺寸大小递增顺序将各个样品依次编号,样品的晶粒尺寸分布图如图3所示,样品的晶粒尺寸信息列于表3中。可见,样品的最小平均晶粒尺寸为12.59 μm,最大平均晶粒尺寸为16.55 μm,极值差距仅为3.96 μm。

表3 实验样品晶粒尺寸Tab.3 Grain size of the samples

图3 晶粒尺寸分布图Fig.3 Grain size distribution

同时,采用不均匀性因子Z[10]反映的实验样品晶粒尺寸分布特性。

(1)

式中,Z为不均匀性因子；Dmax为最大晶粒尺寸；Dk为出现几率最高的晶粒尺寸。

根据图3可以得到出现几率最高的晶粒尺寸范围,将其平均值作为出现频率最高的晶粒尺寸Dk,由此计算得到晶粒不均匀。

由表3可知实验样品的晶粒尺寸出现最多的范围是6.5～9.5 μm之间,最大晶粒尺寸较大,其范围在43～55 μm之间,实验样品的不均匀性因子均值为6.3,最小因子为20号样品的4.61,最大因子为4号样品的8.50。造成不均匀性因子较大的主要原因是样品有少数个别的大晶粒存在。

3.2 幅值法计算晶粒尺寸

当检测系统确定后,样品平均晶粒尺寸直接影响实际测得的超声波衰减系数。本节衰减系数计算采用幅值法,计算超声信号时域衰减系数,首先,对每一个样品的超声信号提取第二次底面回波(3P)、第三次底面回波(5P)的幅值(纵坐标),典型的信号图如图4所示。

图4 典型超声信号图Fig.4 Typical ultrasonic signal

然后,将提取到的波峰(纵坐标)代入公式[9]计算超声衰减系数:

(2)

式中,α为超声衰减系数；A2为二次回波3P的幅值；A3为三次回波5P的幅值；L为试样平均厚度。

由式(2)计算得到的超声衰减系数与使用Image J软件测得的平均晶粒尺寸进行线性拟合,拟合效果如图5所示。

图5 衰减系数与晶粒尺寸拟合图Fig.5 Fitting diagram of original signal attenuation coefficient and grain size

由图5可见,超声波衰减随着晶粒尺寸的增大而增大,但有许多点呈发散趋势,趋于拟合曲线的点并不多,拟合优度仅为0.61,拟合偏离度方差为0.57,波动程度大。由式(2)计算得到的超声衰减系数与使用Image J软件测得的平均晶粒尺寸进行线性拟合,拟合效果如图5所示其线性拟合公式如下:

y=178.57α-0.74

(3)

式中,y为平均晶粒尺寸；α为衰减系数。

由式(3)可以得到通过激光超声衰减计算出的材料平均晶粒尺寸如表4所示。

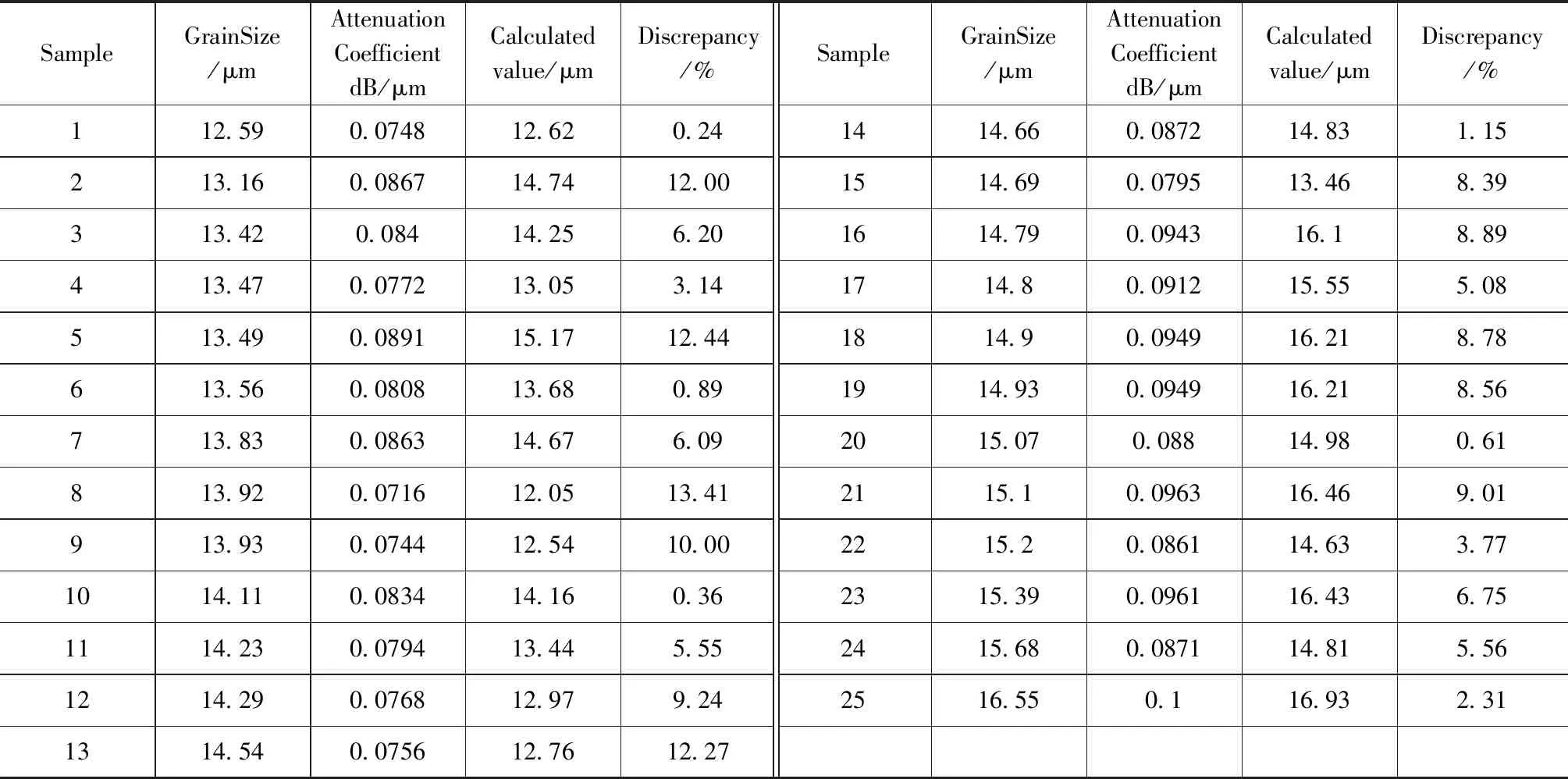
表4 幅值法平均晶粒尺寸预测Tab.4 Average grain size prediction by amplitude method

可见,所测试样的平均晶粒尺寸与所检测试样的平均晶粒尺寸误差较大,平均拟合偏离度为6.4 %,平均拟合误差值为0.92 μm,最大偏离度为13.41 %,拟合误差值为1.87 μm。 可见,直接采用幅值法进行晶粒尺寸的拟合存在较大的误差。

3.3 SVD法降噪后计算晶粒尺寸

在实际测量中,超声波信号受到设备稳定性、检测环境的变化和试样内部组织不均匀性等噪声的影响,并且激光超声检测中超声信号的采集经常含有大量低频噪声。本节提出一种通过奇异值分解的信号降噪方法来滤除超声信号中的噪声进而提高超声检测的精度的方法。奇异值分解基本思路是对观测信号进行相空间重构,利用SVD将观测信号空间分解为一系列奇异值对应的加噪信号子空间和噪声子空间,保留前面对应加噪信号子空间的若干个较大奇异值而其余奇异值全部置零,再利用SVD逆过程得到纯信号矩阵的估计式,最后由相空间反重构恢复出降噪后的信号。

本节中奇异值的选取采用频谱分析法[11]对超声信号进行快速傅里叶变换(Fast Fourier Transform,FFT),通过图6(a)频谱分析图确定其主频的个数n为6。由于有效秩的阶次p与源信号的主频个数n有确定的倍数关系,即p=2n,利用这种倍数关系可以确定有效秩的阶次p值为12,即取前12个较大的奇异值所对应的有用信号进行信号重构。对原始超声信号进行奇异值分解后再重构得到一维时间信号,其典型效果图如图6(b)所示。

对降噪后信号提取如图6(b)所示3P、5P、7P的波峰左右各600个点以得到第二次完整回波、第三次完整回波和第四次完整回波,对其各完整回波进行快速傅里叶变换(FFT),分析得到其频域振幅后使用振幅衰减法求其衰减,得到频域下超声衰减系数。

图6 奇异值分解降噪过程原理图Fig.6 Schematic diagram of singular value decomposition noise reduction process

由此计算得到的超声衰减系数与使用Image J软件测得的平均晶粒尺寸进行线性拟合,拟合效果如图7所示。

图7 奇异值分解降噪信号衰减系数与晶粒尺寸拟合图Fig.7 Singular value decomposition noise reduction signal attenuation coefficient and grain size fitting diagram

由图7可见,超声波的衰减随着晶粒尺寸的增大而增大,且拟合效果较好,拟合优度达到了91 %,其拟合误差值方差为0.25,拟合公式如下:

y=11.97α+9.136

(4)

式中,y为晶粒尺寸计算值；α为衰减系数。

由式(4)所计算出得平均晶粒尺寸如表5所示。将由幅值法(表4)与SVD降噪法(表5)所得的各样品晶粒尺寸计算偏离度进行对比分析如图8所示。

表5 SVD法平均晶粒尺寸预测Tab.5 Average grain size prediction by SVD method

图8 幅值法与奇异值分解法偏离度对比分析图Fig.8 Comparison analysis chart of discrepancy degree between amplitude method and singular value decomposition method

由图8可见,在预测精度方面,经SVD降噪后的拟合偏离度最大为7.21 %,而幅值法拟合偏离度为13.41 %,在预测精度稳定性方面,幅值法偏离度方差为0.041,而经SVD降噪后的偏离度方差为0.019。可见,与幅值法相比,SVD降噪后能够有效的提高平均晶粒尺寸的预测精度和稳定性。

然而,经SVD降噪后仍存在一些偏离度较大的样品,如3号、4号、5和6号样品(分别对应图9中No.3、No.4、No.5和No.6数据点),其平均晶粒尺寸分别为13.42 μm、13.47 μm、13.49 μm、13.56 μm,但其超声衰减系数则分别为0.3458 dB/μm、0.3186 dB/μm、0.3639 dB/μm、0.4056 dB/μm,衰减系数相差较大,造成拟合偏离度较大。

图9 超声衰减系数与平均晶粒尺寸拟合图Fig.9 Fitting diagram of ultrasonic attenuation coefficient and average grain size

图9(b)所示为3号、4号、5和6号样品晶粒尺寸分布图,可以看出,6号样品中,晶粒尺寸大于10 μm的晶粒数量占比为65.3 %,晶粒尺寸大于20 μm的晶粒数量占为21.8 %,均大于其他三个样品,从而使得其衰减系数也最大。4号样品中,晶粒尺寸小于15 μm的晶粒数量占比值最大,为29.0 %,从而使得其衰减系数也最小。同时,由表3中3～6号样品的不均匀性因子Z来看,4号样品不均匀性因子Z为8.5,6号样品不均匀性因子Z为6.21,而3号和5号样品不均匀性因子Z分别为7.10和7.66正好是两者的中间值,所以,当平均晶粒尺寸相当时,晶粒尺寸分布即晶粒尺寸不均匀性因子Z是影响拟合精度的主要原因。

4 结 论

(1)采用奇异值分解(SVD)降噪方法可对激光超声检测金属材料平均晶粒尺寸的信号进行优化处理,SVD降噪法可将超声衰减系数与平均晶粒尺寸的拟合偏离度提高至7.21 %,优于幅值法拟合偏离度13.41 %；同时,经SVD降噪后的拟合偏离度方差为0.019,优于幅值法拟合偏离度方差0.041,提高了平均晶粒尺寸预测精度的稳定性。

(2)当金属材料的平均晶粒尺寸差别较小时,基于激光超声的平均晶粒尺寸拟合精度和稳定性主要影响因素为晶粒尺寸分布即晶粒尺寸不均匀性因子Z。