裂流垂向分布实验研究

常承书，邹志利*，王彦，闫圣

( 1. 大连理工大学 海岸及近海工程国家重点实验室，辽宁 大连 116024)

1 引言

波浪向海岸传播过程中会发生破碎和产生波生流（沿岸流、裂流和海岸环流），若波高在沿岸方向是变化的，则水流会在波高较小区域汇集而形成向离岸方向流动的速度很高、宽度很窄的裂流[1]。由于裂流速度很大（可达2 m/s），所以可以携带很大的流体流量，这对近岸水体的交换[2]和污染物的输移扩散[3]、海岸泥沙输移和水底变形[4]以及海中游泳者的人身安全都有着重要影响。

目前关于裂流的研究大部分集中于裂流水深平均速度或者水面速度的测量[5-13]，前者多采用多普勒声学点式流速仪（ADV）测量距水底1/3处的速度[5-8]；后者是通过浮子示踪技术得到水面处速度矢量场（环流流场）[9-13]。裂流沿水深分布的测量结果还较少。Wind与Vreugdenhil[14]利用水池内的边墙使沿岸流偏转而产生离岸方向流动的裂流，通过3个垂向测点得到了垂向速度分布，但所得速度从水底到水面仅有很小的增加趋势。Drønen等[6]在水槽壁处设置了半个裂流槽，测量了裂流槽内外6个垂向断面的流速垂向分布，所得槽外裂流速度垂向变化较大，槽内速度变化很小。Haas和Svendsen[15]测量了对应无限长沙坝海岸的裂流槽中心线上7个断面上的速度垂向分布，指出在槽内速度垂向变化较小，但随着离岸距离的增大，这一变化逐渐增大。

裂流除上述由水底地形（沙坝和裂流槽）所导致的外，还包括边界导致的和交叉波浪场导致的，现有对边界所导致的裂流的研究集中于丁坝所导致的裂流流动。Pattiaratchi等[16]通过现场测量研究了丁坝区的裂流特征。Scott等[17]研究了现场单个丁坝和丁坝群引起的裂流场，得到丁坝反射区产生的裂流形态会受到沿岸流影响的结果。但有关的物理模型实验研究还未见到。

从上述研究可以看出，裂流三维分布的实验研究还不够充分，结果覆盖的情况有限，特别是对边界（丁坝）控制的裂流垂向分布还没有实验结果。本文给出了有关研究结果，所考虑的丁坝为全反射边界，所以也包含了交叉波浪场的影响，得到了沙坝海岸丁坝附近交叉波浪场产生裂流的三维分布的实验研究结果。文献[18]仅测量了此研究的部分实验结果，本研究通过增加波况、增加沿水深测量点和测量时间给出了完整的实验结果，在分析测量速度时变特征对结果的影响基础上，得到了较为全面的沿裂流速度剖面中心线的时均速度矢量沿水深的分布特征。

2 实验设置

2.1 实验地形

实验是在大连理工大学海岸及近海工程国家重点实验室的多功能水池进行的，水池长55 m，宽34 m，深0.7 m，实验波浪由70块造波板组成的推板式造波机生成。如图1所示，实验地形为含沙坝的坡度为1∶40的平坡海岸，在海岸的一侧面设置了长为25.7 m的丁坝，以形成反射波浪场。为了延长海岸线长度及形成斜向入射波浪，沙坝海岸模型与造波板夹角取为30°，坡脚距造波板的最近距离为9 m，静水线以上留有3 m的海岸长度以供波浪爬坡，在水域两侧设有不同长度的两个导浪墙。实验中水深在坡前平底处保持为0.45 m。沙坝剖面为高斯型剖面，宽度为2 m，中心线距静水线5 m，坝顶水深为0.045 m。在沙坝上距丁坝1.5 m处开有宽度1.0 m的裂流槽。坐标系原点取为丁坝与静水线的交点，x轴正向指向离岸方向，y轴正向指向离开丁坝方向，z轴垂直向上为正。

图1 实验地形和裂流槽布置Fig. 1 Experimental topography and rip channel

以上设置所形成的波浪在沿岸方向存在交替分布的驻波节腹点（图2），裂流槽中心线相对于这些节腹点的位置是随波浪周期不同而不同的：其在周期为1.0 s时与第2个腹点重合、在周期为1.5 s时接近第1个节点（右偏0.14 m）、在周期为2.0 s时位于第1个腹点与第1个节点之间（第1个节点位于裂流槽的左侧边缘）。在下面的讨论中将给出这些不同相对位置对裂流垂向分布的影响。

图2 实验波浪场照片（a）和沿节腹点波高测量结果（b）Fig. 2 Photo of experimental wave field (a) and the cross-shore wave height variation along node and anti-node lines (b)

2.2 波浪场及测量

海岸的波浪在丁坝反射后会形成交叉波浪场，即形成沿岸方向（y方向）的驻波。为研究这样的波浪场所形成的裂流的特征，实验中考虑了具有不同波高的3个周期（1.0 s、1.5 s、2.0 s）的规则波和不规则波，波高范围为2.73～5.91 cm，见表1。不规则波波谱取为JOWNSAP谱。这些波浪所对应的实际波浪可采用1∶16～1∶25的模型比尺换算得到，如采用1∶16比尺，对应的原型波高为0.44～0.95 m、周期为4.0～8.0 s，属于常浪情况下的波况。

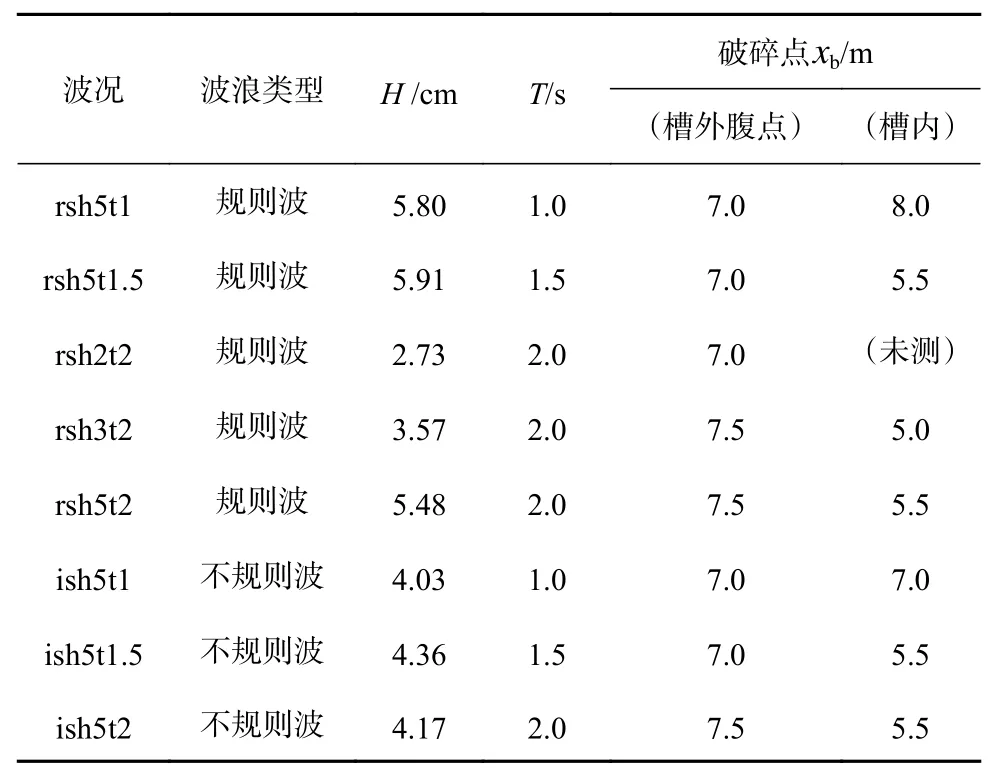
表1 实验波况Table 1 Test conditions

实验中产生的沿岸驻波的理论波长Ly=2π/(ksinα)（k为波数，α为波向）仅依赖于波浪周期，见表2。由于驻波节点处往往是裂流产生的位置，所以表中节点位置和个数是分析裂流特征的重要依据。裂流槽的存在也会决定裂流产生的位置，所以表中列出了裂流槽中心线相对于各驻波节点和驻波腹点的位置。

表2 叠加波浪的驻波波长、节腹点y坐标及相对裂流槽位置Table 2 The standing wavelength and y coordinates of node and anti-node points of superimposed wave and relative position of the channel

鉴于以上波浪场和裂流场的特征，实验中波高的测量是沿波浪节点和腹点进行的，由垂直海岸的3个测量架上的46个浪高仪同时进行，浪高仪间隔包括0.5 m、1 m、2 m和3 m（图1），测量的最大离岸距离为20 m。浪高仪采用北京水科院生产的电容式浪高仪，采样频率为50 Hz，采样长度为600 s。为了说明各节腹点波高沿垂直岸方向（x方向）的变化特征，图2b给出了规则波周期1.0 s、波高5.80 cm的测量结果。图中除了展示节腹点处波高存在的较大差异外，另一个在后面讨论裂流垂向分布拟合公式用到的结果是波浪破碎点的位置（见表1中波况rsh5t1）。因为波浪破碎前后采用的拟合公式是不同的，所以表1也给出了其他波况的波浪破碎点位置。

2.3 速度垂向分布测量

裂流速度垂向分布的测量是沿裂流水深平均速度剖面中心线进行的，其接近裂流槽中心线（在周期为1.0 s时与后者重合、在周期为1.5 s时右偏0.14 m、在周期为2.0 s左偏0.25 m）。测量由14个多普勒声学点式流速仪（ADV）进行，分别安置在两个测量架上（图3）。两个测量架同时进行速度测量，ADV垂向测量间隔为1～4 cm，具体依赖于测量处水深，测量点可由后面给出的垂向分布测量结果看出，共测量了水深范围从10 cm到20 cm的10个断面的速度分布。采样频率为50 Hz，采集时间对规则波一般为900 s，但为了考察裂流不稳定性所引起的速度长时间摆动，对有些波况测量时间延长为1 800 s（以使得时间序列至少包含3～5个长周期摆动）。对不规则波测量时间都取为1 800 s。

图3 流速仪垂向布置Fig. 3 Vertical layout of the acoustic droppler velocimeters

由于以上速度测量是定点测量，不能给出整个速度矢量场的分布特征，所以实验也采用了浮子示踪测量技术，通过跟踪浮子轨迹来得到水面上速度矢量空间分布[13]（图4）。

图4 浮子示踪得到的流场矢量与对应的涡量分布Fig. 4 The flow field vector and corresponding vorticity distribution obtained by float tracing

3 裂流三维分布特征

图5 给出了波况rsh5t1的速度垂向分布测量结果的速度矢量图及其x和y两方向的速度分量时均值（U,V）（在以下分别称为纵向速度和横向速度）的分布曲线。由图可以看出，沿裂流槽裂流流动的三维特征主要表现为两速度分量沿水深变化明显，特别是横向速度分量时均值V沿水深除大小变化外，还存在着符号的变化，这表明在各测量的垂线上，速度矢量由水面到水底存在着左右摆动，这一摆动在沿裂流流动方向（x方向）的各测量垂线上也存在很大不同和变化。这充分表现出了裂流流动三维分布的复杂特征，但由于在裂流槽内横向速度时均值与纵向速度时均值相比幅值较小（仅是后者的1/4），所以流动整体上仍然表现为沿裂流槽（x方向）的流向离岸方向的射流特征。

图5 裂流速度垂向分布矢量（波况rsh5t1，t=100～900 s）Fig. 5 Vertical distribution of rip current vertical vector (case rsh5t1, t=100-900 s)

除以上垂向分布特征外，裂流流动还存在着以下两个时变特点：一是存在着受时均驱动力控制的平均分量；二是存在着流动不稳定性导致的波动分量（参见文献[19]） ，所以可以将总的速度表达为：U=U+其中是时间平均的速度的定常部分，是速度的波动部分。作为例子，图6显示了波况rsh5t1的速度时间历程及其时均值图中结果也显示，流速在t=50 s左右时曲线的时间平均值趋近于更长时间的平均值，所以可以认为水流速度平均值在t=50 s之后已经达到稳定值。

图6 测量流速时间历程和时均值（波况rsh5t1）Fig. 6 Time series and time-average value of measured velocity (case rsh5t1)

式中，（sxx,sxy,syy）为三维时均辐射应力；为平均水平面升高；νe为流动涡粘系数；ρ，g分别为流体密度和重力加速度。当取涡粘系数νe为常数时，可以容易地由以上方程判断出沿水深的分布特征，这时可以对方程直接积分得到如下抛物线形式的解，即

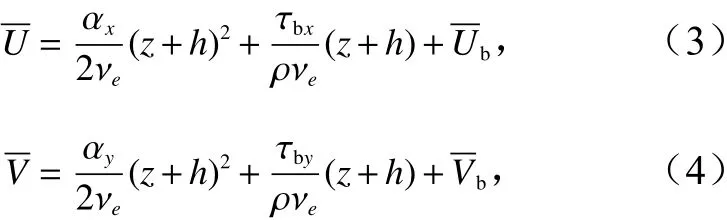
式中，h为静水水深；（τbx,τby） 为水底摩擦力；（Ub,Vb）为水底处速度；（αx,αy）为式（1）和式（2）的右端项。若考虑涡粘系数νe沿水深是变化的，则所得解可以为对数型分布或者幂函数型分布，下一节将针对纵向速度U给出对此的详细讨论。

图7 不同时间段裂流横向速度垂向分布Fig. 7 Vertical distribution of transverse velocity in different time periods

以上速度矢量存在向丁坝偏转的特征可以通过图4给出的利用浮子示踪测得的整体流场及对应涡量图解释，图中也给出了布置在距水底1/3水深处的ADV测量的速度矢量，这些速度矢量代表的是水深平均流速的分布，与浮子示踪测得的水面处流速会有所不同，二者同时给出可以对流场速度矢量有一个更全面的显示。图中，岸线位于x=0处，沙坝位于x=4.0 m～6.0 m处。由图可见，在裂流槽入口附近的x=4.0 m至岸线区域处，裂流槽两侧涡量强度是不对称的，这一不对称涡量分布主要是由丁坝对沿顺岸方向（y方向）流向裂流的补偿流的截断所导致，裂流的补偿流速度方向均为指向裂流槽方向，而靠近丁坝一侧的速度较小，所形成裂流补偿流也较小。这使得上层水体（浮子示踪仅能代表上层流体的速度）速度矢量在裂流槽内都向丁坝侧偏转（为负值），而在流出裂流槽后，上层流体速度矢量则偏向背离丁坝方向侧偏转（为正值）。这一上层流动显然会影响下层水体的流动，即影响速度垂向分布，但除此影响之外，正如式（1）和式（2）所示，还会受到涡粘系数νe垂向分布和三维辐射应力梯度垂向分布，以及平均水平面梯度的影响，所以下层水体速度的垂向分布表现得更为复杂，但在裂流槽内3个垂线x=4.5 m，5.0 m，5.5 m仍然表现出具有式（3）所示的抛物线型分布形态。而在裂流槽入口x=4.0 m和出口x=6.0 m，7.0 m处垂线垂向分布已经偏离这一分布形态。

4 纵向速度U垂向分布特征

由于横向速度的平均值受到环流流动的影响，具有随机性，无法给出其统一的分布特征，但纵向速度的随机性较小，可以给出其平均值的统一分布，因此这里详细讨论纵向速度U的垂向分布规律。

4.1 垂向分布规律

对其测量结果采用以下幂函数进行了拟合，

式中，＜U>为速度U水深平均值；m为常数。该拟合函数符合Barenblatt[21]提出的相似理论及不完全相似假定。以上拟合仅应用于波谷以下的速度，波谷以上的速度会受到水面波动导致的流速仪出水影响，为了消除出水部分对速度平均值的贡献，对波谷以上流速采用了以下分布[22]：

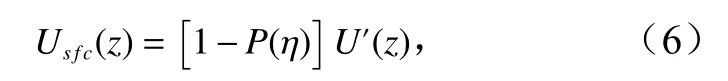
式中，U′(z) 对 应以上幂函数分布；η 为波面升高；P(η)为波面升高所遵循的高斯分布的累积概率，可由下式计算得出

研究中发现对破波带内（x＜xb）和破波带外（x≥xb），拟合函数（5）的指数需要选取不同的值：破波带内取m=1/7，破波点（x=xb）和破波带外取m=2，且该破碎点应当取为波浪场中最大破碎点，即裂流槽外波浪腹点的破碎点（表1）。由此可知，裂流纵向速度在破波带内服从通常湍流时均速度所遵从的1/7指数分布律，而在破波带外遵从类似于波浪正向入射海岸所形成的海底回流在破波带外的垂向分布规律[20]，二者都是由于破波带外湍流影响减小的缘故。以上两种分布都与式（3）中抛物线型分布是有所偏离的，这是因为在破波带内外涡粘系数νe事实上都不为常数：在破波带内若取νe为线性分布，则对应的是对数型分布，这实际上与以上幂函数型分布很接近。

为了验证不同波高情况（对应不同破碎点）以上速度分布规律的适用性，图8给出了同一周期T=2.0 s、3个不同波高情况的时均纵向速度的垂向分布测量结果及式（5）给出的垂向分布曲线。由表1知，这3个波况的波浪破碎点是不同的，两个较大波高波况（rsh3t2和rsh5t2）破碎点都为x=7.5 m，即图中所有剖面都位于破波带内；小波高波况（rsh2t2）破碎点为x=7.0 m，除x=7.0 m外图中其他剖面都位于破波带内，这些剖面的实验测量结果都与m=1/7的式（5）的结果接近。小波高情况的x=7.0 m剖面恰好位于破碎点，对应的实验结果与m=2的式（5）的结果接近。这些结果证明了以上所规定的式（5）的适用条件。

为了定量的描述以上拟合结果的精度，下面由以下均方根误差来给出式（5）与实验结果的拟合误差评估

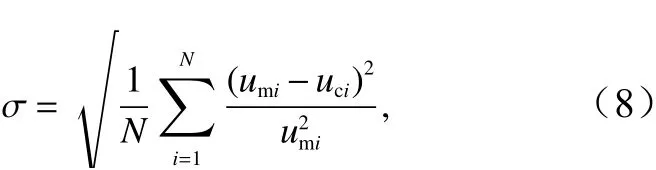
式中，N为波谷以下测点总数；i为测点数；umi为 第i个位置处的流速测量结果；uci为第i个位置处的流速拟合结果。计算中没有包含波谷以上和速度小于2.0 cm/s的测点，因为前者包含了流速仪出水影响，后者由于速度绝对值很小导致相对误差过大，会破坏整体的相对误差结果。对图8中所有曲线结果的计算表明，误差σ的平均值是9.8%，最大值是12.4%，后者发生在断面x=4.5 m、波高H=5.48 cm情况。

4.2 节腹点与裂流槽相对位置的影响

如2.1节所述，不同周期波浪的节腹点与裂流槽中心线的相对位置是不同的，为了研究这一不同的影响，图9给出了周期T=1.0 s、1.5 s和2.0 s时（rsh5t1、rsh5t1.5和rsh5t2）纵向速度时均值U的垂向分布及式（5）给出的分布曲线。其中取m=2的剖面分别对应x≥7 m、x≥7 m和x≥7.5 m。由图可见，不同周期波况的纵向速度也都服从上述在破波带内为指数1/7、在破波带外为指数2的幂函数分布。这表明，对不同的波浪节腹点与裂流槽相对位置，裂流纵向速度的垂向分布规律是相同的，都服从上述幂函数分布。为了定量的说明这一点，如上面对图8中的分析一样，这里也采用式（8）对该图的拟合误差进行了评估，所得误差σ的平均值是11.0%，最大值是12.4%。

图8 同周期（T=2.0 s）不同入射波高纵向流速垂向分布Fig. 8 Vertical distribution of longitudinal velocity in the same period (T=2.0 s) with different incident heights

图9 不同周期波况的裂流纵向速度垂向分布Fig. 9 Vertical distribution of longitudinal velocity in conditions with different periods

尽管有以上相同点，但3个波况的垂向分布还是存在着一些差别：裂流槽上游段（x=4.5～5.5 m）纵向速度时均值的幅值是随周期的变大而变大的；在裂流槽末端出口（x=6.0 m），三者差别也较明显，整个水深的速度幅值在周期1.5 s时要比其他两个周期的小50%左右，而后两者差别不大，这是由于这一位置的流动受到裂流对应的环流流动的影响较大，特别是速度矢量的方向。波浪周期不同，环流的水平尺度（半径）将不同，所以会直接影响裂流离开裂流槽的速度的大小和方向。

4.3 不规则波情况的结果

以上对于规则波情况的结果也适用于不规则波情况，即纵向速度存在着稳定的平均值且满足幂函数分布，横向速度存在着随不同时间段具有不同时均值的特征，并且由于波浪不规则性的影响，这一特征比规则波情况更为明显。为了说明以上纵向速度垂向分布的特征不随不同波浪节腹点相对裂流槽位置而变化，图10给出了周期T=1.5 s不规则波情况下纵向速度沿裂流水深平均速度剖面中心线的垂向分布，对破波带内的x＜7 m剖面取m=1/7，破波带外的其他剖面取m=2，其他两个周期结果也类似。这表明，式（5）的拟合函数仍然适用。

5 结论

本研究通过物理模型实验结果给出了沙坝海岸丁坝附近交叉波浪场形成的裂流的三维分布特征（沿裂流水深平均速度剖面中心线），讨论了波浪节腹点和裂流槽相对位置的影响以及规则波和不规则波情况结果的差异，为研究由丁坝所形成的边界控制的裂流提供了实验研究结果。这一结果对裂流引起的海岸悬移泥沙输移及其对应的海底变形具有实际应用价值，因为悬移质泥沙输沙率的确定依赖于水流速度的垂向分布。研究所得到的主要结论如下：

（1）裂流横向速度时均值会由于处理时间段不同而出现较大差异，但沿水深分布存在着共同的特征：裂流槽内裂流速度沿水深存在着偏向丁坝的分布，这是由于丁坝对沿岸流动（包括裂流的补偿流）的阻断作用所导致。

（2）裂流纵向速度的垂向分布呈现幂函数型，但破波带内指数为1/7，破波带外指数为2。这一结论对规则波和不规则波都适用，也不受波浪节腹点与裂流槽中心线相对位置不同（波浪周期不同）的影响。

（3）总的速度矢量三维特征。裂流速度矢量整体呈现出旋转射流的状态，表现为主流为离岸方向的纵向流，伴随着横向速度大小和方向变化引起的偏转。偏转特征是不同时间段平均速度都存在整体向丁坝方向偏转。