夹层玻璃强度等效厚度与应力计算方法研究
章 超 王福花 朱清淳 吴剑国
(1 .浙江工业大学 土木工程学院 杭州310023;2.中国船舶及海洋工程设计研究院 上海200011)
0 引 言
夹层玻璃是由两层或多层透明有机高分子材料与夹在中间的PVB(聚乙烯醇缩丁醛)、EVA(乙烯—醋酸乙烯共聚物)以及PU(聚氨酯)等材料制成的平面或曲面玻璃制品,因其具有良好的抗冲击性能、防碎片化脱落等特点,广泛应用于船舶驾驶室窗、舷窗。由于驾驶室窗、舷窗等区域的玻璃容易受海浪、风等作用而碎裂,导致海水浸湿设备、碎片划伤船员,影响船舶的航行与作业,ISSC对此颇为关注,拟开展对标研究。
在规范方面,BS ISO 11336-1-2012[1](简称BS)、ASTM E1300-12a[2](简称ASTM)、JGJ 102-2003(简称GB)[3]均有针对单层玻璃和夹层玻璃的相关分析、强度校核的公式和要求,并且BS ISO 11336-1-2012[1]第一部分的等效厚度理论分析中还考虑了夹层玻璃板层间的剪切传递,但是国内外规范之间的夹层玻璃等效厚度公式差异较大。马眷荣等[4]利用薄板小挠度弯曲理论,对两片等厚度玻璃制作成的夹层玻璃进行了理论研究,得到了夹层玻璃力学模型。庞世红等[5]研究了在均布载荷下夹层玻璃的抗弯性能与等效厚度,结果表明胶片厚度的增加不利于夹层玻璃抗弯性能的提高。Xu J和Li Y B[6]提出等效泊松比与等效弹性模量的概念,即将夹层玻璃板视为一个整体,以此来计算等效泊松比与整体等效弹性模量。在复合材料方面,李江涛等[7]和唐红艳等[8]介绍了复合材料在船舶上的应用现状与最新进展。
本文根据复合材料层合板经典弯曲理论,采用纳维尔解法推导出不计横向剪切变形影响的新夹层玻璃等效厚度公式,分别采用线性和非线性有限元方法,对在均布载荷作用下的等效玻璃板与夹层玻璃板进行验证与研究,同时探讨了在有限元计算中玻璃的复合材料板单元层数对计算结果的影响。
1 夹层玻璃的等效厚度公式
1.1 规范等效厚度
BS ISO 11336-1-2012[1]与ASTM E1300-12a[2]的等效厚度teq的计算公式如下:
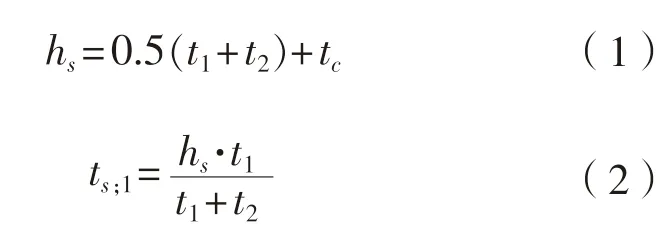
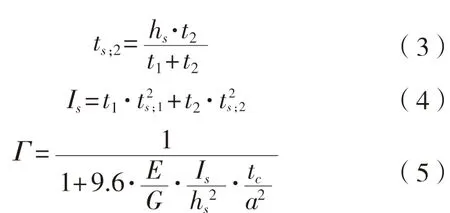
对于挠度的等效厚度:
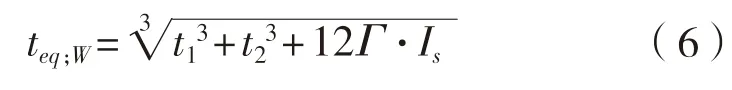
对于强度的等效厚度:
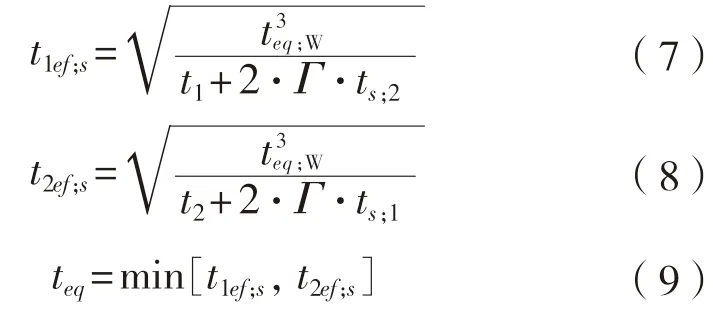
式中:t1为上层板厚度,mm;t2为下层板厚度,mm;tc为胶体厚度,mm;hs为夹层玻璃厚度,mm;Γ为剪切传递系数;Is为系数,mm3;、为分配系数,mm;为对于挠度的等效厚度,mm;teq为对于强度的等效厚度,mm。
JGJ 102-2003[3]夹层玻璃等效厚度teq的计算公式如下:

符号含义同上。
1.2 夹层玻璃板应力的理论值计算
夹层玻璃实物见图1。

图1 夹层玻璃板
将夹层玻璃板简化为四边简支,受均布载荷的均匀各向同性的线弹性层合板。夹层玻璃板的坐标为X向指向板的长边,Y向指向板的短边,Z向垂直向上,如下页图2所示。
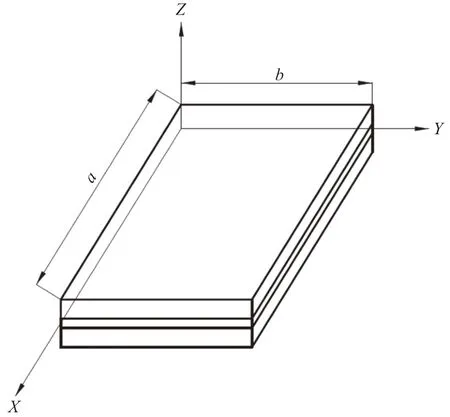
图2 夹层玻璃坐标系示意图
根据《复合材料结构的力学性能》[9]中的复合材料层合板经典弯曲理论可知,不计横向剪切变形的影响,采用纳维尔解法得出位移函数,从而求出夹层玻璃应力,具体过程如下:
层合板的弯曲方程为:

式中:ω为层合板挠度,mm; 为横向载荷,N/mm2;D11、D12、D22、D66分别为层合板刚度矩阵中对应的值。
将位移函数 展开为三角级数的形式:

式中:a、b分别为夹层玻璃板的长度和宽度,mm;Amn为待定系数;m、n为系数。
在求得位移函数 之后进一步得出板中应力、应变。板中的任一点处的应力可由下式求得:
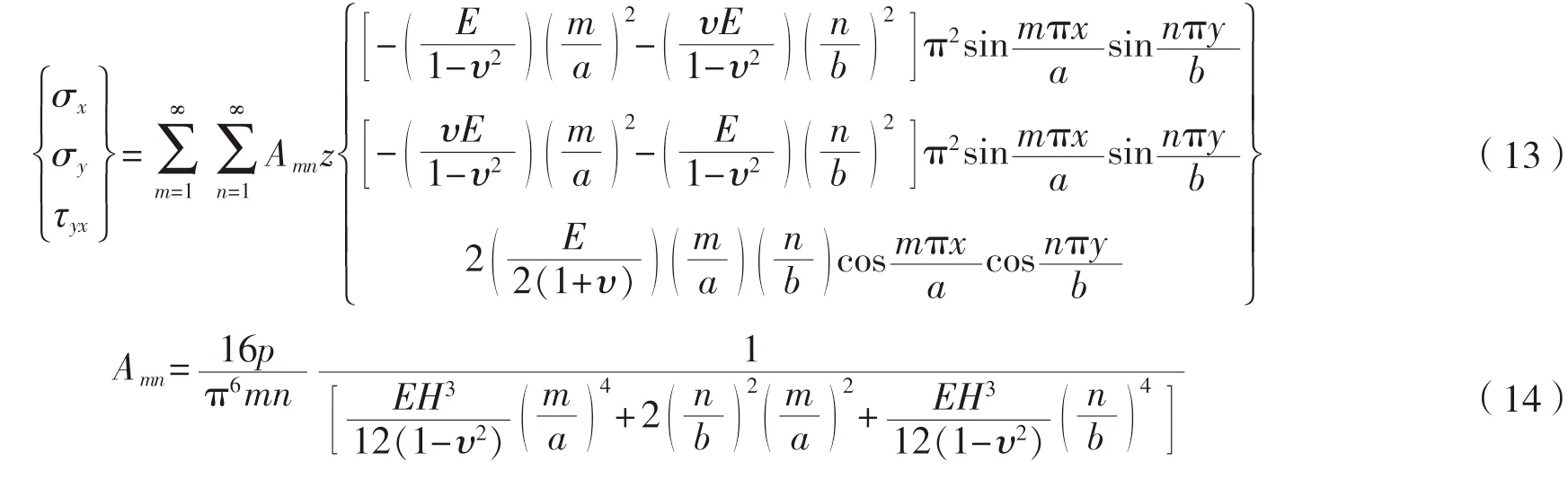
式中:z为所选点到中面的距离,mm;H为夹层玻璃的总厚度,mm;υ为夹层玻璃的泊松比;E为弹性模量,MPa;其他符号含义见式(12)。
1.3 新等效厚度公式推导
将夹层玻璃板简化为四边简支,受均布载荷厚度为teq的各向同性线弹性矩形板。等效的原则为将等效板与夹层板长边中点的正应力相等,即公式(15)与应力公式(13)中的σy相等,求得等效厚度计算公式如下:


式中:p为均布载荷,N/mm2;k3为与夹层板的长宽比有关的系数,部分取值见表1,详见《船舶结构力学手册》[10];其他符号同式(13)。
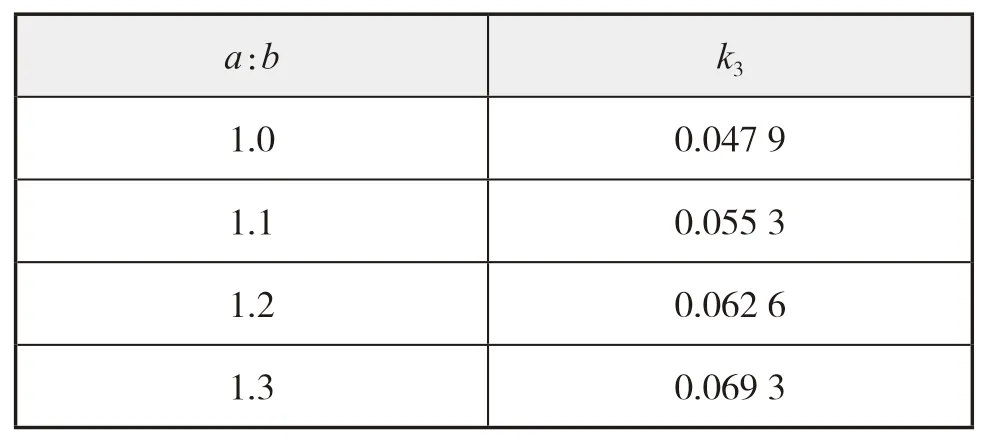
表1 k3的取值
一般应力求解,取m=3,n=3即可。本文为简单起见,取m=1,n=1得到算例的新等效厚度公式为:

2 玻璃板应力的理论值计算
2.1 夹层玻璃的力学参数
以 受 横 向 均 布 载 荷pD= 0.013 78 N/mm2,长2 m、宽1 m的三层夹层玻璃为例,其上下层玻璃的厚度分别为t1=t2= 8 mm,中间层PVB的厚度为h=1.52 mm,如图3所示。

图3 三层PVB夹层玻璃板构成示意图
玻璃与常温20℃下的PVB的材料参数如表2所示。

表2 材料属性表
2.2 夹层玻璃板应力的理论计算
按照上述方法,针对2.1节中夹层玻璃的力学参数,各规范与新推导的等效厚度公式计算结果汇总如表3所示。根据《船舶结构力学手册》[10]第一章第二部分中的理论,以及规范BS ISO 11336-1-2012[1]和JGJ 102-2003[3]中的等效厚度公式得到的等效厚度,进行等效单层玻璃板的应力理论计算。根据公式(13)计算夹层玻璃板应力理论值、等效单层玻璃板应力计算值与夹层玻璃板应力理论值如表4所示。
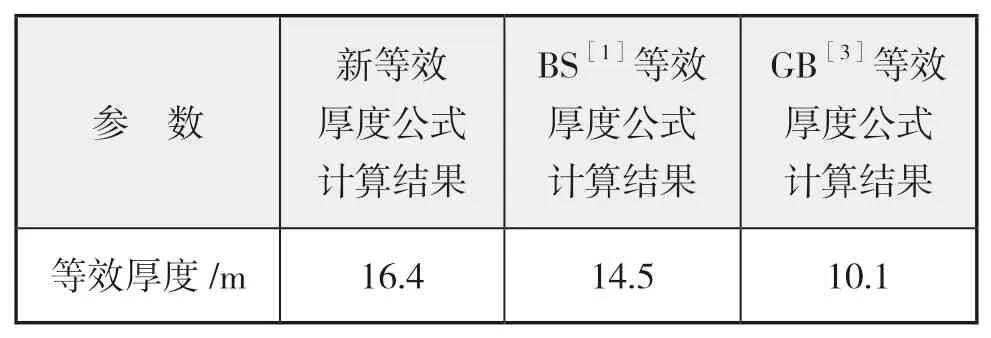
表3 等效厚度汇总

表4 应力比较
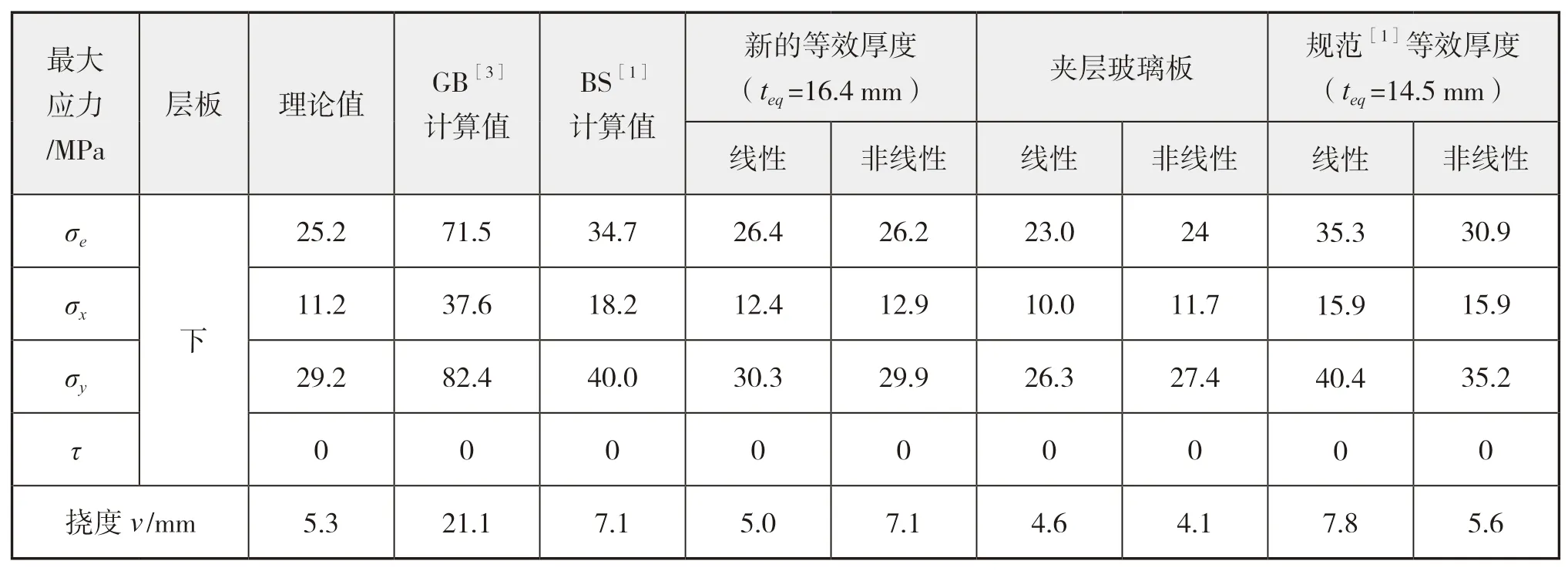
续表4
2.3 有限元计算
针对上述算例,采用Abaqus软件,分别创建等效单层玻璃板与夹层玻璃板有限元模型。计算模型采用弹性应力-应变关系。等效单层玻璃板的单元类型采用三维四结点薄壳单元(s4r),夹层玻璃板的单元类型采用复合材料板单元,均将网格划分为8 mm×8 mm,有限元模型和坐标系如图4所示。

图4 有限元模型示意图
边界条件为将板的A边设定为约束X、Z方向移动,C边设定为约束Z方向的移动,B边设定为约束Z方向移动,D边设定为约束Y、Z方向的移动,其中将夹层玻璃板中玻璃的复合单元划分为1层、5层、10层和30层。
由于夹层玻璃板中的中间层PVB具有材料非线性的特性,常温下胶片的应力-应变关系曲线如图5所示,所以对夹层玻璃板进行计算时分别进行线性与非线性计算。

图5 常温下胶片的应力-应变关系曲线
2.4 计算结果对比分析
不同等效厚度的单层与夹层玻璃板的线性与非线性有限元数值解对比见表4。等效厚度为teq=14.5 mm的等效单层玻璃板下,表面应力分布如下页图6所示。夹层玻璃板中的玻璃不同层数复合材料板单元计算结果汇总如下页表5所示。复合材料板单元层数为10层的夹层玻璃板下层玻璃应力分布如下页图7所示。
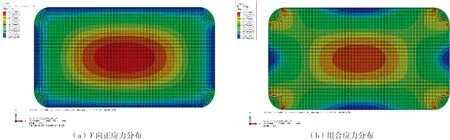
图7 夹层玻璃板应力分布图(复合材料板单元层数为10层)

表5 均布荷载作用下夹层玻璃的计算结果汇总
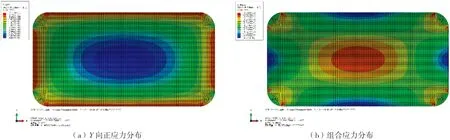
图6 等效单层玻璃板应力分布图
由表4可知,新推导等效厚度的单层玻璃板有限元模拟得到的数值与理论值较为接近,线性有限元分析结果与理论值结果偏差在4%之内,非线性有限元分析结果与理论值结果偏差在2%之内,线性计算结果比非线性计算结果大9%。由于线性计算结果相对保守,非线性计算更复杂、耗时长,所以在有限元计算时建议采用线性计算即可。由规范[1]计算求得等效厚度的非线性有限元分析结果相较于新推导的等效厚度非线性有限元分析结果大,所以在误差允许的范围内,新推导的等效厚度公式是准确的。由上页表5可知,复合材料板单元计算值随着复合材料板单元层数的增加,精度相应提高,但复合材料单元层数过多并无意义,建议以10层为宜。
3 结 论
本文通过研究分析得到以下结论:
(1)与规范[1,3]的等效厚度相比,本文新推导的玻璃夹层等效厚度公式具有更高精度;
(2)在进行有限元计算时,建议采用线性计算;
(3)鉴于玻璃板属于脆性材料,且正应力大于合成应力,所以建议按正应力进行强度校核;
(4)采用复合材料板单元进行玻璃应力计算时,随着玻璃分层数目增加,精度也相应提高,但玻璃层数过多并无意义,建议以10层为宜。

