混凝土抗拉与抗压强度尺寸效应统计模型

王志斌杨立云钱桂安李芹涛徐辉东

1. 中国矿业大学(北京)力学与建筑工程学院,北京 100083;

2. 中国科学院力学研究所非线性力学国家重点实验室,北京 100190;

3. 中国黄金集团有限公司莱州汇金矿业投资有限公司,山东莱州 261400;

4. 中煤矿山建设集团有限公司,安徽合肥 230000

尺寸效应是指材料的力学性能随几何尺寸发生变化,破坏时的强度值不再是一个材料常数[1]。大量研究表明,混凝土力学性能与试件几何尺寸密切相关[2-4]。在实际工程中,混凝土结构的尺寸通常较大,因试验条件和技术水平的限制,难以进行全尺寸结构模型试验,只能进行缩尺模拟,且样本数量有限,因此确定混凝土构件缩尺模拟结果的适用性至关重要。由于混凝土内部存在大量裂隙、孔洞及微细观上的非均质性,试验测得混凝土强度的离散性很大,尺寸效应也更加明显。

许多学者对混凝土抗拉和抗压强度尺寸效应进行了大量研究。Bažant 等[5]采用高度相同、直径不同的混凝土圆柱体开展劈裂试验,并根据Bažant 尺寸效应建立了混凝土劈裂抗拉强度与直径的关系,试验表明劈裂强度有随直径的增加先减小后增大的变化趋势。钱觉时等[6]分别对不同边长的高强混凝土试样进行弯拉强度测试,得出了高强混凝土弯拉强度的尺寸效应规律。安明喆等[7]对3 种不同尺寸的活性粉末混凝土(RPC)进行了弯拉强度试验,结果显示RPC 的抗弯强度具有明显的尺寸效应现象。张军等[8]对4 种自密实混凝土进行尺寸效应试验,研究发现随着试件尺寸提高,混凝土抗压强度均逐步降低。以上研究虽然在一定程度上得出了尺寸与强度之间的关系,但在分析混凝土尺寸效应时没有考虑强度的离散性。而混凝土作为一种典型的准脆性材料具有强度离散性和尺寸效应2 个显著特征。混凝土强度离散性是由岩石内部微观缺陷的随机分布造成的。从概率统计出发,尺寸效应也与缺陷的随机分布有关。混凝土结构尺寸越小,包含微观缺陷的概率就越小,对应岩石破坏时的强度越高;反之,混凝土结构尺寸越大,混凝土内部包含的微观缺陷越多,其破坏时的强度越低。因此,采用统计方法来评价岩石强度尺寸效应是十分必要的。

近年来Lei 等[9-12]提出的广义最弱链公式为评价混凝土等准脆性材料的尺寸效应提供了强有力的手段。该方法不仅可以解释强度的随机变化,而且在给定失效概率条件下,通过测试有限数量的小尺寸试件强度可以预测大尺寸试件强度,具有重要的工程价值。

本文将介绍Lei 提出的广义最弱链理论,并在Lei 研究的基础上,结合3 个案例中的试验数据,研究巴西劈裂法、四点弯法和单轴压缩3 种加载方式下,混凝土材料的劈裂抗拉强度、弯拉强度和抗压强度与试件尺寸之间的关系,建立相应的尺寸效应统计模型。

1 尺寸效应统计方法

1.1 最弱链理论

最弱链理论是Lei 提出的尺寸效应统计方法的基础。该理论认为,结构是由若干体积或面积的单元串联而成(图1),单元与单元之间是相互独立的。只有当所有这些单元都完整时结构才不会失效;反之,任意单元的失效将导致整个结构失效。由最弱链理论可知,材料破坏时强度的离散性本质上应符合一定的统计规律。

图1 串联结构示意图Fig.1 Tandem structure diagram

1.2 尺寸效应统计方法

材料中缺陷的空间分布直接影响脆性断裂的累积失效概率,以最弱链理论为基础,Lei 提出了在缺陷服从泊松分布或均匀分布假设下材料广义最弱链统计公式[9]:

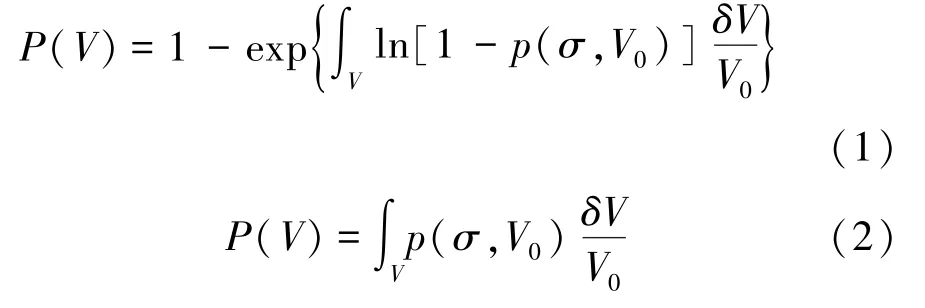
其中,V为断裂过程区体积;p(σ,V0)为材料内部某一个微单元发生破坏的概率;σ为微单元所受的拉应力;V0为一个缺陷所占的平均体积。

V的大小主要与材料破坏时服从的破坏准则有关。例如,在最大拉应力准则下,断裂过程区的体积为拉伸应力大于0 的区域(σ1＞0)。

由格里菲斯理论[13]可知,断裂临界应力与缺陷长度存在如下关系:

式中,ac为临界缺陷长度;k为阻止缺陷发生扩展的系数,与材料特性有关。

显然,p(σ,V0)取决于微缺陷尺寸a或应力σ,V0破坏的概率可表示为

式中,ac(σ1)为应力值为σ1条件下引发缺陷扩展的临界缺陷尺寸;amax为应力达到引发断裂的门槛值σth时缺陷发生扩展的最大尺寸。

这里以缺陷分布形式服从均匀分布为例,阐述Lei 提出的累计失效概率的推导过程[11-12]。设代表一个缺陷所占的平均体积为V0,在缺陷分布为均匀分布下,微元体δV含有缺陷的数量为δV/V0。令微元体失效的概率为δP,由最弱链理论可知,微元体不发生破坏的概率为[11]

材料全尺寸不发生破坏的概率为[11]

式中,p(σi,V0)≠1,当N→∞时,式(6)可写成式(1)。将V0失效概率使用3 参数的Weibull 分布表示为[12]

式中,m为形状参数;σ0为尺度参数;m和σ0只与材料性质有关。

当σth=0 时,将式(7)代入式(1),则在假设材料内部缺陷均匀分布下,全尺寸失效概率为[14]

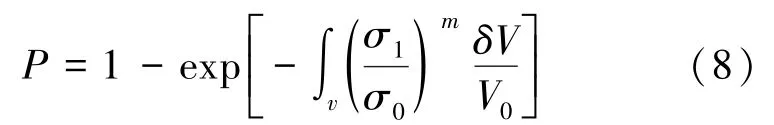
根据2 种缺陷分布所对应的累计失效概率进一步分析:结合式(7),令σth=0,由第一积分中值定理,式(1)和式(2)可改写为[14]

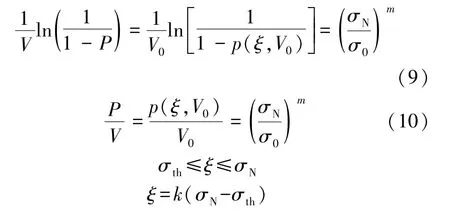
式中,ξ为一个应力值;k为一个常数(0 ＜k≤1);σN为发生破坏时的名义强度。

由式(9)和式(10)可以看出,等式的左边与材料内部缺陷的分布形式有关,等式的右边只与名义强度有关,这为建立尺寸与名义强度之间的关系提供了一种方法(图2),即尺寸效应统计方法。

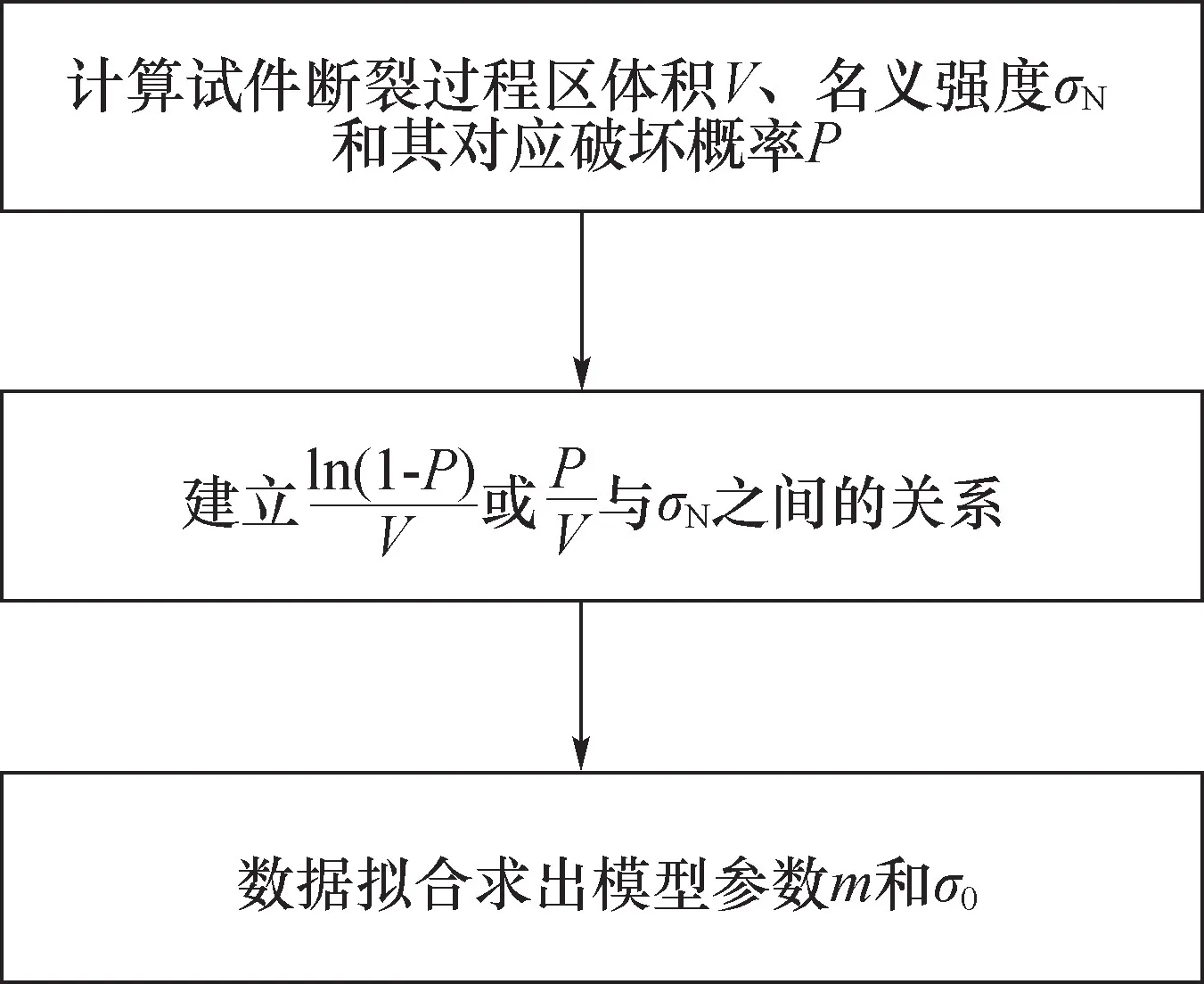
图2 尺寸效应统计方法Fig.2 Statistical method of size effect

2 案例分析

2.1 巴西劈裂法加载下混凝土抗拉强度与尺寸关系

Kanos 等[15]进行了3 种尺寸混凝土巴西圆盘劈裂试验,研究了混凝土劈裂抗拉强度与尺寸的关系,试件尺寸和每个试件对应的劈裂强度见表1,所测得名义强度为

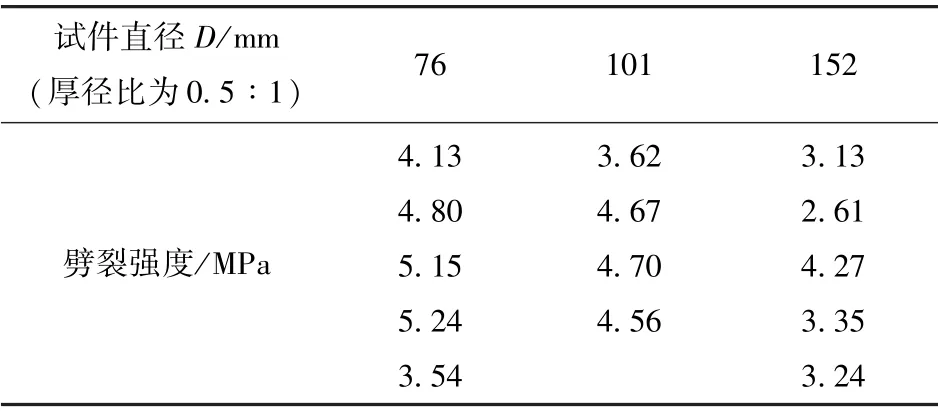
表1 试件尺寸及试件劈裂强度Tab.1 Specimen size and tensile splitting strength results obtained

式中,F为施加的荷载;D为圆盘直径;B为圆盘厚度。

混凝土在劈裂加载方式下的破坏主要受拉应力控制,其破坏服从最大拉应力准则,因此认为其可能发生破坏的区域为断裂过程区,即最大主应力大于零的区域。对圆盘试件在劈裂加载方式下应力状态进行数值模拟(选取直径76 mm 试件所测结果:弹性模量E=38.4 GPa,泊松比μ=0.119),从应力云图(图3)中可以看出,劈裂加载方式下断裂过程区的体积V接近于全体积。

图3 弹性力学第一主应力云图Fig.3 Stess contour in split loading mode

每组试件破坏时的强度所对应的累计失效概率由式(12)计算[10],计算结果如图4 所示。σi为每一组n个强度值由小到大排列的第i个强度值,该案例中n分别为5、4、5。

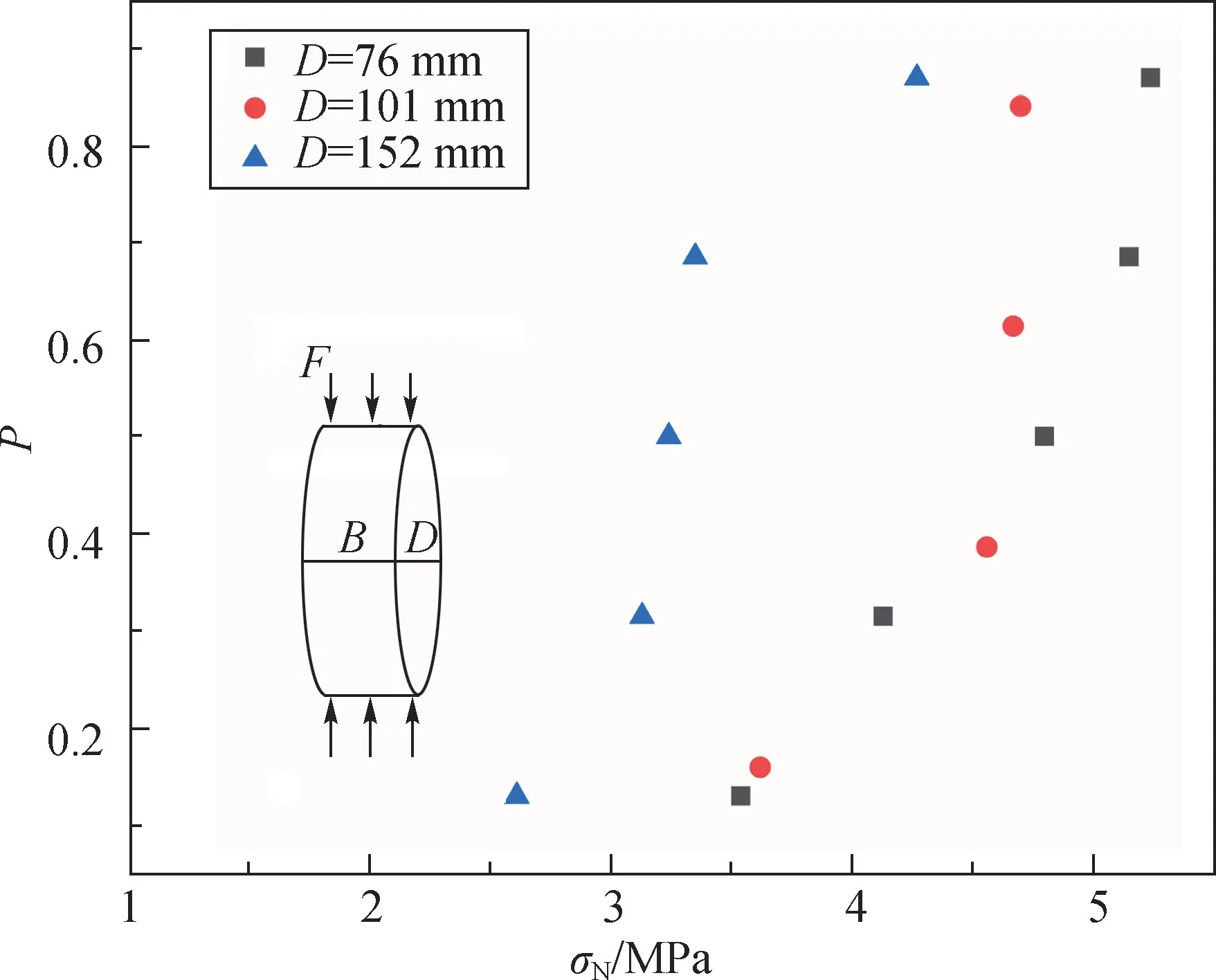
图4 圆盘劈裂强度经验概率Fig.4 Empirical Probability of Disc Splitting Strength

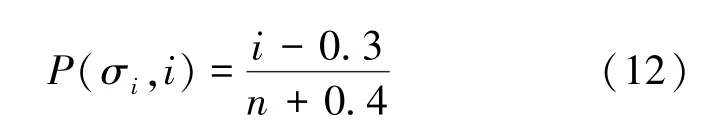
假设混凝土内部缺陷分布形式服从均匀分布或泊松分布,将图4 中数据转化为式(9)、式(10)的函数关系。从2 种分布假设下的拟合结果(图5)中可以看出,不同尺寸的圆盘试件所测得名义强度的对数值(lnσN)与失效概率和尺寸的复合参数和之间存在线性关系。在缺陷均匀分布假设下,线性拟合m=5.89,·V0=e21.68MPa·mm3,决定系数R2=0.90;在缺陷泊松分布假设下,线性拟合m=5.09,·V0=e20.96MPa·mm3,决定系数R2=0.89。2 种分布形式下R2值均大于0.8,拟合情况较好。因此,在该案例中,假设混凝土缺陷服从均匀分布或泊松分布,圆盘劈裂强度与尺寸的关系分别为

图5 2 种缺陷分布下的拟合结果Fig.5 The assumed fitting results under two defect distributions

2.2 四点弯加载下RPC 的抗折强度与尺寸关系

张立军[16]使用3 种不同尺寸的活性粉末混凝土(RPC 混凝土)进行抗折试验,研究尺寸对RPC混凝土弯拉强度的影响。该试验样本总计81 个(12 组50 mm×50 mm×200 mm、12 组100 mm×100 mm×400 mm 和3 组150 mm×150 mm×600 mm,每组3 个试件),所有样本均采用相同的配合比及养护条件。每个试件弯拉强度和累计失效概率关系如图6 所示。

图6 抗折强度经验概率Fig.6 Empirical probability of flexural strength

在四点弯加载方式下,试件破坏受拉应力控制,发生弯曲破坏时所测强度为抗折强度或弯拉强度,材料破坏依然服从最大拉应力准则。因此,该种加载方式下,断裂区体积采用纯弯段受拉区体积[14],即V=0.5h3,计算结果见表3。图7 为2 种缺陷形式下的拟合结果。

表3 RPC 试样尺寸Tab.3 Size of RPC specimens

图7 2 种缺陷分布下的拟合结果Fig.7 The assumed fitting results under two defect distributions

从图7 可以看出,缺陷均匀分布下模型参数m=12.97,·V0=e52.43MPa·mm3,相关系数R2=0.92,数据基本拟合在一条直线;缺陷泊松分布假设下模型参数m=10.97,·V0=e46.75MPa·mm3,R2=0.83,数据拟合较分散。基于缺陷均匀分布或泊松分布下的RPC 混凝土弯拉强度与尺寸的关系可由式(15)或式(16)表示,但对比2 种缺陷分布假设下的拟合效果,均匀分布假设更符合RPC 混凝土内部缺陷分布的真实情况。

2.3 混凝土抗压强度尺寸效应统计模型

陈宝春等[17]为研究超高性能混凝土抗压强度尺寸效应,分别对立方体和圆柱体共6 种尺寸的试件开展抗压强度试验,每种规格有12 个试件(3 种立方体试件边长分别为150 mm、100 mm 和70.7 mm,3 种圆柱体直径分别为70 mm、100 mm 和150 mm)。试验获得强度值和累计失效概率关系如图8 所示。本案例中的超高性能混凝土也是一种活性粉末混凝土,本文仅对材料内部缺陷服从均匀分布假设下分析。由于混凝土受压破坏机理较为复杂,为了简化分析,这里认为其破坏受拉行为控制,破坏准则依然采用最大主应力准则。

图8 经验概率Fig.8 Empirical probability

采用同案例1、2 相同的方法对立方体和圆柱体抗压强度数据分别进行线性拟合,如图9 所示。从图9(a)中可以得出,立方体试块抗压强度尺寸效应统计模型中,m=26.2,·V0=e151.15MPa·mm3,决定系数R2=0.87。从图9(b)中可以得出,圆柱体试块抗压强度尺寸效应统计模型中,m= 29.2,·V0=e166.4MPa·mm3,决定系数R2=0.89。2种形状所测抗压强度数据也拟合在一条直线上。该案例中,立方体和圆柱体2 种形状RPC 抗压强度与尺寸的关系可分别由式(17)和式(18)表示。

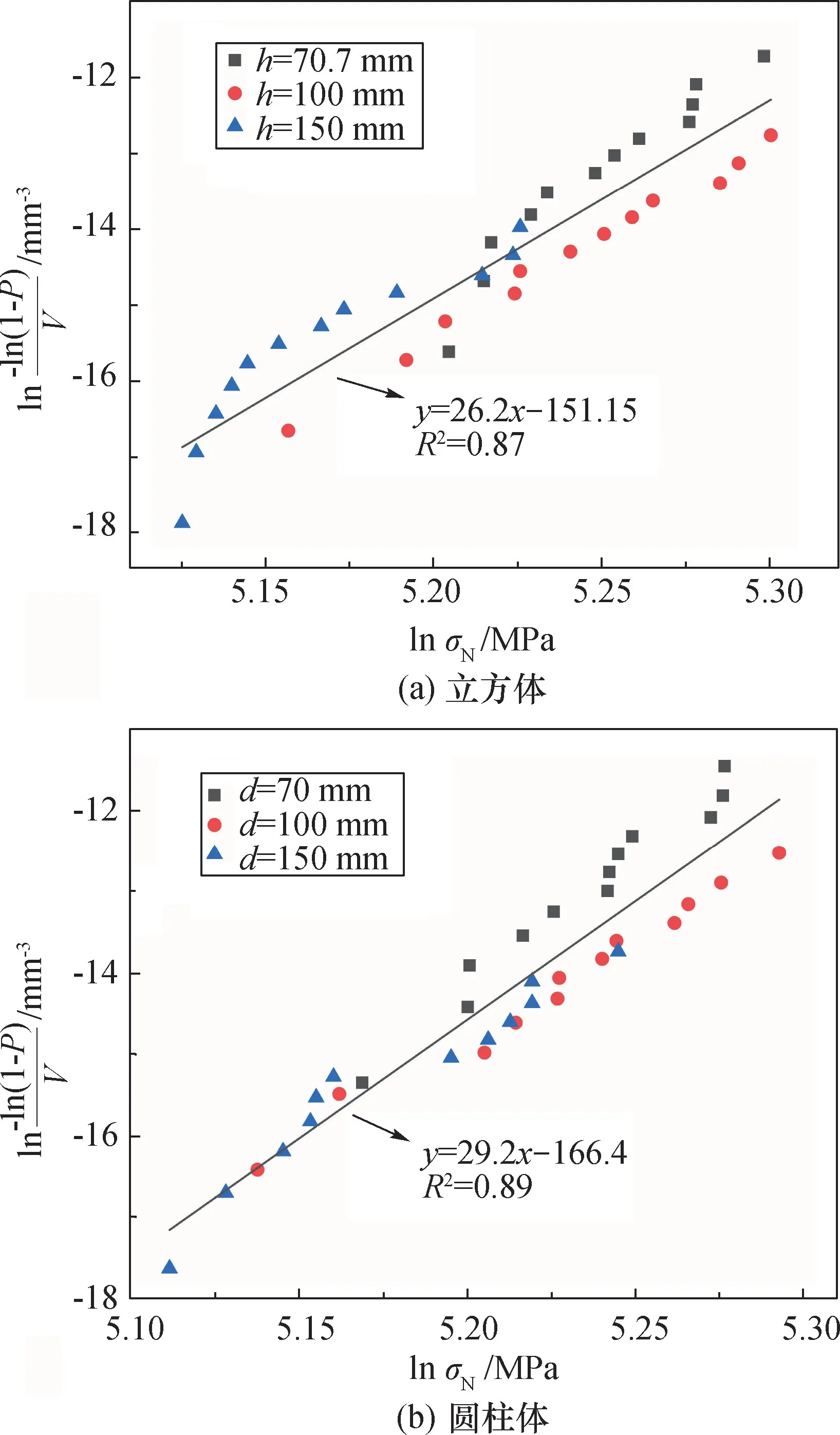
图9 2 种形状的尺寸效应拟合结果Fig.9 Fitting results of two shapes of size effect

3 结 论

根据广义最弱链公式所建立的尺寸效应统计方法适用于混凝土材料抗拉和抗压强度的尺寸效应分析;建立的模型还能同时考虑混凝土强度的离散性,实现了给定失效概率下混凝土不同尺寸试件强度的预测。

(1) 在普通混凝土劈裂抗拉强度尺寸效应统计分析中,2 种分布情况下的拟合结果差别不大。缺陷均匀分布情况下得到的结果略好,但由于分析所用的数据量较少,所以结果离散性稍明显,存在一定的误差。

(2) 对RPC 抗拉强度数据的分析结果表明,缺陷均匀分布下尺寸效应分析结果更优于泊松分布。均匀分布假设下所建立的尺寸效应统计模型可以很好地反映出RPC 弯拉强度与尺寸的关系。同时,该方法进一步反映出RPC 材料内部分布形式更接近均匀分布。

(3) 假设缺陷服从均匀分布,RPC 抗压强度与尺寸的关系也可以采用尺寸效应统计模型来描述。