基于CFD的空调室外交流风机工作点预测研究

曹锋

珠海格力电器股份有限公司 广东珠海 519000

1 引言

由于全球面临能源危机，提高能效已成为包括空调行业在内的各行业提高产品竞争力的主要手段之一。风机作为空调的关键核心部件，其效率直接影响空调整机能效，因此提高风机效率已成为提高空调整机能效的关键手段。由于风机由风叶与电机组合而成，其效率亦由电机效率及风叶效率共同决定。目前关于风叶仿真优化提高性能的研究颇多，文献[1][2]通过CFD仿真手段改变轴流风叶的内流特性进行风叶优化；Huang&Gau[3]应用反设计方法对风叶的三维叶型进行优化；黄愉太等[4]采用fluent对轴流风叶不同周向截面安装角进行流场分析，得到在最佳周向截面安装角时的优化风叶，效率提高3.42%；王嘉冰等[5]采用CFD分析了轴流风叶叶顶流场中叶尖涡的产生和发展轨迹，为风扇效率的提高提供了指导。但是实际工程应用中仍然存在即使风叶效率得到提高，风机总效率依旧得不到显著提高的现象，因此提前预测风叶与交流电机匹配时工作点的数据对于风叶设计及风叶选型就显得比较重要，但是目前关于此类的研究却非常少。缺少此类指导可能会导致风叶设计加工后匹配电机时出现偏离预期目标的问题，乃至需要返工设计，将在极大程度上延误产品开发进度。

本文基于某室外机壳体采用CFD对三款风叶进行非定常求解计算并且采用实验结果进行可靠性验证，同时结合交流电机特性曲线及空调室外机风道阻力曲线对风机的工作点参数进行有效预测，有助于预先评估空调风机性能进而指导风叶设计及选型，缩短产品开发周期及节约实验资源。

2 数值模拟及可靠性验证

2.1 数值模拟

数值模拟的几何模型与实际模型的一致性直接影响到计算结果的准确性，因此在对室外机风道进行建模时尽可能少的对模型进行简化，以保证仿真模型与实验模型的一致性。

整个计算域的模型以及室外机模型分别见图1、图2。考虑到室外机风道几何结构的复杂性，特将整个计算域划分为四部分，分别是：冷凝器前、冷凝器后、旋转体部分、冷凝器部分。由于需采用多孔介质模型来处理由冷凝器产生的压力损失，网格绘制时对冷凝器流体计算区域采用六面体网格处理，其余则采用四面体网格处理。

图1 流体计算域

图2 室外机风道（不含风叶）

为了提高计算精度，将计算分为两阶段稳态计算、非稳态计算。两者皆采用三维Navier-Stokes方程，湍流模型选取k-εRealizable两方程模型。计算方法均为SEGREGATED隐式方法。湍流动能、湍流耗散项、动量方程均采用二阶迎风格式离散；压力-速度耦合采用SIMPLE算法；近壁面处理采用非平衡壁面函数。进出口边界分别设置为压力进口、压力出口边界条件，采用滑移网格技术对风叶旋转流域进行处理，非定常计算采用每个时间步长风叶旋转3°进行迭代求解。

2.2 数值模拟可靠性验证

CFD计算结果精度直接影响预测结果的准确性，采用风机外特性实验室测得的实验数据对CFD计算结果进行验证。实验中工作电压为220 V，机外静压值为0 Pa，选用3种不同结构的轴流风叶进行相关研究，为便于描述分别将其命名为：风叶A、风叶B及风叶C，见图3。风叶的计算结果与实验结果对比见图4。

图3 风叶模型

图4 风量仿真结果与实验结果对比

为了便于评估仿真与实验测试偏差，定义任一款风叶的研究数据总量数量为n，任一数据点序号为i，在不同的工作转速N，任一款风叶风量的仿真结果Qs与实验结果Qe的平均偏差，见式（1），依次为0.45%、0.63%及1.04%。

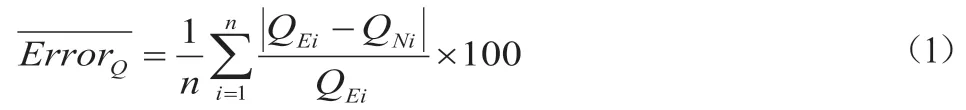
由力矩平衡方程可知：在风机运转时，来流气体施加在风叶上的力矩与风叶施加在电机轴上的力矩相等。因此采用电机力矩的测量值τE代表风叶的真实力矩来验证计算力矩τS的准确性，对比结果见表1。计算结果与实验结果的偏差Error计算方式见式（2）：

对比结果如表1所示，从表1可知：计算力矩τS与实验测试力矩τE的最大偏差仅仅1.44%，小于工程允许误差5%。因此基于CFD方法得到的风量-转速特性曲线及扭矩-转速特性曲线是可靠的。

表1 不同风叶扭矩计算结果与测试结果对比

3 交流风机工作点参数预测

交流风机的实际运行转速随着风叶负载的变化而变化，不同的风叶在同一室外机壳体中工作其工作转速大多是不同的。系统设计人员通常按照系统换热需求并且结合电机转速提出转速、风量需求，风机设计员根据设计转速、设计流量进行叶型设计。然而测试结果显示：风叶通常不能按照设计转速在空调壳体里面工作。这主要由于风叶在设计工作转速所对应的力矩与电机的力矩不等，导致风机不能按照设计转速在空调室外机风道中工作，因此在叶型设计时应考虑风叶力矩。

鉴于上述表达，基于CFD数值解析结果来对交流风机在室外机中工作点的预测流程如图5所示。

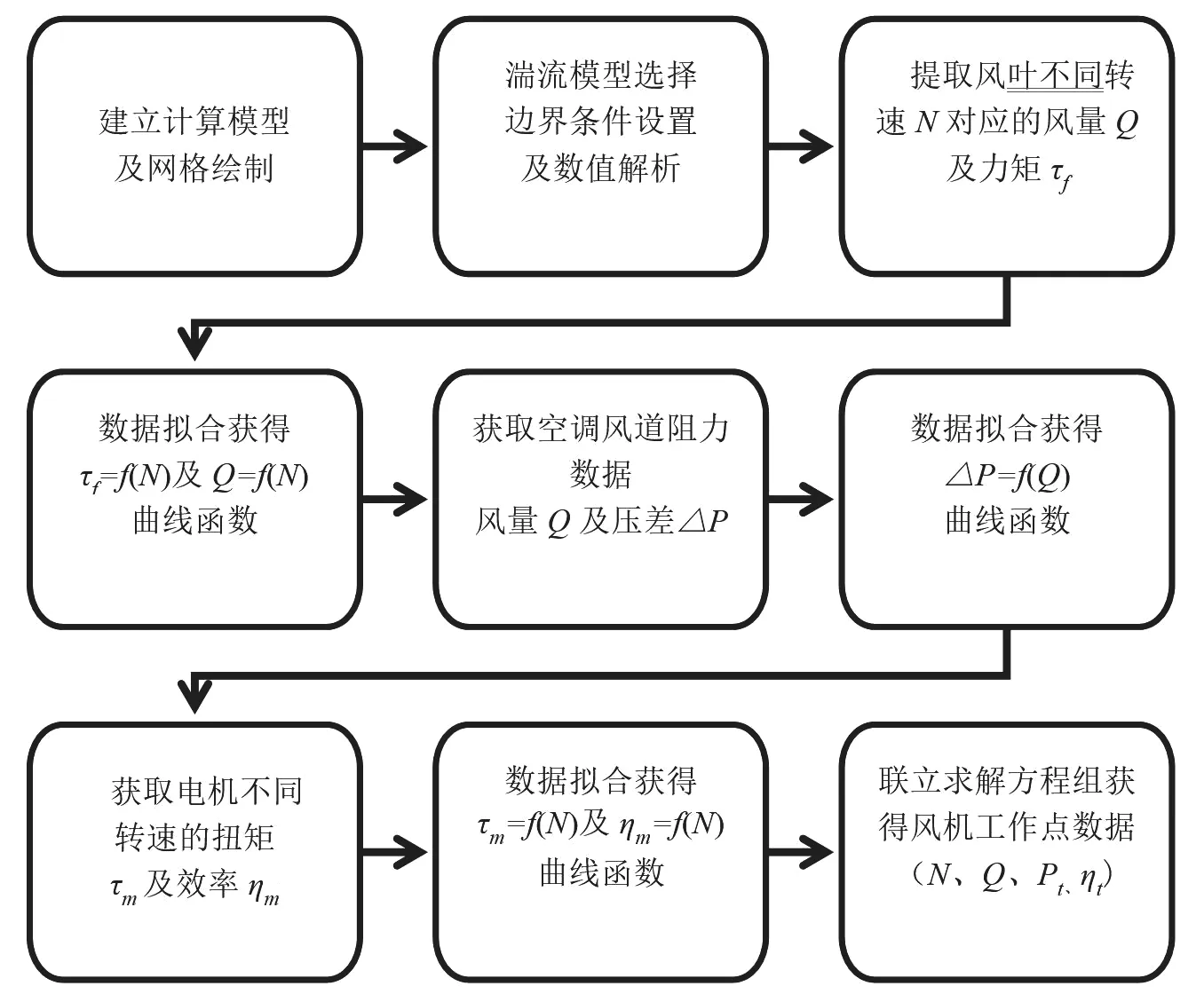
图5 交流风机工作点预测流程图

风叶的扭力-转速曲线难以采用直接测量的方式获得，但是其能够采用仿真计算的方法较容易的获得。针对研究的三款风叶的转速-扭力特性曲线以及测得电机的特性曲线如图6所示。

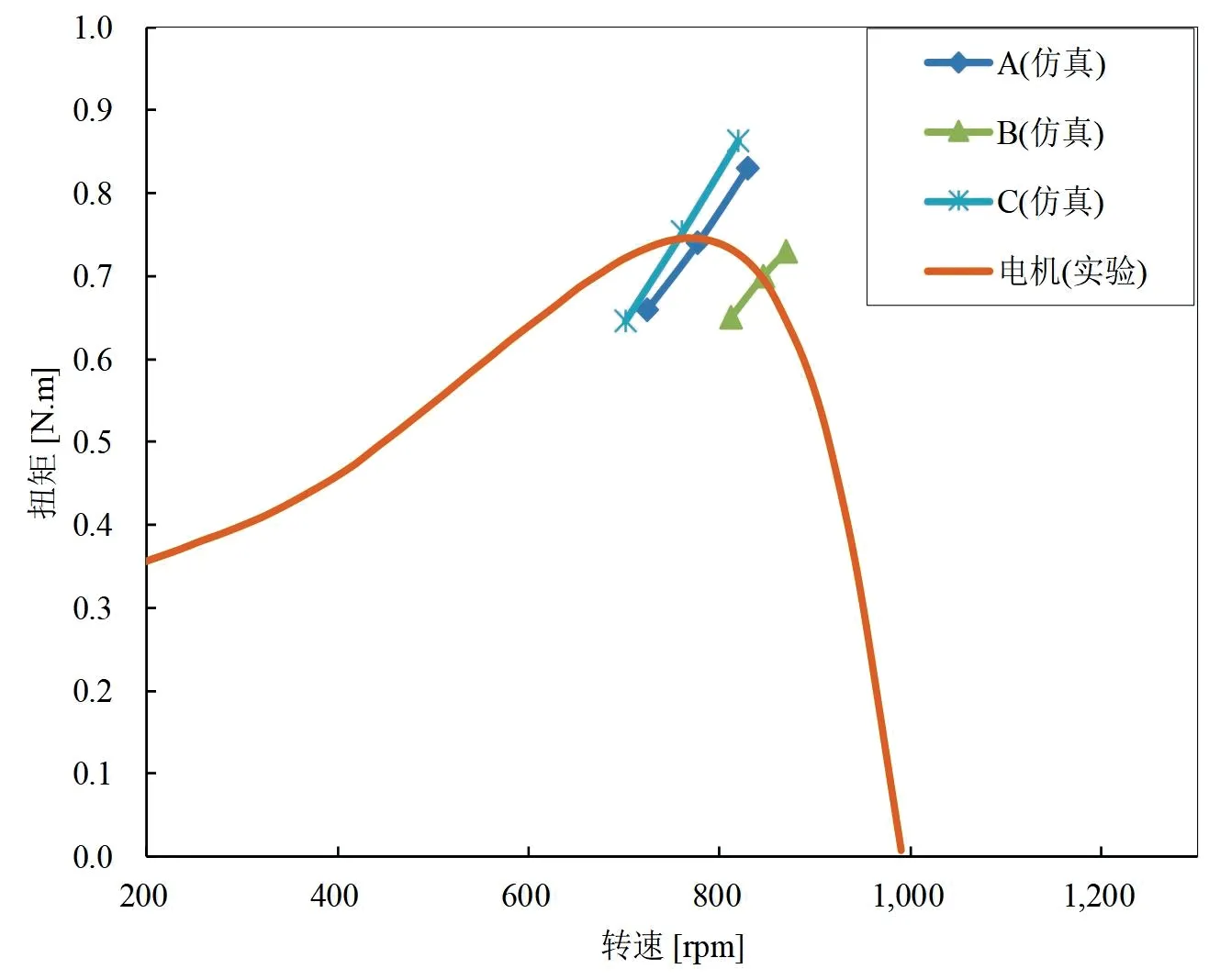
图6 风叶扭矩、交流电机扭矩与转速的对应关系

从图6中可看出：三款风叶的转速-扭力特性曲线会与电机的转速-扭力曲线分别相交于三点，该点即为风机在空调室外机中的工作点。为便于求解采用最小二乘法分别对上述4条曲线进行数据拟合。由于风机的转速与扭力存在平方的关系，因此采用二次多项式对其进行数据拟合如式（3）所示。在对电机转速-扭矩特性曲线拟合时，采用6次多项式以便取得较高的数据精度，如式（4）所示。上述拟合结果见式（5）～式（8），平均偏差差分别为0.174%、0.171%、0.179%及1.69%。

分别将式（5）～式（7）与式（8）联立求解，即可获得三款风叶与交流电机匹配所对应的工作转速N、工作扭矩τ。将转速N分别代入风叶的转速-风量特性曲线，N-Q曲线，即可获得所对应的工作流量Q，再联立风量-压力特性曲线，Q-Pt曲线，见图7，即可求解得到风叶工作压力Pt，由式（9）可计算得到风叶的效率ηf。再配合电机的转速-效率特性曲线，N-ηm曲线，见图8，即可获得电机工作效率ηm。最后由式（10）可得风机总效率ηt。三款风叶的计算结果以及实测结果如表2所示。

图7 室外机风道风量与压差的对应关系（实验）

图8 交流电机转速与效率对应关系（实验）

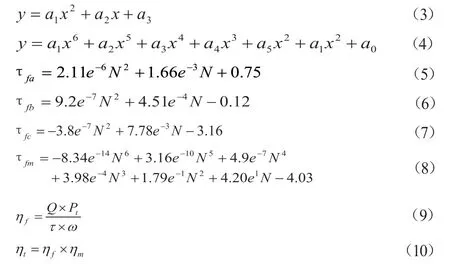
从表2可知，三款风叶基于上述方法的预测结果与实验测试结果的一致性良好，偏差＜5%。三款风叶在同一室外机内匹配同款交流电机时，工作转速不同，在各自对应的转速下风叶的风量、风叶的效率、电机的效率不同。结果显示：在三款风叶中，风叶A风量最高，有利于系统换热，风叶A的效率最高，达到69%，有利于整机提升能效。但是电机在风叶A工作转速下的效率较低，仅为44%，导致风机总效率不高。也就是说，风叶A与电机的不匹配，导致风叶A的高效特点没有得到充分发挥。风叶B与风叶C相比，虽然风叶B的效率相对较低，仅为56%，而风叶C的效率相对较高66%，但是其配套电机在其工作转速所对应的效率较高，54.5%，相对风叶C配套电机工作效率高12个百分点，致使其风机总效率较风机C高2.72个百分点。由此可见，风叶与电机合理匹配对于提高风机效率及整机能效相当重要，只有风叶效率与其配套电机效率均达到最高，风机总效率才能达到最高，才能实现最大限度的节能。假定将电机在777 r/min所对应的效率由44.6%提高到54.5%，则风机A的总效率可由更改前的30.7%提高到37.4%，提升幅度达到6.7个百分点，这对交流风机来讲是非常可观的。因此调整风叶A的配套电机的高效点，使其由高转速向低转速变化，将会使风叶A的功率进一步大幅降低。

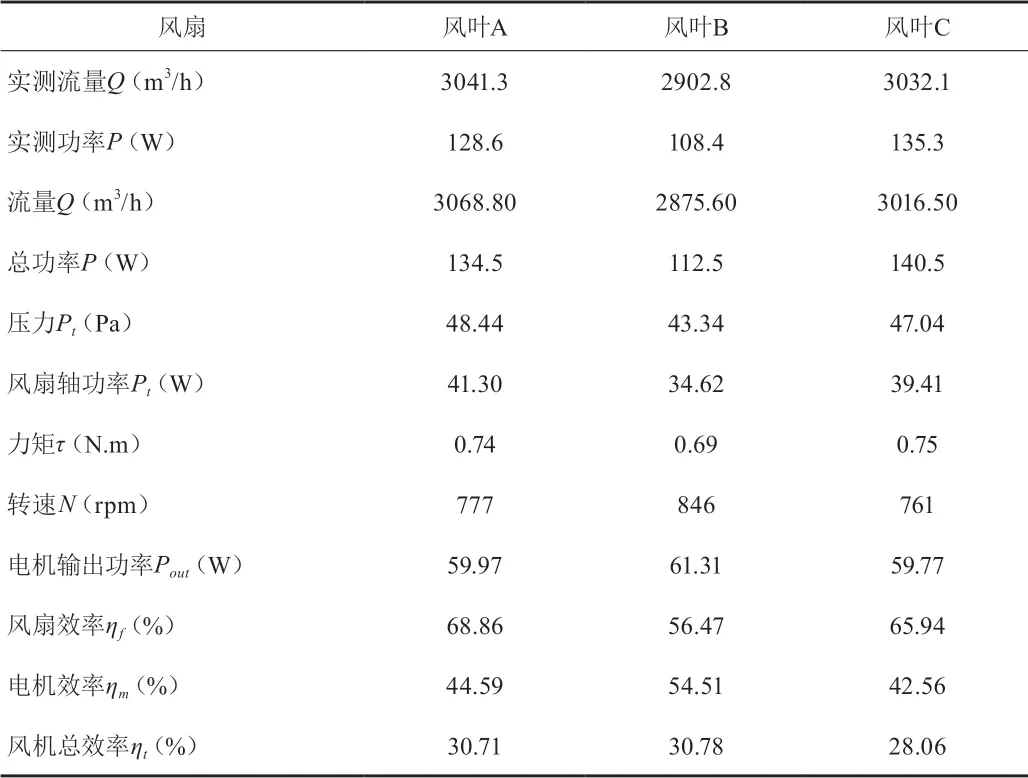
表2 三款风叶与某室外机风道匹配的测试结果及预测结果

4 结论

本文通过数值分析方法求解室外机风叶紊态流场，可准确获得风叶外特性数据，并且联合室外机阻力特性数据及交流电机转速扭矩特性数据，可准确预测交流室外机风机的实际工作点数据，预测结果与实际结果偏差＜5%，在产品开发过程中可有效指导风叶设计及选型。