相互作用的Brinkman-Forchheimer 方程组与Forchheimer 方程组的结构稳定性
张文彬,李远飞
(广州华商学院 数据科学学院,广东 广州511300)
0 引言
结构稳定性主要研究解对模型本身或者模型构建系数的连续依赖性与收敛性。有关结构稳定性的本质在Ames 和Straughan 的专著[1]中有详细的介绍,在Hirsch 和Smale 的专著[2]中介绍了连续流体力学模型中的结构稳定性。研究结构稳定性具有重要的意义,其原因在于建立模型的过程中不可避免地存在误差,需了解方程本身结构系数的微小变化是否会导致解的急剧变化。
当前关于结构稳定性的研究主要集中在多孔介质中的Brinkman、Darcy 和Forchheimer 方程组上[3-13],上述文献均是考虑在区域中只有一个方程组的情况。但在实际中,一个区域中可能存在两个或多个相互作用的流体方程组,因此有必要研究同一个区域中含有多个相互作用流体方程组的结构稳定性。由于不同方程组之间的相互作用,使得方程组解的性态变得复杂,从而导致研究的难度加大,故目前相关研究较少。关于其他类方程结构稳定性的研究可见文献[14-16]。
在文献[17]中Payne 和Straughan 建立了Brinkman 方程组与Darcy 方程组在一个界面相互作用的结构稳定性结果,研究了方程组的解对界面边界系数α1的连续依赖性的结果。随后刘炎等[18-19]在此基础上得到一些新的结果。而目前尚未发现研究相互作用的Brinkman-Forchheimer 方程组与Forchheimer 方程组界面问题的连续依赖性相关文献。如果将文献[17]中的Brinkman 方程组改为Brinkman-Forchheimer 方程组,将Darcy 方程组换成Forchheimer 方程组,如何处理非线性项|u|ui是本文研究的难点。
本文的目的是研究在多孔介质流中相互作用的Brinkman-Forchheimer 方程组与Forchheimer 方程组的解对Brinkman 系数μ的连续依赖性。平面Z=x3=0 的适当部分L是Ω1和Ω2中的共同边界,其中Ω1是x3>0 的区域,而Ω2是x3<0 的区域。即边界L是∂Ω1和∂Ω2的共同接触面。一方面,假设粘性流体在Ω1里是缓慢流动的,所以对应的是Brinkman-Forchheimer 方程组;另一方面,假设这个流体在Ω2中的多孔介质满足Forchheimer 方程组。界面用L表示,而Ω1和Ω2边界的其余边界部分分别用Γ1和Γ2表示,因此∂Ω1=Γ1∪L和∂Ω2=Γ2∪L。
在Ω1×[0,τ] 中讨论如下Forchheimer 流体方程组

其中:ui(i =1,2,3)、p、T 分别表示为速度、压强和温度;gi(x)(i =1,2,3) 为重力函数,假设gi满足| g | ≤G1;Δ 为拉普拉斯算子;k 为热扩散系数;Ω1是R3中的一个有界单连通的星形区域;τ 是给定的常数且0 ≤τ <∞。
在Ω2×[0,τ] 中讨论如下Darcy 流体方程组

其中:vi(i =1,2,3)、q、S 分别表示为速度、压强和温度;kS为热扩散系数;Ω2是R3中的一个有界单连通的星形区域。

1 先验界
为了得到本文的主要结果,给出以下引理。
引理1[20]温度T 和S 满足以下最大值估计



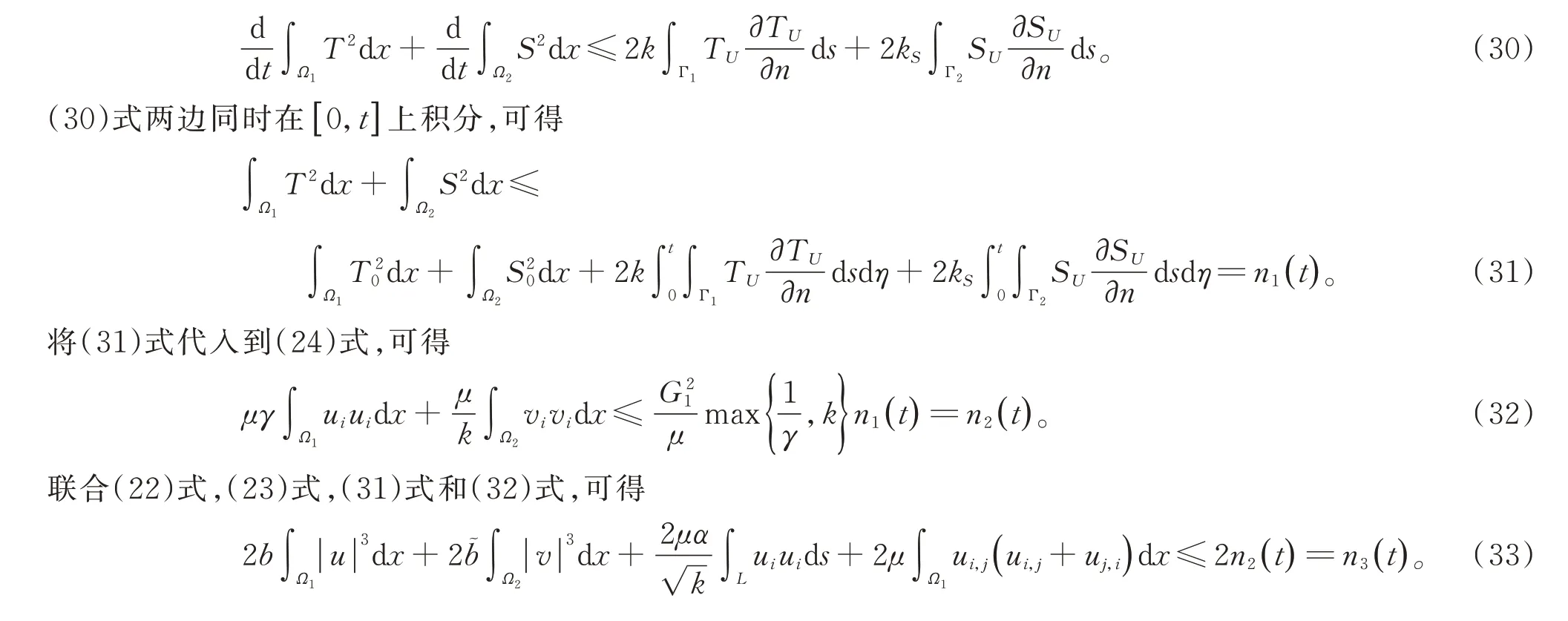
2 系数μ 的连续依赖性



3 结论
本文得到相互作用的Brinkman-Forchheimer 方程组与Forchheimer 方程组的解对系数μ 的连续依赖性结果。运用本文的方法也可得到解对其他系数的连续依赖性。本文的结果说明对于相互作用的此类方程组具有结构稳定性,同时该结论也为后续数值模拟与数值计算提供理论基础。

