万瓦级舰载激光武器反无人机作战效力研究
徐粲然,孙世岩,佘 博,周锦锋
(1.海军工程大学 兵器工程学院, 武汉 430000; 2.海装驻上海地区第二军代室, 上海 200126)
1 引言
激光武器是通过热烧灼作用使目标受热熔融或爆炸的一种新型定向能武器。由于目标表面的毁伤程度与激光照射时长和出光功率相关,因此通过调节激光武器的打击时长和出光功率,可对无人机进行干扰、致盲、摧毁等分级式毁伤。其中干扰和致盲可定义为对目标实施软毁伤,摧毁可以定义为对目标实施硬毁伤。考虑舰载万瓦级激光武器兼具对目标进行软硬2种毁伤方式的特性,根据不同军事需求,利用万瓦级激光武器对目标实施分级拦截,即可在不击毁敌方目标的情况下保护我国军事秘密安全,又可配合其他传统舰载武器对目标实施打击拦截,提升打击能力。因此对舰载万瓦级激光武器在海洋环境下的作战效力研究具有一定的现实意义[1-6]。
激光武器从开始研究已经有几十年的发展历史。目前,国内对激光武器的毁伤机理的分析已较为完善,对激光辐照材料烧灼情况、激光在大气中的传输衰减、激光对材料的毁伤情况等也具有相关实验和研究。如刘霞等[7]搭建了激光在雾中传输的衰减实验平台,研究了激光衰减系数与雾水平能见度的关系。赵杨等[8]就激光辐照材料烧蚀特性进行了数值仿真。但将各模块进行整合并针对典型目标最终给出激光武器有效毁伤距离及毁伤概率的研究相对较少,理论数据较为缺乏。
本研究对激光武器毁伤过程进行分析,建立了激光武器毁伤模型并进行相关计算。通过对目标进行模型等效,考虑海面大气环境对激光光束质量的影响,结合激光武器跟瞄系统的跟踪精度给出了激光武器的到靶功率密度及能量密度,讨论了不同大气能见度环境下激光武器的最佳拦截半径及毁伤概率。
2 典型目标选取
根据用途分类,无人机可分为侦察无人机、察打一体无人机、运输无人机3种。其中侦察无人机和查打一体无人机占比较大。MQ-8C “火力侦察兵”是美国应用较广泛的舰载垂直起降无人机,主要部署在濒海战斗舰及水面舰艇上,用于执行侦察、攻击及补给任务。其性能较为优越,可装载光电/红外传感器,曾多次出动用于侦察和瞄准任务,是较为典型的无人机目标。MQ-8C “火力侦察兵”性能参数值如表1所示[9-10]。

表1 MQ-8C “火力侦察兵”性能参数
“火力侦察兵”采用的机载雷达为AN/ZPY-8“鱼鹰”雷达,处理器尺寸为200 mm×125 mm×230 mm。机载光电侦察设备为HMOSP,其中包括热像仪和电视摄像机,转塔尺寸为500(h)mm×380(d)mm,质量<32 kg,电视摄机现场为0.9°×0.67°(窄),3.3°×2.5°(中),12°×9°(宽)。
激光武器通过对无人机油箱、机翼、尾翼等关键部件损伤可达到硬毁伤目的。通过辐射使机载雷达天线罩、导航天线等失效可达到软毁伤目的。无人机机身、机翼等部位多以结构复合蒙皮材料制成,油箱多以玻璃纤维/蜂窝芯蒙皮、碳纤维/蜂窝芯蒙皮为表皮材料。参考毁伤无人机油箱实验,无人机不同材料及毁伤阈值如表2所示[11]。
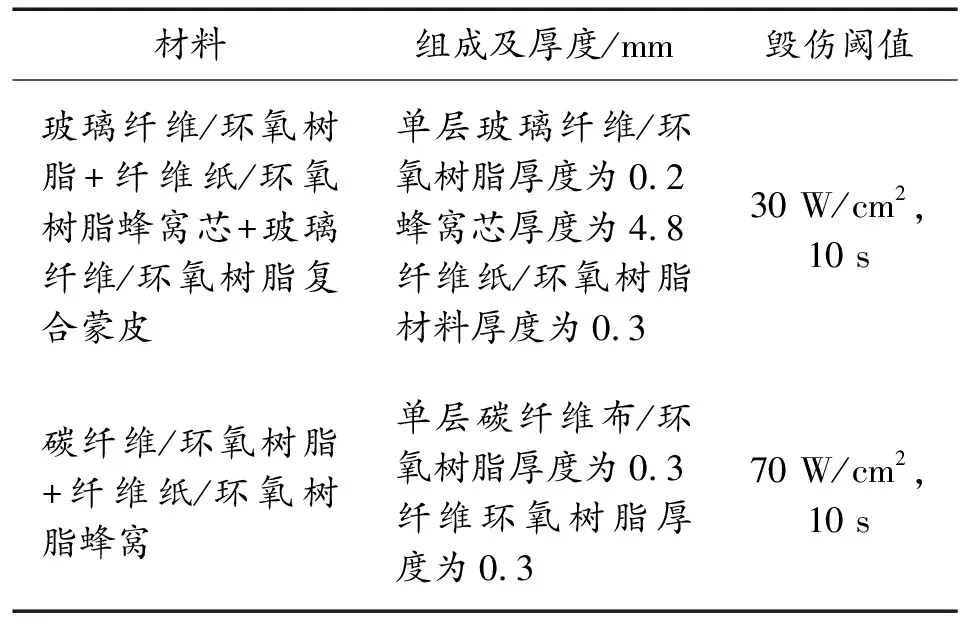
表2 无人机采用材料及组成
基于对激光武器的使命与定位分析,仿真以MQ-8C “火力侦察兵”无人机为典型目标,选取其相关参数进行仿真。分析计算激光武器对MQ-8C “火力侦察兵”无人机载光电侦察设备实施致盲及硬拦截毁伤概率及最佳拦截半径。
3 效力仿真模型的建立
为研究激光武器的毁伤效能,需考虑影响激光武器射击结果的诸多因素,如大气传输对激光光束质量的影响,跟瞄精度对射中目标面积的影响,目标材料的受热程度等。效力仿真主要流程如图1所示。
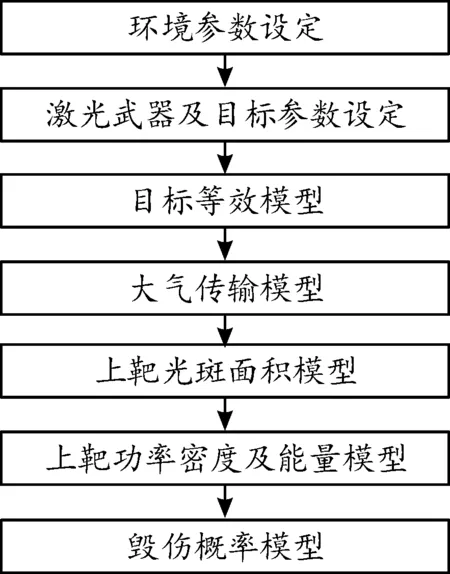
图1 激光武器毁伤效力仿真流程框图Fig.1 Simulation process for laser weapon damage effectiveness
仿真分析由目标等效模型、大气传输模型、上靶光斑面积模型、上靶功率密度及能量密度模型和毁伤概率模型5个模块组成。首先对作战环境参数及激光武器参数、目标毁伤阈值进行设定。在目标等效模型中,将目标抽象为三维坐标系中的一个点,通过对坐标进行计算不断实时更新自身运动参数,得到激光武器与目标间的实时射程及激光光束与目标之间的夹角。通过大气传输光束质量衰减模型可求得综合大气各衰减因素后激光光束质量。利用蒙特卡洛法模拟射击跟瞄精度,进而求得到靶远场光斑面积、到靶功率密度及到靶能量密度。根据到靶参数与毁伤阈值的关系判断是否毁伤,计算激光武器最佳毁伤半径及毁伤概率。
3.1 目标等效模型
激光武器的毁伤效能评估建立在打击目标的基础上,研究激光光束的指向过程,首先需要建立目标等效模型。为简化目标航路,将目标假定为一个做匀速直线运动的等密度长方体。仿真从目标水平飞行及目标俯冲飞行2种飞行姿态进行分析。当目标俯冲角θm为0°时,目标为水平飞行。当目标具有一定俯冲角度时,目标为俯冲飞行。
将目标位置抽象为一个坐标点,建立目标笛卡尔坐标系,x为水平方向,xoz为水平面,y为竖直方向。
设目标初始位置为(x0,y0,z0),俯冲角为q。则目标的初始方位角F可表示为:
F=atan(z0/x0)
(1)
假定Vm为目标的速度(m/s);θm为目标的俯冲角(-π/2≤θm≤0),z0为航路捷径。则:

(2)
设i代表时刻,则在i时刻目标位置可表示为:
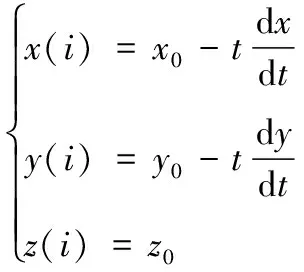
(3)
将目标坐标系(x,y,z)变换为地理坐标系(X,Y,Z),坐标变换如下:

激光武器与目标间斜距可表示为:

(4)
激光武器的高低角ε及方位角β可表为:

(5)
目标的高低角εm及方位角βm可表示为:
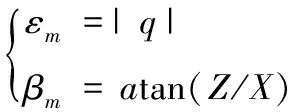
(6)
3.2 大气传输模型
大气传输模型主要从大气衰减和大气湍流效应两方面进行考虑。激光武器在大气中传输受大气吸收及散射等因素影响。在不考虑热晕效应等非线性效应影响的条件下,依据目标特性,在水平传输条件下大气传输效应计算[12-15],有:
(7)
在斜程传输条件下大气传输效应计算,有:
T=exp(-secθK/V)[1-exp(-0,835Rcosθ)]
(8)
其中:
θ=(π/2-ε)
(9)

式中:T为大气透过率;V为大气能见距;R为激光武器与目标间实时传输距离;K为气溶胶模型常数,海上作战环境下取4.453;λ为激光发射波长;θ为天顶角;ε为激光武器高低角;q修正因子。大气湍流会导致激光光束质量下降,引用modified hufnagel-valley(MHV)湍流模型计算折射率结构常数[16]:
3.02×10-17exp(-h/1 500)+
1.90×10-15exp(-h/100)
(10)
式中:h为目标实时高度。
根据经验公式,光束通过湍流效应后,光束横截面上的两点之间相位保持相干的最大距离r0可由下式进行估算
(11)

大气湍流所产生的光束质量因子为:
βt≈(1+0.62(D/r0)5/3)1/2
(12)
设激光武器初始发射光束质量为βf,则经过大气湍流影响后的光束质量为
β=(βf+βt)1/2
(13)
3.3 上靶光斑面积模型
由于大气光学传输作用,远场光斑形状会发生畸变。产生一定的发散角,则在射击距离为R上的远场激光照射区域半径r1[12]:

(14)
式中:β为综合大气湍流影响后的光束质量;λ为激光发射波长;R为激光武器与目标间实时传输距离;D为激光发射口径。考虑光束与目标间存在一定夹角,激光武器对目标的打击方式形式可分为迎头打击或侧向打击。设定当光束与目标间夹角小于30度时定义为迎头打击,当光束与目标间夹角大于30度时定义为侧向打击。则迎头打击下理想光束投影面积为:
(15)
侧向打击下理想光束投影面积为:
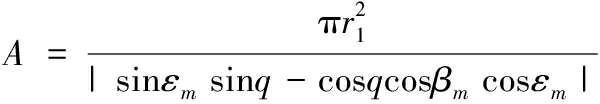
(16)
式中:A为不考虑射击误差时的理想光束投影面积;r1为远场激光照射区域半径;ε为激光武器高低角;β为激光武器方位角;εm为目标高低角;βm为目标方位角;q为目标俯冲角,仿真时可根据目标航线进行取值。
远场到靶光斑面积是计算激光武器效能的重要指标,为更准确地计算远场到靶功率密度,应考虑受跟瞄精度及射击误差影响。根据蒙特卡洛法,将跟瞄误差与射击误差表示为高低角方位角均服从正态分布的均值为0,均方差为10微弧的随机数[17],该随机数每步长进行一次更新,生成新的光斑中心坐标。
假设某时刻瞬时光斑中心坐标为(x,y,z),目标区域中心坐标为(X,Y,Z),则两者间距离为
(17)
其中当目标俯冲角q=0时,瞬时光斑中心坐标为:
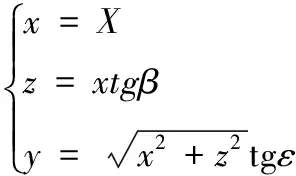
(18)
当目标俯冲角q>0时,瞬瞬时光斑中心坐标为:

(19)
式中:ε为激光武器高低角;β为激光武器方位角;q为目标俯冲角。
根据远场激光照射区域与目标靶面圆区域的位置关系,可求得综合考虑射击误差后的光斑重叠面积SJ。
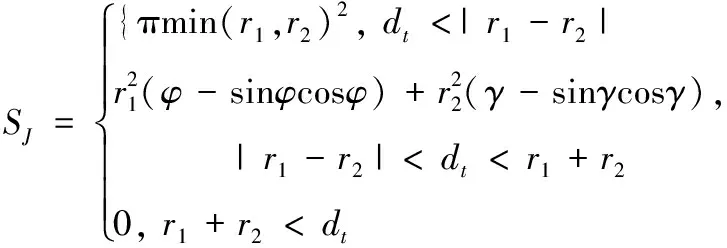
(20)
其中:
式中:r1为远场激光照射区域半径,r2为目标靶面圆区域半径,dt为瞬间光斑中心与目标区域中心距离。
3.4 上靶功率密度及能量密度模型
设激光发射功率为P0,经过大气衰减后其激光远场功率Pr为:
Pr=P0T
(21)
上靶功率密度Ir(t)计算为:
(22)
式中:K1为含能系数,取值为0.84;A为上靶光斑面积;Pr为激光远场功率。
假设将一次射击从第0秒开始到第n秒结束,则目标吸收的总能量W及能量密度E可表示为:
W=Ir(t)SJσ
(23)
(24)
式中:σ为目标材料能量吸收系数,取值0.8;SJ为重叠面积;r2为目标区域半径,取值0.01m。
3.5 毁伤概率模型
激光武器毁伤目标程度受上靶功率密度和能量密度两方面影响[18]。上靶功率密度是衡量远场激光毁伤强度的指标,当上靶功率密度不足时,激光强度不足以对目标造成伤害。能量密度是达到毁伤强度的时间累加值,与上靶时长和上靶功率密度相关。当能量密度不足时,毁伤时间不足不能毁伤目标。
根据目标上靶功率密度Pr及功率密度阈值Pr0的关系及一次射击后累计能量密度E与能量密度阈值E0的关系,可建立激光武器毁伤判据模型。
E0(KJ/cm2)=Pr0(W/cm2)×T(s)
(25)

激光武器对无人机的毁伤可分为硬毁伤和软毁伤2种。硬毁伤是激光辐射无人机易燃易爆部位,使其受热爆炸导致无人机解体。软毁伤是激光武器辐射无人机光电导引头等部位,使其受热丧失部分功能。由于毁伤方式相同,可通过设定不同功率密度及能量密度阈值方式,对2种毁伤方式的效能进行分别求取。假设对目标毁伤阈值如表3所示。

表3 功率密度与能量密度毁伤阈值表
毁伤概率定义为激光武器对目标实施攻击时,上靶功率密度及能量密度均达到毁伤阈值的概率,是综合反映毁伤作战效能的重要指标,它可以反映在一定的距离下,特定的环境中,打击某一目标成功的可能性大小。为直观的测试激光武器的毁伤效果,仿真计算了全航路毁伤概率。
假设程序仿真一次即为一次射击,共进行N次仿真,将成功毁伤的次数累加起来记为K,全航路毁伤概率记为PK,则当样本足够大时,PK将无限趋近于某一数值。
4 仿真分析
假设某舰载激光武器指标参数有:激光波长为1.06 μm,发射光束质量为3,发射望远镜直径为0.3 m,平均发射功率为30 kW,跟踪瞄准精度为10 μrad;速度77 ms程序总模拟次数为1 000次,时间步长0.01 s。仿真按2种毁伤阈值情况分别进行分析
1) 对目标进行软毁伤情况下:假设目标俯冲姿态飞行初始高度3 000 m,初始距离5 000 m,俯冲角度5度;分别计算能见度为15 km及25 km环境条件下的毁伤概率。
2) 对目标进行硬毁伤情况下:假设目标俯冲姿态飞行初始高度2 000 m,初始距离2 500 m,俯冲角度5°;分别计算能见度为15 km及25 km环境条件下的毁伤概率。
4.1 仿真结果
1) 软毁伤阈值下仿真结果
软毁伤阈值下仿真结果如图2、图3所示。

图2 15 km能见距条件下毁伤概率曲线Fig.2 Probability curve of damage under 15 km visibility

图3 25 km能见距条件下毁伤概率曲线Fig.3 Probability curve of damage under 25 km visibility
2) 硬毁伤阈值下仿真结果
硬毁伤阈值下仿真结果如图4、图5所示。

图4 15 km能见距条件下毁伤概率曲线Fig.4 Probability curve of damage under 15 km visibility
4.2 仿真结果分析
通过程序仿真计算,按照毁伤概率不小于99%为标准统计激光武器的有效毁伤距离,当目标处于俯冲飞行姿态,初始飞行高度为3 000 m,初始距离为5 000 m,能见距为15 km时,软毁伤有效毁伤距离为4 380 m;能见距为25 km时,软毁伤有效毁伤距离为4 890 m。
当目标处于俯冲飞行姿态,初始飞行高度为2 000 m,初始距离为2 500 m,能见距为15 km时,硬毁伤有效毁伤距离为1 720 m;能见距为25 km时,硬毁伤有效毁伤距离为1 990 m;由概率毁伤曲线图可见,激光武器毁伤距离受大气能见度影响,能见距越大毁伤距离越远。其关系如图6所示。

图5 25 km能见距条件下毁伤概率曲线Fig.5 Probability curve of damage under 25 km visibility
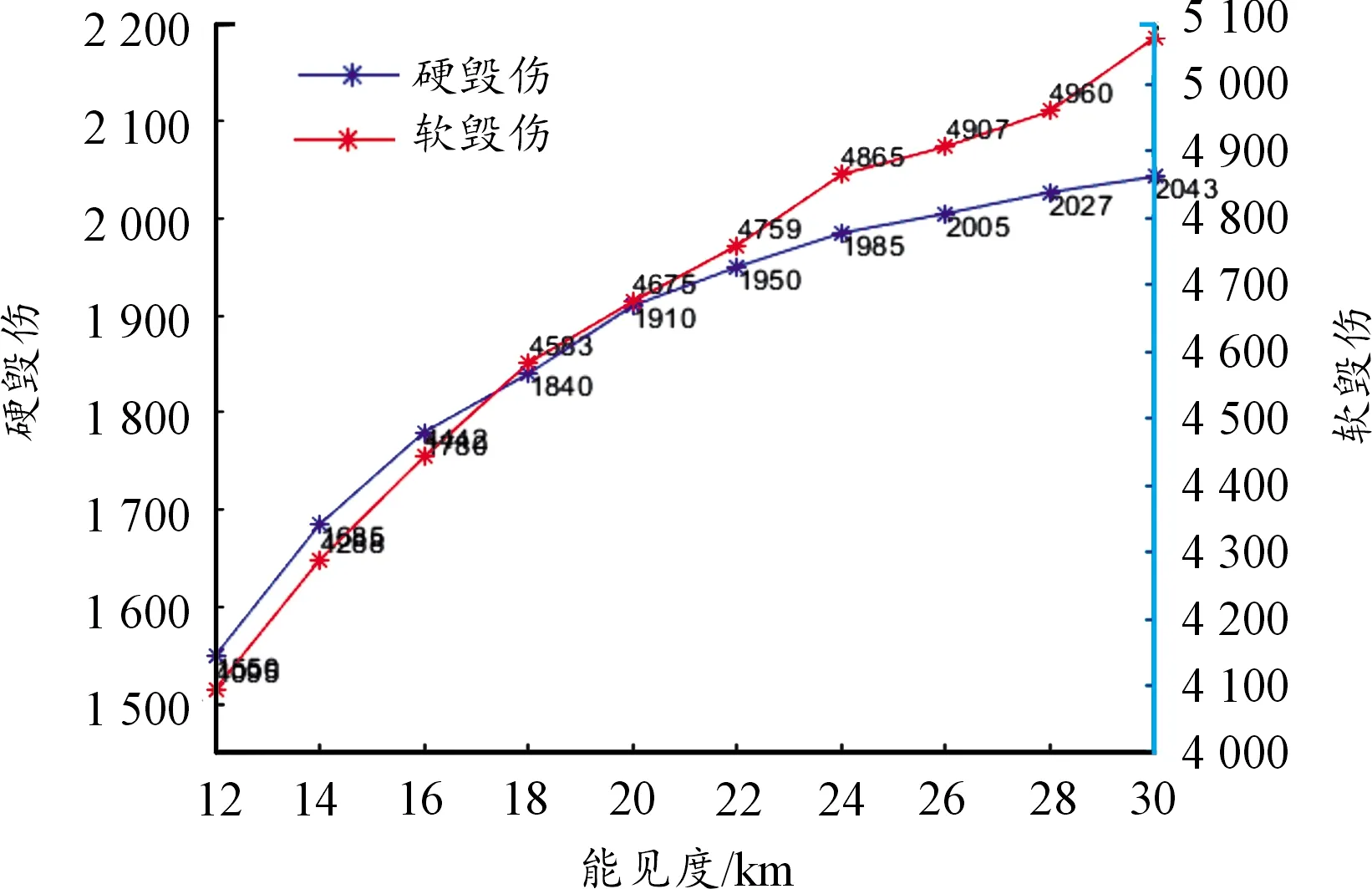
图6 能见距与最大毁伤距离曲线Fig.6 The distance can be seen with the maximum damage distance curve
若将激光武器的出光功率调整为100 kW,软毁伤初始距离调整为9 500 m,硬毁伤初始距离调整为5 000 m,其他参数不变,其能见度与毁伤距离关系如图7所示。可以看出,增大出光功率可增大有效毁伤距离,从而适当克服能 见度对激光武器有效毁伤距离的影响。
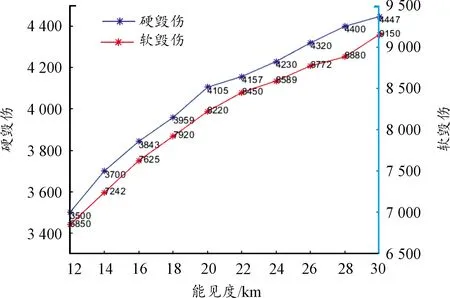
图7 能见度与最大毁伤距离曲线Fig.7 The distance can be seen with the maximum damage distance curve
5 结论
将对激光武器的作战效能分析进行模块化处理,建立了目标等效模型、大气传输模型、上靶光斑面积模型、上靶功率密度及能量密度模型、毁伤概率模型5个仿真模块,计算了激光武器光束从发射到到靶这一过程中的能量变化,仿真分析了舰载激光武器在不同能见度条件下的有效毁伤距离及毁伤概率。在对传输过程和毁伤过程计算时,做了部分简化,后期还需进行优化并进行验证。

