基于神经网络的变后掠翼飞行器自适应控制方法研究

李墨吟，马泽远，周建平，张云飞，夏群利

(北京理工大学宇航学院，北京 100081)

0 引言

变形飞行器作为一种新概念飞行器，在未来民用和军用领域都有着广泛的应用前景，其变形方式包含了变展长、变弦长、变厚度、变后掠以及变弯度等。本质上，变形飞行器可以认为是一类涵盖了多种气动性能模式的特殊飞行器，不同的气动性能可适用的作战场景与任务也不同。例如，远程打击作战场景中，飞行器需要更大的航程，此时，大升阻比的气动构型能够为飞行器提供足够的升力以保证续航飞行能力，而在末段俯冲打击任务中，更小的阻力，更大的侧向过载能力能够增强飞行器的突防能力。因而，变形飞行器研究逐渐成为学术界和工程界的研究热点[1-4]。

近年来，随着现代控制理论的推进，各种新型控制方法应运而生，对于传统飞行器，张广勇等[5]在动态逆控制律的基础上，利用神经网络进行误差补偿实现了自适应控制。刘晓岑等[6]针对高超飞行器姿态控制问题，在考虑输入饱和的情况下，设计了具有强鲁棒性的基于滑模观测器的动态面控制方法，该方法能够保证控制输入更平滑且尖峰值更小。而对于变形飞行器控制问题，聂博文等[7]研究了一种可折叠变形的飞行器过渡飞行控制策略，针对垂直起降和高速巡航模态状态衔接问题，通过试验验证了该方案的有效性。郑曼曼[8]利用T-S模糊理论描述整个变体过程，以此设计了T-S模糊飞行控制器。熊英等[9]针对变后掠翼飞行器，研究并设计了非线性多模型切换系统，利用非线性干扰观测器对复合干扰逼近以实现姿态跟踪。而人工神经网络[10-11]作为一类具有逼近任意函数功能的系统，可以实现在复杂环境下的自适应控制。对于变后掠翼飞行器而言，变后掠角过程中气动参数的改变对于控制系统提出了一定的挑战，因此有必要研究针对该类飞行器的自适应控制律。

文中研究了变后掠角过程中飞行器姿态稳定控制问题。首先利用气动仿真软件Datcom建立了变后掠翼飞行器在不同形变状态下的气动模型。然后建立适应变后掠翼飞行器姿态动力学、运动学模型，并利用动态逆理论处理该类飞行器姿态运动模型中的强耦合问题，在此基础上，将PID参数设置为神经网络隐藏层的节点，实现PID参数自适应调整。进一步地，研究了存在外界干扰下的变后掠翼飞行器姿态稳定控制问题。最后仿真结果验证了其有效性。

1 考虑变形参量的飞行器姿态运动模型

在研究变后掠翼飞行器姿态控制问题中做出如下几点假设：

1)飞行器为刚体，且在变形过程中速度、质量保持不变；

2)地面坐标轴系为惯性坐标系；

3)忽略地球自转，将地球看作均匀质量圆球。

针对面对称的变后掠翼飞行器，建立如下考虑变形参量的无动力飞行姿态运动方程组[6]：

(1)

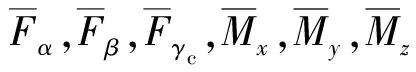
2 变后掠翼飞行器气动模型建立

变后掠翼飞行器构型如图1所示，其头部为圆锥，弹身为圆柱，两侧为面积较大的梯形升力翼，提供飞行过程中大部分的气动力，控制舵位于弹身尾部，呈“+”型分布，可提供少部分气动力。

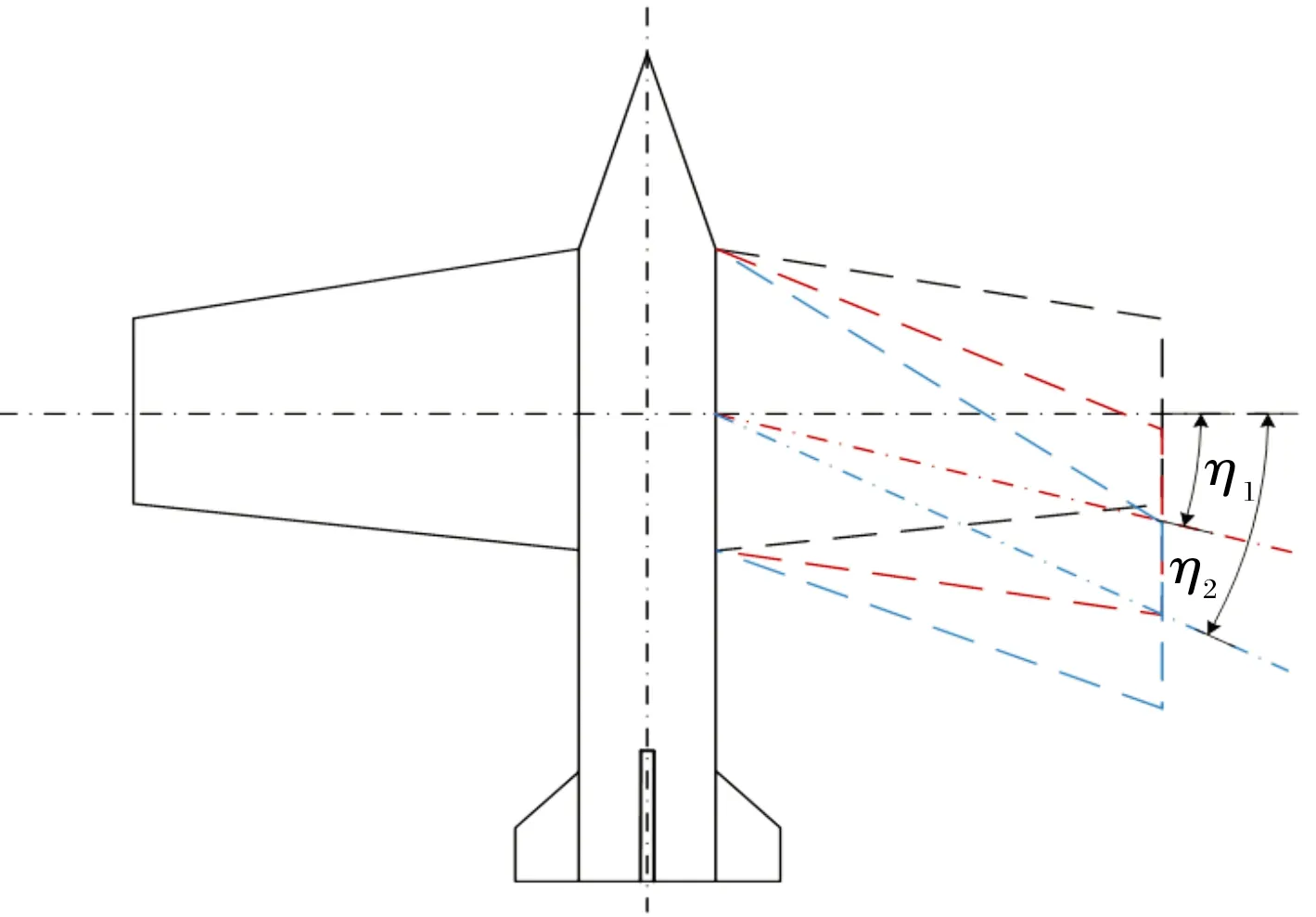
图1 变后掠翼飞行器示意图

变后掠翼通过改变后掠角来改变飞行器的气动性能，在工程中已被一些飞行器采用，因此文中基于该变形方式，利用气动仿真软件Datcom，计算不同后掠角状态下的飞行器气动特性，以此建立变后掠角飞行器的气动与变形量之间的函数。

考虑后掠角变化范围在0°～60°，以30°,60°后掠角的升力系数、俯仰力矩系数为例，其气动特性如图2～图5所示。

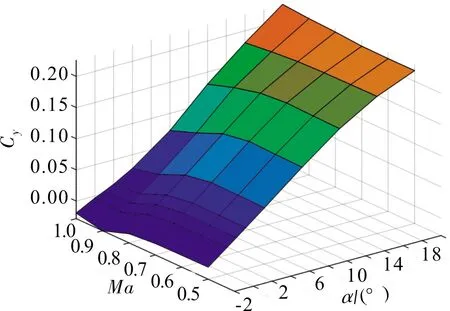
图2 30°后掠角下的升力系数

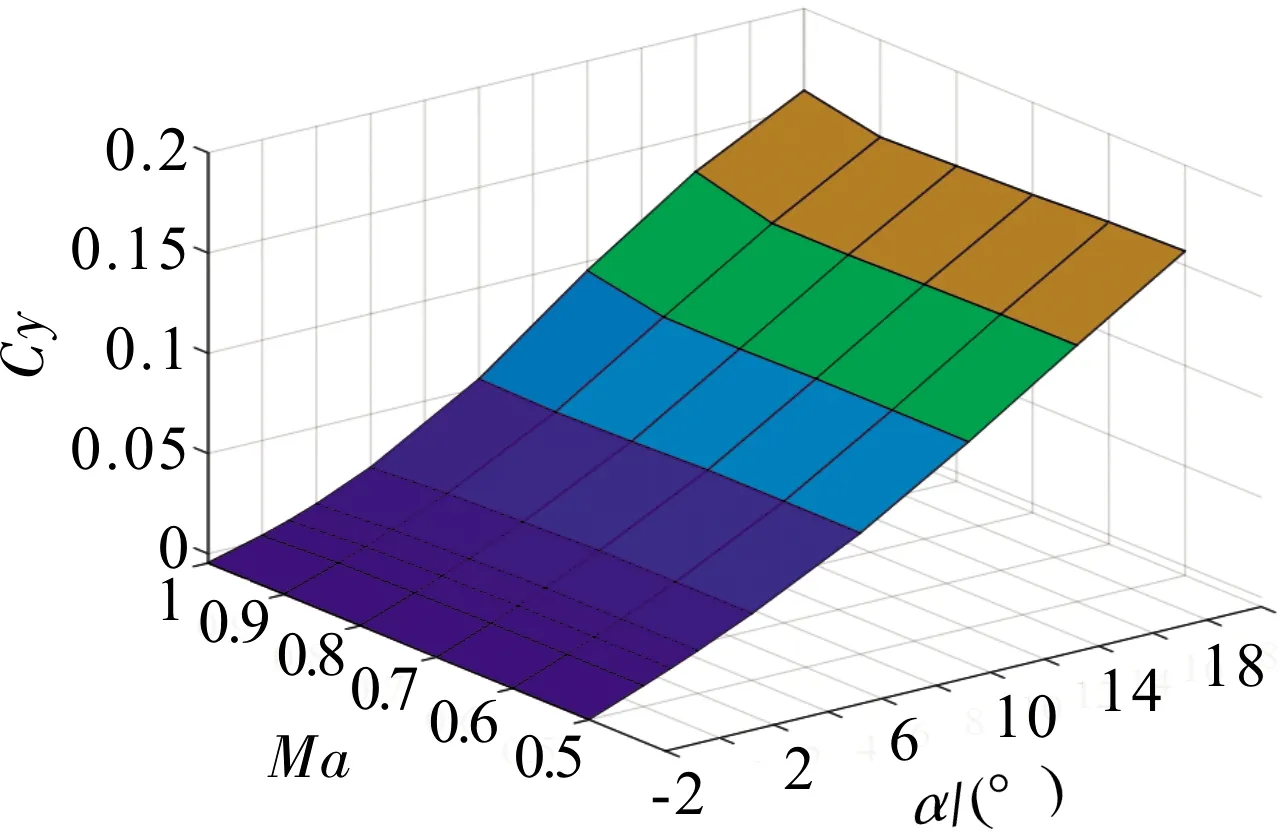
图3 60°后掠角下的升力系数

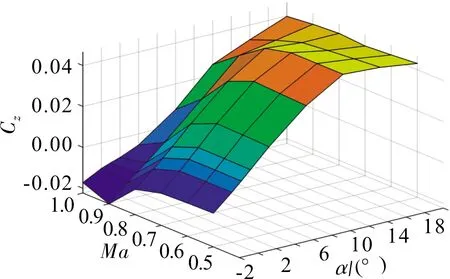
图4 30°后掠角下的俯仰力矩系数

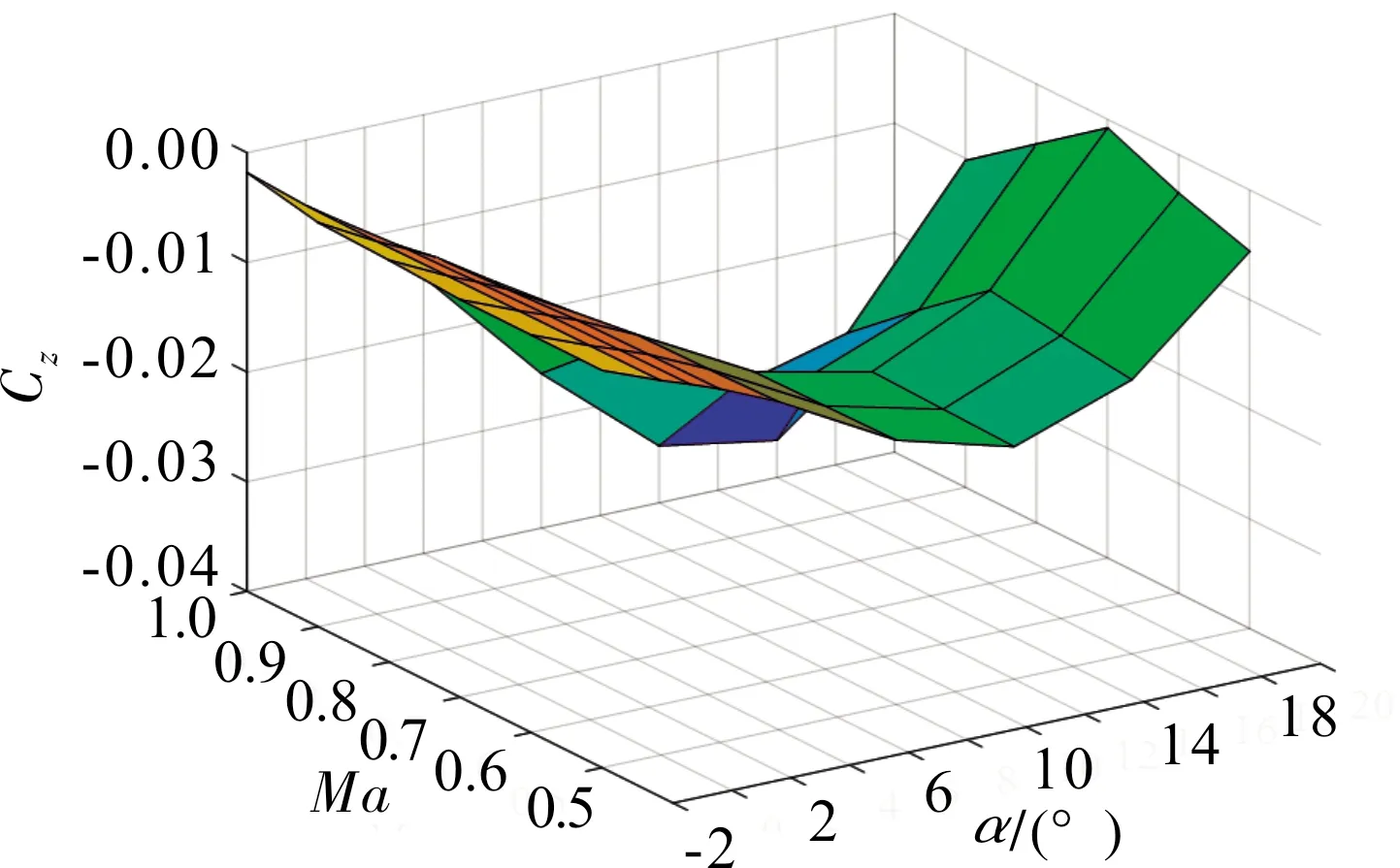
图5 60°后掠角下的俯仰力矩系数

根据Datcom计算得到的气动数据，建立包含形变参量的飞行器气动力和气动力矩表达式：

(2)

式中：q,S,l为动压、飞行器参考面积及参考长度；CY(η),CZ(η)为升力系数、侧力系数；Cx(η),Cy(η),Cz(η)为滚转、偏航、俯仰力矩系数。为了更好的实现控制器的设计，可以将气动系数在特征点处拟合成线性化形式，如式(3)所示：

(3)

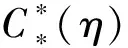
综上，结合第1节中的飞行器姿态运动方程式(1)，建立了包含不同后掠角的气动特性变后掠翼飞行器姿态运动学动力学模型。

3 基于神经网络的PID自适应动态逆控制方法

3.1 动态逆控制结构

由运动方程式(1)可知，系统的状态变量有α,β,γc,ωx,ωy,ωz共6个，而系统的控制变量只有δx,δy,δz，由于动态逆控制方法需要控制对象满足控制量与状态量个数相等，因此根据奇异摄动理论需要对状态变量进行时标分离。考虑飞行器姿态角变化相对于角速度变化慢，由此将整个飞行器姿态控制系统划分为慢变子系统和快变子系统。结合式(1)～式(3)建立面向变后掠翼飞行器姿态动态逆控制的状态方程[6]：

(4)

式中:x1=[αβγc]T，x2=[ωxωyωz]T代表状态量;u=[δxδyδz]T为控制变量。第一个公式代表慢变量回路，第二个公式代表快变量回路。ξ1,ξ2为飞行器所受到的外界干扰。f1(x1,θ)，g1(x1)，f2(x1,x2)，g2(x2)具体形式如式(5)～式(8)。

(5)

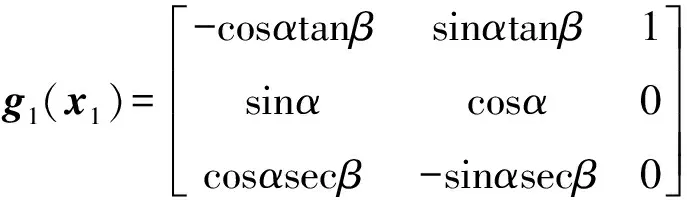
(6)

(7)

(8)

其中，当侧滑角β≠±90°时，矩阵g1(x1)可逆。综上，可得变后掠翼飞行器快慢子系统控制律为：

(9)

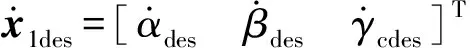
3.2 基于神经网络的PID自适应控制器设计

在实际飞行过程中，PID参数通常是预置好的，而在变形过程中，预置参数不一定完全适应整个飞行过程，因此，提出了一种利用神经网络对PID参数进行自适应调整的策略，使得控制器能够在飞行器变形过程中实时调节PID参数。该方法将PID的3个参数设置为神经网络隐藏层中的基函数，通过不断计算当前控制参数对被控对象的状态影响进行迭代训练，采用梯度下降的策略对输出层的权重进行调整，神经网络PID自适应控制器结构如图6所示。

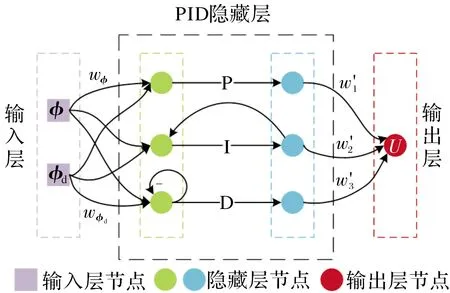
图6 神经网络PID控制结构

该网络结构的输入包含状态量的期望值φd与状态量的实际值φ，即：

(10)

(11)

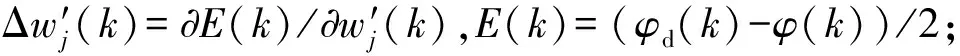
结合式(11)，给出基于神经网络的PID自适应控制律为：

(12)

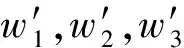
(13)

对于该控制律，为保证系统稳定，需要ΔE<0，根据式(13)可得：

(14)

综上，建立的针对变后掠翼飞行器控制系统流程如图7所示。

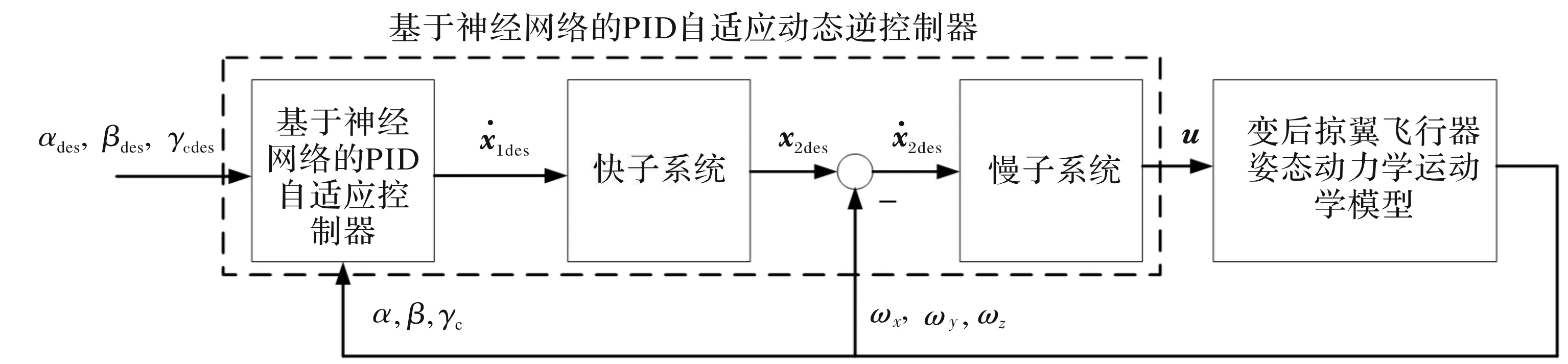
图7 变后掠飞行器控制系统流程图

4 仿真分析

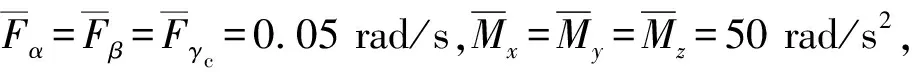
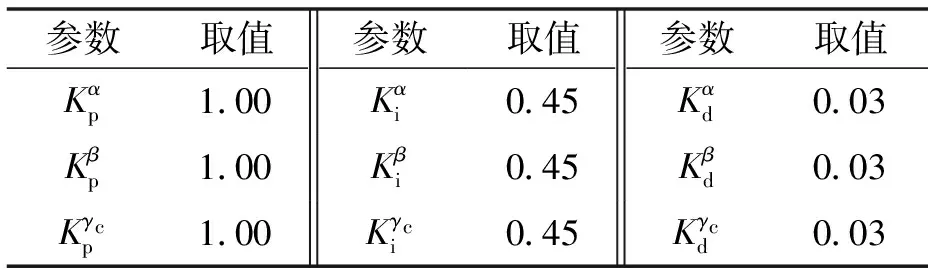
表1 控制器初始参数设置

图8～图10展示了基于神经网络动态逆PID自适应控制律的跟踪效果，对比可以看出：文中提出的控制律在响应速度、超调等方面均优于传统的动态逆PID控制律，姿态跟踪的超调相比传统控制律下降了33.03%～40.52%，干扰产生的扰动下降了42.33%～75%。从图11～图13可以看出：由于动态逆控制方法将变后掠飞行器在变形过程中的气动参数引入到了控制量中，在t=[1 s,2 s]的变后掠角过程中，该控制律能够有效稳定住飞行器的姿态;当t=3 s时，飞行器在外部干扰下，自适应控制律能够在充分利用舵机资源的情况下迅速的稳定飞行器姿态，因此，该方案具有更合理的输入控制设计，能有效调度控制资源，提升系统的控制性能。

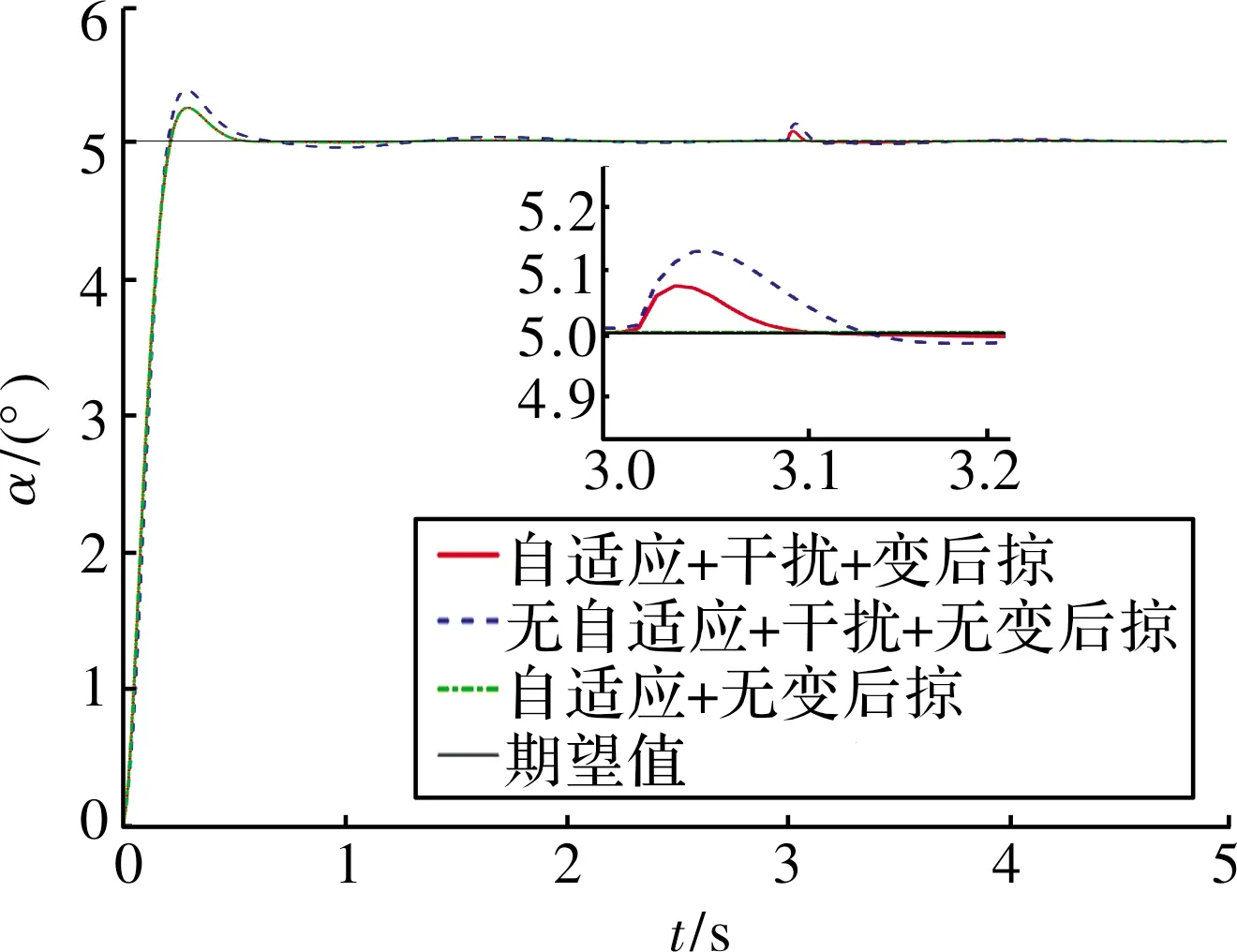
图8 攻角曲线

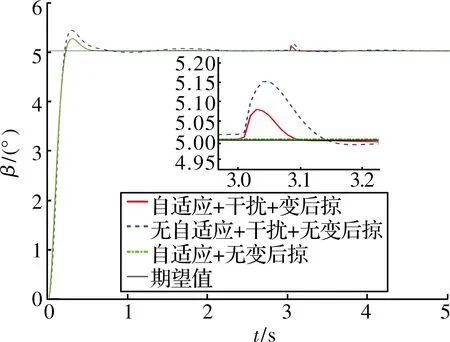
图9 侧滑角曲线

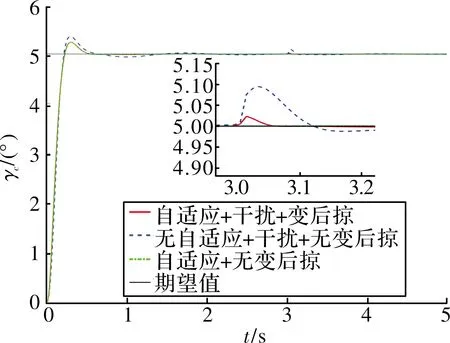
图10 倾侧角曲线

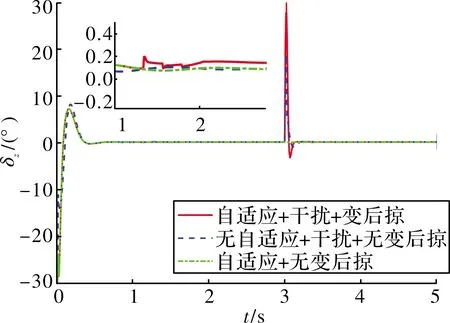
图11 副翼曲线

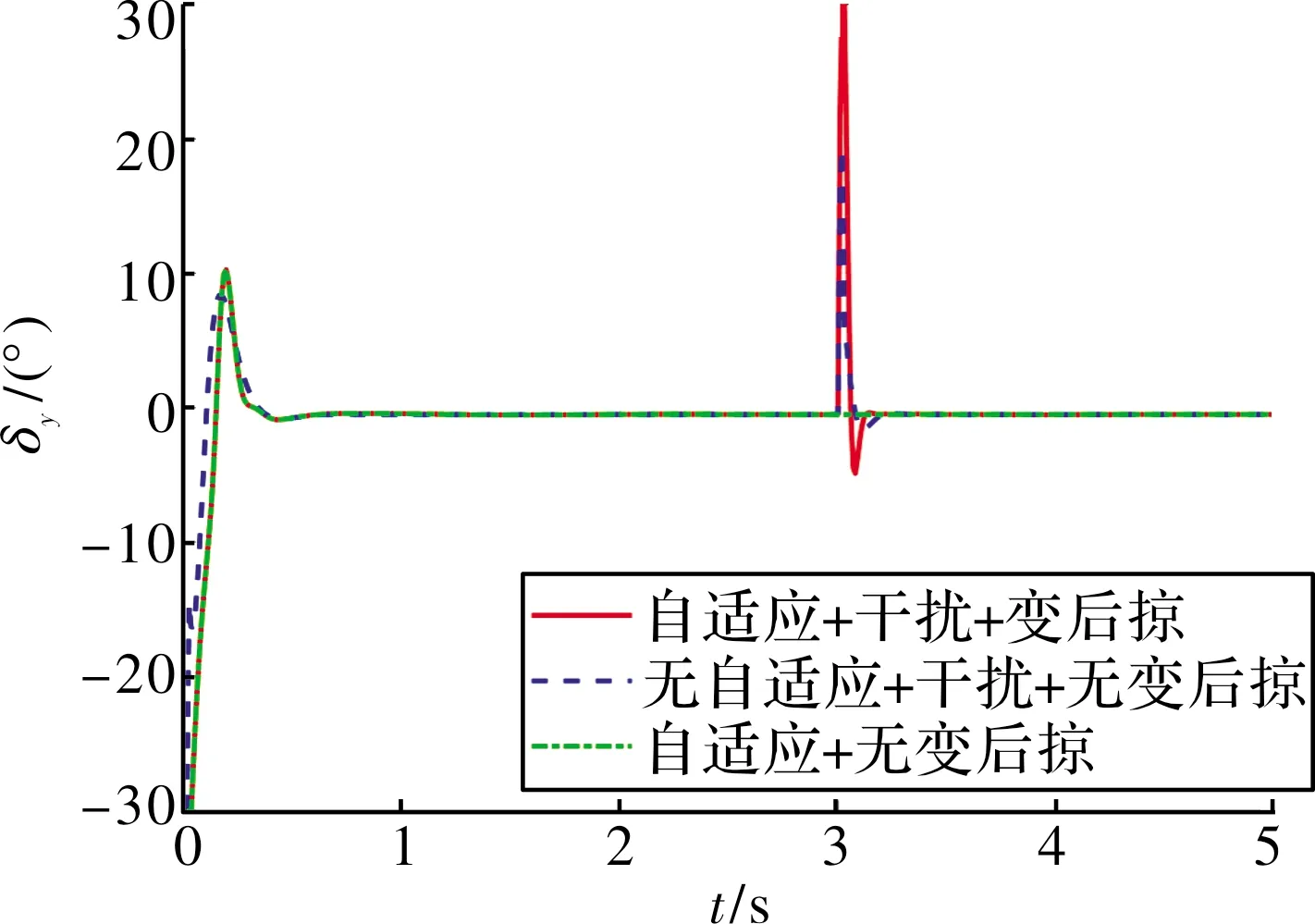
图12 方向舵曲线

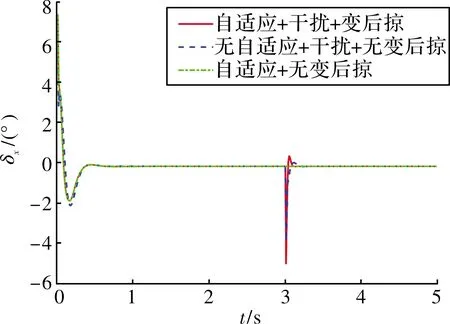
图13 升降舵曲线

5 结论

将PID参数作为神经网络隐藏层，利用梯度下降策略有效实现了变后掠翼飞行器在变形、受干扰情况下的参数自适应控制。采用基于神经网络的PID自适应动态逆控制方法，在响应时间、超调、对干扰的抑制程度以及舵资源的利用率上对于传统控制形式均有所提高。但该方法仍依赖于动态逆控制律，因此对于飞行器的精确建模具有较强的依赖性，后续会针对弱模型依赖的自适应动态逆控制问题开展研究。