通信访问约束条件下线性随机系统的可调节性研究

张 索

（浙江机电职业技术学院 电气电子工程学院，浙江 杭州 310053)

0 引言

在信道带宽资源受限的情况下，信道带宽无法承受系统所有数据的传输。若在某一固定时刻，需要同时传输的数据数量远远大于信道带宽所能传输的数据最大值时，就出现了通信访问约束的问题。在访问约束情况下，由于无法同时传输所有数据，故要在合理的通信策略下，决定所要传输的数据。而通信策略的选择会对系统的性质和性能产生影响，因此，有必要在通信受限的情况下，对系统的性能进行研究。

本文主要研究的是在输入约束情况下，线性随机系统的可调节性问题。本文通过该对偶关系，考察输入约束系统的可调节性问题。关于可估计性的定义，章辉等[1]从信息论的角度，提出了系统在最小最大误差熵（MMEE）意义下的可估计性定义，即状态的实际值和估计值的互信息大于零。本文也进一步证明了系统在MMEE意义下可估计性和可调节性之间的关系。理论分析和仿真结果表明，存在一个合理的静态通信策略，使得访问约束系统是可调节的。

1 问题描述

我们现要考察的是在输入约束条件下的线性时不变随机系统，如图1所示。

图1 输入约束条件下的线性时不变随机系统

2 输入约束系统的可调节性判别阵

Yoram Baram证明了系统在最小均方估计（LMSE）意义下可估计性和可调节性的对偶关系，提出线性系统的可估计性与可调节性是线性系统的两个对偶属性。该对偶性质可通过与系统的可估计性条件和可调节性条件，分别对应的Lyapunov方程和Riccati方程体现出来。Baram等[2]还证明了，系统的可调节性格莱姆矩阵和可估计性格莱姆矩阵具有对偶关系[2]。

因此，若系统∑是可调节的，即可调节性格莱姆矩阵WR满秩，则对偶系统∑'是可估计的（rankWR=rankWE=n）。我们把可估计性和可调节性的对偶关系用于输入约束系统∑ρ。只要找到输入约束系统（2）的对偶系统的可估计性判别矩阵，就可以找到它的可调节性判别矩阵。

3 MMEE意义下（最小最大误差熵）可估计性和可调节性的关系

这一部分要考虑在MMEE意义下，即在最小最大熵准则下，线性随机系统可估计性和可调节性的关系。

章辉等[1]给出了在最小最大误差熵（MMEE）准则下系统可估计性的定义：系统状态的实际值和估计值之间的互信息()大于零。章辉等[1]已经证明，对于线性高斯系统，MMEE意义下的最优估计等价于最小均方意义（LMSE）下的最优估计，如下式所示：

4 输入约束系统的可调节性分析

输入约束情况下的可调节性矩阵Λk'(i(n+1)+n,i(n+1))的值，相当于通信约束序列MρT(k)要从 Φkf,kTΠ'(k )B中挑选出wρ列。由于原系统的可调节性矩阵Λk(i(n+1)+n,i(n+1))是满秩的，故一定可从该可调节性矩阵中取出n个线性无关的列向量，设其为当i=0时，Λk(n，0)的n个线性无关向量集合为：

5 系统仿真

在输入约束条件wρ=1时，表示任意时刻从控制器到被控对象只能传输1个数据。其通信序列Mρ（k）表示为一个周期为3的通信序列：

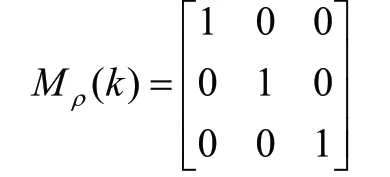
在输入约束条件wρ=2时，表示任意时刻从控制器到被控对象能传输2个数据。其通信序列Mρ（k）表示为：

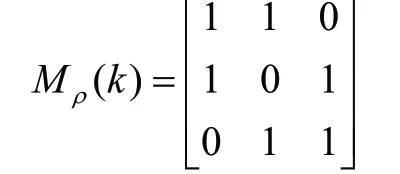
在这里，通过对偶系统的可估计性来考察该系统的可调节性问题。若对偶系统是可估计的，则原系统一定是可调节的。这里使用了Kalman滤波器估计出对偶系统的状态趋势。图1—2显示了系统的3个状态变量分别在通信约束条件wρ=1的情况下和wρ=2的情况下，状态变量的真实值和估计值之间的关系。其中，实线表示系统状态的实际值，点线表示系统状态的估计值。

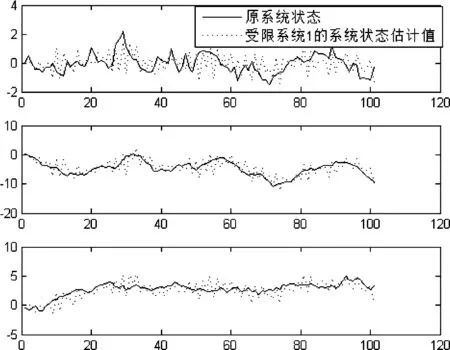
图1 输入约束条件1情况下系统状态的真实值与估计值

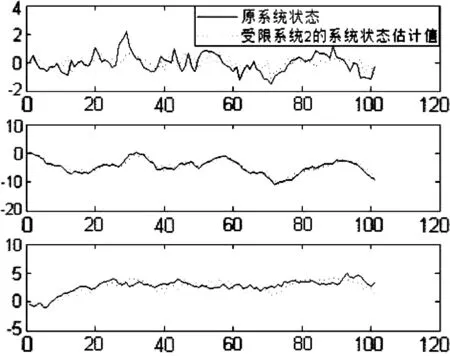
图2 输入约束条件2情况下系统状态的真实值与估计值

从图1—2可以看出，对偶系统的系统状态在有输出约束的情况下，仍然可以通过找到合适的通信策略，使得系统是可估计的。因此，也一定能通过合理的输出通信策略，使得原系统是可调节的。

以上仿真结果说明，对于输入约束系统，存在合理的通信策略，使得原系统是可调节的。

6 结语

本文针对输入约束情况下线性随机系统，研究了线性离散随机系统的可调节性问题以及系统的可估计性和可调节性之间的关系。仿真结果表明，在输入约束情况下，存在合理的通信策略，使得线性离散随机系统保持可调节性。