高斯矩阵测度集中不等式的相关证明

郑 珂，宋儒瑛

(太原师范学院 数学系,山西 晋中 030619)

0 引言

证明高斯随机测量矩阵满足RIP性质时，需要借助测度集中不等式的辅助.第一部分修正了高斯矩阵的测度集中不等式，在文献[1]中，这类不等式如下：

本文对这部分内容进行了修正，使得集中不等式的界改进的更加具体.

在实际应用中，测度集中不等式也有许多种，文献[2]中介绍了集中测量，其中包括随机矩阵的集中测量以及矩阵特征值的集中测量，文献[3]也有对矩阵特征值集中测量的介绍，文献[1]中第九章主要介绍了随机矩阵奇异值的集中测量，其中定理9.26证明了高斯随机测量矩阵奇异值的测度集中不等式，本文在这部分内容的基础上，继续对亚高斯随机矩阵奇异值的测度集中不等式，以及复高斯随机矩阵奇异值的测度集中不等式进行了证明，将这部分内容进行补充.

1 高斯矩阵测度集中不等式的修正

由于高斯随机矩阵是属于亚高斯随机矩阵的，亚高斯随机矩阵是属于一大类随机矩阵，其定义陈述如下：

定义1[1]设Y∈RN是一随机向量.

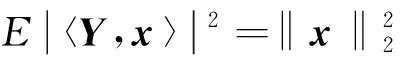
(b)若对于∀x∈RN并且‖x‖2=1，随机变量〈Y,x〉是亚高斯的并且高斯参数为c且独立于x，即，E[exp(θ〈Y,x〉)]≤exp(cθ2)，对于∀θ∈R,‖x‖2=1,那么Y表示亚高斯随机向量.

高斯矩阵的修正测度集中不等式陈述如下：

定理1设A∈Rm×N是高斯随机矩阵.对于∀x∈RN以及t∈(0,1)，

证明 设x∈RN.矩阵A∈Rm×N，不失一般性我们可以假设‖x‖2=1，我们用Y1,…,Ym∈RN表示矩阵A的列，并且考虑随机变量

因为Y是各向同性的，我们可得EZ=0.再者，Z是次指数的由于〈Y,x〉是高斯的，即亚高斯的，对于∀r>0，观察得当θ=1时，满足以下等式

根据次指数推导公式P(|Z|≥r)≤βexp(-kr)可知β=1,k=1，所以

通过Y的独立性，Z也是独立的.因此，对于次指数随机变量通过伯恩斯坦不等式[1][2][5]可以推导得

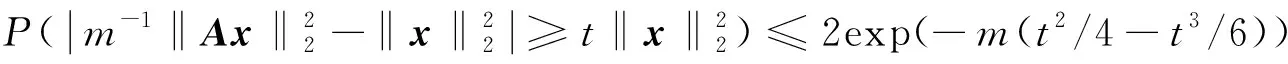
根据题设条件t∈(0,1)，与上述区间求交集可得当t∈(0,1)时，

结论显然成立.

2 亚高斯随机矩阵奇异值的测度集中不等式

在Simon Foucart和Holger Rauhut.研究的基础上，本节重点证明亚高斯矩阵奇异值的测度集中不等式，以及复高斯矩阵奇异值的测度集中不等式.

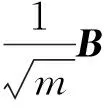
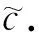
证明 证明时我们可以借鉴文献[1]中定理9.26的证明过程

首先引入亚高斯过程

文献[5]有对亚高斯随机过程的定义，其中g∈Rs,h∈Rm是两个独立亚高斯随机向量.

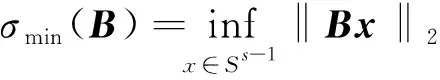
|σmin(A)-σmin(B)|≤‖A-B‖2→2≤‖A-B‖F.

见文献[2]中4.2节.根据文献[1]中定理9.21可知集中测量如下：

由于g∈Rs是亚高斯随机向量，那么向量中g=(g1,…,gs)∈Rs每个分量都服从亚高斯随机分布，即，g～Sub(c2),∈[s].见文献[6]中定理1.1以及[4]中(2.2)可得

由于h∈Rm是亚高斯随机向量，那么向量中h=(h1,…,hm)∈Rm每个分量都服从亚高斯随机分布，即，hi～Sub(1),i∈[m].

通过文献[1]中命题8.1(b)以及引理C.4，我们进一步可以得到

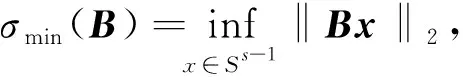
结果得证.

证明 对于复数矩阵这里我们需要对复数的运算进行一个简单的罗列

其中pj,qj,αj,βj都是独立零均值高斯随机变量，并且方差为1.

我们借鉴文献[1]中定理9.26的证明过程完成这个证明.

首先引入根据高斯过程

其中g∈Cs,h∈Cm都是两个标准高斯随机向量，g中每个元素为gj=pj+qji

g=p+qi,p=(p1,…,ps),q=(q1,…,qs),

h中每个元素为hi=αi+βii

h=α+βi,α=(α1,…,αm),β=(β1,…,βm),

pj(j=1,…,s),qj(j=1,…,s),αi(i=1,…,m),βj(j=1,…,m)

都是标准高斯随机变量.

接着根据文献[1]中(9.43)可得

P(σmax(A)≥E[σmax(A)]+r)≤e-r2/2

其中

那么上式转化为

同理，

P(σmin(A)≤E[σmin(A)]-r)≤e-r2/2

其中

由此带入到概率不等式中，可得

结果得证.

3 结束语

本文在文献[1]研究的基础上，对高斯随机矩阵测度集中不等式修正定理进行了证明，并且类比高斯随机矩阵测度集中不等式，补充并证明了亚高斯随机矩阵奇异值以及复高斯随机矩阵奇异值的测度集中不等式，使得压缩感知中涉及的随机矩阵测度集中不等式的研究更加完整.