基于超像素随机游走的自然场景图像分割方法

李 普，陈 黎,2

(1.武汉科技大学 计算机科学与技术学院，湖北 武汉 430065；2.智能信息处理与实时工业系统湖北省重点实验室，湖北 武汉 430065)

0 引 言

自然场景图像是目前人们通过各种成像设备获得的最常见的自然图像之一。随着成像设备、图像处理、计算机视觉等软硬件技术的发展，自然场景图像分析处理的学术价值和应用意义变得尤为重要。自然场景图像分割作为从低维度图像处理到高层自然场景图像理解的关键步骤[1]，占据着十分重要的地位，同时也是图像处理中最困难的问题之一。

近几十年来，针对图像分割这一问题，提出了各种方法，但大部分普遍缺乏普适性。所以，目前仍缺乏一种能够普遍适用于大多数应用场景或者能够自适应选择分割算法已得到当前应用下精确分割结果的系统。学者Leo Grady在研究交互式图像分割方法时将RW模型结合图理论知识应用到数字图像处理领域[2]。之后，该理论在多个图像处理领域获得成功应用，例如图像分割、图像滤波去噪[3]、图像检索及图像修复与增强等。随机游走图像分割作为一种半自动分割算法，加入少量的人为主观引导，并不能像无监督聚类算法一样自动完成整个分割过程，但却在一定程度上更有效地提取出目标区域[4]。因此，交互式的图像分割算法[5]在图像分割领域同样拥有很高的研究意义和应用价值。

作为一种交互式的分割模型，RW图像分割算法虽然不能全自动完成整个分割过程，但相比于其他方法具有十分明显的优势：(1)拥有完备的数学理论基础支持算法的可用性。(2)通过将图论结合到数字图像中，通过求取带权边的概率最大化问题解决图像分割问题，直观性和可计算性强。

但是，由于随机游走模型本身的特殊性，它在处理自然场景图像的过程中还存在以下几点问题：(1)随机游走过程是以像素为基本计算单位进行的，处理大尺寸图像时耗时过长。在实际应用中，随着图像采集技术的发展，图像分辨率大幅提升，提升大尺寸图像的分割效率越来越重要。(2)仅利用像素灰度值引导随机游走的方向，没有充分利用颜色、空间纹理等特征，对纹理复杂的图像不能实现较好的分割效果。

超像素是一类具有相似度量的像素集合。它为计算局部图像特征提供了方便，大幅降低了后续图像处理的复杂性[6-7]。SLIC(simple liner iterative clustering)[8]是一种运用简单线性迭代聚类的超像素分割算法，该算法可获得形状规则、大小均匀的超像素分割结果[9]，而且在运算速度、物体轮廓保持等方面相比于其他超像素分割算法有比较良好的表现。针对传统随机游走算法处理自然场景图像时，存在分割效果不精确、效率低的问题，该文提出基于超像素改进的随机游走图像分割算法。

1 随机游走图像分割算法

随机游走图像分割算法是建立在图论的基础之上，图论是数学知识的一个分支，已成为其他应用领域一个重要的理论工具，而图论的基石是图。图是四类基本逻辑结构中最为复杂的一种，它将事物之间的联系以直观化、结构化的形式表现出来，在图的结构中，任意两个节点之间都可能相关。图结构由节点集V和代表节点间关系的集合E组成，表示为G=(V,E)。V代表图结构中节点的集合(点集)，E代表图结构中相邻节点之间关系的集合(边集)[10-11]。

数字图像实质上是像素点矩阵，图结构中的节点集合V就代表了图像中的像素，相邻的像素连接起来就构成带权值的边，所有的带权边组成了图结构中的边集E[12]。带权边描述了相邻节点之间的相似程度，决定了随机游走过程中下一步游走的方向。

随机游走图像分割算法的基本思想就是首先通过原始图像构建一个无向加权图。人为标记的像素点作为种子点，然后通过无向加权图计算非种子点到达种子点的概率，通过比较将非种子点像素划分到对应最大概率种子点的所属区域，得到最后的分割结果。

1.1 边的权值

构建的无向加权图用G=(V,E)来表示。其中，节点v∈V表示原始图像的像素点，e∈E⊆V×V表示原始图像中像素连接邻域像素的带权边。边eij的权重wij∈W表示节点以该边移动的可能性大小，无向边的权重值由高斯函数得到：

wij=e-β(gi-gj)2,∀eij∈E

(1)

式中，gi,gj代表像素点vi,vj的强度，β是一个可控的参数。边的权值直接引导随机游走的下一步方向，因此权值函数构建方式会对随机游走的分割结果产生直接的影响。目前为止，大量理论和实验表明通过高斯核函数构建权值的效果比较理想。

1.2 求解狄利克雷问题

计算随机游走节点的归属概率值的过程与已知边界条件情况下求解Dirichlet是等价的，所以非种子点的归属计算问题，就可以转化为求解在0和1为边界条件下的联合Dirichlet问题[13]。

狄利克雷积分为：

(2)

式中，Ω表示积分区域，u表示场[14]。

式(3)为调和函数，它满足拉普拉斯方程，边界条件Γ为式(4)[15]，满足边界条件Γ的调和函数问题可以使得式(2)取得最小值，而寻找该函数则称为狄利克雷问题。Laplace方程则是求解狄利克雷的欧拉-拉格朗日方程。

(3)

(4)

为了求解该问题，先定义组合拉普拉斯矩阵Lij。

(5)

式中，Lij为vi和vj的关联矩阵，di=∑wij为vi的度。

然后定义关联矩阵A，来描述所有节点之间的关联关系。

(6)

式中，通过边e和节点v共同决定关联矩阵A的值。矩阵A为联合梯度算子，AT为散度算子。

C为大小m×m的对角矩阵，用来表示图结构中的边的权值，如式(7)。

(7)

此时，得到一个Laplacian算子L。C为一个调节矩阵乘积的因子。

L=ATCA

(8)

因此，式(2)便可以表示为关于图结构中边、点及权重三大要素的新形式，见式(9)。

(9)

将G中的顶点V由两部分组成，标记的种子点集合VM以及没有被标记的节点集合VU，两者的关系可以用VM∪VU=V,VM∩VU=∅表示，将拉普拉斯矩阵按照是否为标记点进行重新组合，如式(10)。于是，式(9)可以分解成式(11)。

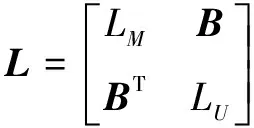
(10)

(11)

其中，LM、LU分别表示种子点及非种子点集合构成的拉普拉斯算子，xM和xU表示标记点和未被标记点的能量值。

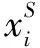
(12)

因此，通过式(13)，可以求取非种子点与某一个标记为s种子点的联合Dirichlet的解。狄利克雷问题可以通过电路图的形式来进行分析，而在电路图中，所有节点的电势值之和为1。因此，在图结构中非种子点游走到种子点的概率之和也为1，如式(14)所示。那么可以利用式(15)计算出所有未标记节点第一次移动到已标记节点的概率。

Luxs=-BTms

(13)

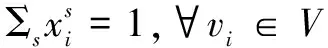
(14)

LUX=-BTM

(15)

通过以上过程，计算出所有非种子节点VU分别游走到各个种子点VM的概率。然后将所有节点划入概率最大的种子点所属范围内，最终将图像所有的像素点进行分类，类别数与事先标记种子点的类别数相同，实现图像分割[16]。

2 基于超像素的RW图像分割方法

利用超像素边界贴合度好及通过将像素区域化降低计算量等优点，对传统的随机游走图像分割方法进行改进。基本思想是：第一步通过超像素分割算法对原始图像作区域化处理，生成若干个超像素块。利用生成的超像素替代单个像素称为新的节点，然后提取超像素区域颜色直方图及区域纹理信息联合组成高斯权值函数，构建无向加权图，最后在新构建的无向加权图上进行随机游走实现分割。

2.1 SLIC超像素分割

超像素是由一系列位置相邻且颜色、亮度、纹理等特征相似的像素点组成的像素块。它通过将局部像素聚合在一起，为计算图像局部特征提供了便利，同时大幅降低了后续图像处理的复杂性[17]。该文采用一种简单线性迭代聚类的超像素分割方法(SLIC)。

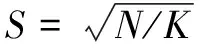
由于每个像素的五维特征向量包含了两种不同的含义，一种是像素的颜色，一种是像素的空间距离。所以可以适当地对空间距离这一部分进行加权，以平衡它们在聚类过程中的影响，其公式如下：

(16)

(17)

(18)

其中，Ds是度量值；参数m为用来调节超像素的紧致度，m越大，那么空间相似性权重则越大，聚类结果越紧密。该文以m=10作为参数；lk、ak、bk分别表示第k个超像素区域中心像素点的lab值，li、ai、bi则表示在2S×2S区域内像素点i的lab值；xk、yk表示第k个超像素区域中心像素点的图像坐标值，xi、yi则表示在2S×2S区域内的像素点i的图像坐标值；dlab表示第k个超像素区域中心像素点与其周围2S×2S区域内的像素点lab颜色空间的距离度量值；dxy表示第k个超像素区域中心像素点与其周围2S×2S区域内的像素点图像坐标的欧氏距离度量值。

2.2 RW权值的改进

传统随机游走图像分割算法的最小计算单位是单个像素，利用像素的灰度值特征得到边的权值。而在基于超像素改进的随机游走图像分割方法中，节点从单个像素变为超像素。因此，计算两个超像素块相似性的方法也发生了改变。该文提出提取超像素的颜色直方图以及区域性LBP纹理信息来共同构建权值函数，作为两个超像素块的相似性度量。

(1)颜色直方图。彩色图像由三个颜色通道组成，分别包含256个颜色度量值。为了尽量保留原始图像的颜色信息，同时提高算法效率，将三个通道分别都划分为16个颜色分组。因此，三通道信息可以产生4 096个颜色信息值。公式(19)为通过4 096个特征值来描述两个超像素颜色差异度的颜色直方图欧氏距离d(M,N)。

(19)

其中，HM和HN分别表示超像素M和N的归一化颜色直方图。d(M,N)越大则表示两超像素区域之间的颜色距离越大，这两个超像素块在颜色空间上的差异性越大。反之，则两个超像素近似程度越高。

(2)LBP纹理特征。LBP特征是一种用于描述图像纹理的局部特征。仅仅依靠颜色直方图来评判超像素区域之间的相似度容易造成分割结果不准确，因此加入超像素区域性LBP纹理信息。图像中以c为中心像素点，p点邻域中的LBP纹理值定义为：

(20)

(21)

式中，gc,gp分别为中心点c及c的p邻域点的灰度值。

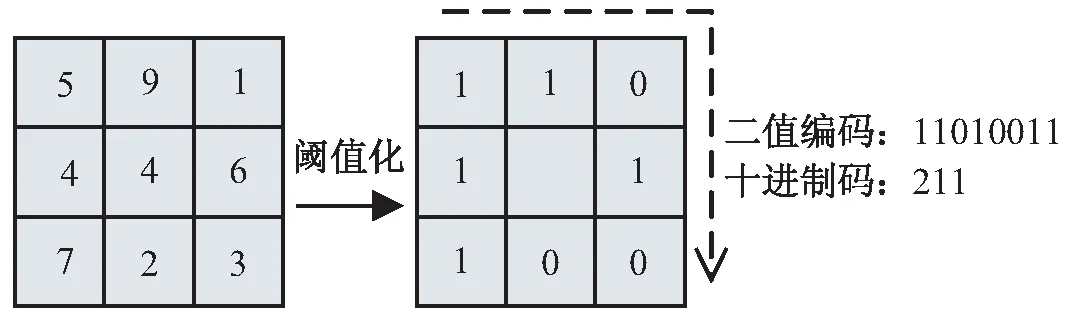
图1 LBP特征计算示意图

利用式(22)表示超像素D中,n个像素点的平均LBP纹理值。

(22)

用LBP纹理值的欧氏距离来表示超像素M和N的纹理信息差异度，见式(23)。

(23)

(3)改进后的权值。该文将上述两种欧氏距离与高斯函数联合起来共同构建权值函数w。这样能够更加准确地描述两个超像素区域之间的相似程度。超像素M、N之间的权值定义为：

wM,N=exp{-β1d(M-N)2-β2e(M-N)2}

(24)

式中,β1，β2>0为两个可调参数，决定两种特征的影响度。

3 实验结果与分析

该文主要安排对比实验，验证基于超像素改进的随机游走图像分割算法的有效性和相比于传统随机游走图像分割算法的优越性。实验数据取自BSDS500分割数据集。本实验所用的实验环境为：MATLAB R2014B；实验硬件条件为戴尔笔记本(CPU：Intel(R)Core(TM)i5-7300HQ CPU @ 2.50 GHz;内存：12 GB；操作系统：64位Windows10)。

3.1 定性分析

实验一：针对该文提出方法的有效性，本实验选取两张分辨率分别为585*373和480*320的简单图像，分别使用传统RW图像分割算法和基于超像素改进的算法来对图像进行分割。实验结果表明，对于前背景颜色简单、纹理信息差异明显的图像，基于超像素改进的算法与传统的RW图像分割算法都能比较理想地分割出目标。图2为实验中的两组实验结果，对分割结果作二值化处理以进行对比分析。

图2 不同算法图像分割效果

实验二：本实验针对基于超像素改进的RW图像分割算法相对于传统RW图像分割算法的优越性，下面是本实验选取的纹理结构相对较复杂的图像(见图3)，分辨率分别为690*445、1 280*840和960*596。通过直观地对比实验结果，可以明显观察到，基于超像素改进后的RW算法得到的分割结果更加贴近真实目标。

图3 不同算法分割效果

由以上实验结果可以看到，传统的RW算法在处理自然场景中颜色及纹理信息丰富的图像会存在过分割和欠分割的情况。而基于超像素改进的RW图像分割算法，对自然场景中复杂图像的处理能力上有明显提升。其中，对鹿的实验结果中在鹿腿和鹿角上的分割效果最为明显。

3.2 定量分析

本节将对算法的分割结果与人工分割结果进行量化分析，并对算法的效率作对比分析。

图像分割结果的量化对比以重合率PO和误差率PM作为判别标准,其定义如下：

(25)

(26)

式(25)、(26)中S表示人工标准分割结果，SC为算法实现的处理结果。式(25)中TO表示以人工分割为标准的前景目标部分，O表示算法分割结果与人工标准分割的前景目标重叠部分。式(26)中MC为算法分割结果中的误差部分。其中：

(27)

(28)

表1为分割结果精确度量化数据。由实验结果和表中数据可知，对于以上五幅图像，基于超像素改进的随机游走图像分割方法均能比较完整地分割出前景目标。在前两幅图像中，前背景颜色和纹理信息相对简单，传统的RW图像分割算法和基于超像素改进的RW图像分割算法均能得到理想的目标分割边界。对于实验二中的三幅图像，基于超像素改进后的算法能够得到更贴合真实目标的分割边界，实现更好的分割效果。

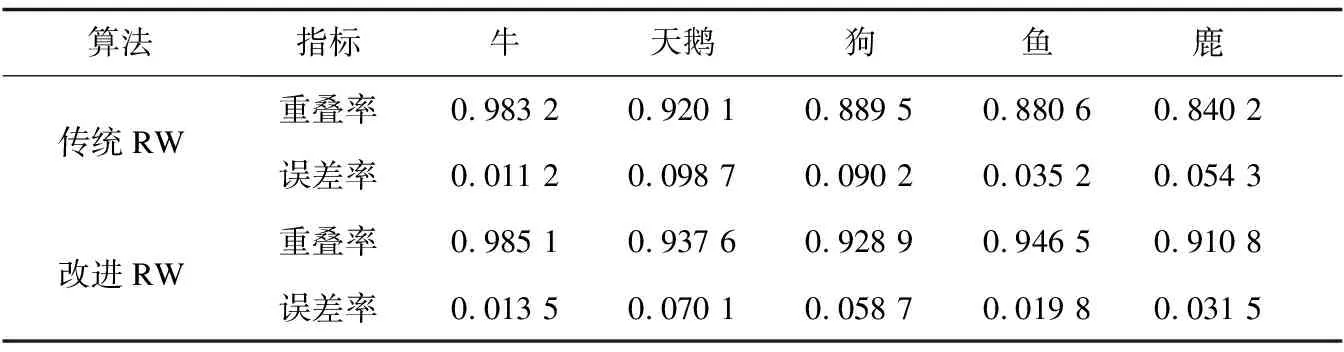
表1 不同算法分割结果精确度量化对比

表2为以上两个实验中的图像的分割效率。由表中数据对比可知，基于超像素随机游走图像分割算法在计算效率上有了明显的提高。

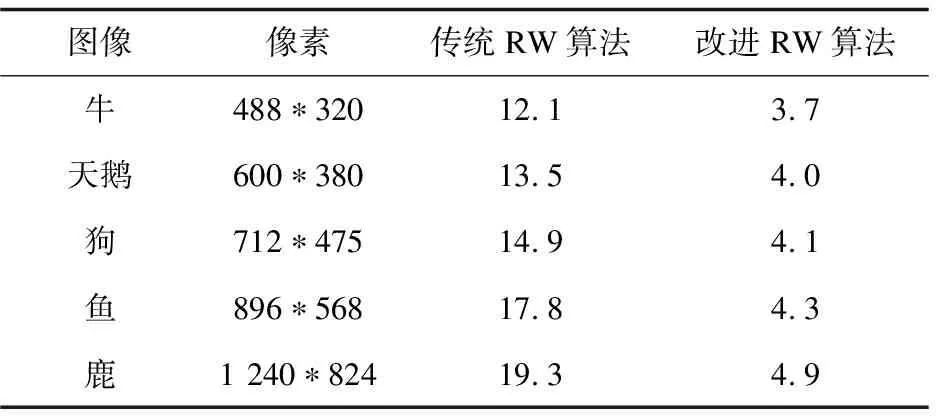
表2 不同算法分割效率对比 s

4 结束语

针对传统随机游走图像分割算法在处理自然场景中前背景颜色纹理信息相对复杂、分辨率大的图像时，存在目标边界难以贴合甚至分割错误以及效率较低的问题，提出基于超像素随机游走的自然场景图像分割方法。通过超像素预处理将原始图像离散化为若干个尺寸相对均匀的超像素区域，然后以超像素区域的颜色直方图和区域性纹理信息衡量两个超像素的相似性。以超像素替代原始像素作为图结构中的节点，超像素之间的相似度作为边的权值构建新的无向加权图，最后在新构建的无向加权图上进行随机游走实现分割。该方法可以在一定程度上提高精度和效率。由于该算法的分割结果是通过对超像素进行合并处理得到的，所以会造成分割结果边缘不平整的问题，针对这一现象后续有待进一步研究。