基于PT 对称的亚波长谐振耦合超灵敏传感

车衍子亦 廖志斌 彭星 廖臻，3

（1. 杭州电子科技大学, 杭州 310000；2. 新余学院, 新余 338000；3. 毫米波国家重点实验室, 南京 210096）

引 言

长期以来，传感技术一直是许多行业如医疗、民用、航空等的主要需求，其需要对目标的物理参数进行高精度的测量，尽管传统的光学方法也可以实现这一目的，但这些技术通常是复杂且昂贵的. 因此这成为研究人员亟待解决的难题. 1967 年科学家设计出了第一个采用螺旋式电感和压力感应式电容的无线传感器，可用来测量眼内液压[1]. 随着无线技术和纳米技术的发展[2-4]，基于无源器件的传感器被广泛应用于测量压力、温度、距离等. 最近基于亚波长结构的传感应用[5-7]也得到人们的重视及研究，有望在健康检测、生化分析、环境监测等领域得到应用[8-9].虽然这些传感应用能对周围环境的变化做出一定频率响应，但对于极小的环境改变所产生的频率变化也极小，很难进行分辨. 如何实现超灵敏度的传感依旧是研究人员需要去解决的难题.

在此次工作中，我们设计了一种新的基于PT 对称的亚波长谐振耦合系统. 其中谐振结构是以螺旋形开槽的金属结构为基础，通过在每个金属臂上加载电阻，将损耗引入系统构建耦合系统，令整个系统符合PT 对称，并通过调整两个谐振单元之间的耦合系数，达到系统的EP. 当耦合系统中两个谐振单元发生轻微位移时，系统会出现微扰离开EP，并产生较大频率分裂. 本文从理论、仿真和实验三个方面与传统耦合系统进行了比较，证实了本文PT 对称系统对极小位移具有更高的灵敏度.

1 PT 对称耦合系统分析

双分耦合系统是常用的PT 对称系统，该系统的耦合方程可以写为[19-20]：

2 金属螺旋谐振结构

图2(a) 给出了金属螺旋谐振结构的正面示意图，该结构由三个螺旋金属臂组合构成，在每条臂上加载一个电阻. 金属结构覆盖在40 mm×40 mm×1.5 mm的聚四氟乙烯介质基板上，基板的介电常数为2.5.螺旋金属结构的具体尺寸如下：宽度w为2 mm，外半径R为14 mm，内半径r1为3 mm，臂间距g为1.67 mm，厚度为0.035 mm. 如图2(b)所示，介质基板的背面为谐振单元的馈电结构. 谐振单元采用共面波导馈电，馈线长度L为20 mm，共面波导缝隙s为0.1 mm，馈线末端接半径r2为1.5 mm 的圆形枝节.

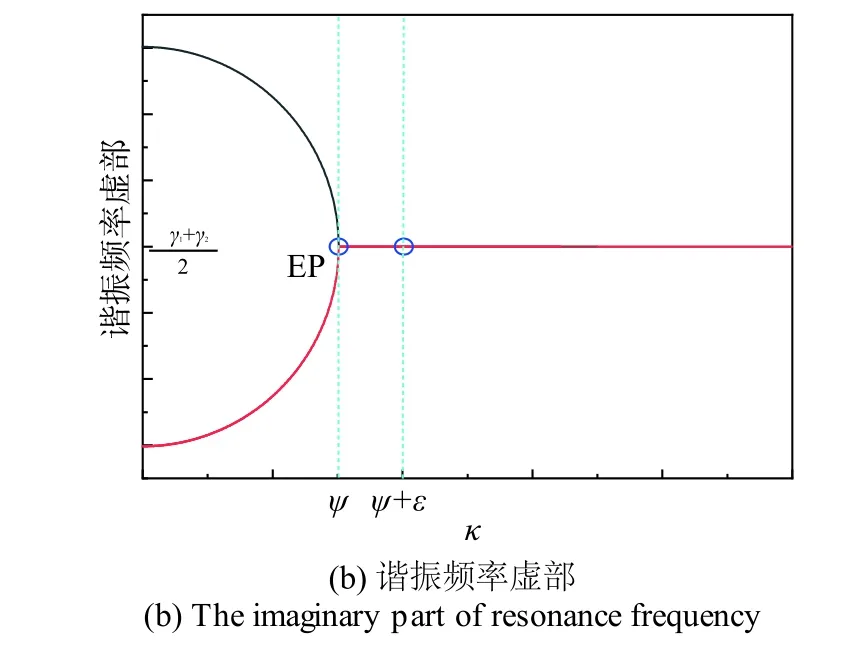
图1 谐振频率与耦合系数的关系Fig. 1 Relation between resonance frequency and coupled coefficient

图2 金属螺旋结构Fig. 2 Metallic spiral structure

利用商业仿真软件CST 对加载不同电阻时的频率响应进行全波仿真，其反射系数如图3 所示. 仿真结果表明该结构在1.76 GHz 时，形成了一个明显谐振峰，波长约为110 mm. 而金属螺旋结构相当于0.13 个波长，属于亚波长结构. 随着加载电阻的阻值从0 Ω 到40 Ω 变化，谐振峰频点保持不变，而相应的线宽逐渐变大，表示谐振频率的实部不变，虚部逐渐增大. 为进一步明确电阻与虚部的关系，利用洛伦兹模型对反射系数进行拟合，得到电阻与谐振频率虚部的关系，如图4 所示. 可以看出，通过在谐振单元中引入电阻，能够有效控制谐振频率的虚部. 而谐振频率的实部主要由金属螺旋结构决定[21].

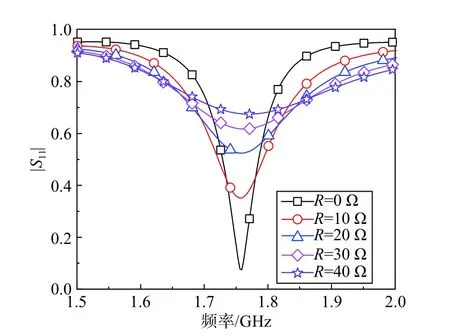
图3 不同阻值下的反射系数仿真结果Fig. 3 Simulated reflection coefficient of different R

图4 电阻与谐振频率虚部的关系Fig. 4 Relation between resistance and the imaginary part of resonance frequency

3 PT 对称的金属螺旋谐振系统

为提高金属螺旋谐振系统的传感特性，构建PT 对称的谐振耦合系统，如图5 所示. 将两个金属螺旋谐振结构水平放置，结构之间的垂直距离h为7 mm，利用两个谐振单元之间的耦合，构建成一个双组分的耦合系统. 同时，在谐振单元中引入电阻，实现复数的谐振频率. 通过改变两个谐振单元之间的水平距离 ΔX，能够改变系统的耦合系数，从而使得系统达到EP.

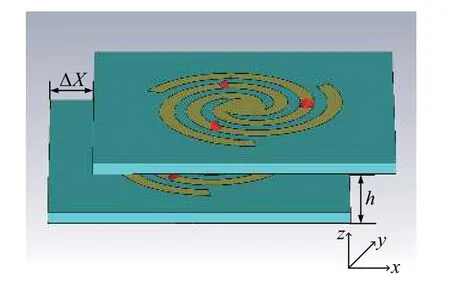
图5 PT 对称耦合系统示意图Fig. 5 Schematic of PT-symmetric coupled system

首先确定了两个谐振单元中加载电阻的阻值分别为0 Ω 和20 Ω. 为达到系统的EP，逐渐增加水平位移ΔX以达到调整耦合系数的目的. 通过仿真，图6 给出了耦合系统的反射系数与水平位移量 ΔX的关系. 可以看到：在 ΔX小于14 mm 时，耦合系统的反射系数有两个谐振频点，说明此时整个系统有两个本征频率；当 ΔX达到14 mm 时，反射系数中只出现一个谐振峰，说明此时系统的本征频率发生了简并.基于前面理论分析可知， ΔX= 14 mm 时整个系统达到EP.

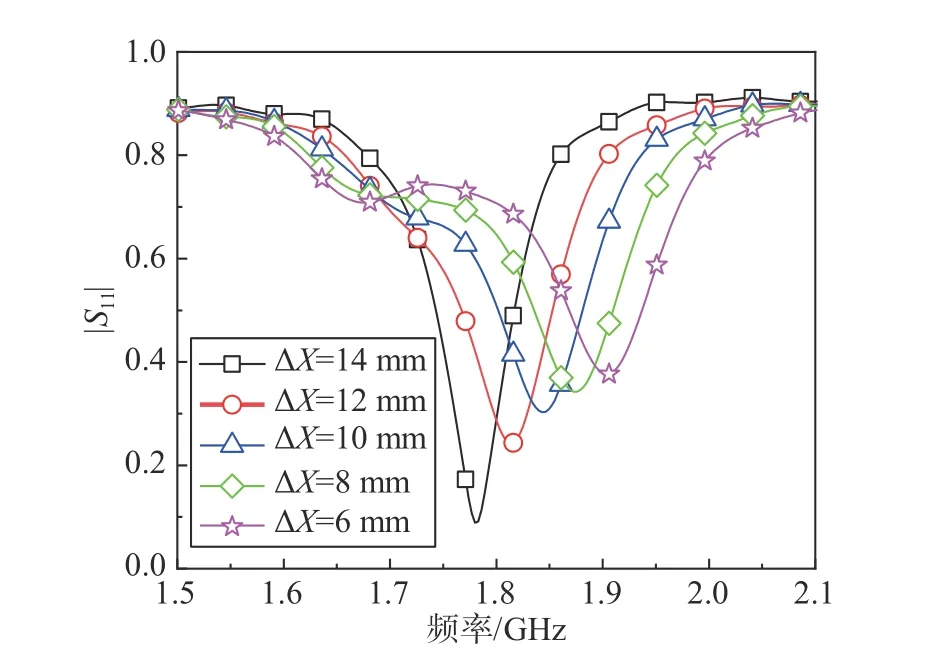
图6 PT 对称耦合系统不同 ΔX 下的反射系数Fig. 6 Different reflection coefficients ΔX of PT symmetry in coupled system

为进一步验证PT 对称的金属螺旋谐振系统在EP 附近的超高灵敏度，比较了PT 对称耦合系统和传统耦合系统对EP 附近微扰的频率响应. 图7 为PT 对称耦合系统实物图，图8 为传统耦合系统示意图，图9 和图10 分别给出了PT 对称和传统耦合系统的仿真实验反射系数. 由于加工、SMA 头及实际测试会造成一些误差，导致实测结果和仿真有些偏差. 图9 和图10 中蓝色阴影部分为不同位移情况下的频率变化量. 结果表明当水平位移从14 mm 变为6 mm时即谐振结构自EP 处移动8 mm(约0.05 波长)，PT对称系统的频率分裂变化量为0.25 GHz，而传统耦合系统的频率分裂变化量为0.164 GHz，实验结果与仿真结果一致，证明了PT 对称的金属螺旋耦合系统比传统的耦合系统具有更高的灵敏度.

图7 PT 对称耦合系统实物图Fig. 7 Prototype of the proposed PT symmetry of coupled system

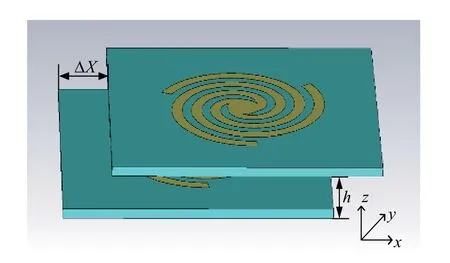
图8 传统耦合系统示意图Fig. 8 Schematic of the traditional coupled system

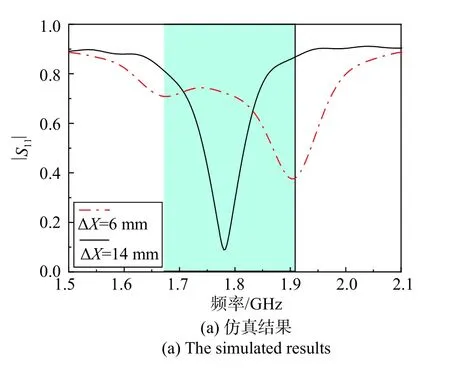
图9 PT 对称耦合系统反射系数变化Fig. 9 Variation of reflection coefficient of PT symmetry in coupled system

图10 传统耦合系统反射系数变化Fig. 10 Variation of reflection coefficient in traditional coupled system

4 结 论

本文提出了一种基于PT 对称的亚波长谐振耦合超灵敏传感系统，其中谐振结构是以螺旋形开槽的金属结构为基础，通过在每个金属臂上加载电阻，引入复数的谐振频率; 通过水平位移调整两个谐振单元之间的耦合系数，实现PT 对称并达到系统EP.在EP 处发生极小位移时，PT 对称系统产生了较大的频率变化. 该系统在建筑、医疗及探测等领域具有较大的应用前景.