基于超表面的智能电磁感知：理论、系统与实验

双雅 李力 王卓 魏梦麟 李廉林

（1. 北京大学信息科学技术学院，北京 100871；2. 北京航天测控技术有限公司，北京 100871）

引 言

电磁感知具有穿透性、非接触性和非电离性等特点，在安检[1]、医学成像[2]、手势识别[3]、资源勘探[4]等科学、工程和军事领域已成为一种不可或缺的探测技术. 迄今为止，电磁感知系统主要有三种被广泛应用的体制：合成孔径(synthetic aperture SA)体制[5]、实孔径(real aperture, RA)体制[6-7]和基于编码孔径的计算成像体制[8-16]. RA 系统是由大量的天线单元组成大口径阵列，其在测量方式上非常灵活，但对收发组件要求苛刻，导致系统成本居高不下. SA 系统由于依赖单个传感器的机械扫描导致其在数据采集方面存在较高的时延，同时面临数据后处理耗时的问题. 在压缩感知理论的启发下[17]，基于编码孔径的计算成像系统在过去十年中得到了广泛研究，特别是在解决SA 系统和RA 系统引入的极具挑战性的问题方面取得了重要的飞跃[8-16]. 这些技术背后的工作原理是在数据采集过程中，通过信息压缩技术将数据处理的负担从硬件转移到软件. 尽管这些技术能够从非常少的测量数据中获取场景的信息，感知系统仍然亟需引入更加“智能”的方法. 因为在上述技术中，即使被探测的一系列感兴趣场景具有共同的特征，电磁感知系统仍然会无差别地获取每个场景的所有信息，而且每次得到的逆散射问题都需要通过耗时的迭代算法进行重复求解. 因此，在探测场景时对具有共同特征的场景进行自适应的数据采集和快速提取特征是非常有必要的[11,18].

最近，科研工作者将人工智能技术(本文指深度学习)和人工电磁材料(本文特指可编程超表面)集成为一个整体，实现了智能电磁感知技术[19-20]. 可编程超表面[21-23]是一种由大量电可调控单元构成的超薄平面型阵列，它能够任意、动态地调控电磁波前，目前在电磁感知[24-25]和无线通信[26-27]领域中有着重要的应用价值. 相比传统的相控阵系统，可编程超表面具有更加简单的结构和更低的硬件成本. 而深度学习具有强大的信息处理能力，能够实现实时的数据处理，极大地提高了电磁感知系统的性能和效率.

本文从理论、系统设计和实验的角度深入研究了基于深度学习和可编程超表面的智能感知方法，如图1 所示. “智能”指在数据处理过程中引入深度学习技术，提取被探测场景的共同特征，实现更高效率的数据处理. 本文的具体工作安排如下：第一部分从“k 空间”的角度分析了基于可编程超表面的电磁感知系统的自身成像分辨率，并分析了影响成像分辨率的系统因素. 第二部分介绍了一款大规模1 比特反射型可编程超表面，并通过实验验证了其灵活调控电磁波前的良好性能. 第三部将深度学习技术引入电磁感知系统的数据处理层，实现了在现实环境中的智能成像，并依据图像质量和测量次数两个指标讨论了系统的成像性能. 最后，第四部分对本文进行了分析总结.

图1 基于超表面的智能感知系统框图Fig. 1 Schematic of metasurface-assisted intelligent sensing scheme

1 电磁感知系统的分辨率分析

本节利用k 空间分析方法从理论上研究了基于可编程超表面的电磁感知系统在没有使用高级的数据后处理算法的前提下，其自身的成像分辨率. k 空间，也被称为Ewald 球和角谱，是一种用来粗略估计感知系统成像分辨率的有用工具[28-29]，描述了待探测场景的三维(3D)空间频谱分布.

图2 为基于可编程超表面的电磁感知系统示意图. 其中，可编程超表面通过切换不同的照明模式来探测感兴趣的场景，单一的接收天线接收从场景散射的回波. 根据k 空间的定义可知，电磁感知系统的成像分辨率取决于被探测目标在k 空间的填充面积.更具体地说，横向分辨率 δx和 δy分别由kx和ky方向上的填充域确定，而距离分辨率则由kz方向上的填充域决定. 三个方向上的成像分辨率的数学表达式由文献[28-29]给出：

图2 基于超表面的电磁感知系统示意图Fig. 2 Schematic configuration of electromag netic metasurface-assisted sensing system

图3(a)绘制了当可编程超表面和被测目标之间的距离D从 4λ增加到25λ(步长为 λ)时，三个方向上成像分辨率δx,y,z的变化趋势；图3(b) 给出了当D=10λ时，成像分辨率随可编程超表面尺寸Lx,y增加的变化趋势. 这里默认可编程超表面在x和y方向上的尺寸相同. 显然，随着距离D的增大，三个方向上的成像分辨率降低；而随着可编程超表面尺寸Lx,y的增大，成像分辨率增强. 这些结果可以通过式(2)进行验证.

图3 目标与超表面的距离D 和超表面的尺寸Lx,y 对成像分辨率δx,y,z的影响Fig. 3 Impacts of distances between targets and metasurface Lx,y and size of metasurface D on the imaging resolutions δx,y,z

图4 给出了当可编程超表面和被测目标之间的距离D增大时，目标在kxoky、kxokz和kyokz平面内的空间频谱分布，默认系统的工作频率f=2.5 GHz. 第一列到第三列分别描述kxoky、kxokz和kyokz平面中的空间谱分布，第四列给出了三维空间谱分布. 灰色圆的半径是k0，k0表示自由空间中的波数. 图4 进一步说明成像系统的分辨率与k 空间的填充区域面积成反比.

图4 当可编程超表面和被测目标之间的距离D 增大时目标在k 空间内的空间频谱分布Fig. 4 Spatial spectrum distributions in the k-space for the case of increasing distance D between metasurface and imaged object

类似于图4 的结论，随着可编程超表面尺寸的增加，目标在k 空间的填充区域面积同样减小. 此外，由式(2)可知：当被测目标无限接近可编程超表面时， δx和 δy逐渐趋向于λmin/2；相反，当物体逐渐远离可编程超表面时，横向分辨率 δx和 δy将收敛于λminD/Lx,y，距离分辨率 δz趋向于c/(2Δf). 这一结论与经典雷达系统中的结论是一致的[30]. 上述研究表明，在不引入分辨率增强的数据处理算法时，电磁感知系统的成像分辨率受到衍射极限的限制.

2 可编程超表面系统

本节介绍了32×24 单元的1 比特反射型可编程超表面系统，并通过实验验证了其在电磁物理层面调控电磁波前的优越性能.

2.1 可编程超表面设计

本文所使用的可编程超表面来源于文献[25]，它由32×24 个电可控的1 比特单元组成，中心工作频率为2.43 GHz. 超表面单元的几何结构如图5(a)所示，单元上层由一个正方形贴片和一个90°弯曲的金属条带组成，介质采用厚度1.5 mm 的F4BM 基板，介电常数εr=2.65. PIN 二极管(SMP1345-079LF)将方形贴片与90°弯曲的金属条连接起来，在贴片的另一侧设计一条偏置线为二极管馈电. 所有结构参数如图5(a)所示. 根据该单元结构，本文利用PCB 技术制作了32×24 可编程超表面样机[25].

如图5(b)所示，本文采用空间波法验证制作的可编程超表面的性能. 测量结果如图5(c)所示. 结果表明，当可编程超表面所有PIN 二极管在开和关两种状态之间同时切换时，可编程超表面将在2.43 GHz产生180°的相位差. 此外，为了灵活调控可编程超表面的编码序列，本文设计了基于FPGA 的控制板来任意控制PIN 二极管的开关状态，该控制板仅利用一块FPGA 芯片向所有的PIN 二极管发送状态控制信号. 控制板的时钟频率为50 MHz，理论上PIN 二极管的开关时间可以达到10 μs.

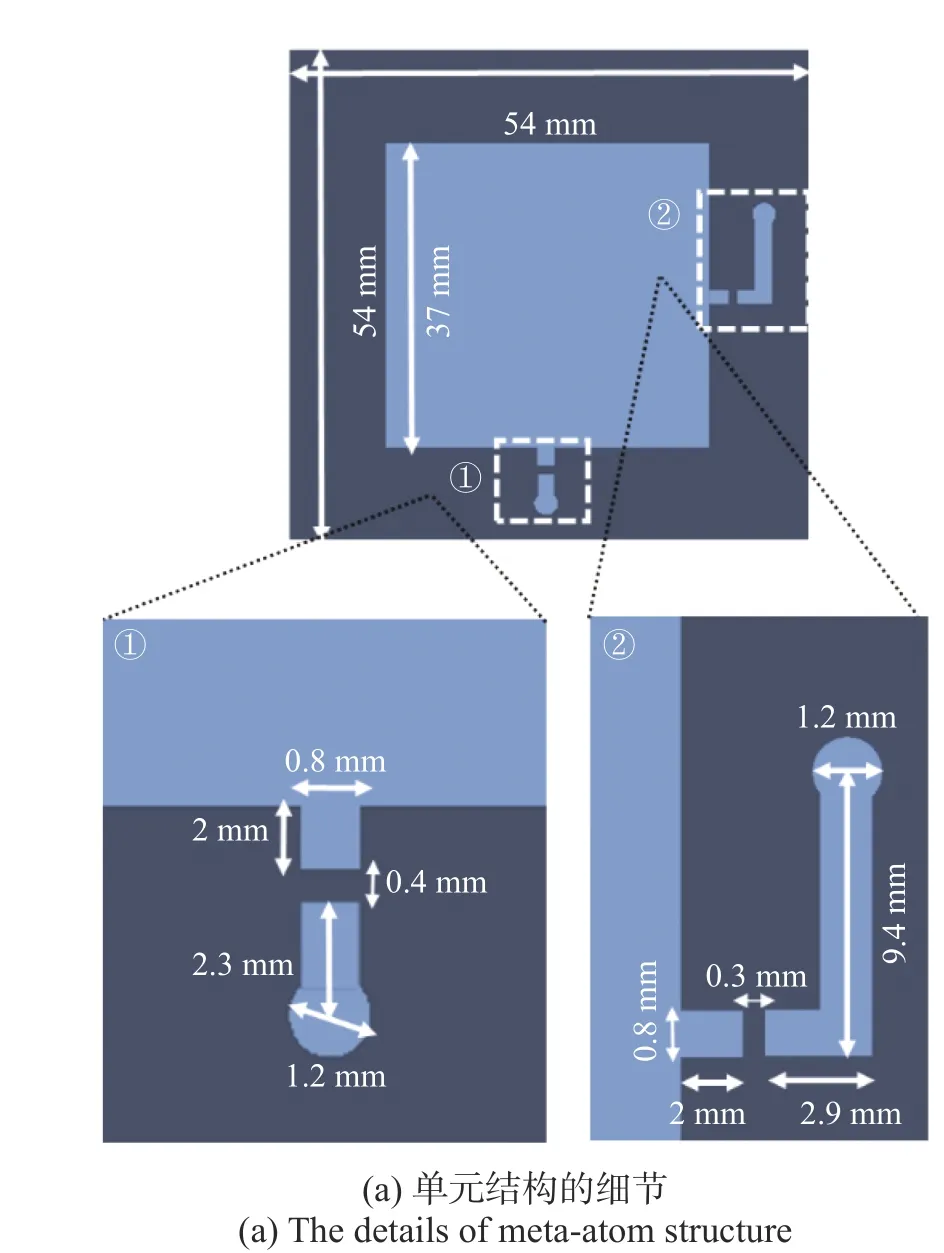
图5 可编程超表面及其性能测试Fig. 5 The programmable metasurface and its measurement

2.2 可编程超表面的散射场调控

本小节主要研究所制作的可编程超表面操纵电磁波的性能. 为此，本文首先提出了一个有效的预测模型来快速计算可编程超表面的散射场. 不失一般性，假设可编程超表面由N×M个单元组成. 首先，利用最小二乘方法[4,18]计算超表面单元的等效电流，并将其排列成列向量JS：

式中：S表示超表面单元的开关状态；A是传输矩阵，其元素来自于自由空间中并矢格林函数； γ表示人工正则化参数；I是对角矩阵；Ee是列向量，表示单个超表面单元在距离其半波长处的散射场，具体数值由CST 仿真得到. 一旦计算得到不同状态下单元的等效电流，根据叠加原理可以很容易地计算出不同编码序列对应的大口径可编程超表面的散射场：

图6 提供了一组不同编码序列对应的仿真结果，并且比较了预测模型与CST 仿真结果的差异. 第一行表示不同的编码序列，第二行和第三行分别表示由预测模型和商业软件CST 计算得到的仿真结果. 显然，该预测模型能够达到与商用软件几乎一致的性能，且二者之间的均方误差(mean square error,MSE)为0.011，但预测模型的计算时间仅为CST 的十分之一.

图6 可编程超表面预测模型与商业软件CST 计算得到的散射场比较Fig. 6 Comparison of radiation field distributions of the metasurface between our prediction model and CST

在预测模型的基础上利用Gerchberg-Saxton 算法快速设计可编程超表面的编码序列[18]. 图7(a)给出了本文调控可编程超表面的散射场为矩形形状的仿真和测量结果，其中红色虚线区域为仿真与实际测量的对比区域，可编程超表面散射场所形成的矩形区域的物理面积为124.2 cm×59.4 cm. 测量结果由图7(b)所示的近场扫描测量装置获得，其中的子图给出了优化后的可编程超表面对应的编码序列. 图7表明利用可编程超表面可以任意操纵电磁波的波前.

图7 矩形状的超表面散射场的仿真与测量结果及扫描测量装置Fig. 7 Comparison between the predicted radiated fields and the measured results; the experimental setup of near-field scanning

上述结果表明本文研制的1 比特反射型可编程超表面在电磁物理调控方面具有强大的能力，为后续构建低成本、高效率的智能感知系统奠定了基础.

3 深度学习驱动的智能感知实验

本节将深度学习引入电磁感知系统的数据处理层，在现实环境中实现智能成像.

3.1 智能感知实验装置

基于可编程超表面的智能感知系统的实验装置如图8 所示. 矢量网络分析仪(vector network analyzer,VNA)Agilent E5071C 两个端口分别与两个喇叭天线连接，用于发射微波信号和接收被测目标散射的回波信号. 其中一个天线作为发射天线以20°的倾斜角照射可编程超表面，发射天线与超表面之间的距离可以根据文献[31]的方法优化，以获得最佳的口径效率. 另一个天线作为接收天线用于接收位于可编程超表面3 m 处人体目标的散射波. 主控计算机通过基于FPGA 的控制板向可编程超表面发送控制编码序列，用来调控其照明目标的散射场模式. 同时，主控计算机控制VNA 记录目标在频段2.3～2.5 GHz内101 个采样频点处的S12参数.

图8 智能电磁感知实验测量装置Fig. 8 The measurement setup of sensing system

为了增强测量得到的目标信息容量，对于相同的目标需要进行多次不同照明模式的测量. 可编程超表面利用63 组杂乱无序的照明模式对被测目标进行测量，如图9(a)所示，杂乱无序的辐射模式可以看作由许多不同辐射方向的平面波线性组合. 通过这样的方式，可编程超表面可以捕获被测目标位于不同角域的空间信息. 图9(b)给出了几种可编程超表面的随机照明模式的仿真结果，它们之间的相关性非常低，仅为0.018.

图9 可编程超表面在xoy 平面的电场照明模式及其仿真结果Fig. 9 Electric field illumination pattern of programmable metasurface at xoy plane and its simulation result

本文考虑了在真实的办公室场景中实现人体成像的感知任务. 图10 展示了可编程超表面系统测量得到的被测目标在不同人体姿势和不同时刻测量的若干实验原始数据，每个子图中的不同曲线表示相同人体姿势在不同时刻的测量数据. 很明显，在不同时刻观察到的相同姿势的测量数据表现出非常高的相似性，然而不同姿势之间的差别非常显著. 原始数据表明，基于可编程超表面的电磁感知测量系统对观测噪声和测量误差具有很强的鲁棒性.

图10 固定照明模式下在不同时刻测量的不同人体姿势的若干实验原始数据Fig. 10 Several experimental raw data for different human postures measured at various moments in fixed illumination pattern

3.2 数据驱动的深度学习模型

将不同照明模式下的测量数据变形为矩阵形式后，利用深度学习技术对其进行数据处理，完成成像任务. 众所周知，深度学习是一种数据驱动的强大技术，非常适用于处理复杂环境中的逆散射问题. 图11给出了本文用于成像的卷积神经网络模型，该模型主要包括结构相似的卷积和反卷积过程. 以卷积过程为例，其主要由三个变形的残差神经网络模块和两个卷积层组成. 在每个模块中，采用两个独立的并行分支来避免梯度消失和爆炸，其中一个分支由单卷积层组成，另一个分支由两个卷积层组成. 反卷积过程具有相似的结构，除了两个残差神经网络模块位于反卷积层两侧. 上述所有模块均采用批量归一化(batch normalization, BN)层和Softplus 非线性激活函数. 具体的神经网络参数已经在图11 中详细标出.例如，“k5n64s2”表示卷积核的大小为5×5，特征数为64，步长为2. 最后，所设计的卷积神经网络模型实现了从101×63 的微波数据到128×128 的重建图像的端到端映射.

图11 卷积神经网络模型Fig. 11 The complete architecture of the proposed deep-learning-driven data processing model

本文利用采集的实验数据集对上述提出的卷积神经网络模型进行训练和测试. 有标记的训练样本来自于一台400 万像素的商用数码光学相机，拍摄到的物理面积为2 m×1.5 m. 在对光学图像进行背景去除、阈值饱和、二值化等预处理后，将其作为微波数据的标签. 上述操作的目的是消除背景环境的干扰. 最后，利用基于可编程超表面的感知系统在普通办公环境中采集了8 000 对有标签的训练样本，总计包括20 多种显著变化的人体姿势. 其中，数据集的80%通过自适应矩估计(adaptive moment estimation,ADAM)优化器用于模型训练，设置批量大小为32，迭代周期为101，剩余的20%用于测试. 本文的深度学习模型是在TensorFlow 框架下设计的，在配备Intel Xeon E5-1620v2 中央处理器、NVIDIA GeForce GTX 1080Ti 和128 GB 访问内存的工作站上进行训练.

3.3 电磁感知性能分析

图12 给出了多组成像结果，可以看出，基于深度学习的智能感知方法具有优越的成像性能. 第一行和第二行为被测人体姿态的真实光学图像，第三行和第四行为由基于可编程超表面的感知系统测量得到的微波数据矩阵，第五至第六行为经过卷积神经网络重建的人体姿态. 不难看出，重构后的人体姿态图像轮廓清晰，与真实光学图像相比具有很高的保真度. 本文利用相似结构指数(structural similarity, SSIM)和MSE 对成像质量进行定量分析，得到SSIM 和MSE 分别为0.75 和0.027 5. 上述实验仅对被测目标进行了63 次测量，测量次数远远低于重构场景包含的128×128 个像素数目，即基于深度学习驱动的可编程超表面智能感知系统以16 384:63的极高压缩比实现了高质量的人体姿态成像.

图12 深度学习驱动智能感知实验结果Fig. 12 Some selected test results for the deep-learning-driven sensing scheme

如前文所述，当成像目标无限接近可编程超表面时，电磁感知系统自身可提供的最小分辨率为λmin/2. 当工作频率为2.43 GHz 时，横向分辨率的衍射极限为6.17 cm，远大于本文被测场景的像素1.56 cm×1.17 cm. 上述结果表明，将深度学习技术引入电磁感知系统的数字处理层可以有效解决非线性电磁逆散射问题，使基于可编程超表面电磁感知系统具有更优越的性能.

4 结 论

本文从理论、系统和实验的角度出发研究了一种深度学习与可编程超表面协同工作的智能感知方法. 首先利用“k 空间”法分析了没有使用高级数据后处理算法时，基于可编程超表面的电磁感知系统自身提供的成像分辨率和影响分辨率的关键因素.然后，制造和测试了一款反射型可编程超表面，并研究其在电磁物理层面调控电磁波波前的性能. 基于该可编程超表面，本文将深度学习引入电磁感知系统的数据处理层，在真实环境中以极少的测量次数实现了高保真度的人体姿态成像，其研究结果可以指导未来人工智能时代的电磁智能感知系统的设计与分析.