基于大比例尺DLG的电子地图道路面快速构建方法研究
吴国华
(福州市勘测院,福建 福州 350108)
1 引 言
随着信息技术的快速发展和人们对电子地图应用需求的不断提高,电子地图产品已经融入人们日常生活和工作的每一个角落。在当今城市建设快速发展的环境下,城市地表各类地物的信息变化可谓日新月异,采用何种方式、何种频率对电子地图进行常态化生产更新,使其时刻保持其数据现势性成为测绘地理信息行业应用研究人员面前的当务之急[1]。电子地图的更新方法通常是采用大比例尺DLG数据进行生产加工,而道路作为电子地图的关键要素,在电子地图的生产中占有至关重要的地位。传统的道路网构建处理方式是通过人工闭合道路边线分段构建道路面,其作业工作量大且效率低,很难满足当前市场对电子地图快速更新的需求。本文结合福州市全市域1.2万平方千米范围电子地图生产需求,以FME为基础平台,通过对福州市全市域 1∶2 000 DLG道路边线进行分区自动构建道路面的方法,可以快速完成道路面的生产和更新工作。
2 数据现状
福州市已经建成覆盖全市域1.2万平方千米的 1∶2 000 DLG数据库,是电子地图生产和更新的基础数据来源。1∶2 000 DLG数据库中居民地、水系、绿地等图层数据是已经拓扑构建的面图层数据,关键地物要素仅有交通层是以矢量线图层存储的数据。因此以道路边线进行电子地图中道路面的构建,成为电子地图生产与更新的主要工作内容。通过对 1∶2 000 DLG数据库中交通相关图层数据提取分析,其数据内容包含交通线层、交通注记层共两大类型。其中交通线图层总计包含166类地物编码的各类交通线,其属性内容包含属性ID、地物编码、采集时间、长度等字段。但交通线层多为细碎的矢量线段、且在与居民地等其他地物要素连接处为非闭合状态。如采用人工拓扑进行断线连接、拓扑构面的方式,作业进度缓慢,将耗费大量的人力。
3 道路面构建
3.1 作业原理
3.1.1 构建Delaunay三角网
Delaunay三角网是一系列相连的但不重叠的三角形的集合[2]。空外接圆性质和最大最小角性质是Delaunay三角网具有的两个特有的性质。其中最大最小角性质是指:Delaunay三角网最大化最小角特性在散点集可能形成的三角剖分中,Delaunay三角剖分所形成的三角形的最小角最大[3]。其在现代地理科学与计算机科学中的表现和应用中,可以理解为两个相邻的三角形构成凸四边形的对角线,在相互交换后,六个内角的最小角不再增大的几何特性。针对这一几何特性来讲,Delaunay三角网是“最接近于规则化的”的三角网。其最大最小角性质构建三角形的构建方式具体如图1所示:
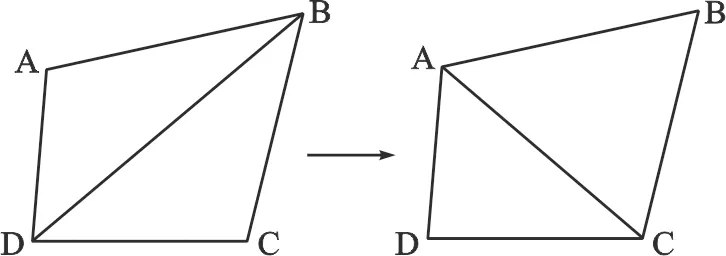
图1 Delaunay三角网最大最小角性质说明示意图
Delaunay三角网的优点是结构良好,数据结构简单,数据冗余度小,存储效率高,与不规则的地面特征和谐一致,可以表示线性特征和叠加任意形状的区域边界,易于更新,可适应各种分布密度的数据等[4]。正是本身的这些优点,决定了它在现代地理科学与计算机科学中的不可忽视的地位,常被应用于GIS中的网络分析中,成为描述地表形态的一种公认方法,是地表(地貌和地物)数字化表现的重要手段和常用分析工具。
根据Delaunay三角网最大化最小角特性,以待构建道路边线节点集作为Delaunay三角网构建数据源,通过对道路边线节点集形成最小的封闭凸壳,将封闭壳体范围内的几何对象分解成一系列相连但不重叠的三角形单元网格,从而以道路边线节点集构建成覆盖道路边线内部区域范围的Delaunay三角网。简而言之就是采用Delaunay三角网来数字化表现道路的一种GIS表现方式。
3.1.2 区分非法Delaunay三角形
在以道路边线的节点集为数据源构建Delaunay三角网的过程中,如果道路边线的节点集范围中包含非凸区域或者存在内环,则会产生非法三角形[5~7]。此处表现在图上就是构建在道路边线范围以外的Delaunay三角形。如图2所示的红色三角形即为非法三角形,从图中可以看出非法三角形一般形成在道路边线相交处的夹角位置和环形道路边线内,即节点集的非凸区域和存在内环的位置。而此类非法的三角形是道路面构建中的冗余数据,需要从构建的三角网中区分出来并剔除掉,以免干扰后继的道路面构建。

图2 非凸区域或者存在内环时产生的非法三角形示意图
在现代地理科学与计算机科学中,矢量又称为向量,是指既有大小又有方向的量。矢量数据是计算机中以矢量结构存贮的内部数据,它是跟踪式数字化仪的直接产物。在矢量数据结构中,矢量点数据可直接用其坐标值表示;矢量线数据可用均匀或不均匀间隔的顺序坐标链来表示;矢量面状数据(或多边形数据)可用边界线来表示[8]。这样,用点、线、多边形构成的图形统称为矢量图。根据Delaunay三角网构建的方式及矢量数据的方向特性,通过非凸区域或者存在内环时产生的三角形与其他区域构建形成的三角形存在不同的矢量方向的原理,从而完成非法三角形的区分归类[9]。具体区分归类数据表示形式如图2中红色矢量线表示的三角形为非法三角形。
3.1.3 创建拓扑三角形区域
在现代地理科学与计算机科学中GIS数据通过Point、Polyline、Polygon来表达地物的点、线、面要素。在GIS坐标系中Point(点)用一个坐标对(x、y)或(x、y、x)来表示;Polyline(线)作为点之间的连线,用一系列坐标对来表达线的转折位置,在程序中依据点连接成线;Polygon(多边形区域)与Polyline(线)的区别是Polygon(多边形区域)是首尾相连的Polyline(线),因此与Polyline(线)的表达方式相同,也用一系列转折位置的坐标表示,同时,其最后一个坐标Point(点)与首Point(点)坐标相同。基于这一表达方式,把构建的Delaunay三角网中的每一个三角形都可以认为是首尾相连的Polyline(线)[10],从而经过拓扑处理可以构建成一系列无缝拼接的Polygon(三角形区域)。
3.1.4邻接面融合
在构建的一系列无缝拼接的Delaunay三角网面中,相邻接的两个三角形面都有一个公共边界线,可以通过删除相邻接三角形公共边界线来融合两个三角形面要素,从而创建一个更大的合并四边形面区域。利用同样的方式对相邻接的两个四边形面进行融合成更大的多边形面区域,直至所有相邻接的Delaunay三角形面融合成一个完整的区域。
3.2 应用实践
3.2.1 作业流程(图3)
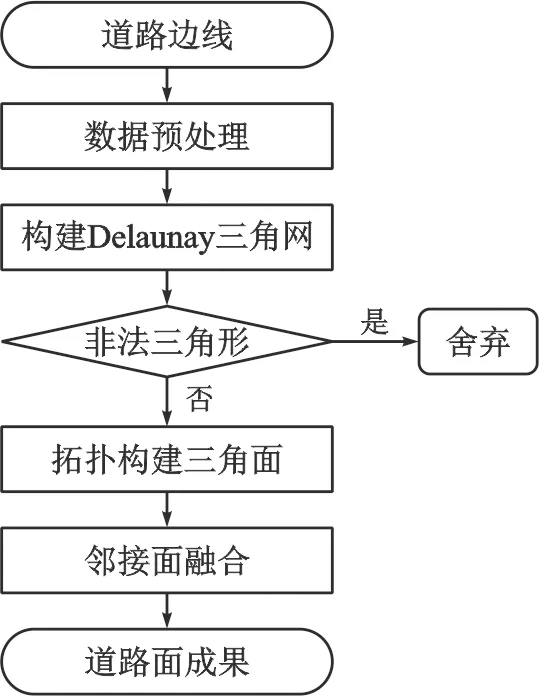
图3 道路面构建流程图
作业源数据为已有福州市1∶2 000比例尺DLG交通层数据。
第一步需要对源数据进行数据预处理,即进行冗余筛除、干扰数据清除、数据分类、断线连接、去除毛刺等预处理操作。
第二步在预处理的数据基础上,通过FME平台相关转换器构建数据外壳对道路边线节点集构建Delaunay三角网。
第三步根据Delaunay三角网构建的方式及矢量数据的方向特性判断区分非法三角形。
第四步对剔除非法三角形后的Delaunay三角网通过闭合线拓扑构建三角面网。
第五步对相邻接的拓扑面数据进行融合最终形成覆盖道路边线范围的道路面数据成果。
3.2.2 数据预处理
对待处理的交通线数据进行冗余筛除、干扰数据清除、数据分类、断线连接、去除毛刺等数据预处理工作主要处理内容如下:
(1)冗余筛除:筛除交通线数据中不需要构建道路面的交通线类数据,主要筛除内容包括一般铁路、地下铁路、城市轻轨、电车轨道、缆车轨道、架空索道、站台、站台雨棚、天桥的阶梯、地道的地表出入口及其他交通附属设施线类。
(2)干扰数据清除:需要手工清除独立于整个交通路网以外且细碎不完整的交通线,这些交通线因远离交通路网且细碎不完整在数据构建时不能构成三角网,且会干扰其他正常道路边线构建三角网。
(3)数据分类:根据道路等级编码和类型对交通线数据进行分类,筛选出郊区道路(大车路、小路)、城市道路(城区主次干道及街巷)、复杂道路(高架、立交桥)等进行数据分类。
(4)断线连接:大比例尺DLG数字线划图中因为地物要素的表达关系等原因,整条道路边线是有多个多段线组成,不少多段线间还存在一定的间隙。为了提高数据处理的质量,需要对相邻的断线进行连接预处理。此处借助FME的LineCombiner、Snapper转换器,通过设置从小到大的连接参数值,进行循环连接断开的道路边线。具体的FME循环连接处理流程图部分截图如图4所示。

图4 FME中循环连接处理道路边线的流程图
(5)去除毛刺:道路边线中在不同道路连接处及道路与其他地物要素衔接处不可避免地会有凸起的锐角毛刺现象,如图5所示。这种毛刺现象严重干扰道路面构建的效果,利用FME的SpikeRemover转换器,通过角度设定参数自动消除掉道路边线中的毛刺修复平滑道路边线。

图5 道路边线中的毛刺示意图
如图6、图7是通过数据预处理后的城区道路边线效果对比图。
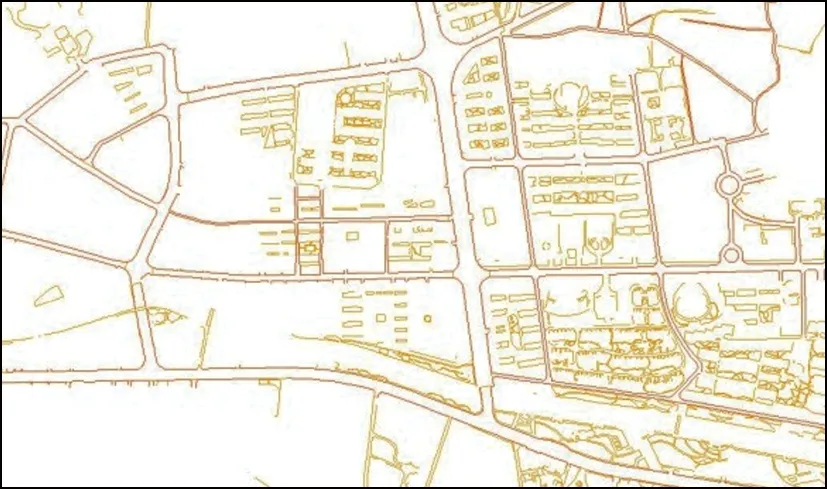
图6 预处理前的城区道路边线
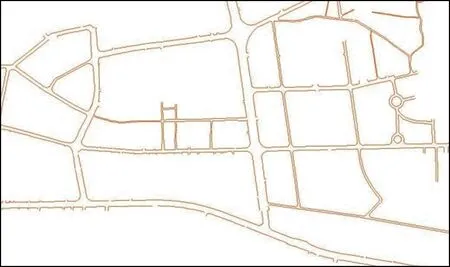
图7 预处理后的城区道路边线
3.2.3 基于道路边线构建Delaunay三角网
根据Delaunay三角网最大化最小角特性,以待构建道路边线节点集作为Delaunay三角网构建中各个三角形的顶点,利用FME平台的Hullaccumulator、Triangulator、Deaggregator转换器,对道路边线节点通过形成封闭外壳,将封闭壳体范围内的几何对象分解成三角形单元网格。
构建Delaunay三角网的转换器函数与alpha初始值的设置,需要参照预处理过程中道路等级及道路宽度的分类类型。设置alpha初始值一般与待处理道路宽度相近时构建的效果最佳,因此对道路宽度分类合理与否对构建效果有着直接的影响。组合转换器通过Delaunay三角网内的各个Delaunay三角形的外接圆半径r进行计算,舍弃外接圆半径r值超过设定初始值alpha的Delaunay三角形,并对组合的网格以单一的三角形为最小单元打散,从而以道路边线节点构建成覆盖道路区域范围的Delaunay三角网。如图8是应用FMEWorkbench进行道路边线范围的Delaunay三角网构建流程图,图9是由城区道路边线生成的覆盖道路边线范围的Delaunay三角网效果图。

图8 应用FMEWorkbench进行道路边线范围的Delaunay三角网构建流程图

图9 由城区道路边线生成的覆盖道路边线范围的Delaunay三角网效果图
3.2.4 区分剔除非法Delaunay三角形
在以道路边线的节点集基于FME平台的Hullaccumulator、Triangulator转换器来构建Delaunay三角网的方法实际应用当中,如果道路边线的节点集范围中包含非凸区域或者存在内环,则会产生非法三角形,此处表现在图上就是构建在道路边线范围以外的三角形。具体如图10和图11(局部放大图)所示的红色三角形即为非法三角形,从图中可以看出非法三角形一般形成在道路边线相交处和道路边线内环处。而此类非法的三角形是道路面构建中的冗余数据,需要剔除掉,以免在后期的构面处理中误构成道路面。

图10 Delaunay三角网中非法三角形(红色)区分示意图

图11 Delaunay三角网中非法三角形(红色)局部放大示意图
根据Delaunay三角网构建的原理及矢量数据的方向特性,通过非凸区域或者存在内环时产生的三角形与其他区域的三角形方向不同的矢量属性来区分非法三角形。使用FME的OrientationExtractor转换器把Delaunay三角形隐藏的矢量方向属性暴露出来。然后根据FME中tester转换器对输入要素执行测试条件,从而将点集范围是非凸区域或者存在内环的矢量方向不一致的三角形(非法三角形)区分归类并剔除掉。具体区分剔除非法Delaunay三角形的处理流程图如图12所示。

图12 区分剔除非法Delaunay三角形的处理流程图
3.2.5 拓扑构建三角面
在3.2.3基于道路边线构建三角网和3.2.4区分剔除非法Delaunay三角形的基础上,利用FME的LineOnLineOverlayer转换器,对道路边线范围内三角网中的各个三角形的多段线进行拓扑处理以获取一系列拓扑关系上连接的闭合三角形多段线,然后利用FME的AreaBuilder转换器对形成首尾闭合的多段线创建拓扑正确的三角形面要素,即形成一系列无缝拼接的不规则三角面道路网。具体处理流程图如图13所示。

图13 Delaunay三角网拓扑构面及邻接面融合生成道路面流程图
3.2.6 邻接面融合生成道路面
基于生成的一系列无缝拼接的不规则三角面道路网,应用FME的Dissolver转换器,通过删除相邻接三角形公共边界来融合面要素的功能,从而创建更大的合并区域。采用此种方式对由Delaunay三角网拓扑构建的一系列无缝邻接的不规则三角面网进行相邻面融合合并,最终将Delaunay三角形要素面融合成完整的道路面。具体处理流程图如图13。融合后的城区道路和郊区山路的道路构面效果图如图14和图15所示。
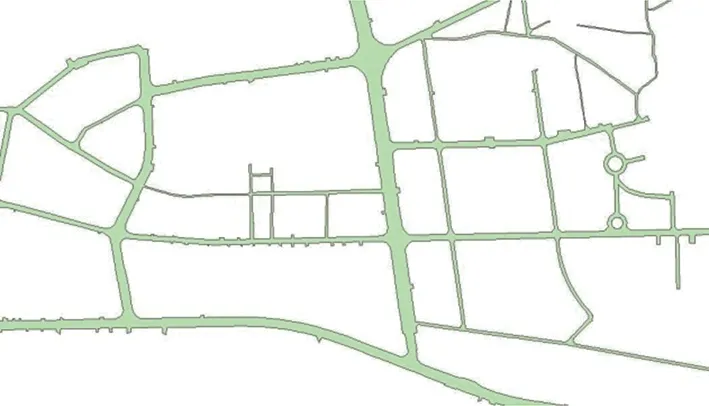
图14 城区道路面融合效果图

图15 郊区山路道路面融合效果图
4 总 结
通常道路面构建方法有人工边线连接分段构建法和道路中心线缓冲构面法两种方法。第一种方法需要投入大量的人工进行断线连接、分段拓扑构面等,工作量十分庞大且作业效率低下;第二种方法需要根据道路边线采用人工绘制道路中心线、并量取道路宽度值,然后再通过缓冲构面,虽然效率有所提升但是存在道路交叉处的喇叭口处衔接十分生硬及与道路宽窄变化的体现严重不足等问题。
相比传统方法的道路构面不足的情况,本文基于大比例尺DLG的电子地图道路面快速构建方法优势十分明显,不仅有传统人工边线连接构建道路面的美观效果,而且构建效率有了十分显著的提高。在福州市全市域电子地图生产更新项目建设中,为电子地图的道路面快速生产及更新提供了一套切实有效的解决方法。

